Производные сложных функций Найти производную функции:

768.00K

Категория: $Математика$ Математика

Похожие презентации:

Производная функции. Определение производной

Производная и дифференциал. Лекция 5

Производная функции

Производная. Определение производной

Производная функции

Производная функции. Лекция 4

Производная функции

Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал

Производная функции. Лекция 2

Производная функции. Правила дифференцирования. Основные свойства дифференцируемых функций. Производные элементарных функций

Производная функции. Определение производной

1. Лекция Производная функции.

План лекции:
1.Определение производной. Геометрический и
механический смысл производной.
2. Нахождение производных.
Схема нахождения производной. Правила
дифференцирования.
Производная
сложной
функции.
3. Производные элементарных функций.
(Производная
логарифмической
функции,
производная
показательной
функции,
производная степенной функции, производная
тригонометрических функций).
19 февраля 2024 г.
4. Примеры нахождения производных.

2. 1. Производная

Определение
Геометрический смысл
Механический смысл
19 февраля 2024 г.

3. 1.Определение производной

Производной функции y = f (x) называется предел отношения
приращения функции к приращению аргумента при стремлении
последнего к нулю:
y
y lim
x 0
x
y
f (x+ x)
y=f (x)
y
f (x)
x
0
Иванов О.В., Кудряшова Л.В., 2005
x
x+ x
x
3

4. Лагранж Жозеф Луи

Лагранж
Жозеф
Луи
(1736-1813)
–
французский математик и механик, член
Берлинской и Парижской Академии наук.
Самостоятельной изучал математику, в 23 года
стал академиком. Сделал массу открытий.
Парижская АН пять раз присуждала ему
премии. В математике и механике его именем
названы несколько методов, формул и теорем.
Термин «производная» введен Лагранжем на
рубеже
18-19
веков.
Производная
–
произведенная, полученная по определенным
правилам из данной функции.
Иванов О.В., Кудряшова Л.В., 2005
4

5. Дифференцируемая функция

Нахождение производной называется дифференцированием
этой функции.
Если функция в точке x имеет конечную производную, то
функцию называют дифференцируемой в этой точке.
Функция, дифференцируемая во всех точках промежутка X,
называется дифференцируемой на этом промежутке.
Иванов О.В., Кудряшова Л.В., 2005
5

6. Четыре обозначения для производной

y
dy
dx
y
Dy
Лагранжа (читается «игрек штрих»)
Лейбница (читается «дэ игрек по дэ икс»)
Ньютона (читается «игрек с точкой»)
Коши (читается «дэ игрек»)
Иванов О.В., Кудряшова Л.В., 2005
6

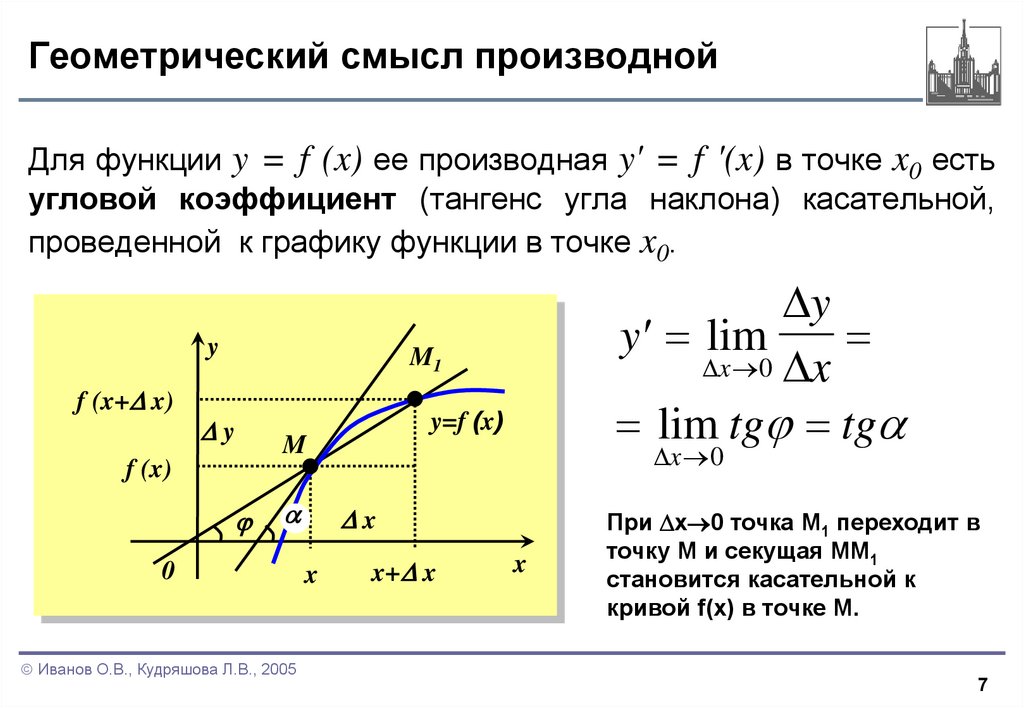
7. Геометрический смысл производной

Для функции y = f (x) ее производная y' = f '(x) в точке x0 есть
угловой коэффициент (тангенс угла наклона) касательной,
проведенной к графику функции в точке x0.
y
f (x+ x)
y
y lim
x 0 x
lim tg tg
M1
y
y=f (x)
M
x 0
f (x)
0
Иванов О.В., Кудряшова Л.В., 2005
x
x
x+ x
x
При x 0 точка M1 переходит в
точку M и секущая MM1
становится касательной к
кривой f(x) в точке M.
7

8. Механический смысл производной

Для функции y = f (x), меняющейся со временем x, производная
y' = f '(x) есть скорость изменения y в момент x0.
Пройденный путь s зависит от времени t: s = s(t).
Скорость:
s
st lim
v( t )
t 0 t
Ускорение:
v
v t lim
w (t )
t 0 t
Иванов О.В., Кудряшова Л.В., 2005
8

9. Лейбниц Готфрид Вильгельм

Лейбниц Готфрид Вильгельм (1646-1716) –
немецкий философ, математик, физик,
изобретатель, юрист, историк, экономист,
дипломат, языковед, член Лондонского
королевского общества и Парижской
Академии наук, основатель Берлинской
Академии наук.
В
18
лет
защитил
магистерскую
диссертацию по философии, в 20 лет стал
доктором права.
Является
одним
из
создателей
математического
анализа,
алгебры
определителей,
дифференциального
и
интегрального исчислений.
Иванов О.В., Кудряшова Л.В., 2005
9

10. Ньютон Исаак

Ньютон
Исаак
(1643-1727)
–
английский физик и математик, член
Лондонского королевского общества (с
1672) и его президент (с 1703).
Им
начато
построение
математического анализа на основе
учения о пределе, подготовлены
основы для дифференциального и
интегрального исчисления. В физике
обосновал справедливость закона
всемирного
тяготения,
законы
движения, теорию света и др.
Иванов О.В., Кудряшова Л.В., 2005
10

11. Непрерывность и дифференцируемость

Теорема. Если функция дифференцируема в некоторой точке
x Df, то в этой точке функция непрерывна.
Доказательство. Если существует производная, тогда
y
lim y lim x
x 0
x 0 x
y
lim lim x y 0 0
x 0 x x 0
Это означает, что функция в этой точке непрерывна. Обратное
утверждение неверно.
Иванов О.В., Кудряшова Л.В., 2005
11

12. 2. Нахождение производных

Схема нахождения производной
Правила дифференцирования
Производная сложной и обратной функций
Производная неявной функции
19 февраля 2024 г.

13. Нахождение производной по определению

1. Для фиксированного значения x аргумента
находится исходное значение функции y = f (x).
функции
2. Аргументу x дается приращение x и находится новое
значение функции f (x + x).
3. Вычисляется приращение функции y = f (x + x) – f (x).
4. Находится предел отношения:
y
lim
y ( x )
x 0 x
Иванов О.В., Кудряшова Л.В., 2005
13

14. Производная постоянной

Функция:
y C
1. Для фиксированного значения x аргумента функции находим
исходное значение функции y = f (x) = C.
2. Аргументу x даем приращение x и находим новое значение
функции f (x + x)= C.
3. Вычисляем приращение функции:
y = f (x + x) – f (x) = C – C = 0.
4. Находим предел отношения:
y
0
C lim
lim
0
x 0 x
x 0 x
Иванов О.В., Кудряшова Л.В., 2005
14

15. Производная x2

Функция:
y x
2
1. Для фиксированного значения x аргумента функции находим
исходное значение функции y = f (x) = x2.
2. Аргументу x даем приращение x и находим новое значение
функции f (x + x)= (x + x)2.
3. Вычисляем приращение функции:
y = f (x + x) – f (x) = x2 + 2x x + x2 – x2.
4. Находим предел отношения:
y
2 x x x
C lim
lim
2 x x 2 x
x 0 x
x 0
x
2
Иванов О.В., Кудряшова Л.В., 2005
15

16. Производная суммы

Производная суммы двух дифференцируемых функций равна
сумме производных:
(u v ) u v
Доказательство.
u( x x ) v ( x x ) (u( x ) v ( x ))
(u( x ) v ( x )) lim
x 0
x
u( x x ) u( x ) v ( x x ) v ( x )
lim
x 0
x
x
u
v
lim
lim
u ( x ) v ( x )
x 0 x
x 0 x
Иванов О.В., Кудряшова Л.В., 2005
16

17. Производная произведения

Производная произведения двух дифференцируемых функций
находится по формуле:
(uv ) u v uv
Доказательство.
u( x x ) v ( x x ) u( x ) v ( x )
(u( x ) v ( x )) lim
x 0
x
u u
v
lim u
v
v uv vu u lim v
x 0 x
x 0
x x
u v uv
Иванов О.В., Кудряшова Л.В., 2005
17

18. Производная частного

Производная частного
находится по формуле:
двух
дифференцируемых
функций
u v uv
u
2
v
v
Доказательство. Самостоятельно.
Иванов О.В., Кудряшова Л.В., 2005
18

19. Производная сложной функции

Если y есть дифференцируемая функция от u, а u есть
дифференцируемая функция от x, то производная сложной
функции существует и равна производной внешней функции,
умноженной на производную внутренней функции:
y x yu (u) ux ( x )
Доказательство.
y
y u
y
u
yx lim
lim
lim
lim
yu ux
x 0 x
x 0 u x
u 0 u x 0 x
u 0
Иванов О.В., Кудряшова Л.В., 2005
19

20. 3. Производные элементарных функций

Производные логарифмической функции
Производная показательной функции
Производная степенной функции
Производные тригонометрических функций
Таблица производных
19 февраля 2024 г.

21. Производная логарифмической функции

Функция:
y ln x
Производная:
1
y (ln x )
x
Доказательство.
1. Для фиксированного значения x аргумента функции находим
исходное значение функции:
f ( x ) ln x
2. Аргументу x даем приращение x и находим новое значение
функции:
f ( x x ) ln( x x )
Иванов О.В., Кудряшова Л.В., 2005
21

22. Производная логарифмической функции

3. Вычисляем приращение функции:
y f ( x x ) f ( x ) ln( x x ) ln( x )
x x
x
ln
ln 1
x
x
4. Находим предел отношения:
y
1 x
y lim
lim
ln 1
x 0 x
x 0 x
x
1 x x
lim
ln 1
x 0 x
x
x
Иванов О.В., Кудряшова Л.В., 2005
x
x
1
1
ln e
x
x
22

23. Производная логарифмической функции

Функция:
y log a x
Производная:
1
y (log a x )
x ln a
Доказательство: самостоятельно
Иванов О.В., Кудряшова Л.В., 2005
23

24. Производная показательной функции

Функция:
y e
Производная:
y (e ) e
x
x
x
Доказательство.
Обратная функция: x ln y
Находим, как производную обратной функции:
1
y x
x y
1
1
1
x
y x (e )
y e
x y (ln y ) y 1
y
x
Иванов О.В., Кудряшова Л.В., 2005
24

25. Производная показательной функции

Функция:
y a
Производная:
y (a ) a ln a
x
x
x
Доказательство. Самостоятельно.
Иванов О.В., Кудряшова Л.В., 2005
25

26. Производная степенной функции

Функция:
Производная:
y x
n
y n x
n 1
Доказательство.
Логарифмируем обе части равенства
Дифференцируем: 1
1
y
ln y n ln x
y n
x
1
1
n
n 1
y y n x n n x
x
x
Иванов О.В., Кудряшова Л.В., 2005
26

27. Производные тригонометрических функций

Функция:
y sin x
Производная:
y cos x
Доказательство.
y
sin( x x ) sin x
y lim
lim
x 0 x
x 0
x
x
x
x
2 sin
cos x
sin
x
2
2
2
lim
lim
lim cos x cos x
x x 0
x 0
x 0
x
2
2
Иванов О.В., Кудряшова Л.В., 2005
27

28. Производные тригонометрических функций

Функция:
y cos x
Производная:
y sin x
Функция:
Производная:
y tg x
1
y
cos2 x
Доказательство. Самостоятельно.
Иванов О.В., Кудряшова Л.В., 2005
28

29. Таблица производных

Иванов О.В., Кудряшова Л.В., 2005
29

30.

Найдите производные функций:
1
а) f ( x) x
х
2
б ) f ( x ) x ( 2 x 7)
2
2
x
в) f ( x) 3
x 1
Иванов О.В., Кудряшова Л.В., 2005
г) f ( x) x
5
5
д) f ( x ) 3 x 3
x
7
30

31.

1
а) f ( x) x
х
1
1
2
2
f ( x ) ( x ) ( x ) ( )
х
х
2
1
1
2 x ( 2 ) 2 x 2
х
х
Иванов О.В., Кудряшова Л.В., 2005
31

32.

б ) f ( x ) x ( 2 x 7)
2
f ( x ) ( x ) ( 2 x 7) ( х ) ( 2 х 7)
2
2
2 x ( 2 x 7) х 2 4 x 14 х 2 х
2
2
2
6 x 14 х
2
Иванов О.В., Кудряшова Л.В., 2005
32

33.

2
x
в) f ( x) 3
x 1
2
3
2
3
( x ) ( х 1) х ( х 1)
f ( x )
3
2
( x 1)
4
4
2 x ( х 1) х 3 х
2
х
2
х
3
х
3
2
3
2
( x 1)
( x 1)
3
2
2
х 2х
3
2
( x 1)
4
Иванов О.В., Кудряшова Л.В., 2005
33

34.

г) f ( x) x
5
f ( x ) ( x ) 5 x
5
Иванов О.В., Кудряшова Л.В., 2005
5 1
5x
6
34

35.

5
д) f ( x ) 3 x 3
x
5
7
3
7
f ( x ) ( 3 x 3 ) ( 3 x ) (5 х )
x
7
3 7 x 5 ( 3 х
6
3 1
) 21 x 15 х
6
4
15
21 x 4
x
6
Иванов О.В., Кудряшова Л.В., 2005
35

36. Производные сложных функций Найти производную функции:

Иванов О.В., Кудряшова Л.В., 2005
36

37. Найти производную функции :

Иванов О.В., Кудряшова Л.В., 2005
37

38. Найти производные функций:

Иванов О.В., Кудряшова Л.В., 2005
38