Похожие презентации:
Элементы матанализа. Применение производной при исследовании функции
1. Элементы матанализа. Лекция 2
Лектор: Войтик ВиталийВикторович
2. Применение производной при исследовании функции
• Теорема о необходимых признакахвозрастания и убывания функции.
• 1. Если функция y=f(x) дифференцируема и
возрастает на интервале (a,b), то
производная этой функции не отрицательна
y’≥0 во всех точках данного интервала.
3. 2. Если функция y=f(x) дифференцируема и убывает на интервале (a,b), то производная этой функции не положительна y’≤0 во всех
точках данного интервала.Теорема о признаке возрастания и
убывания функции. Если производная
функции положительна на некотором
интервале, то функция возрастает на этом
интервале, наоборот если производная
отрицательна, то функция убывает на этом
интервале
4. Экстремумами функции называются её точки максимума и минимума. Производная дифференцируемой функции в точке экстремума равна
нулю.Порядок действий при
исследовании функции.
5. 1. Найти область определения функции, которая может быть конечной или бесконечной. 2.Найти производную функции и определить
имеются ли точки, вкоторых производная не существует.
3.Приравнять производную к нулю и
решить полученное уравнение
f (x) 0
Корни этого уравнения являются
стационарными точками функции
6. 4. Найти критические точки функции, как совокупность всех стационарных точек и точек в которых производная не существует и
отметить их на оси ОХ5.Определить знаки производных на
интервалах, на которые критические
точки делят область определения
функции.
6.По знаку производной найти
интервалы возрастания и убывания
функции.
7. 7. Найти точки экстремумов функции. Пример. Исследовать функцию 1. Область определения этой функции (-∞,∞) 2.Производная 3.
7. Найти точки экстремумов функции.Пример. Исследовать функцию
1 3
2
y x x
3
1. Область определения этой функции (-∞,∞)
2.Производная
1 3 2
y x x x 2 2 x
3
y 0 x 2 2 x
3. Корни x=0, x=2
4.Эти корни стационарные и критические
точки функции
8. 5.Определим знаки производных в интервалах (-∞,0),(0,2),(2,∞).Для этого достаточно найти знак производной в любой точке
интервала. На (-∞,0) >0,(0,2)<0, (2,∞)>0
6. На (-∞,0) функция возрастает
, на (0,2) функция убывает
на (2,∞) функция возрастает.
7.Точка х=0 точка максимума
точка х=2 точка минимума
9.
Интегральное исчисление.Первообразная функция.
Функция F(x) называется первообразной функцией
функции f(x) на отрезке [a, b], если в любой точке этого
отрезка верно равенство:
F (x) = f(x).
Надо отметить, что первообразных для одной
и той же функции может быть бесконечно много.
Они будут отличаться друг от друга на некоторое
постоянное число.
F1(x) = F2(x) + C.
10.
Неопределенный интеграл.Определение: Неопределенным интегралом
функции f(x) называется совокупность
первообразных функций, которые определены
соотношением:
F(x) + C.
Записывают: f ( x)dx F ( x) C;
11.
xe
x 1
C , 1
dx
1
x
dx e c
dx
x
x
ln x C
ax
C
ln a
1
cos 2 x dx tgx C
1
sin 2 x dx ctgx c
cos xdx Sinx C
sin xdx Cosx C
dx
1 x2
arctgx C
12.
Свойства:1. f ( x)dx ( F ( x) C ) f ( x);
2.d
f ( x)dx f ( x)dx;
3. dF ( x) F ( x) C;
4. (u v w)dx udx vdx wdx;
где u, v, w – некоторые функции от х.
5. C f ( x)dx C f ( x)dx;
Пример:
1 3
( x 2 sin x 1)dx x dx 2 sin xdx dx 3 x 2 cos x x C;
2
2
13.
Методы интегрированияА) Непосредственное интегрирование.
14.
Б) Способ подстановки (заменыпеременных).
Пример. Найти неопределенный интеграл
Сделаем замену t = sinx, dt = cosxdt.
2 3/ 2
2 3/ 2
1/ 2
t dt t dt 3 t C 3 sin x C.
sin x cos xdx .
15. В) Интегрирование по частям.
Способ основан на известной формуле производной произведения:(uv) = u v + v u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем:
d (uv) udv vdu , а в соответствии с приведенными
выше свойствами неопределенного интеграла:
uv udv vdu
или
udv uv vdu ;
16.
Пример.2x
2x
u
e
;
du
2
e
dx;
2x
2x
2x
e
cos
xdx
e
sin
x
sin
x
2
e
dx
dv cos xdx; v sin x
u e 2 x ; du 2e 2 x dx; 2 x
2x
2x
2x
e sin x 2 e cos x cos x 2e dx e sin x
dv sin xdx; v cos x;
2e 2 x cos x 4 cos xe2 x dx
Видно, что в результате повторного применения
интегрирования по частям функцию не удалось упростить
к табличному виду. Однако, последний полученный
интеграл ничем не отличается от исходного. Поэтому
перенесем его в левую часть равенства.
2x
e
e
cos
xdx
(sin
x
2
cos
x
)
C
.
5
2x
17.
2u
x
; dv sin xdx;
2
2
Пример. x sin xdx
x
cos x cos x 2 xdx
du 2 xdx; v cos x
u x; dv cos xdx;
2
2
x
cos
x
2
x
sin
x
sin
xdx
x
cos x 2 x sin x 2 cos x C.
du dx; v sin x
18. Определенный интеграл
• Пусть на отрезке [ab] задана непрерывнаяфункция y=f(x)
19.
Внутри каждого отрезка выберем некоторую точку .x0 < 1 < x1, x1 < < x2, … , xn-1 < n < xn.
Найдем значения функции в этих точках и составим
выражение, которое называется интегральной суммой
для функции f(x) на отрезке [a, b].
2
n
Sn = f( 1) x1 + f( 2) x2 + … + f( n) xn = f ( i ) xi
i 1
Определение: Если при любых разбиениях отрезка
[a, b] таких, что max xi 0 иn произвольном выборе
точек i интегральная сумма S n f ( i ) xi
i 1
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]:
20.
Свойства определенного интеграла.b
b
a
a
1. Af ( x ) dx A f ( x ) dx;
a
2. f ( x)dx 0
a
b
b
b
a
a
a
3. ( f1 ( x) f 2 ( x)) dx f1 ( x)dx f 2 ( x)dx
4. Если f(x) (x) на отрезке [a, b] a < b, то
b
b
a
a
f ( x)dx ( x)dx
21.
5.Если m и M – соответственно наименьшее и наибольшеезначения функции f(x) на отрезке [a, b], то:
b
m(b a) f ( x)dx M (b a)
a
6. Если функция f(x) непрерывна на отрезке [a, b], то на
этом отрезке существует точка такая, что
b
a
a
b
7. f ( x)dx f ( x)dx
22.
8. Для произвольных чисел a, b, c справедливо равенство:Теорема: (Теорема Ньютона – Лейбница)
Если
функция F(x) – какая- либо первообразная от непрерывной
функции f(x), то
b
f ( x)dx F (b) F (a) = F(x)
a
b
a
23. Некоторые приложения определённого интеграла. 1.Вычисление площадей плоских фигур
Пример.1
0
/2
/ 2
/2
x
sin
t
;
1
2
2
1 x 2 dx
1
sin
t
cos
tdt
cos
tdt (1 cos 2t )dt
2 0
0; / 2 0
0
1 1
/2 1
t sin 2t sin .
2 2
4
0 4 4
Некоторые приложения
определённого интеграла.
1.Вычисление площадей плоских
фигур
24.
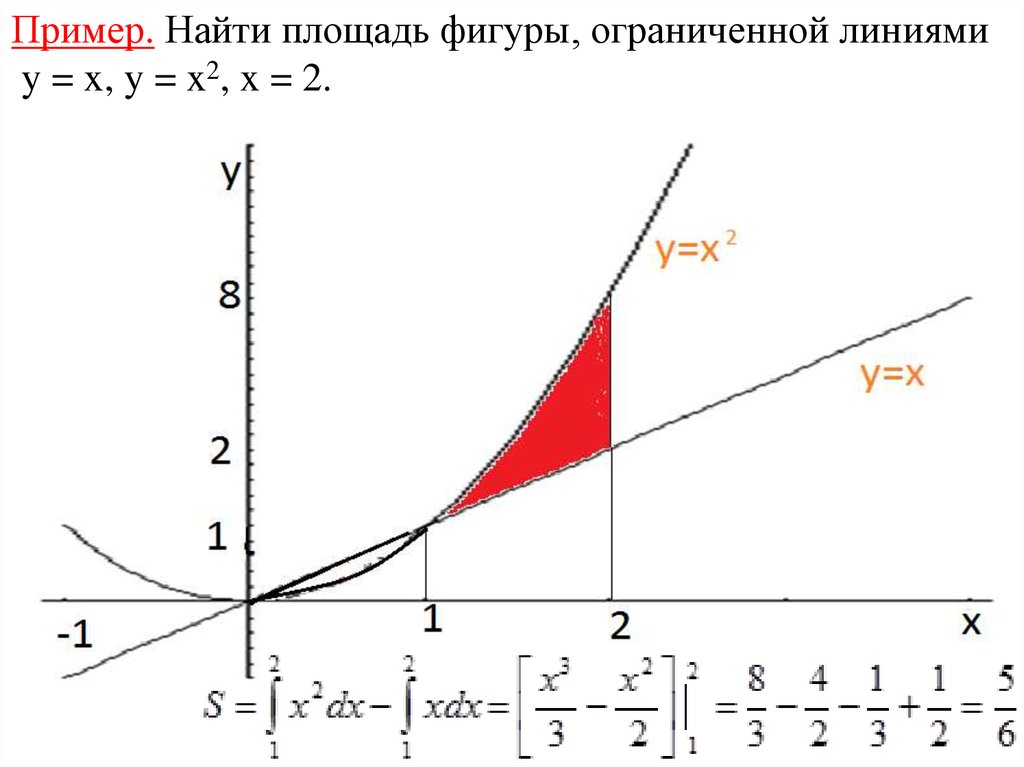
Пример. Найти площадь фигуры, ограниченной линиямиy = x, y = x2, x = 2.
25. 2. Вычисление работы переменной силы.
• Пример. Найти работу для растяженияпружины от равновесного состояния на
величину 0,1 м., если коэффициент
упругости k=100 Н/м
• Решение. Сила Гука F=kx. Работа
l
2
2
2
l
x
l
0,1
A kxdx k
k 100
0,5 Дж
2 0
2
2
0
26. 3.Вычисление среднего значения функции
• Средним значением функции на отрезке[a,b] называется величина
b
1
f
f ( x)dx
b-a a
• Пример. Найти среднее значение sinx на
отрезке от 0 до π.
1
1
2
f
sin xdx cos x 0
-0 0
















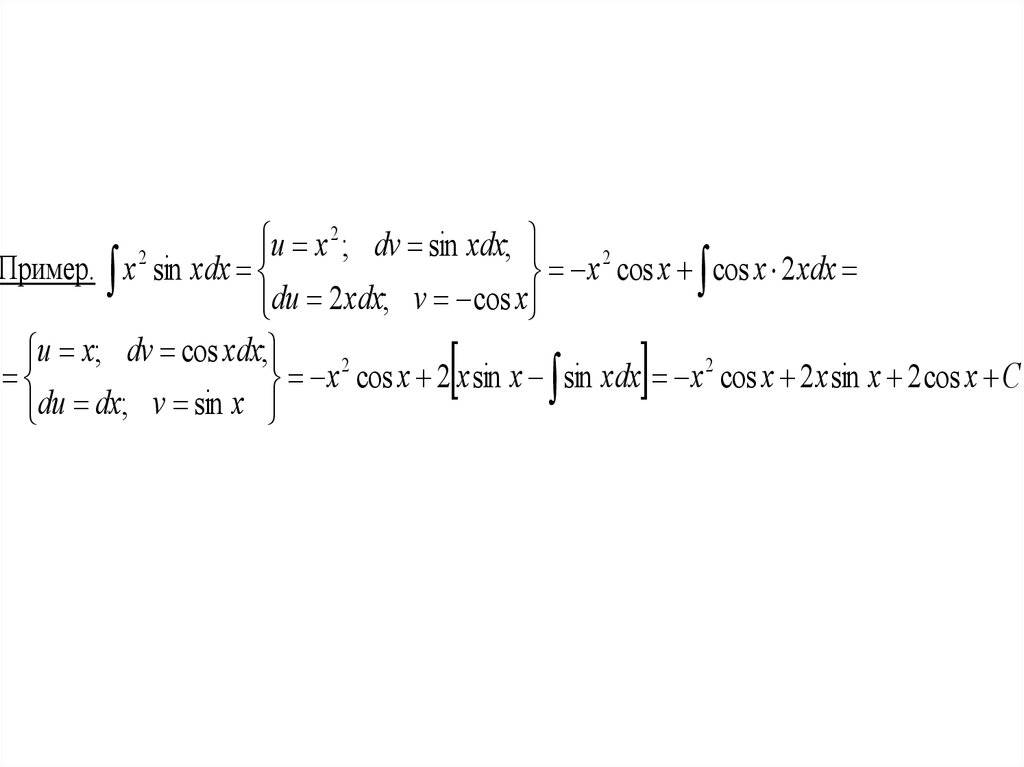








 Математика
Математика








