Похожие презентации:
Применение квадратичных форм к исследованию кривых и поверхностей второго порядка. Тема 17
1.
§17. Применениеквадратичных форм к
исследованию кривых и
поверхностей второго
порядка
2.
Пусть кривая второго порядка заданауравнением
2
2
a11 x 2 a12 xy a 22 y bx cy f 0.
Рассмотрим квадратичную форму
L ( x , y ) a11 x 2 2 a12 xy a 22 y 2 .
Канонический вид
L ( x ', y ') 1 x ' 2 y ' .
2
2
3.
Если1 2 0,
то кривая имеет эллиптический вид;
если
1 2 0,
то кривая имеет гиперболический вид;
если
1 2 0,
то кривая имеет параболический вид.
4.
Пример. Определить вид кривой2 x 2 xy 2 y 1 0.
Решение. Составим матрицу
2 1
.
1 2
2
Так как
1 2
2
2 1
3 0,
1 2
то кривая имеет эллиптический вид.
5.
Пример. Привести к каноническому видууравнение кривой
2
2
5 x 4 xy 8 y 8 x 14 y 5 0
Сделать рисунок.
Решение. Обозначим
L ( x , y ) 5 x 2 4 xy 8 y 2 .
Матрица этой квадратичной формы имеет вид
5 2
.
2 8
Составим характеристическое уравнение
5
2
2
8
13 36 0.
2
6.
Собственные числа:1 4, 2 9.
Найдем собственные векторы.
1 4.
x1 2 x2 0,
x1 2 x2 .
2 x1 4 x2 0,
Пусть
x2 t ,
тогда
x1 2t.
7.
Поэтому2t 2
x
t, t R, t 0
t 1
— собственные векторы, соответствующие
собственному числу 1 4.
1
Нормируем эти векторы:
| x1 | ( 2) 2 12 5;
2
5
.
x1 '
1
5
8.
2 9.4 x1 2 x2 0,
x2 2 x1.
2 x1 x2 0,
Пусть
x1 t ,
тогда
Поэтому
x 2 2t .
t 1
x t, t R, t 0
2t 2
— собственные векторы, соответствующие
собственному числу 2 9.
2
9.
Нормируем эти векторы:| x 2 | 12 2 2 5;
1
5
.
x2 '
2
5
10.
Матрица преобразования координат (матрицаповорота):
2
5
T
1
5
1
5
.
2
5
Формулы преобразования осей координат
2
1
x
x
'
y
',
5
5
y 1 x ' 2 y '.
5
5
11.
Подставив в уравнение данной кривойвыражения для x и y
2
2
1
1
2 1
2
2
2
1
5
x '
y ' 4
x '
y '
x '
y ' 8
x '
y '
5
5 5
5 5
5
5
5
1
2
2
1
8
x '
y ' 14
x '
y ' 5 0.
5
5
5
5
Так как с помощью указанного преобразования
координат квадратичная форма приводится к
каноническому виду, то получим
2
36
4x ' 9 y '
x '
y ' 5 0.
5
5
2
2
12.
Выделим полные квадраты2
1
1 1
1 1
2
2
4x '
x ' 4 x '
x ' 4 x ' 2x '
2 2 5 80 80
5
2 5
2
1
1
1
1
4 x '
4 x '
;
80
20
4
5
4
5
2
2
36
1 4 4 4
2 4
2
9y'
y ' 9 y '
y ' 9 y ' 2 y '
2 5 5 5
5
5
2
2
2
2 4
2 36
9 y '
9 y '
.
5
5
5
5
13.
Подставим2
2
1
2
1 36
4 x '
9 y '
20 5 5 0;
4 5
5
2
2
1
2 9
4 x '
9 y '
4.
4 5
5
Выполним параллельный перенос по
формулам
1
x ' x " 4 5 ,
y ' y " 2 .
5
14.
Окончательно получим9
4x" 9 y " ;
4
x "2 y "2
1
9
1
16
4
2
2
— эллипс с полуосями
3
1
a , b .
4
2
15.
yy'
x'
y"
1
1
x
4 5
1
y
x
x"
2
5
16.
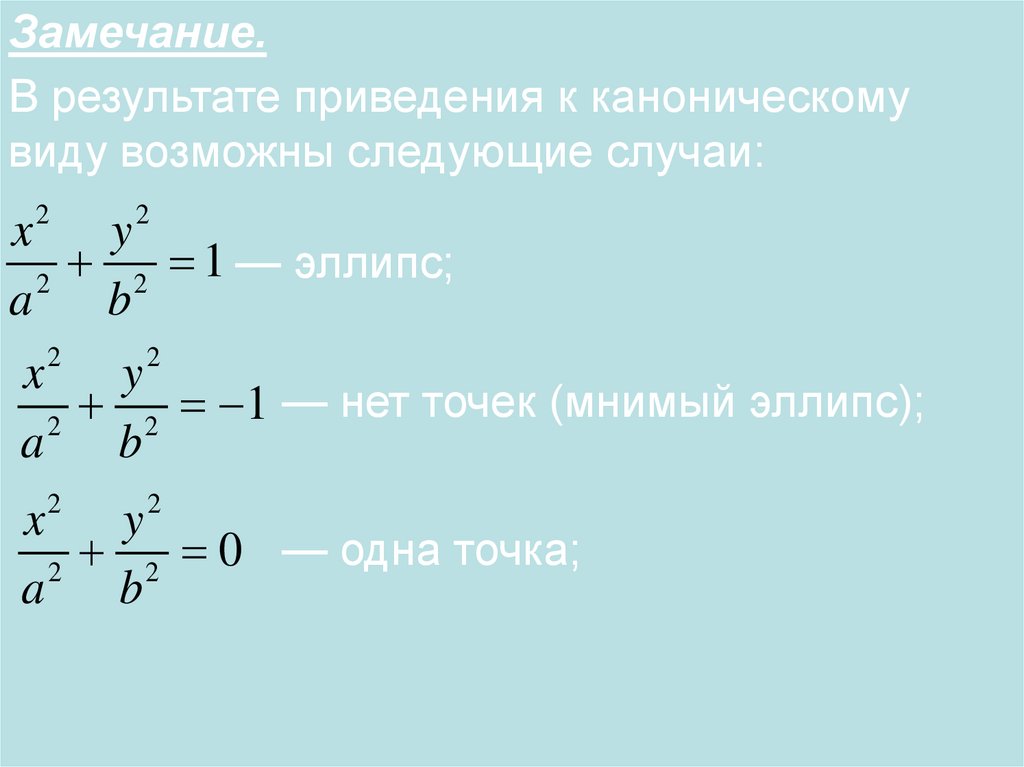
Замечание.В результате приведения к каноническому
виду возможны следующие случаи:
2
2
2
2
x
y
2 1 — эллипс;
2
a
b
x
y
2 1 — нет точек (мнимый эллипс);
2
a
b
x2 y2
2 0 — одна точка;
2
a
b
17.
x2 y22 1 — гипербола с действительной
2
a
b
осью Ox;
x2 y2
2 1 — гипербола с действительной
2
a
b
осью Oy;
2
2
x
y
2 0 — пара пересекающихся прямых;
2
a
b
18.
y 2 px — парабола (любые варианты);2
y2 a2
— пара параллельных прямых;
y 2 a 2 — нет точек (пара мнимых
параллельных прямых);
y 0
2
— одна прямая.

















 Математика
Математика








