Похожие презентации:
Кривые второго порядка
1. Кривые второго порядка
1. Эллипс.2. Гипербола.
3. Парабола.
2. Определение
Кривыми второго порядканазываются линии, уравнения
которых являются уравнениями
второй степени с двумя
переменными.
3. Эллипс
Эллипсом называется линия, имеющая внекоторой системе координат уравнение
2
2
x
y
2
2 1,
a
b
где x и y – переменные;
a и b – положительные числа, a ≥ b.
4. Преобразуем каноническое уравнение эллипса к одному из следующих видов:
b 2 2y a x
a
x a; a
2a – большая ось,
a 2 2
x b y
b
y b; b
2b – малая ось
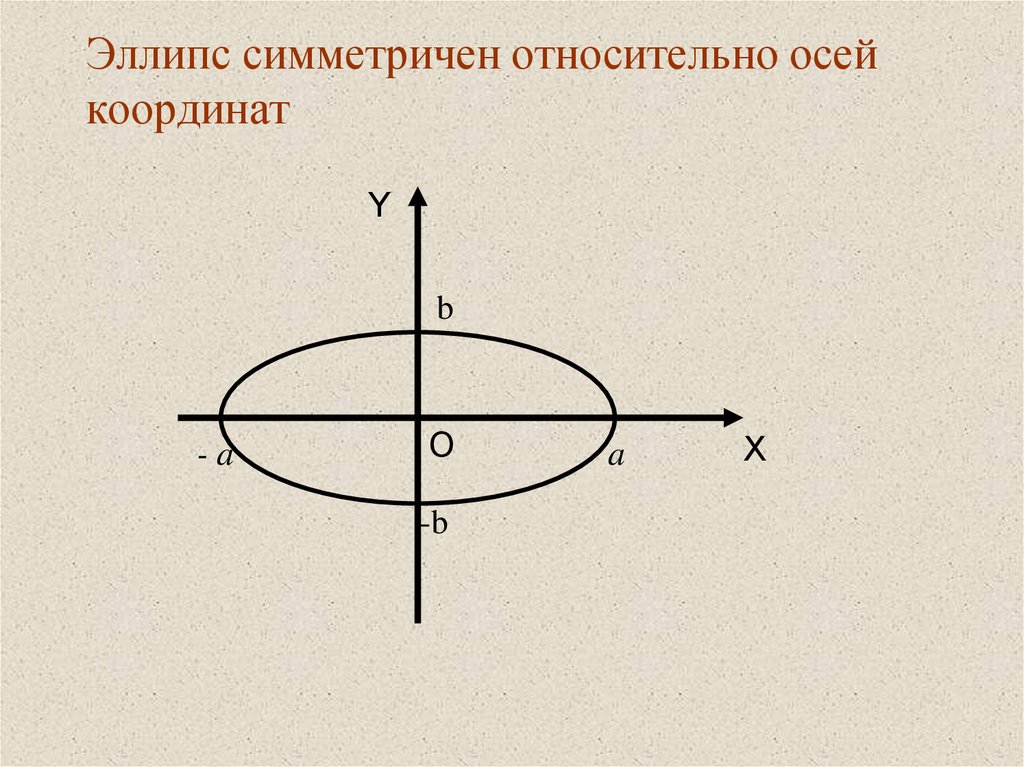
5. Эллипс симметричен относительно осей координат
Yb
-a
O
-b
a
X
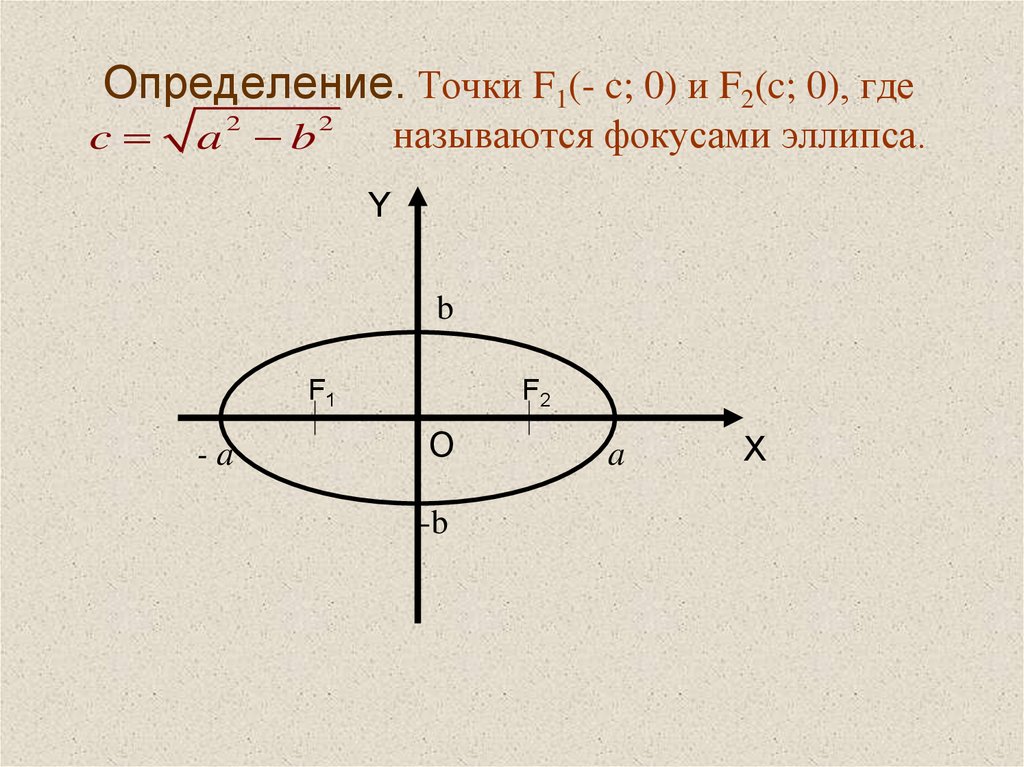
6. Определение. Точки F1(- c; 0) и F2(c; 0), где называются фокусами эллипса.
Определение. Точки F1(- c; 0) и F2(c; 0), гдеc
a b
2
называются фокусами эллипса.
2
Y
b
F1
-a
F2
O
-b
a
X
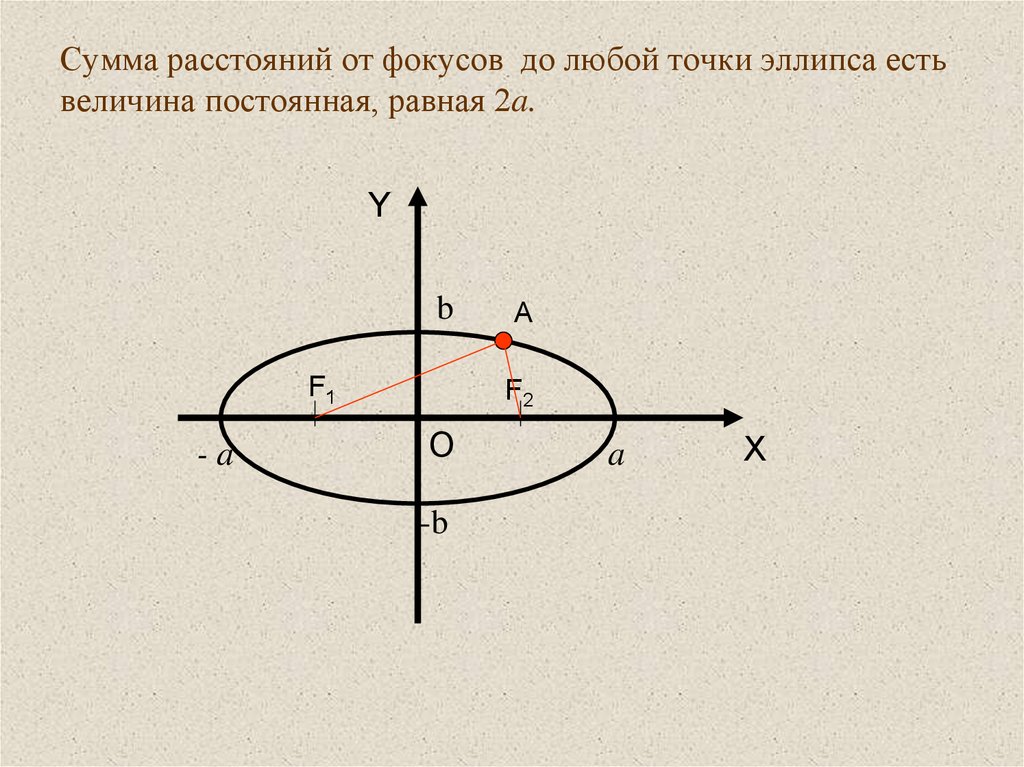
7. Сумма расстояний от фокусов до любой точки эллипса есть величина постоянная, равная 2a.
Yb
F1
-a
A
F2
O
-b
a
X
8. Определение. Отношение расстояния между фокусами к большой оси эллипса называется его эксцентриситетом.
c,
a
0 1
Частным случаем эллипса является окружность.
x y 1,
2
2
c a a 0,
2
x x y y
2
0
0
2
R
2
2
0
9. Пример. Покажите, что уравнение
x y 2 x 6 y 15 02
2
является уравнением окружности, и найдите её
радиус.
Решение.
x
2
2 x 1 1 y 6 y 9 9 15 0
2
x 1 y 3
2
2
x0 1,
y0 3,
25
R 5
10.
ГиперболаГиперболой называется линия, имеющая в
некоторой системе координат уравнение
2
2
x
y
2
2 1,
a
b
где x и y – переменные;
a и b – положительные числа.
11. Преобразуем каноническое уравнение гиперболы к одному из следующих видов:
b 2 2y
x a
a
a 2 2
x y b
b
y R
x ; a a;
2a – действительная ось,
2b – мнимая ось
b
b
y x u y x - асимптоты
a
a
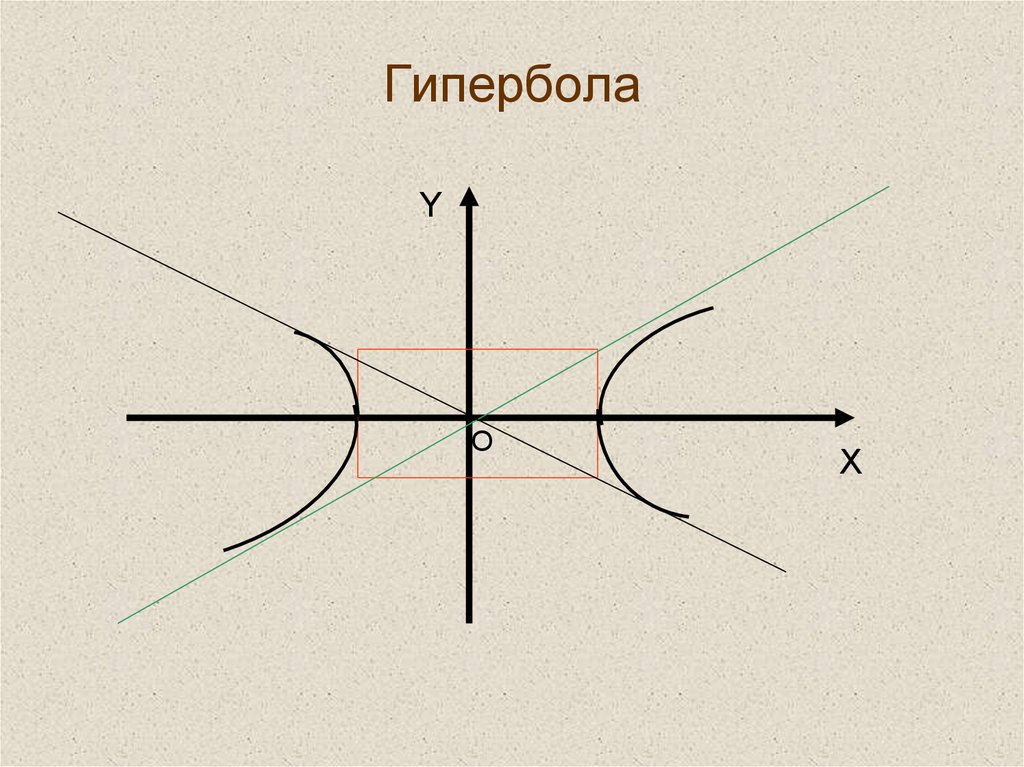
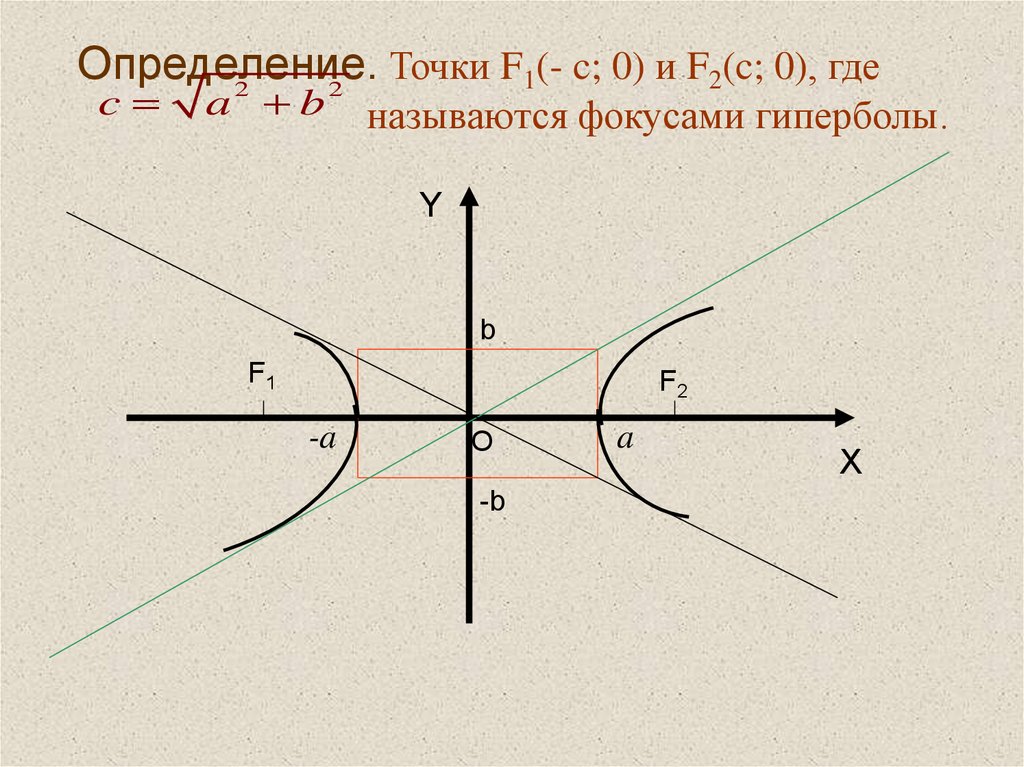
12. Гипербола
YO
X
13.
Определение.Точки F1(- c; 0) и F2(c; 0), где
2
2
c
a b
называются фокусами гиперболы.
Y
b
F1
F2
-a
O
-b
a
X
14. Определение. Отношение расстояния между фокусами и действительной оси гиперболы называется его эксцентриситетом.
c,
a
1
Определение. Равносторонней называется
гипербола у которой a = b.
k
y
x
15. Пример. Найти каноническое уравнение эллипса, фокусы которого совпадают с фокусами гиперболы
22
x
y
1
16
9
и эксцентриситет которого равен 0,5.
Решение.
c
cГ aГ bГ 16 9 5,
0,5 откуда a 2c 2 5 10
aЭ
c aЭ bЭ , 25 100 bЭ , bЭ 75.
2
2
2
2
2
2
x
y
1
100 75
Э
16. Парабола
Определение. Параболой называется линия,имеющая в некоторой системе координат
уравнение
y ax bx c
2
x и y – переменные;
a, b и c – действительные числа, a ≠ 0
17. Преобразуем уравнение y = ax2 + bx + c
bD
b
D
y a x 2 a x
2a 4a
2a 4a
2
2
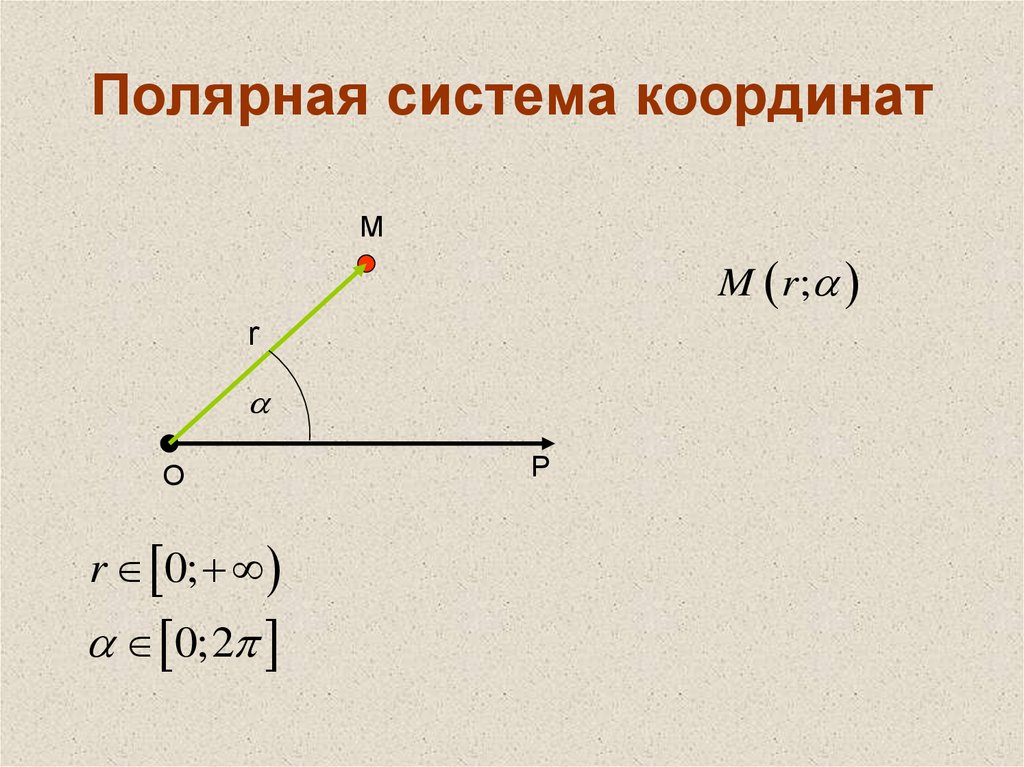
18. Полярная система координат
МM r ;
r
О
r 0;
0;2
Р
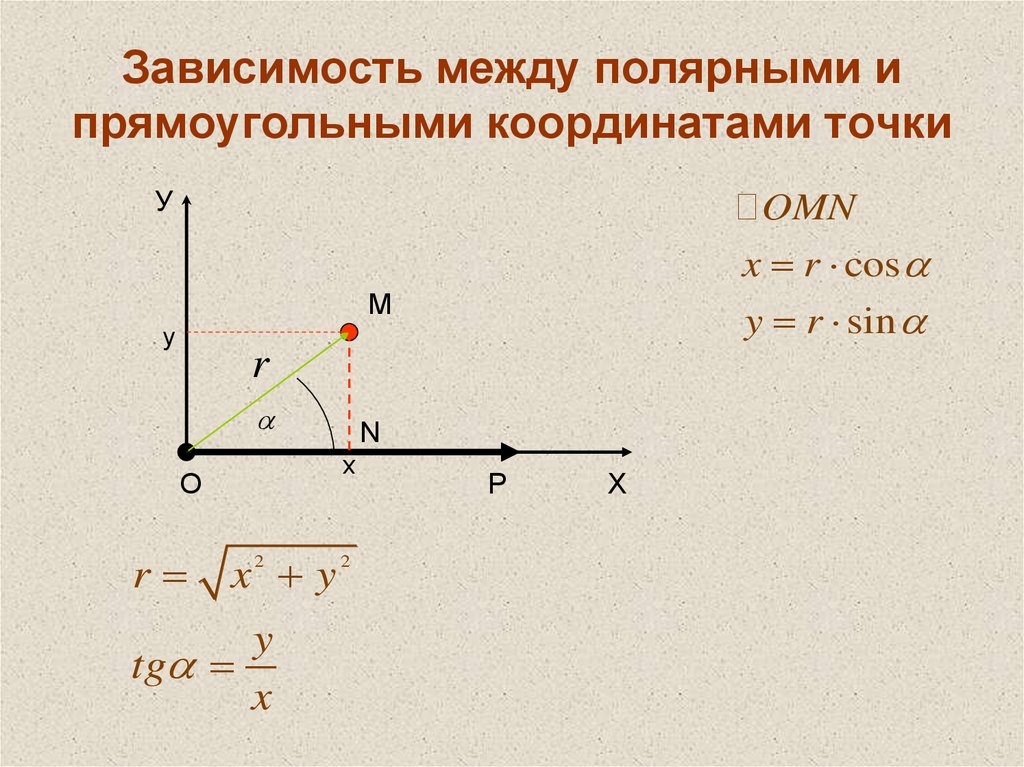
19. Зависимость между полярными и прямоугольными координатами точки
УOMN
x r cos
М
у
y r sin
r
х
О
r
N
x y
2
y
tg
x
2
Р
Х
20. Пример. Найти декартовы координаты точки М, полярные координаты которой
5;2 / 3 .Решение.
У
x r cos
у
y r sin
М
x 5 cos 2
5
2
х
О
3
Р
Х
5 5 3
M ;
2 2
5
3
3
y 5 sin 2
5 3
3
2
21. Пример. Найти полярные координаты точки М, декартовы координаты которой (5; - 5).
Решение.r
У
-5
Х
М
2
2
y
tg
x
5
О
x y
r 5 5 5 2
2
2
5
tg
1
5
7
2
4
4
7
M 5 2;
4
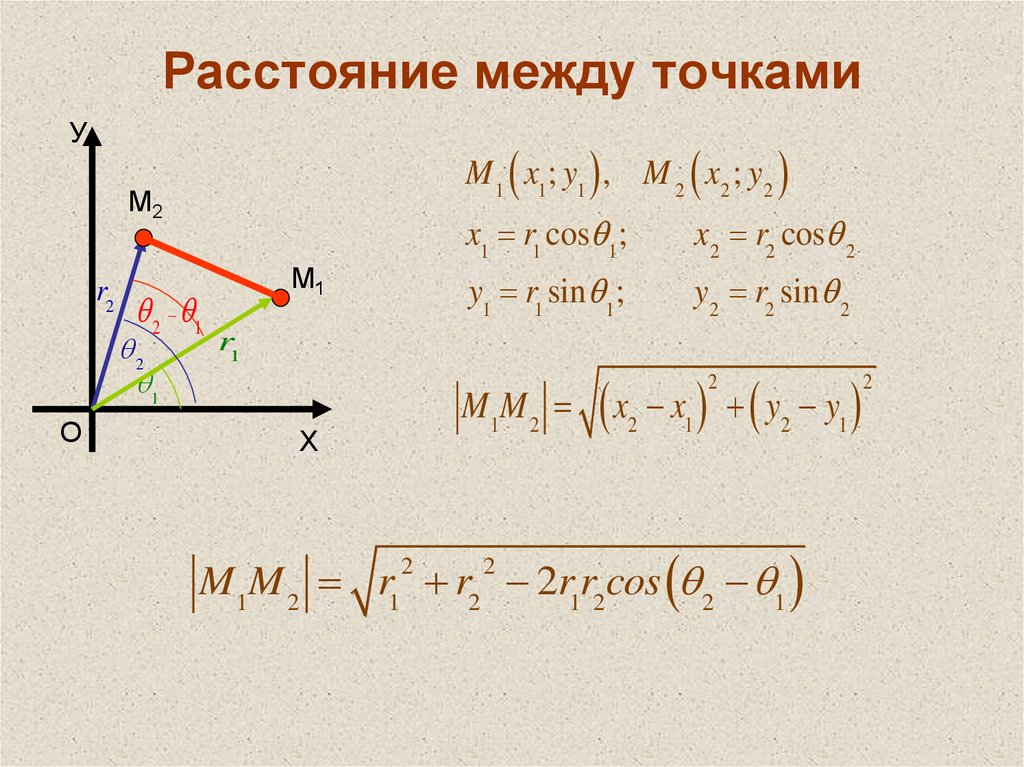
22. Расстояние между точками
УM 1 x1; y1 , M 2 x2 ; y2
М2
r2
2 1
2
1
О
М1
x1 r1 cos 1;
x2 r2 cos 2
y1 r1 sin 1;
y2 r2 sin 2
r1
M1M 2
Х
x
2
x1 y2 y1
2
M1M 2 r1 r2 2r1r2cos 2 1
2
2
2
23. Уравнение линии в полярной системе координат
Уравнение прямой линии:Ar cos Br sin C 0
- C
r=
A cos q + B sin q
Уравнение кривой второго порядка:
q
r=
; q О[0; 2p )
1- e cos q











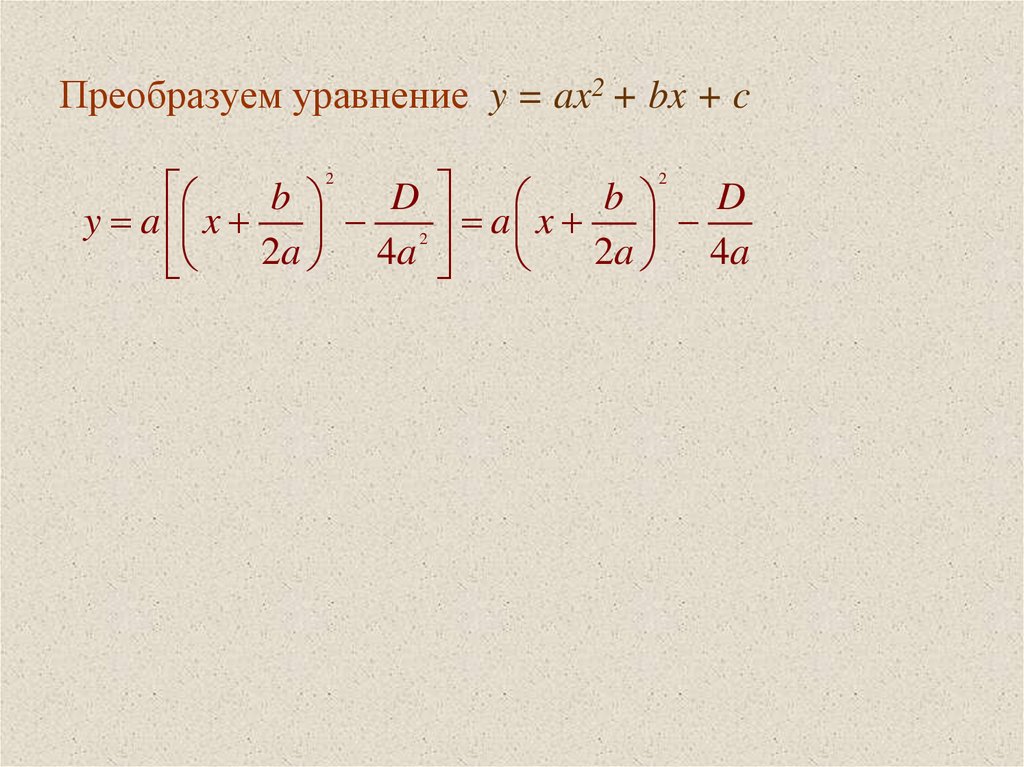



 Математика
Математика








