Похожие презентации:
Пифагоровы тройки
1.
Работу выполнилаученица 9 «а» класса
МАОУ СОШ №1
Коренева Кристина
2.
Цель данной работы –обосновать теоретическую и
практическую значимость
пифагоровых троек в области
математики и в жизнедеятельности
человека.
Задачи:
1)
Установить способы получения
пифагоровых чисел;
2)
Изучить свойства примитивных
пифагоровых троек, составить их
таблицу;
3)
Познакомиться с материалом,
связанным с теоремой Ферма и
попытками ученых всего мира
доказать ее.
4) Выявить практическое
применение пифагоровых троек.
Объект и исследования:
уравнение Пифагора.
Предмет исследования:
пифагоровы тройки.
Методы исследования:
анализ и синтез полученных фактов из
литературы по теме, систематизация
полученных знаний, моделирование
реальных ситуаций.
3.
Задача Пифагора: решить внатуральных числах уравнение
Тройка натуральных чисел (x;y;z),
которая является решением данного
уравнения называется пифагоровой
тройкой.
4.
5.
6.
А теперь внимание! В нижней строке естьквадратные числа! Первое из них 9 = 3^2, над ними
16 = 4^2 и 25 = 5^2 - знакомая нам пифагорова
тройка 3, 4, 5.
7.
Пусть (x, y, z,) – пифагорова тройка и x –нечетное число.Тогда,
По этому правилу можно
получить уже известные
нам тройки:
8.
9.
10.
Тройки чисел (х; у; z), не имеющих общих делителей, больше 1, называютсяпримитивными (или простейшими).
Например: (3,4,5), (5,12,13), (8,15,17), (9,40,41).
Ясно, что если (х,у, z) – примитивная тройка, то для любого натурального
числа n, тройка ( nx, ny, nz ) тоже будет примитивной.
Пифагор нашел формулы для нахождения примитивных троек, которые в
современной символике могут быть записаны так:
11.
xn + yn = zn.
12.
13.
Построить из спичек разносторонний треугольник с высотой 12.1 способ
(3,4,5)
(4,3,5)
2 способ
умн. на 4
умн. на 3
(12,16,20)
(12,9,15)
Так как 16+9=25, получаем
Треугольник со сторонами
12, 15, 25 спичек.
(3,4,5)
(12,5,17)
умн. на 3
(9,12,15)
Так как 9+5=14, получаем
треугольник со сторонами
12, 15,14 спичек.
14.
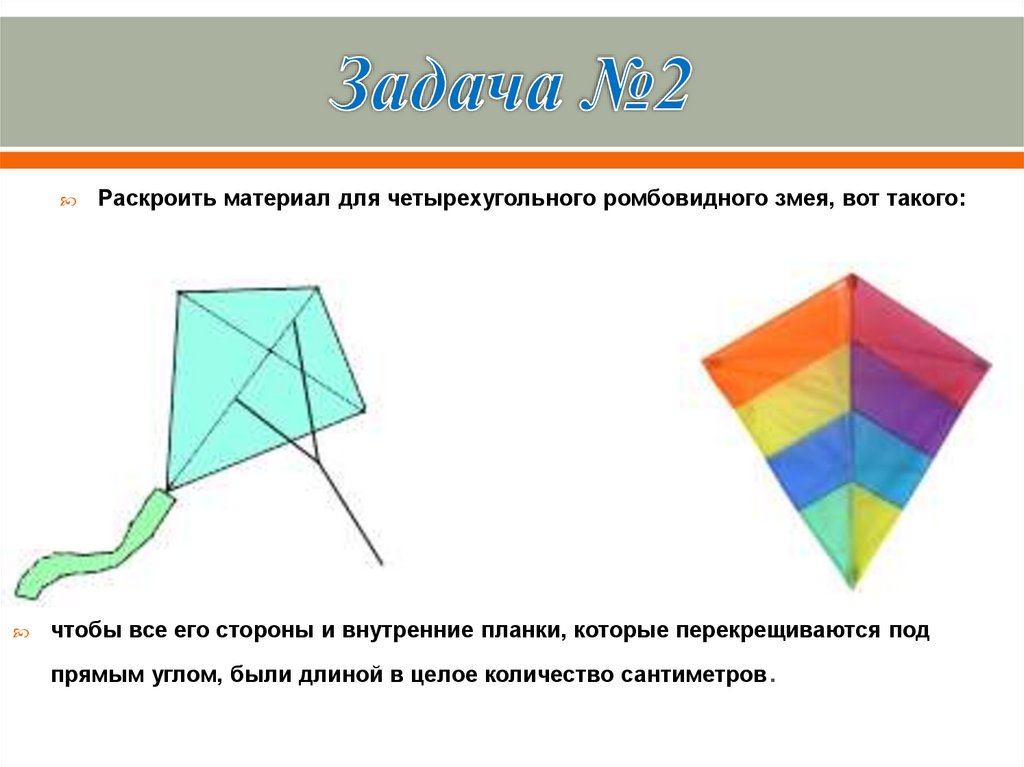
Раскроить материал для четырехугольного ромбовидного змея, вот такого:чтобы все его стороны и внутренние планки, которые перекрещиваются под
прямым углом, были длиной в целое количество сантиметров
.
15.
При оформлении фасада дома мозаикой, требуются разноцветные равныепрямоугольные треугольники из стекла, с целочисленными сторонами и с
катетом 10 см. Требуется определить, какими должны быть другие
стороны данных треугольников.
Решение:
Заданный катет – четное число,
значит х = 10 = 2mn, где m>n и они взаимно
простые числа. Возможна единственная
комбинация m и n – это 5 и 1. Так как 2*5*1=10.
Остальные стороны равняются у=m^2-n^2=24,
z=m^2+n^2=26. Таким образом, ответ – это
треугольники со сторонами 10см, 24 см и 26 см.
16.
17.
Известно, что угол наклона пандуса для передвижения инвалидов наколясках внутри и снаружи здания должен быть не больше 5 градусов и
высотой, не превышающей 80 см. От жильцов дома, строительной
организации поступил заказ - построить пандус для инвалидаколясочника. Какой длины должен быть подъем пандуса, расстояние от
начало подъема до подъезда и высота, удовлетворяющие этим
требованиям?
18.
Решение: Можно считать,что пандус имеет форму
прямоугольного треугольника.
Тангенс 5 градусов приближенно
равен 0,0875. Использую таблицу
примитивных пифагоровых
троек, можно легко найти нужную
тройку чисел, которая удовлетворяет
условию, что, катет, противолежащий
углу в 5 градусов в прямоугольном
треугольнике, должен быть не более
80 см. Учитывая реальность ситуации
подбором получаем, что нужные нам
тройки – (25,312,313) или (27,364,365).
Следовательно,пандус может иметь
длины 25 см, 312 см, 313 см
или
27 см, 364 см, 365 см.
19.
В заключении хочется отметить, что работа над проектом позволилаузнать материал, которого нет в школьной программе. К сожалению,
полностью показать все аспекты научной теории, связанной с уравнением
Пифагора и пифагоровыми тройками, а так же практические задачи из
алгебры, геометрии и практической деятельности человека,
рассмотренные в данной работе, не позволяет время. Однако, опираясь на
поставленные задачи, мне удалось раскрыть важность исследуемой темы.
Изначально были выявлены базовые теоретические знания, включающие
описание общих понятий об уравнении Пифагора и пифагоровых тройках.
На базе полученных знаний были выявлены способы их получения и
свойства. Теоретическая и практическая значимость исследования
состоит в том, что в нем на основе системного подхода представлена
роль, которую играет открытие пифагоровых троек в науке и в
жизнедеятельности человека.

















 Математика
Математика








