Похожие презентации:
Математическое моделирование РЭС в частотной области
1.
2.
Математическое моделированиеРЭС в частотной области
X ВЫХ ( j ) K ( j ) X ВХ ( j )
где X ВХ ( j ) и X ВЫХ ( j )
- спектры входного и выходного сигналов
Возможно использование матриц:
- классической теории Z, Y, A, H;
- волновой теории S, T.
3.
Формирование системы уравненийматематической модели РЭС с использованием
матриц классической теории
4.
5.
Формирование системы уравненийматематической модели РЭС
с использованием матрицы A
• для последовательного соединения четырехполюсников
A
a '11 a '' 21 a ''11 a ' 21
a ' 21 a '' 21
( a '11 a ''11 ) ( a ' 21 a '' 22 )
a '12 a ''12
a ' 21 a '' 21
a ' 21 a '' 21
a ' 21 a '' 21
a ' 21 a '' 22 a '' 21 a ' 22
a ' 21 a '' 21
6.
• для параллельного соединения четырехполюсниковA
a '11 a ''12 a ''11 a '12
a '12 a ''12
a '12 a ''12
a '12 a ''12
( a '11 a ''11 ) ( a ' 22 a '' 22 )
a ' 21 a '' 21
a '12 a ''12
a '12 a '' 22 a ''12 a ' 22
a '12 a ''12
• для последовательного соединения по входу и параллельного
соединения по выходу
A
( a '12 a ''12 ) ( a ' 21 a '' 21 )
a '11 a ''11
a ' 22 a '' 22
a '12 a '' 22 a ''12 a ' 21
a ' 22 a '' 22
a ' 21 a '' 22 a '' 21 a ' 21
a ' 22 a '' 22
a ' 22 a '' 22
a ' 22 a '' 22
7.
Формирование системы уравненийматематической модели РЭС
с использованием матрицы Y
8.
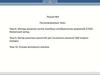
Y3Y2
Y1
Y5
Y4
9.
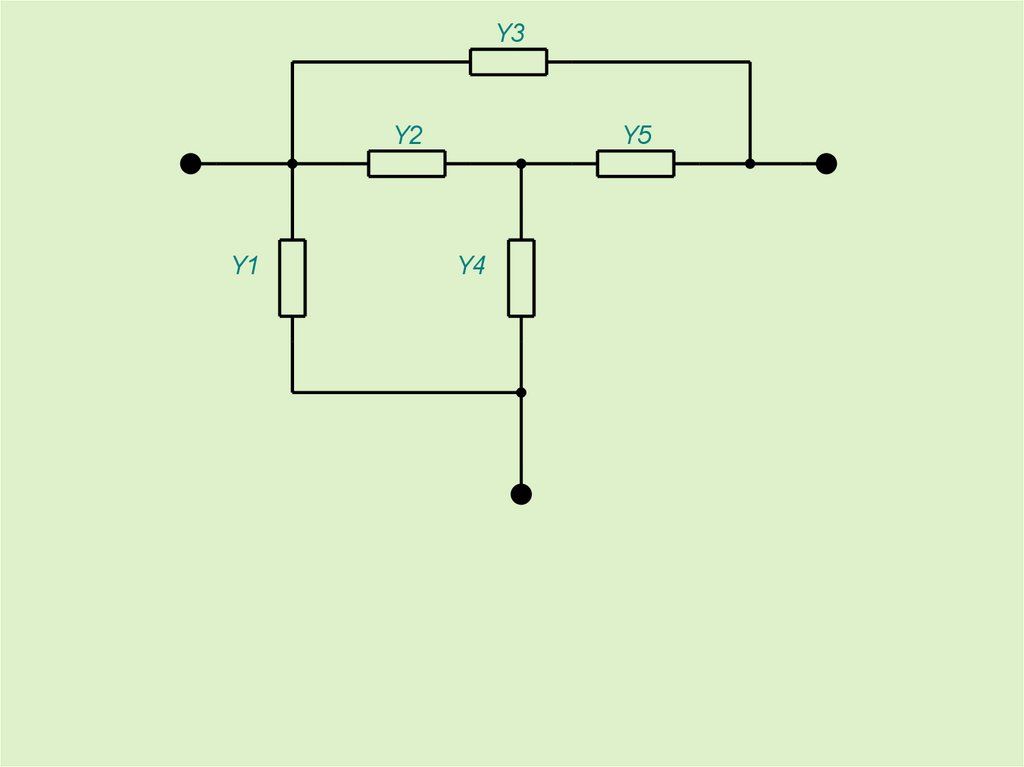
Y3Y2
Y1
Y5
Y4
10.
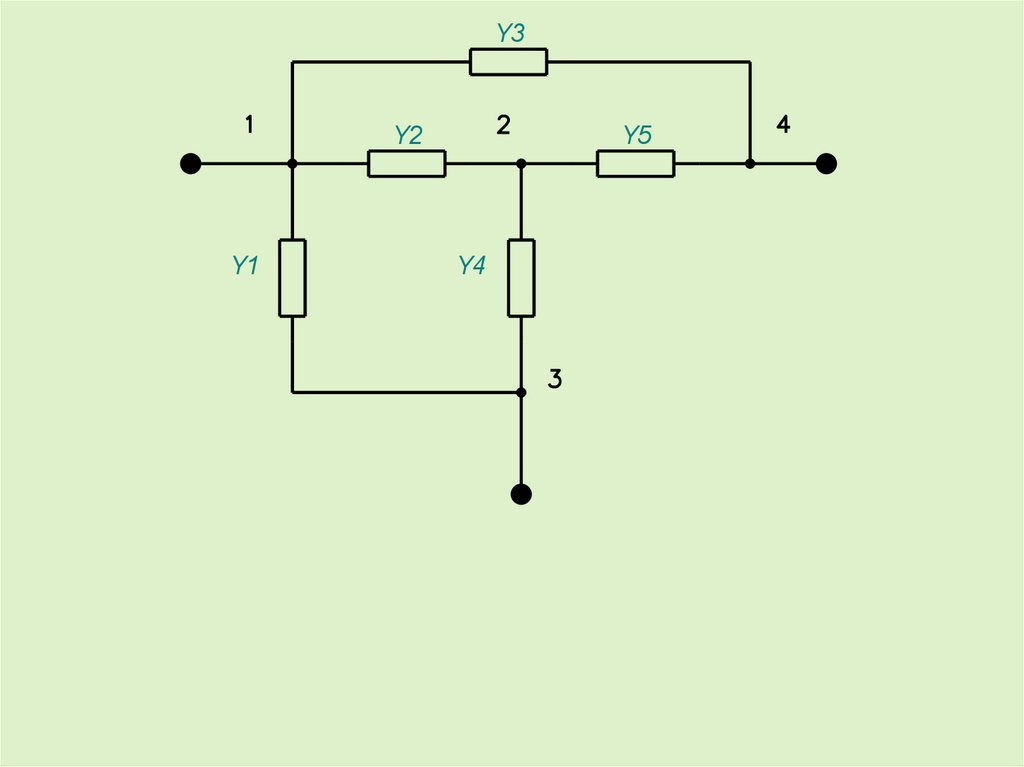
Y3Y2
Y1
Y=
Y5
Y4
11.
Y3Y2
Y1
Y1+Y2+Y3
Y=
Y5
Y4
12.
Y3Y2
Y1
Y5
Y4
Y1+Y2+Y3
Y=
Y2+Y4+Y5
Y1+Y4
Y3+Y5
13.
Y3Y2
Y1
Y1+Y2+Y3
Y=
Y5
Y4
-Y2
Y2+Y4+Y5
Y1+Y4
Y3+Y5
14.
Y3Y2
Y1
Y1+Y2+Y3
Y=
Y5
Y4
-Y2
Y2+Y4+Y5
-Y1
-Y4
Y1+Y4
-Y3
-Y5
0
Y3+Y5
15.
Y3Y2
Y1
Y=
Y1+Y2+Y3
-Y2
-Y1
-Y3
Y5
Y4
-Y2
Y2+Y4+Y5
-Y4
-Y5
-Y1
-Y4
Y1+Y4
0
-Y3
-Y5
0
Y3+Y5
16.
Y3Y2
Y1
Y5
Y4
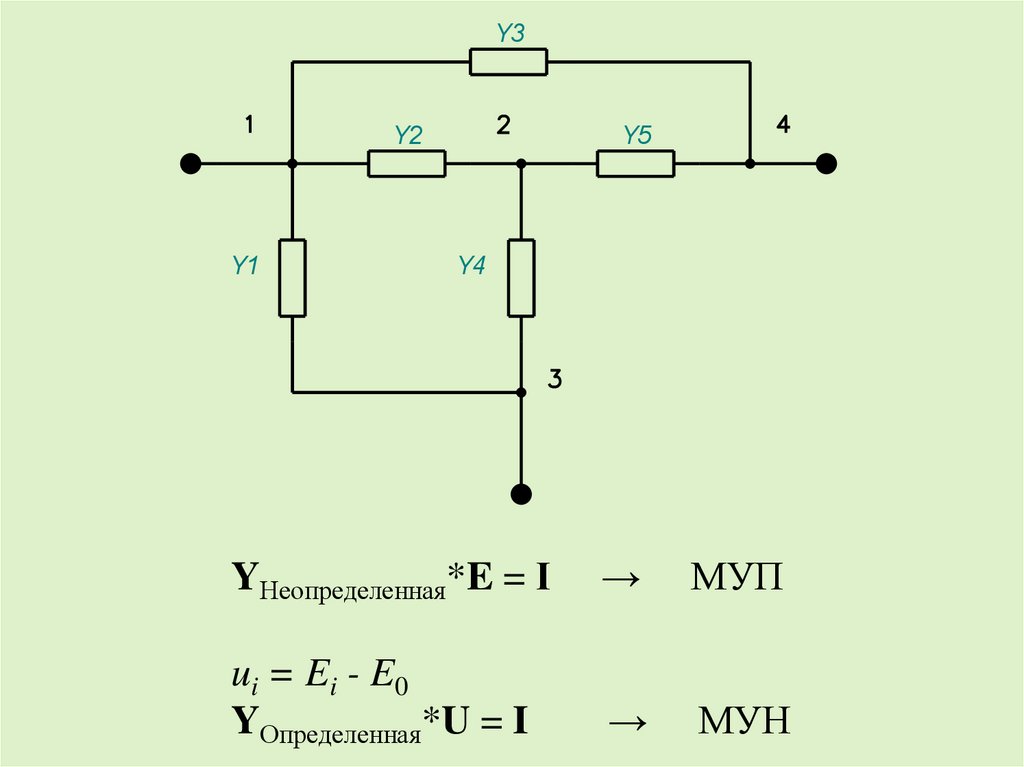
YНеопределенная*E = I
→
МУП
17.
Y3Y2
Y1
Y5
Y4
YНеопределенная*E = I
→
МУП
ui = Ei - E0
YОпределенная*U = I
→
МУН
18.
Y3Y2
Y1
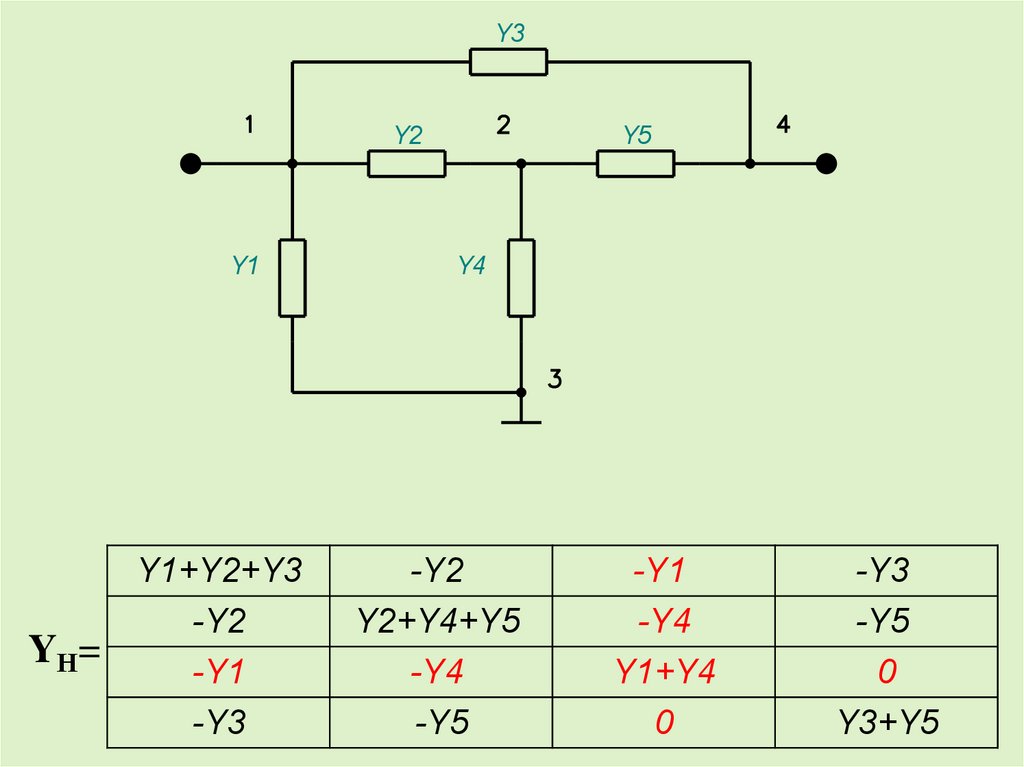
YН=
Y1+Y2+Y3
-Y2
-Y1
-Y3
Y5
Y4
-Y2
Y2+Y4+Y5
-Y4
-Y5
-Y1
-Y4
Y1+Y4
0
-Y3
-Y5
0
Y3+Y5
19.
Y3Y2
Y1
YН=
Y1+Y2+Y3
-Y2
-Y1
-Y3
Y5
Y4
-Y2
Y2+Y4+Y5
-Y4
-Y5
-Y1
-Y4
Y1+Y4
0
-Y3
-Y5
0
Y3+Y5
20.
Y3Y2
YО=
Y5
Y1
Y4
Y1+Y2+Y3
-Y2
-Y3
-Y2
Y2+Y4+Y5
-Y5
-Y3
-Y5
Y3+Y5
21.
Y3Y2
YО,0=
Y5
Y1
Y4
0
0
0
0
0
0
0
0
0
22.
Y3Y2
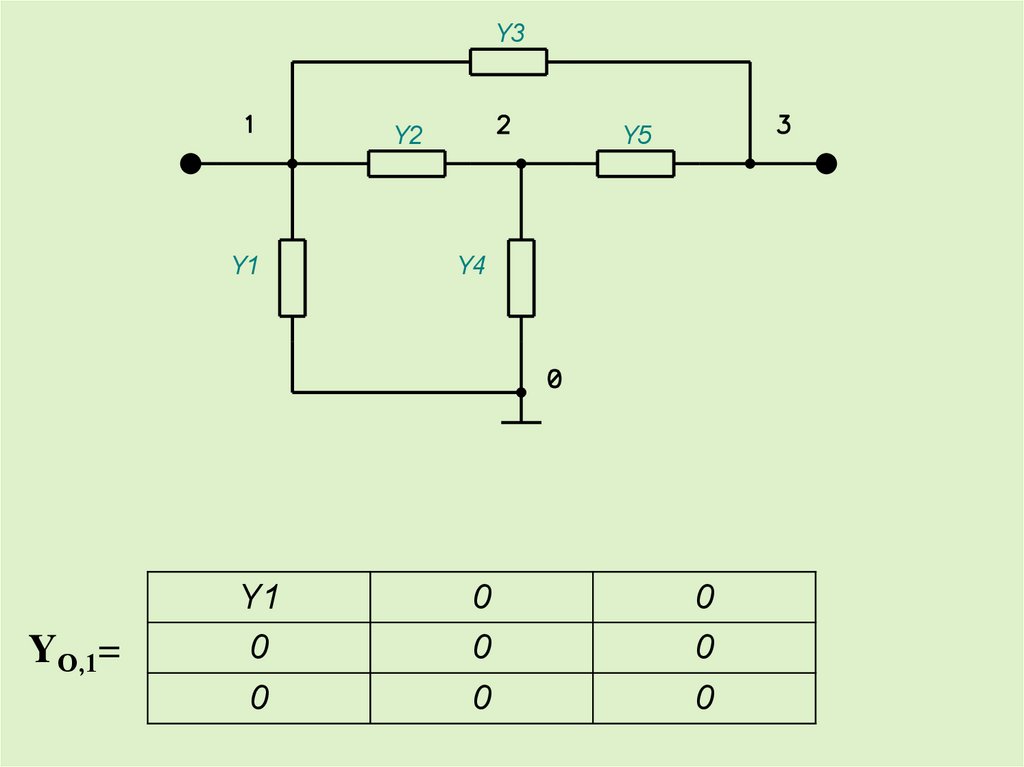
YО,1=
Y5
Y1
Y4
Y1
0
0
0
0
0
0
0
0
23.
Y3Y2
YО,2=
Y5
Y1
Y4
Y1+Y2
-Y2
0
-Y2
Y2
0
0
0
0
24.
Y3Y2
YО,5=
Y5
Y1
Y4
Y1+Y2+Y3
-Y2
-Y3
-Y2
Y2+Y4+Y5
-Y5
-Y3
-Y5
Y3+Y5
25.
Особенности моделирования нелинейных РЭСв частотной области
26.
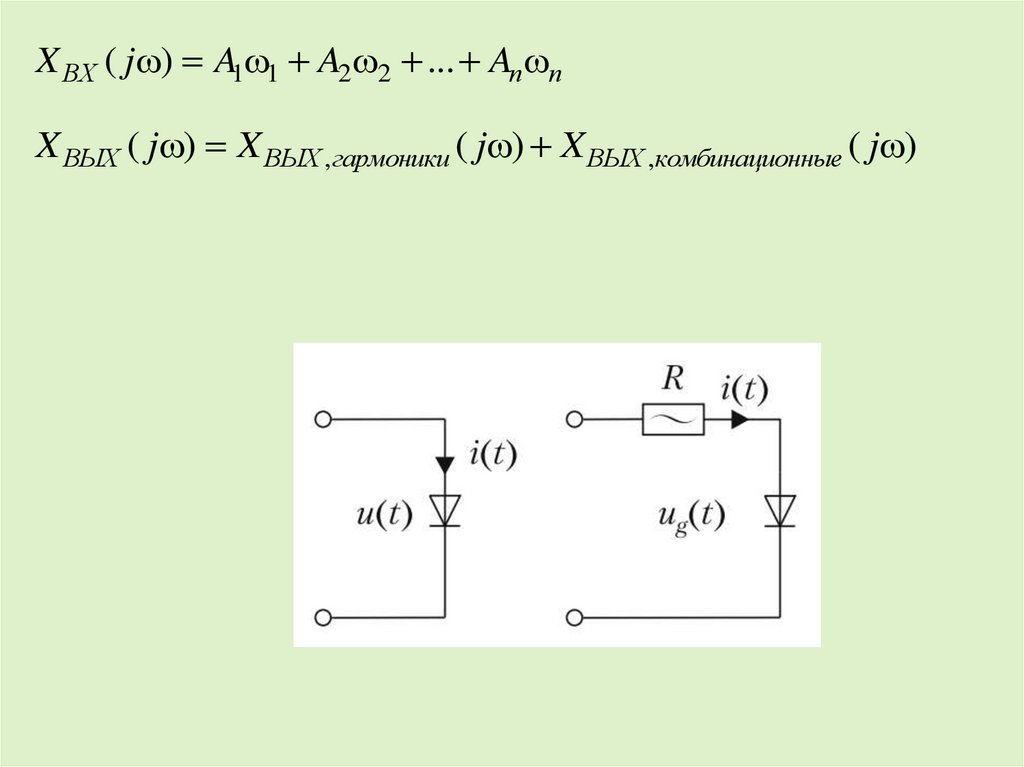
X ВХ ( j ) A1 1 A2 2 ... An nX ВЫХ ( j ) X ВЫХ ,гармоники ( j ) X ВЫХ ,комбинационные ( j )



















 Математика
Математика