Прогрессии. Результаты контрольной работы по алгебре №5

1.

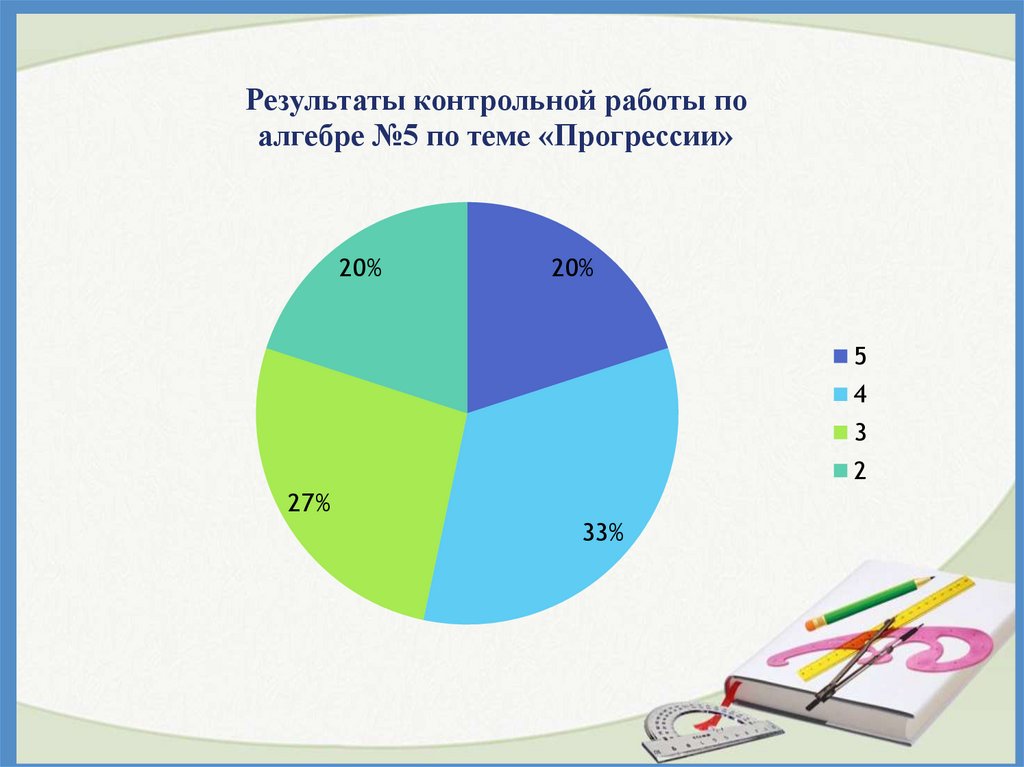
Результаты контрольной работы по
алгебре №5 по теме «Прогрессии»
20%
20%
5
4
3
2
27%
33%

2.

Глава 5. Элементы
комбинаторики, теории
вероятностей и статистики
Провела: учитель математики
высшей квалификационной категории
Петрова Наталья Анатольевна

3.

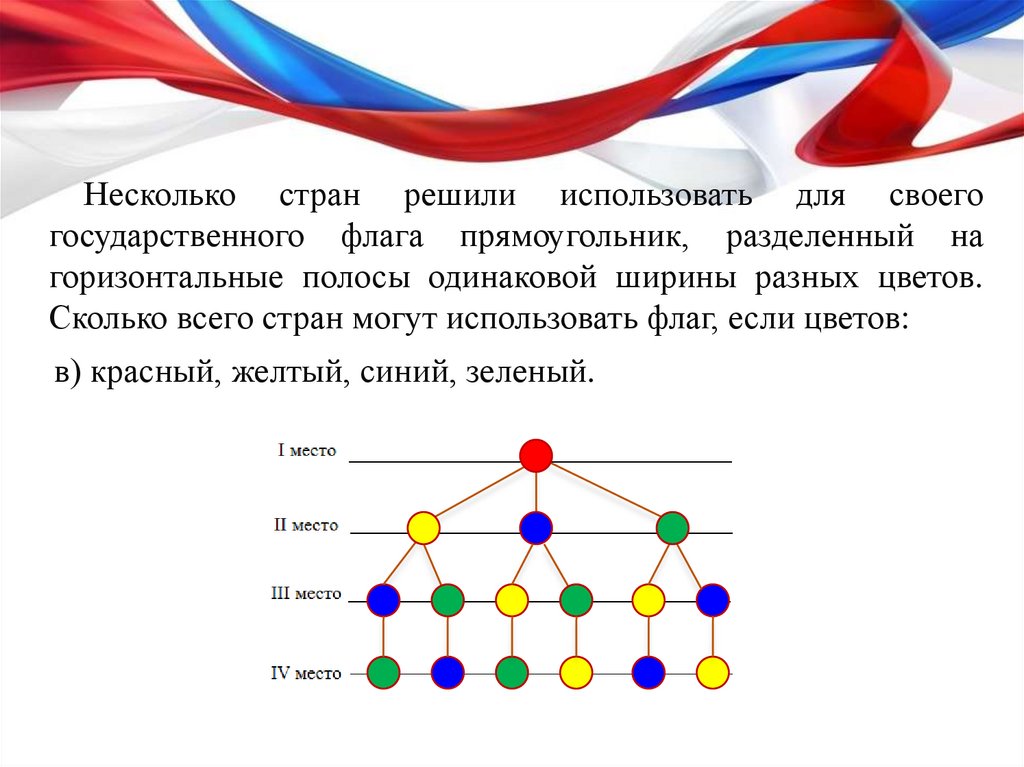
Несколько стран решили использовать для своего
государственного флага прямоугольник, разделенный на
горизонтальные полосы одинаковой ширины разных цветов.
Сколько всего стран могут использовать флаг, если цветов:
а) два вида. Желтый и голубой;
Ответ: 2 страны

4.

Несколько стран решили использовать для своего
государственного флага прямоугольник, разделенный на
горизонтальные полосы одинаковой ширины разных цветов.
Сколько всего стран могут использовать флаг, если цветов:
б) белый, синий и красный;
Ответ: 6 стран

5.

Несколько стран решили использовать для своего
государственного флага прямоугольник, разделенный на
горизонтальные полосы одинаковой ширины разных цветов.
Сколько всего стран могут использовать флаг, если цветов:
в) красный, желтый, синий, зеленый.

6.

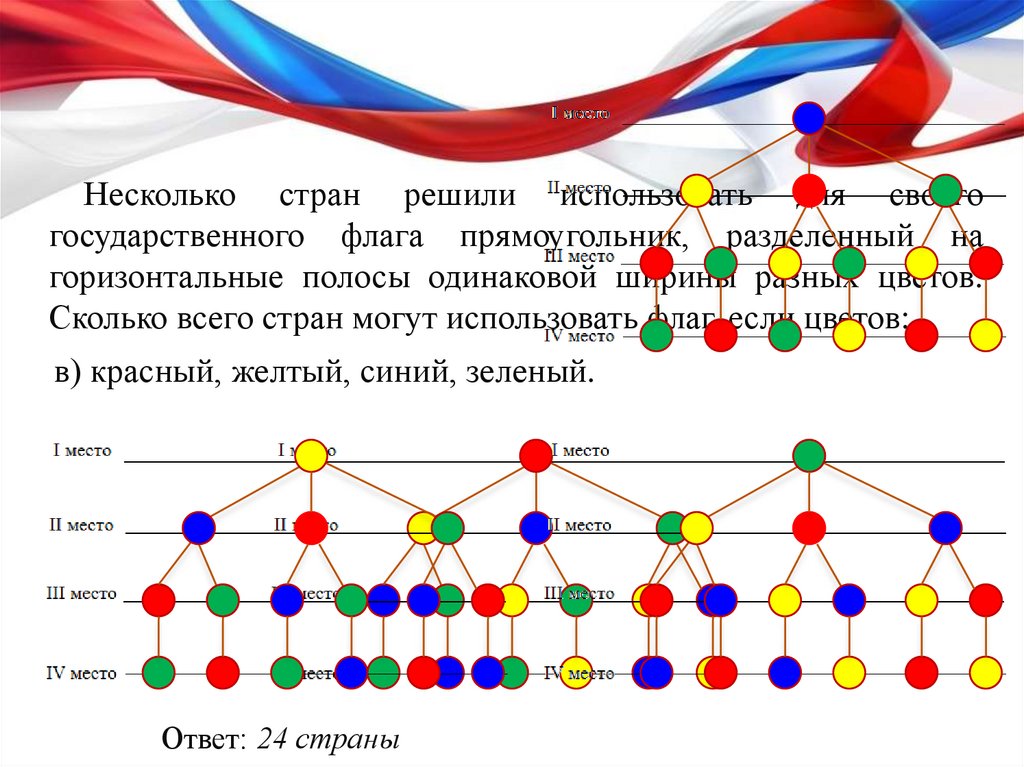
Несколько стран решили использовать для своего
государственного флага прямоугольник, разделенный на
горизонтальные полосы одинаковой ширины разных цветов.
Сколько всего стран могут использовать флаг, если цветов:
в) красный, желтый, синий, зеленый.
Ответ: 24 страны

7.

Задача 2
В школьной олимпиаде по математике приняли участие 30
девятиклассников. Для кодирования их работ учителю
необходимо было использовать только четные двузначные
числа, причем цифры не должны были повторяться и число
не должно заканчиваться нулем. Возможно ли кодирование
работ выбранным способом?
Таблица
9 ∙ 4 – 4 = 32
Ответ: кодирование возможно

8.

Глава 5, §18
*
.
Метод организованного перебора
Закрепить на первом месте комбинации один из
символов, принадлежащих множеству заданных в
задаче символов.
Продолжить перебор, последовательно закрепляя на
первом месте остальные символы.
Для выделенного случая выписать возможные
варианты, используя таблицу, схему или др.

9.

Глава 5, §18
*
Сформулируйте способ подсчета
числа
комбинаций,
который
позволяет сократить перебор всех
их возможных вариантов:
«Сколько трехзначных кодов можно составить из
цифр
1, 2, 3, 4, 5, если цифры кода не
повторяются?»

10.

Глава 5. Элементы комбинаторики, теории
вероятностей и статистики
Задачи организованного
перебора вариантов

11.

Глава 5, §18
*
.
Метод организованного перебора
(подсчет числа комбинаций из различных символов)
1. Закрепить на первом месте комбинации один из
символов, принадлежащих множеству заданных в
задаче символов.
2. Для выделенного случая выписать возможные
варианты, используя таблицу, схему или др. Подсчитать
полученное число вариантов.
3. Если по условию задачи каждый из символов может
занимать любую позицию, то общее количество
возможных вариантов равно произведению числа
вариантов, полученного для одного «закрепленного»
символа на количество заданных символов.

12.

Задача 3
Сколько
существует
способов
кодирования, если необходимо составить
трехзначный код, составленный из цифр 1,
2, 3 или 4, если цифры не должны
повторятся?

13.

Глава 5, §18
*
№ 18.4 (а)

14.

Глава 5, §18
*
.
Метод организованного перебора
(подсчет числа комбинаций из различных символов)
1. Закрепить на первом месте комбинации один из
символов, принадлежащих множеству заданных в
задаче символов.
2. Для выделенного случая выписать возможные
варианты, используя таблицу, схему или др. Подсчитать
полученное число вариантов.
3. Если по условию задачи каждый из символов может
занимать любую позицию, то общее количество
возможных вариантов равно произведению числа
вариантов, полученного для одного «закрепленного»
символа на количество заданных символов.

15.

Глава 5, §18
*
.
Для выделенного случая выпишем возможные
варианты,
используя
схему.
Подсчитаем
полученное число вариантов – их 6.
6 ∙ 3 = 18.
Ответ: 18 завтраков.

16.

Глава 5, §18
*
.
Метод организованного перебора
(подсчет числа комбинаций из различных символов)
1. Закрепить на первом месте комбинации один из символов,
принадлежащих множеству заданных в задаче символов.
2. Для выделенного случая выписать возможные варианты,
используя таблицу, схему или др. Подсчитать полученное число
вариантов.
3. Если по условию задачи каждый из символов может занимать
любую позицию, то общее количество возможных вариантов равно
произведению числа вариантов, полученного для одного
«закрепленного» символа на количество заданных символов.
4. Если на символы наложены какие-либо ограничения, то
вычислить количество возможных вариантов отдельно для всех
символов с различными свойствами, а затем сложить полученные
числа.

17.

Глава 5, §18
*
.
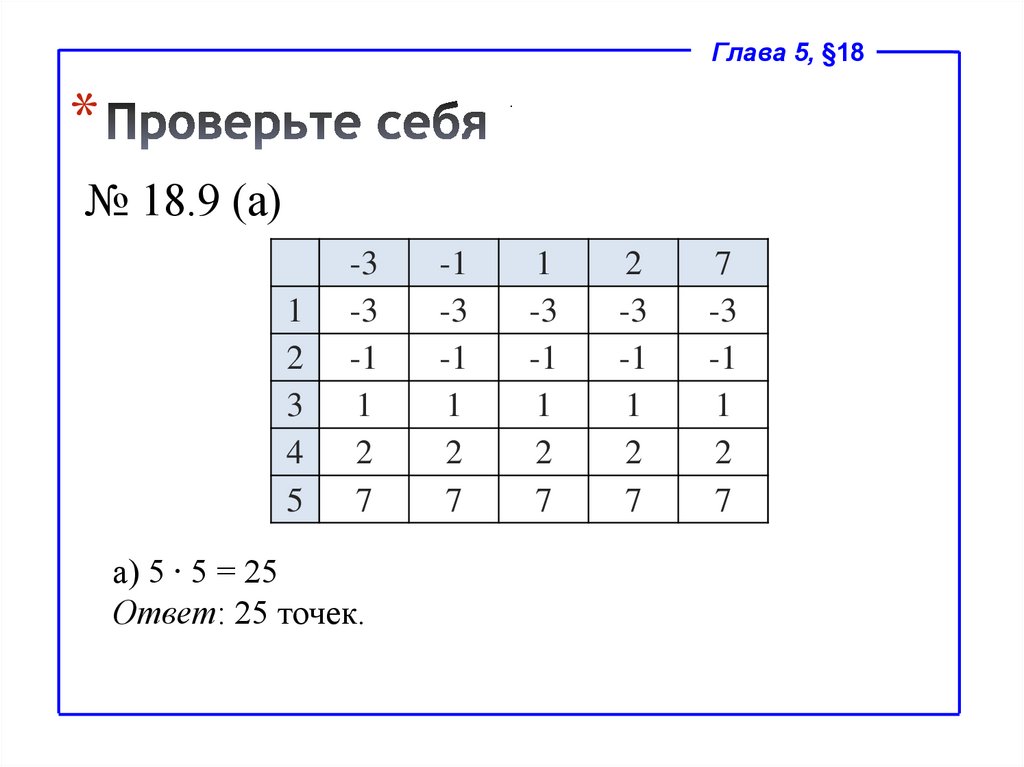
№ 18.9 (а)
1
2
3
4
5
-3
-3
-1
1
2
7
а) 5 ∙ 5 = 25
Ответ: 25 точек.
-1
-3
-1
1
2
7
1
-3
-1
1
2
7
2
-3
-1
1
2
7
7
-3
-1
1
2
7

18.

Глава 5, §18
*
.
1) Определить новые знания, которые открыты на
уроке.
2) Сформулируйте цель, которая стояла перед
вами.
3) Определите, достигнута ли цель.
4) Перечислите средства и способы, которые вам
помогли достичь цели.
5) Оцените деятельность пары и каждого
участника пары на уроке.
6) Сформулируйте неразрешённые затруднения
на уроке, если они есть.