Похожие презентации:
Теорема о трёх перпендикулярах
1. Тема урока
Теорема о трёхперпендикулярах
2. Ответь на вопросы
1.Сформулировать определениеперпендикулярных прямых.
2. Сформулировать определение
прямой,
перпендикулярной к плоскости.
3. Сформулировать признак
перпендикулярности прямой и
плоскости.
4. Рассказать о случаях взаимного
расположения перпендикулярных
прямых.
3. Тест
1. Угол между двумя прямыми равен90?.
Как называются эти прямые?
А) параллельные;
Б) скрещивающиеся;
В) перпендикулярные.
4.
2. Две скрещивающиеся прямыевзаимно перпендикулярны.
Чему равен угол между ними?
А) 0;
Б) 90;
В) 180.
5.
3. Одна из скрещивающихся прямыхперпендикулярна плоскости,
а вторая не пересекает эту плоскость.
Могут ли быть параллельны эти прямые?
А) да;
Б) нет.
6.
4. Прямая а лежит в данной плоскости,прямая в перпендикулярна к этой плоскости
Чему равен угол между этими прямыми?
А) 0°;
Б) 180°;
В) 90°;
Г) нет правильного ответа.
7. Ответы:
1–В2- Б
3–Б
4- В
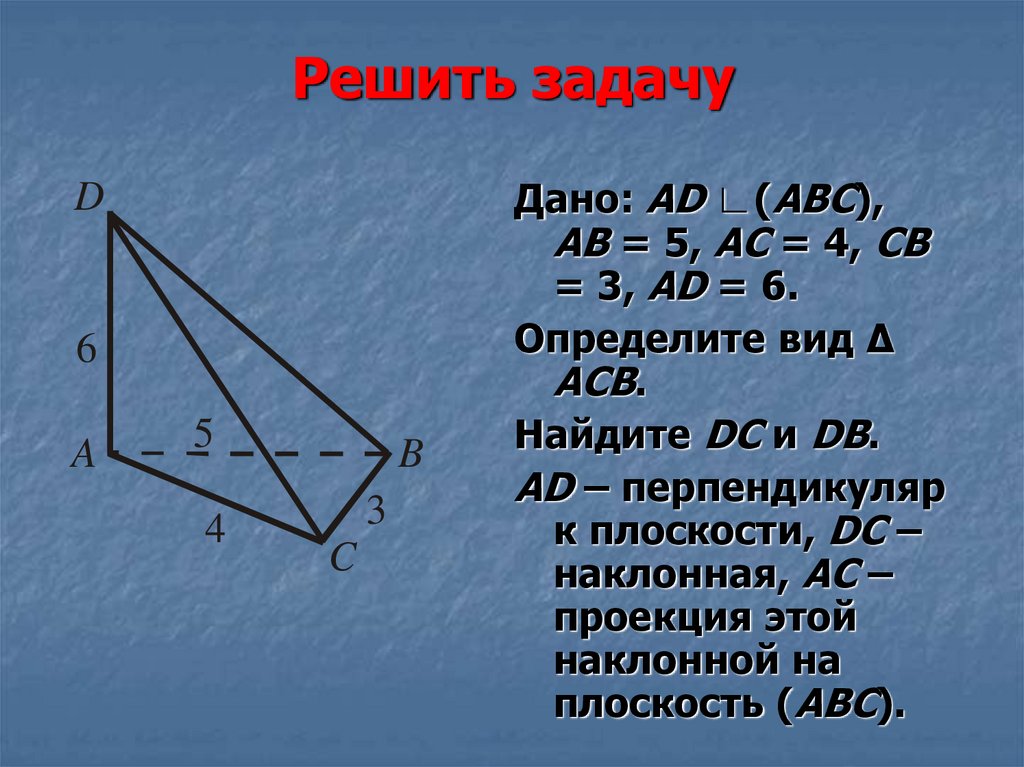
8. Решить задачу
D6
A
5
4
B
3
C
Дано: AD ∟(АВС),
АВ = 5, АС = 4, СВ
= 3, AD = 6.
Определите вид Δ
АСВ.
Найдите DC и DB.
AD – перпендикуляр
к плоскости, DC –
наклонная, AC –
проекция этой
наклонной на
плоскость (АВС).
9.
DB
A
C
Дано:
AD ∟(АВС),
СВ ∟АС
Доказать, что:
а) AD ∟ CB;
б) СВ ∟(ADC);
в) СВ ∟ CD.
10.
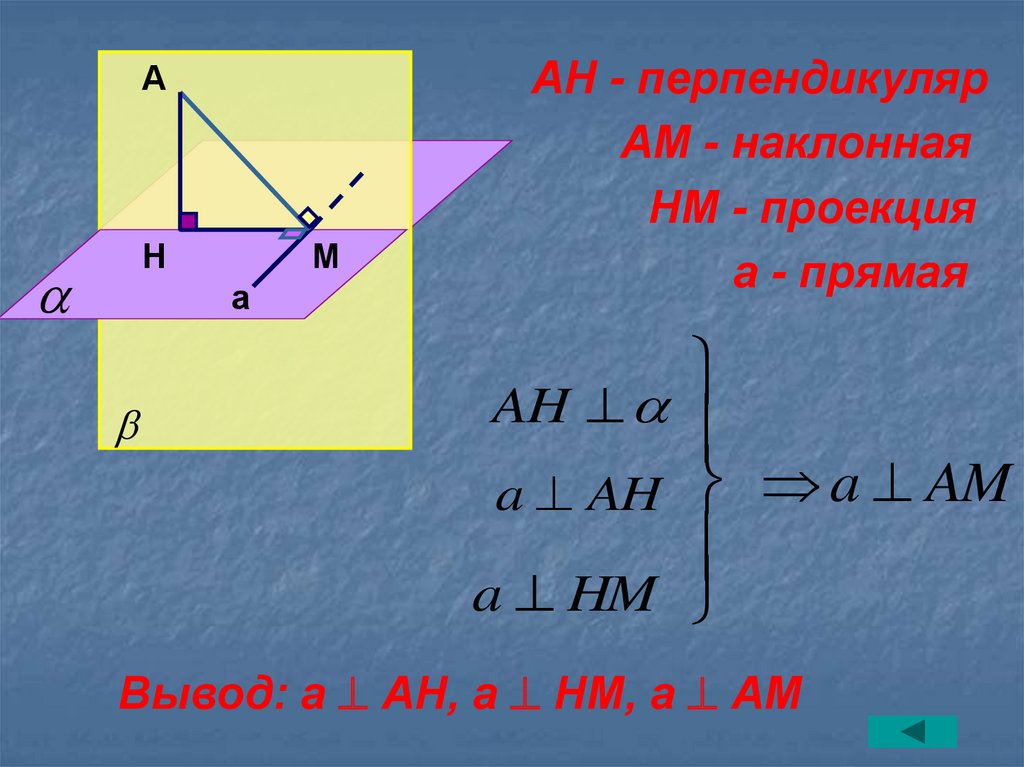
Теоремао трех
перпендикулярах
11.
ТеоремаПрямая, проведенная в
плоскости через основание
наклонной перпендикулярно
к её проекции на эту
плоскость, перпендикулярна
и к самой наклонной.
12.
АН
М
а
AH - перпендикуляр
AM - наклонная
НМ - проекция
а - прямая
AH
a AH
a HM
a AM
Вывод: а АН, а НМ, а АМ
13.
14.
Домашнее задание:теория (п. 20), № 148.
150 – по желанию.













 Математика
Математика








