Упражнения на отработку заданий. График функции y=f(x) и касательная к нему в точке с абсциссой x0=1

1.

Упражнения на отработку заданий
Единого Государственного экзамена по математике
Учитель МБОУ СОШ №2 г. Салехард
Кривокорова Н.Ю.

2.

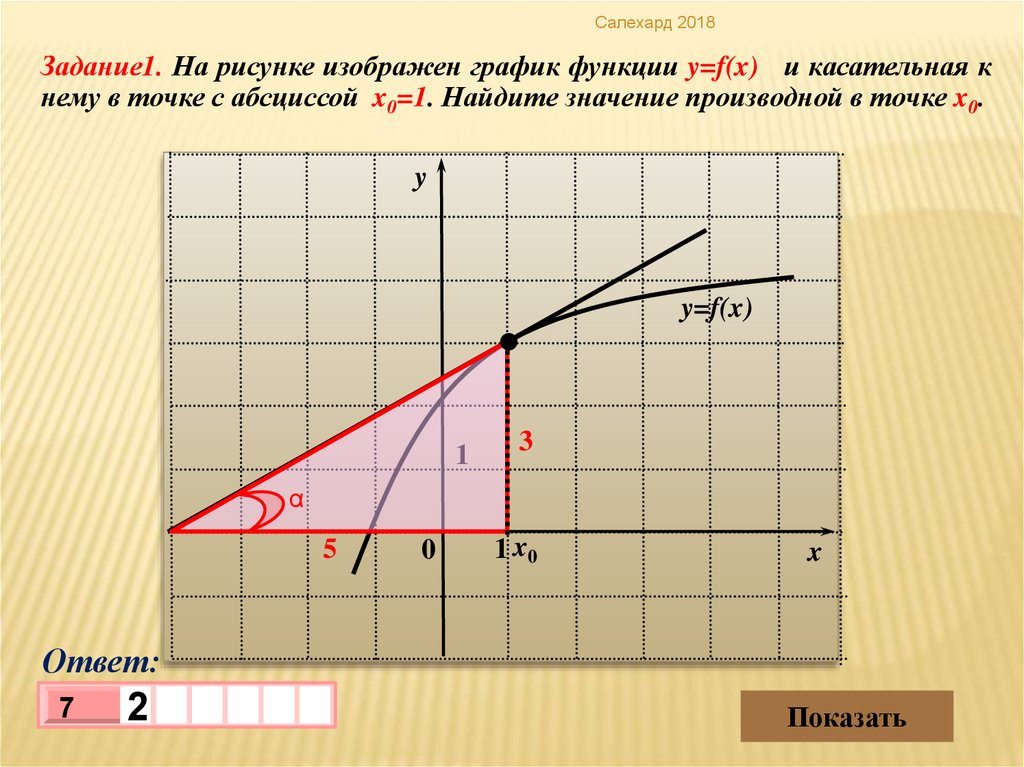
Салехард 2018
Задание1. На рисунке изображен график функции y=f(x) и касательная к
нему в точке с абсциссой x0=1. Найдите значение производной в точке x0.
y
y=f(x)
1
3
α
5
0
1 x0
x
Ответ:
7
2
3
10 х
х
Показать

3.

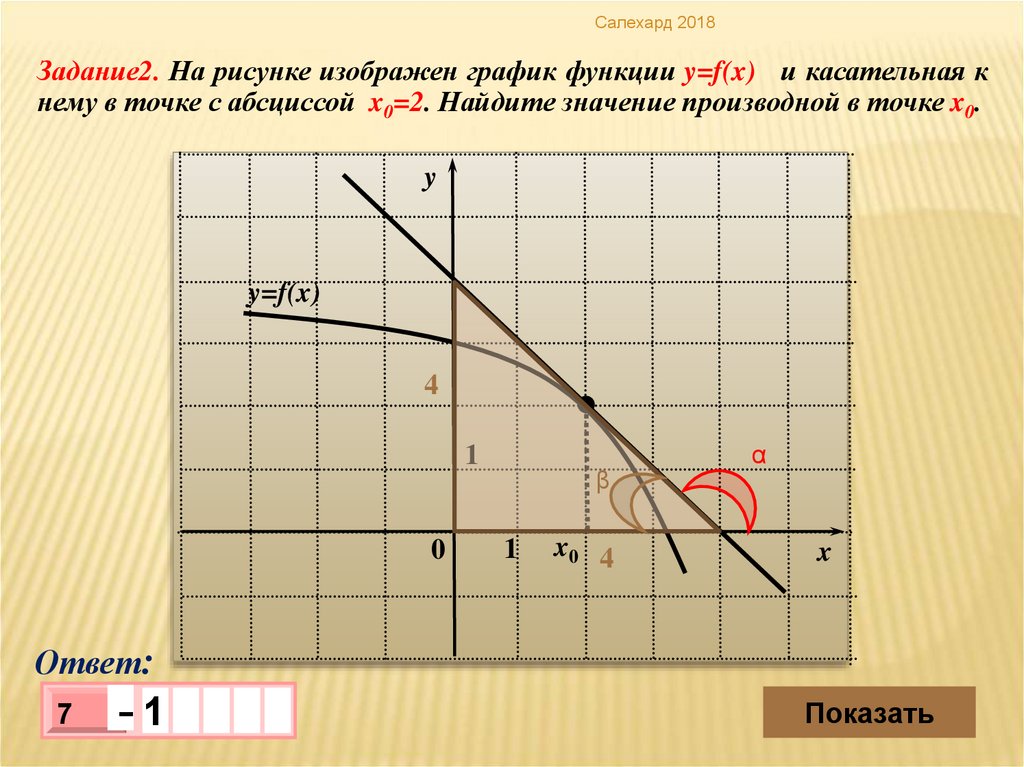
Салехард 2018
Задание2. На рисунке изображен график функции y=f(x) и касательная к
нему в точке с абсциссой x0=2. Найдите значение производной в точке x0.
y
y=f(x)
4
1
0
β
1
x0 4
α
x
Ответ:
7
-1
3
10 х
х
Показать

4.

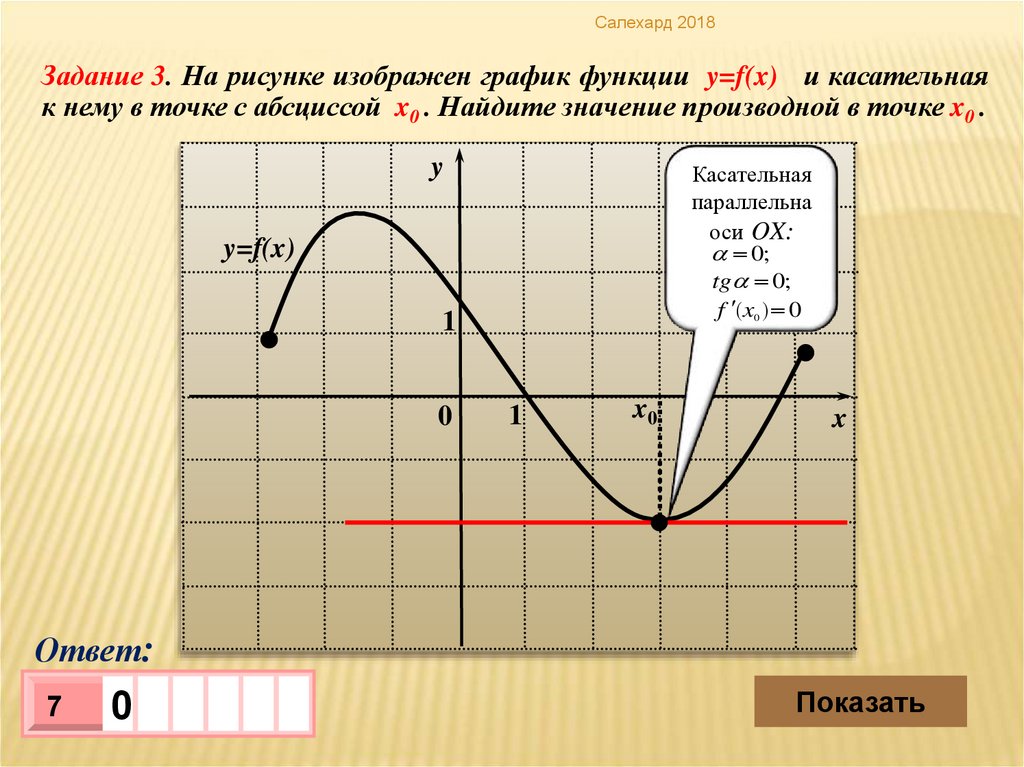
Салехард 2018
Задание 3. На рисунке изображен график функции y=f(x) и касательная
к нему в точке с абсциссой x0 . Найдите значение производной в точке x0 .
y
Касательная
параллельна
оси OX:
0;
tg 0;
f x0 0
y=f(x)
1
0
1
x0
x
Ответ:
7
0
3
10 х
х
Показать

5.

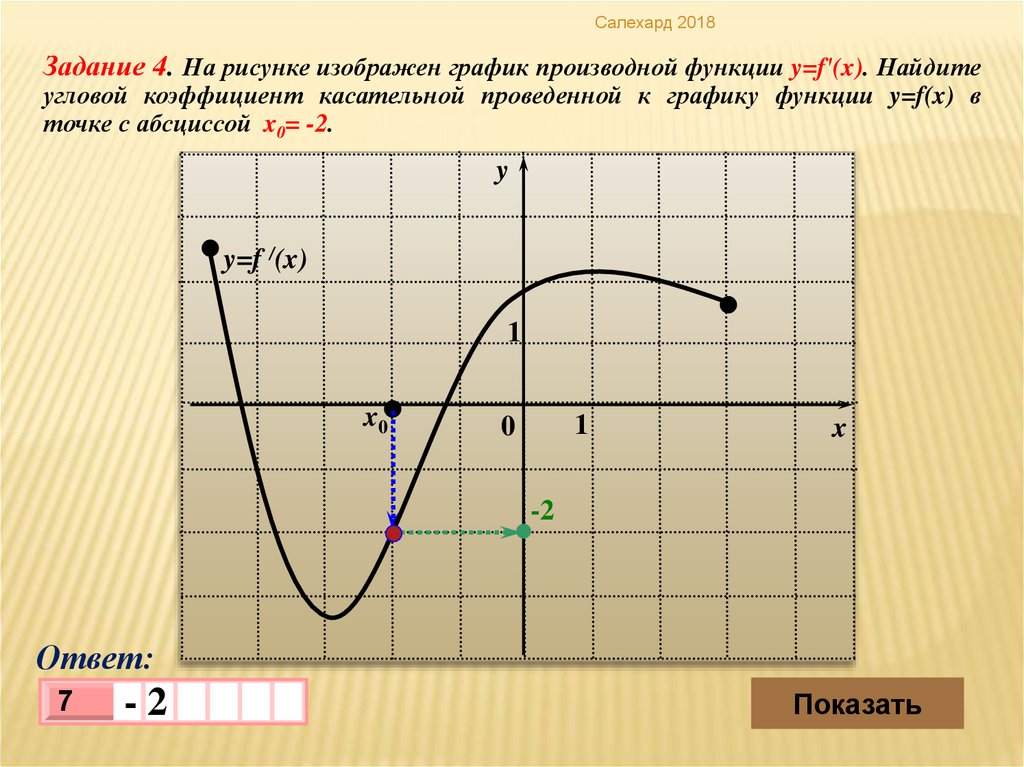
Салехард 2018
Задание 4. На рисунке изображен график производной функции y=f′(x). Найдите
угловой коэффициент касательной проведенной к графику функции y=f(x) в
точке с абсциссой x0= -2.
y
y=f /(x)
1
x0
1
0
x
-2
Ответ:
7
-2
3
10 х
х
Показать

6.

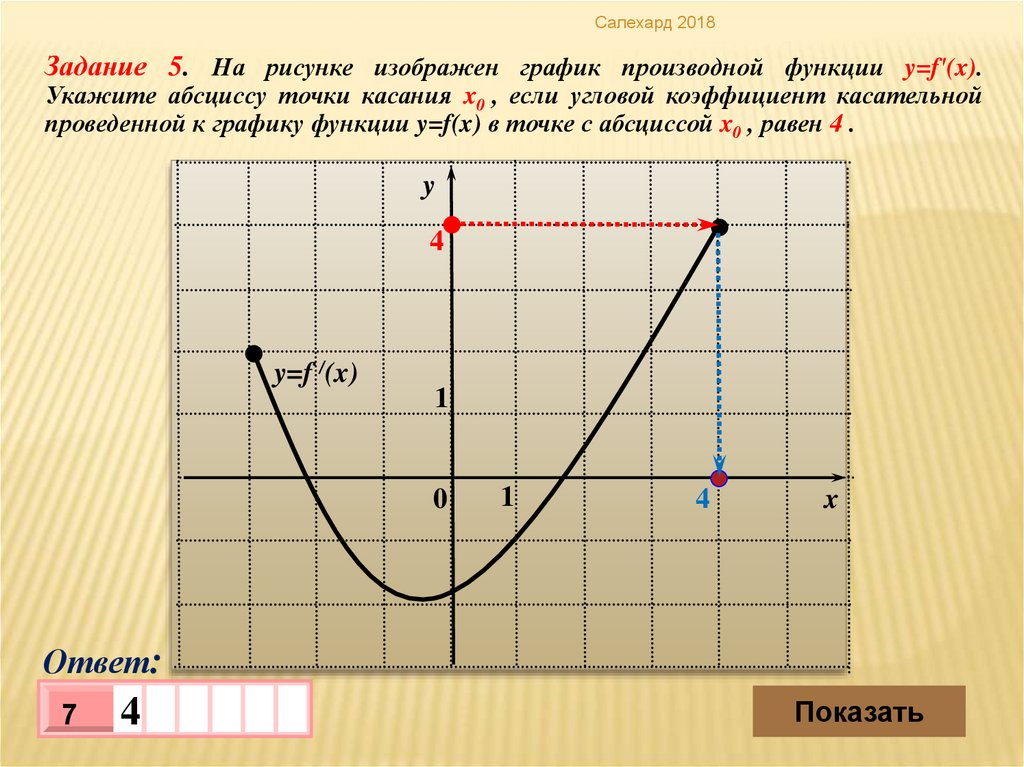
Салехард 2018
Задание 5. На рисунке изображен график производной функции y=f′(x).
Укажите абсциссу точки касания x0 , если угловой коэффициент касательной
проведенной к графику функции y=f(x) в точке с абсциссой x0 , равен 4 .
y
4
y=f /(x)
1
0
1
4
x
Ответ:
7
4
3
10 х
х
Показать

7.

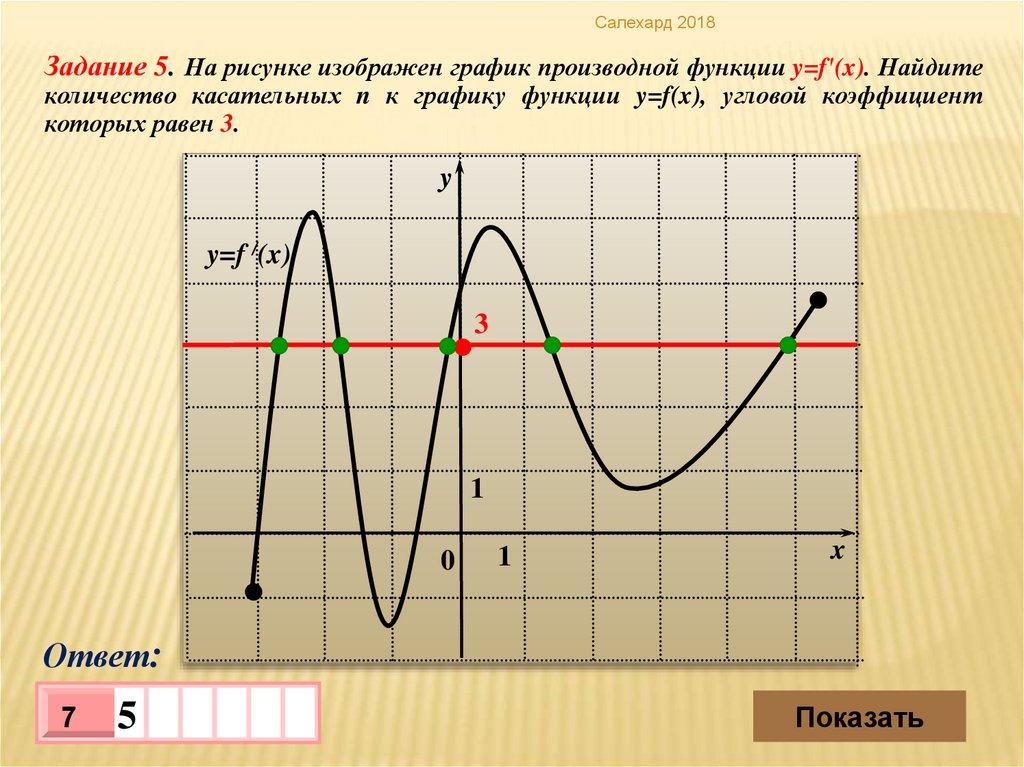
Салехард 2018
Задание 5. На рисунке изображен график производной функции y=f′(x). Найдите
количество касательных n к графику функции y=f(x), угловой коэффициент
которых равен 3.
y
y=f /(x)
3
1
0
1
x
Ответ:
7
5
3
10 х
х
Показать

8.

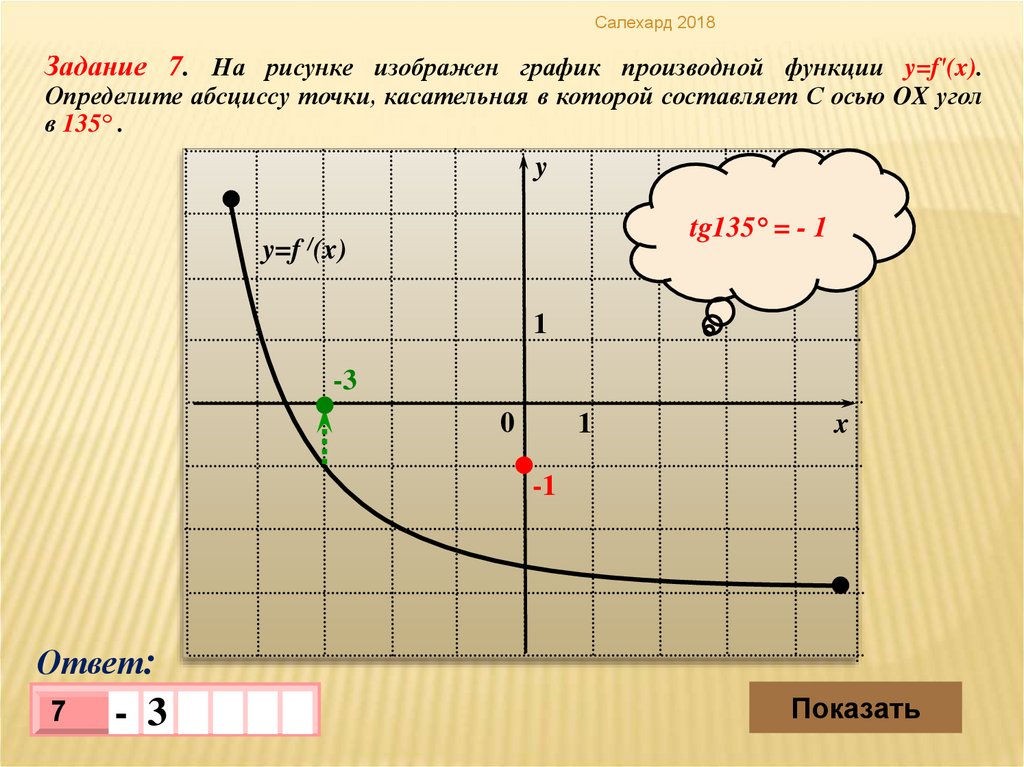
Салехард 2018
Задание 7. На рисунке изображен график производной функции y=f′(x).
Определите абсциссу точки, касательная в которой составляет С осью OX угол
в 135° .
y
y=f
tg135° = - 1
/(x)
1
-3
0
1
x
-1
Ответ:
7
- 3
3
10 х
х
Показать

9.

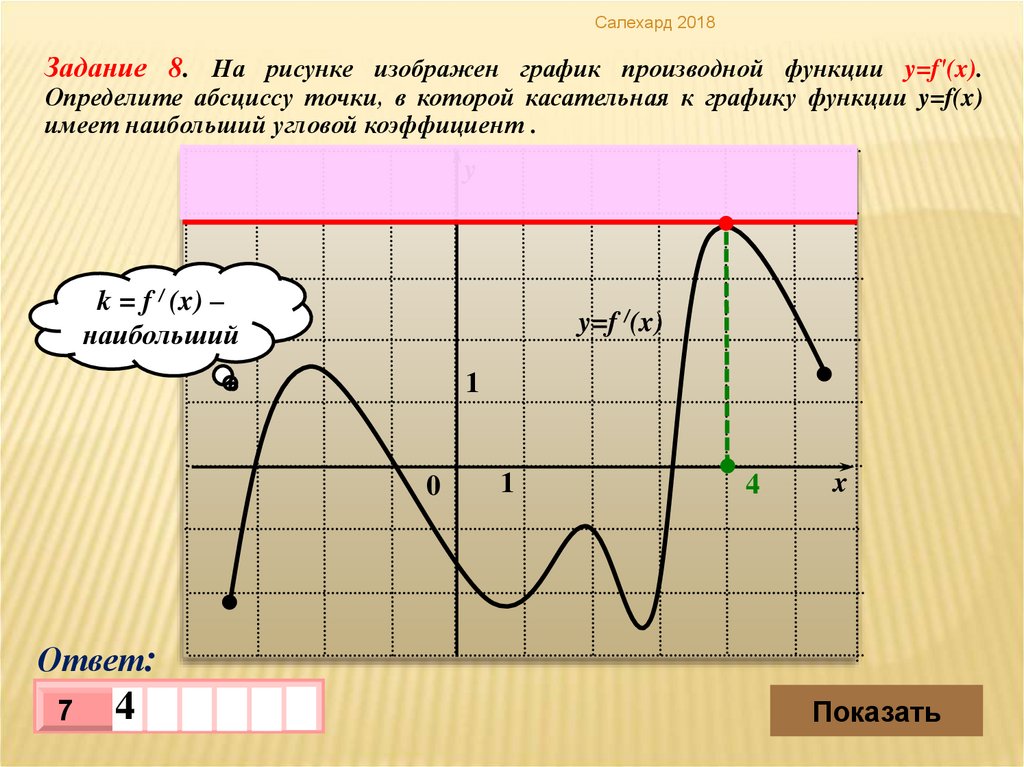
Салехард 2018
Задание 8. На рисунке изображен график производной функции y=f′(x).
Определите абсциссу точки, в которой касательная к графику функции y=f(x)
имеет наибольший угловой коэффициент .
y
k = f / (x) –
наибольший
y=f /(x)
1
0
1
4
x
Ответ:
7
4
3
10 х
х
Показать

10.

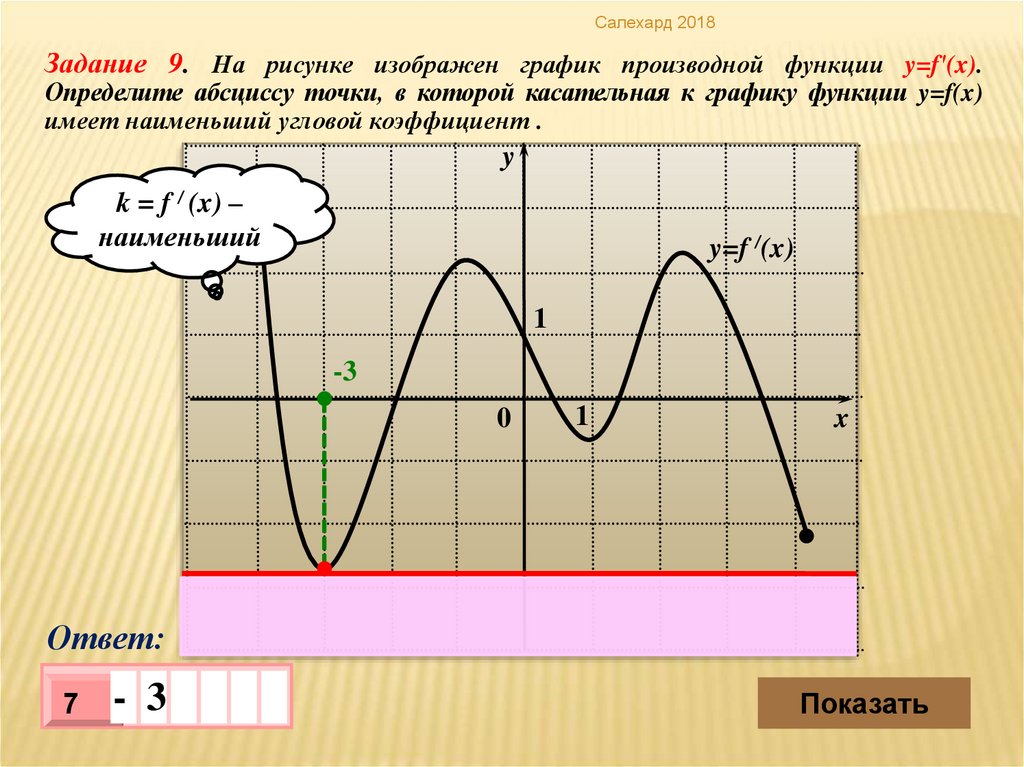
Салехард 2018
Задание 9. На рисунке изображен график производной функции y=f′(x).
Определите абсциссу точки, в которой касательная к графику функции y=f(x)
имеет наименьший угловой коэффициент .
y
k = f / (x) –
наименьший
y=f /(x)
1
-3
0
1
x
Ответ:
7
- 3
3
10 х
х
Показать