Похожие презентации:
Касательная к графику функции
1. Касательная к графику функции
2.
График - прямаяЛинейная функция: y= k x + b
k - угловой коэффициент прямой
Уравнение прямой с угловым
коэффициентом
3.
k = tg αПрямая, проходящая через точку (хо; f(хо)), с
угловым коэффициентом f `(xo)
4.
Если в точке xo существуетпроизводная, то существует и
касательная (невертикальная) к
графику функции в точке xo.
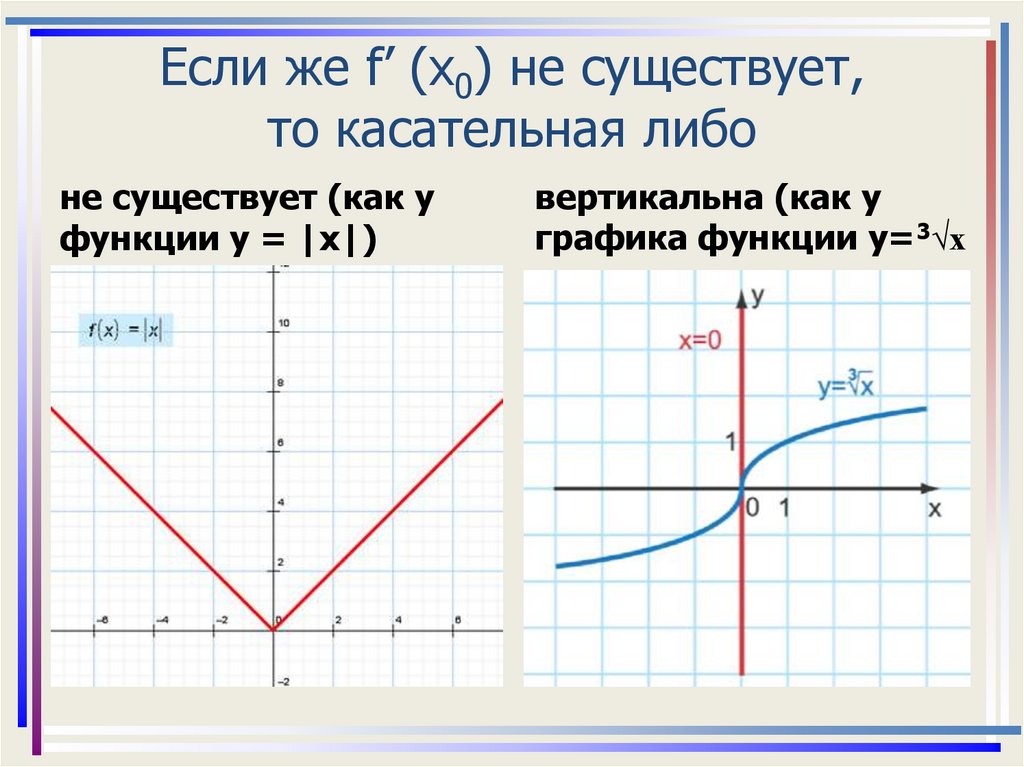
5. Если же f’ (x0) не существует, то касательная либо
не существует (как уфункции у = |х|)
вертикальна (как у
графика функции у=3√х
6.
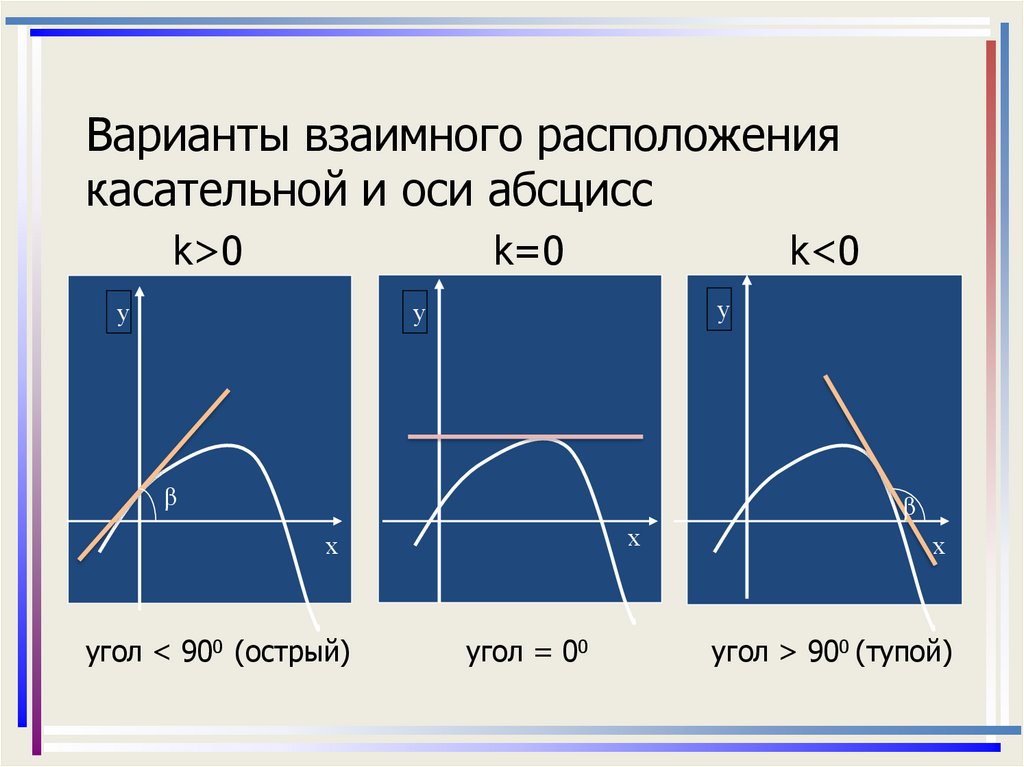
Варианты взаимного расположениякасательной и оси абсцисс
k>0
k=0
у
k<0
у
у
β
β
х
х
угол < 900 (острый)
угол = 00
х
угол > 900 (тупой)
7.
Геометрический смысл производной:Угловой коэффициент касательной равен
значению производной функции в точке
проведения касательной
k = f `(xo)
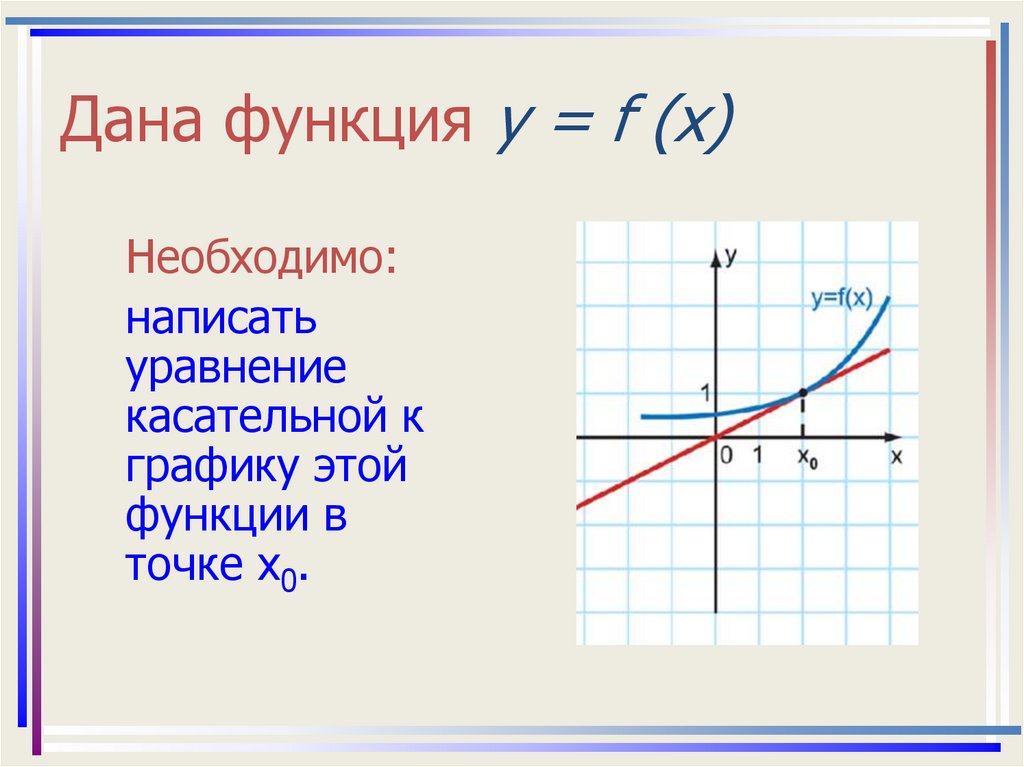
8. Дана функция у = f (x)
Необходимо:написать
уравнение
касательной к
графику этой
функции в
точке х0.
9. Вывод:
Уравнение касательнойимеет вид:
y = f(xo) + f `(xo)( x – xo)
10. Алгоритм
• Найти значение функции в точке хо• Вычислить производную функции
• Найти значение производной функции в
точке хо
• Подставить полученные числа в формулу
y = f(xo) + f `(xo)( x – xo)
• Привести уравнение к стандартному
виду
11. Дана функция у = х3
3Дана функция у = х
• Необходимо:
написать уравнение
касательной к графику этой
функции в точке х0 = 1.
Уравнение касательной
у = 3х - 2
12. Задание:
На параболе у = 3х2 - 4х + 6• найти точку, в которой
касательная к ней // прямой
у =2х+4,
• написать уравнение
касательной в этой точке.
13. Задание:
На параболе у = х2 + 5х – 16 найтиточку, в которой касательная к ней //
прямой 5х+у+4 =0 и написать
уравнение касательной в этой точке.










 Математика
Математика








