Похожие презентации:
Итоговое повторение. Решение рациональных и иррациональных уравнений. 9 класс
1. Урок математики в 9 классе
28.12.2023Урок математики в 9 классе
«Мне приходится делить свое время
между политикой и уравнениями.
Однако уравнения, по-моему, гораздо
важнее, потому что политика
существует только для данного
момента, а уравнения будут
существовать вечно».
А.Эйнштейн
2. Тема урока: Итоговое повторение. Решение рациональных и иррациональных уравнений
28.12.2023Тема урока:
Итоговое повторение.
Решение рациональных
и иррациональных
уравнений
3.
− 5х4 − 4х2 − 6 = 06у − 8 = 10
Линейное
Квадратное
2x 3 4x 1 4
Дробно - рациональное
Биквадратное
6х2 − 2х = 33
6
2х
1
х х 1
Какое уравнение осталось?
4. Мозговой штурм
Какое уравнение называется иррациональным?Уравнения, в которых переменная содержится
под знаком корня, называются
иррациональными.
Устно: какие из следующих уравнений
являются иррациональными?
а) х + √ х = 2
д) х + √ х = 0
б) х √7 = 11+х
е) у² - 3 √ 2 = 4
в)у + √ у²+9 = 2
г)√ х – 1 = 3
Какое уравнение не имеет корней?
5. Найди ошибку
16 – 36 = 25 – 4516 – 36 + 20,25 = 25 – 45 + 20,25
4² - 2 ∙ 4 ∙ 4,5 + 4,5² = 5 ² -2 ∙ 5 ∙ 4,5 +4,5²
(4 - 4,5)² = (5 - 4,5)²
4 - 4,5 = 5 - 4,5
4=5
6.
Основные методы решения иррациональныхуравнений:
Графический метод;
Метод возведения обеих частей уравнения в
одну и ту же степень с последующей проверкой;
Метод возведения обеих частей уравнения в одну
и ту же степень с использованием ОДЗ.
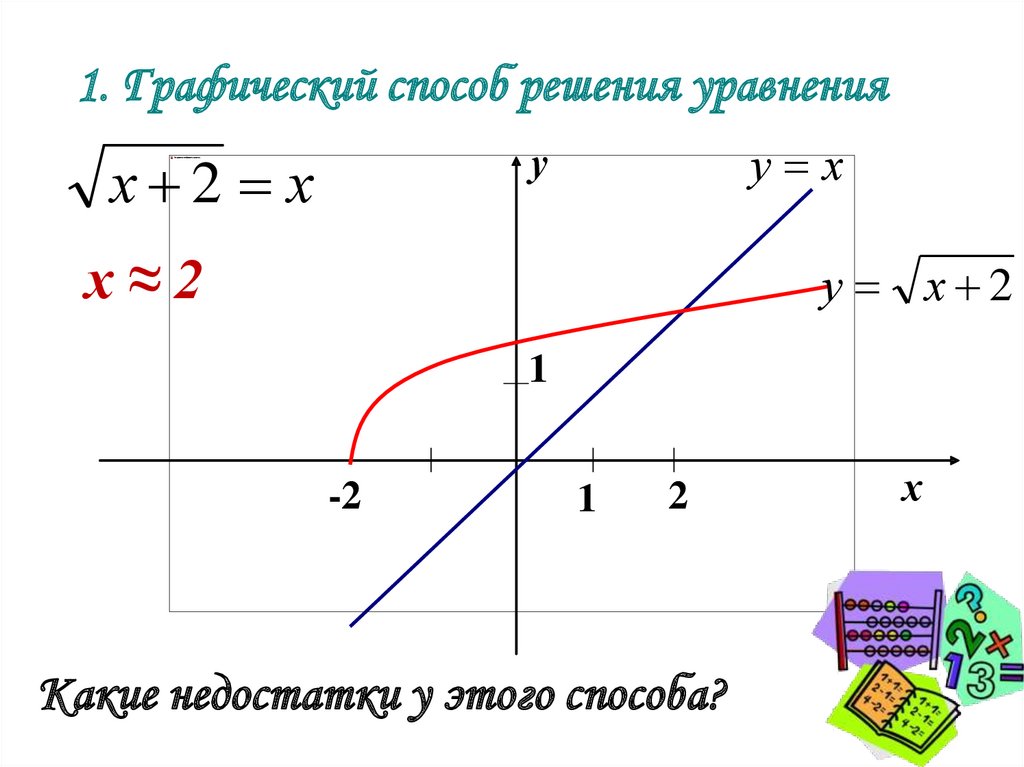
7. 1. Графический способ решения уравнения
у ху
х 2 х
х≈2
у х 2
1
-2
1
2
Какие недостатки у этого способа?
х
8. 2. Метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой
2 x х2
а) х 1
( 2 х ) х
2 2
2
2 12 1
1 1 − верно
2 х х
− корень уравнения
2
х
1
2 х 2
б ) х 1
2
х 1
2 ( 1) 2 1
х 1илих 1 1 1 − неверно
2
Ответ: 1
2
х 1
− посторонний
корень
9. 3. Метод возведения обеих частей уравнения в одну и ту же степень с использованием ОДЗ
2 x х2
1. х ≥ 0
2 2
2
2.( 2 х ) х
2 х х
2
х 1
х 1или х 1
Ответ: 1
2
2
не удовл. условию
10.
Древнегреческий ученыйисследователь,который впервые доказал
существование иррациональных
чисел
11.
1. Какой этап является
обязательным при решении
иррациональных уравнений?
проверка
2. Способ, с помощью
которого выполняется
подстановка
проверка решения
иррационального уравнения.
3. Как называется знак
радикал
корня?
4. Сколько решений имеет
ноль
2
уравнение х =а, если а<0?
5. Как называются
иррациональные
уравнения, в которых под
знаком корня содержится
переменная?
квадратный
6. Как называется корень
второй степени?
12.
ЕВКЛИДПознание мира ведет к
совершенствованию
души
13.
√х+2=хРешение:
х + 2 = х2,
х2 – х – 2 = 0
х1 = 2 и х 2 =
-1
• При х = 2, 2=2, верно.
• При х = -1, 1= -1, ложно
Ответ:
2
14.
Решаем уравнения из ОБЗ ОГЭ15. Тренировка
• Стр. 179 № 4616. Дома:
стр. 179№ 49, 51
17. Продолжите фразу
Сегодня на уроке я узналСегодня на уроке я научился
Сегодня на уроке я
познакомился
Сегодня на уроке я повторил
Сегодня на уроке я закрепил
18.
Желаю, чтобы Вашивозможности пополнялись по
мере изучения математики, а на
экзамене вы смогли бы
подобрать «ключи» к решению
любого уравнения.

















 Математика
Математика








