Решение иррациональных уравнений

1.

Тема урока:
Решение
иррациональных
уравнений

2.

Содержание
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Эпиграф.
Виды уравнений.
Определение иррациональных уравнений.
Упражнения на распознавание видов уравнений.
Работаем устно.
Методы решения.
Графический метод.
Функционально-графический метод.
Решите уравнения.
Возведение в степень (алгоритм 1).
Алгоритм 2.
Пример по алгоритму 1.
Пример по алгоритму 2.
Специальные методы решения уравнений.
Справка по ОДЗ.
Справка. Корень n-й степени.
Справка. Модуль.
Об авторе.

3.

Именно математика
дает надежнейшие правила:
кто им следует – тому
не опасен обман чувств.
Л. Эйлер

4. Виды уравнений

Целые уравнения
Дробно-рациональные
Иррациональные
Тригонометрические
Показательные
Логарифмические

5.

Определение
Иррациональное уравнение –
уравнение, содержащее
переменную под знаком
корня (радикала).
(примеры)
(справка)

6.

Какие из данных уравнений
являются иррациональными?
x
2
3x 4
2 1
1.
2.
3x 3 7 0
x 1 x 3
3.
4.
2
x
x
2

7.

Работаем устно
1)
3
x 1 2;
2)
3)
x 2;
3
x 0;
7) x 2 2 ;
8) 5 x 25;
4
2
4) 2 x 0;
9) x 2 x 3 2;
x 1
10) 2 x 0,01 0.
5)
4
6) 8 2 x 1

8.

Методы решения
Графический
Основные
алгебраические
Специальные
(Функциональнографический)
• Возведение
обеих частей
уравнения в
степень
(подробнее)
• Переход к
равносильной
системе
(подробнее)

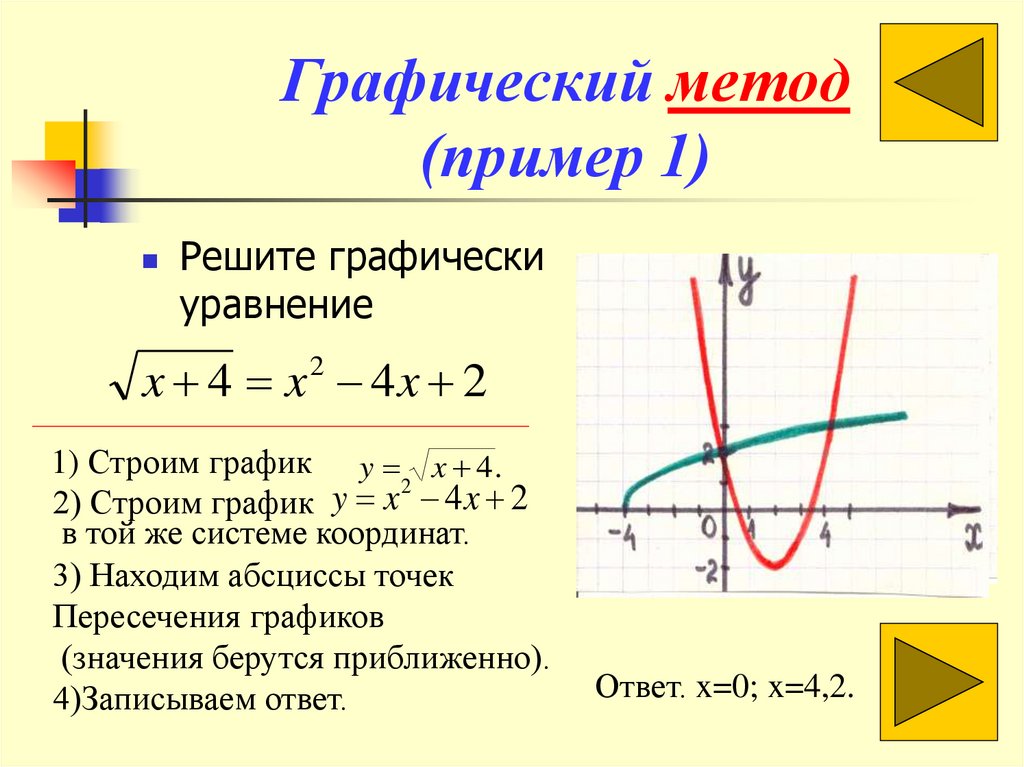
9. Графический метод (пример 1)

Решите графически
уравнение
x 4 x2 4x 2
1) Строим график y x 4 .
2
y
x
4x 2
2) Строим график
в той же системе координат.
3) Находим абсциссы точек
Пересечения графиков
(значения берутся приближенно).
4)Записываем ответ.
Ответ. x=0; x=4,2.

10.

Функционально-графический
метод
x 7 5 x
Пример: решите уравнение
Решение.
x 7 - возрастает на D(f).
1. f(x)=
2. g(x)=5-x, убывает на D(g).
3. Уравнение f(x)=g(x) имеет не более одного
корня.
4. Подбором находим, что X=2.
Ответ. 2.

11.

Решите уравнения
1)
2)
3
3x 1 x 1,
(алгоритм 2)
3 3x x 1.
(алгоритм 1)
3) x 2x 10 2x 1
2
(алгоритм)

12. Алгоритм 1

При n – четном
1.
2.
3.
4.
5.
6.
Уедини корень (если необходимо);
Возведи обе части уравнения в степень n;
Если необходимо, то выполни п.1;
Реши полученное уравнение;
Выполни проверку!
Запиши ответ.
(к методам)

13.

Алгоритм 2
При n - нечетном
1.
2.
3.
4.
5.
Уедини корень (если необходимо);
Возведи обе части уравнения в степень n;
Если необходимо, то выполни п.1;
Реши полученное уравнение;
Запиши ответ.
(к методам)

14. Возведение в степень

*
3 3x x 1
Решение. Возведем обе части уравнения в квадрат:
3 3x x 2 x 1
2
Преобразуем:
Проверка.
x x 2 0
x 1, x 2
2
Если x=1, то в левой части 0, в правой части 0,
0=0 (верно).
Если x=-2, то в левой части 3, в правой части -3,
3 не равно -3, значит, -2 не является корнем.
Ответ. 1.

15.

Возведение в степень
*
3
3x 1 x 1
Решение.
Возведем обе части уравнения
в 3-ю степень:
3x 1 x 3 3x 2 3x 1
Преобразуем:
x 3 3x 2 0
x x 3 0
x 0 или x 3
2
Ответ. 0 ; 3.

16.

Переход к равносильной
системе
1. Определить условия (если n –четно), при
которых обе части уравнения неотрицательны;
2. Возвести обе части уравнения в n-ю степень;
3. Составить систему из уравнения и неравенства;
4. Решить систему;
5. Записать ответ.
Определение.
2n
f ( x) g ( x), что 1) g ( x) 0,
2n
2) g ( x) f ( x).

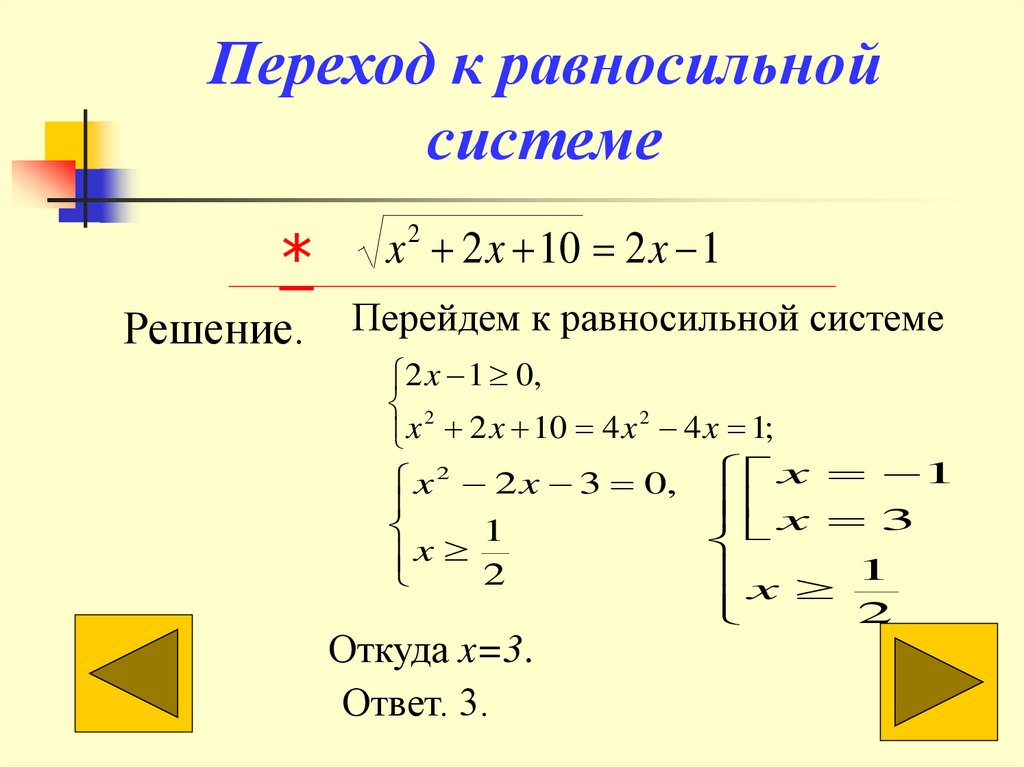
17.

Переход к равносильной
системе
*
Решение.
x 2 x 10 2 x 1
2
Перейдем к равносильной системе
2 x 1 0,
2
2
x
2
x
10
4
x
4 x 1;
x 2 2 x 3 0, x 1
x 3
1
x
1
2
x
2
Откуда x=3.
Ответ. 3.

18. Специальные методы решения

Метод пристального взгляда (справка)
(справка)
Найди ОДЗ
Выполни замену
Умножай на сопряженное
(справка)
Переходи к модулю
Оцени обе части уравнения

19.

Область определения
уравнения (ОДЗ) –
это все значения переменной, при
которых данное уравнение имеет смысл.
Замечание. Если ОДЗ уравнения есть
пустое множество, то говорят, что
данное уравнение не определено на
множестве R и решений заведомо быть
не может.

20.

Справка
•Корень n-й степени из а (
n
это такое число b, что b a
n
а)
-
• Арифметический корень n-й степени:
n
a b, что 1) b 0, 2) b a.
n
n
a n a, n нечетно,
n
a n a , n четно,
n
a
n
a, n любое.

21.

Справка
Модуль числа:
|a| =
а , если a 0,
0, если a 0,
a , если a 0.
Расстояние от 0 до точки, изображающей a на
числовой оси

22. Спасибо за урок!

Успехов в изучении темы!