ГИА. Открытый банк заданий по математике

1.

ГИА
Открытый банк заданий
по математике.

2.

Вашему вниманию представлены тридцать шесть
прототипов задач по геометрии
Открытого банка заданий по математике. ГИА.
Прямоугольный треугольник.
Равносторонний треугольник.
Равнобедренный треугольник.
Произвольный треугольник.
Прямоугольник.
Ромб.
Параллелограмм.
Трапеция.
Круг. Круговой сектор.

3.

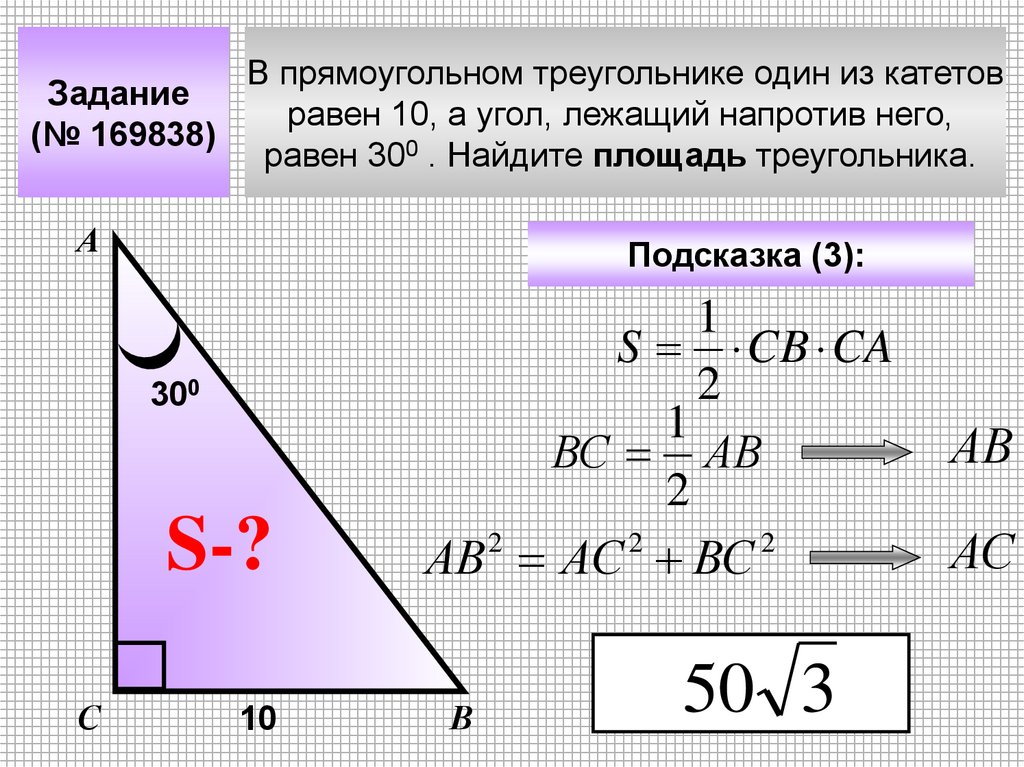
Задание
(№ 169838)
В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него,
равен 300 . Найдите площадь треугольника.
А
Подсказка (3):
300
S-?
С
10
1
S CB CA
2
1
ВС АВ
2
2
2
2
АВ АС ВС
В
50 3
АВ
АС

4.

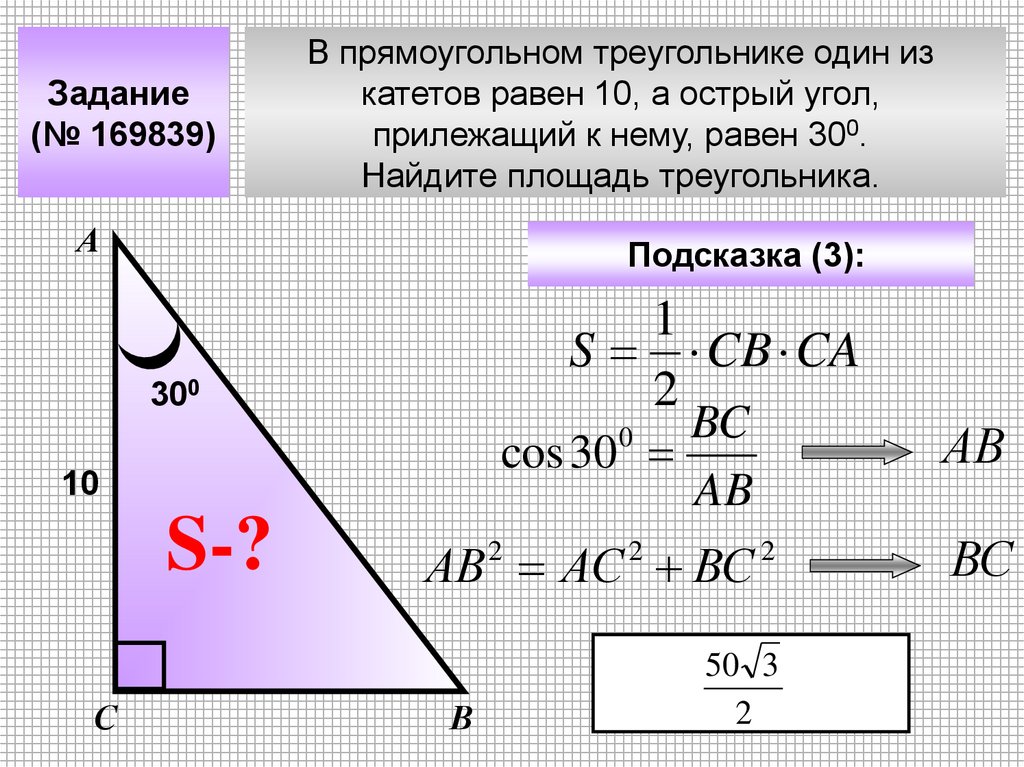
Задание
(№ 169839)
В прямоугольном треугольнике один из
катетов равен 10, а острый угол,
прилежащий к нему, равен 300.
Найдите площадь треугольника.
А
Подсказка (3):
10
1
S CB CA
2
BC
0
cos 30
AB
300
S-?
С
АВ АС ВС
2
В
2
2
50 3
2
АВ
ВС

5.

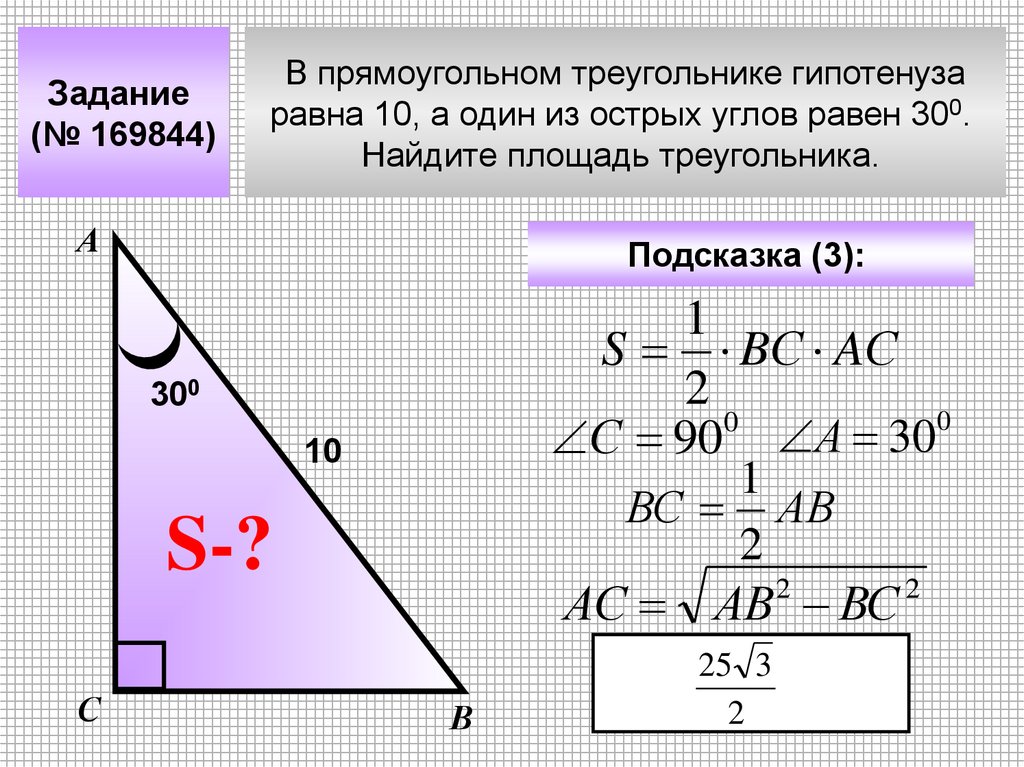
Задание
(№ 169844)
В прямоугольном треугольнике гипотенуза
равна 10, а один из острых углов равен 300.
Найдите площадь треугольника.
А
Подсказка (3):
1
S BС AС
2
0
0
С 90 А 30
300
10
1
ВС АВ
2
АС АВ2 ВС 2
S-?
С
В
25 3
2

6.

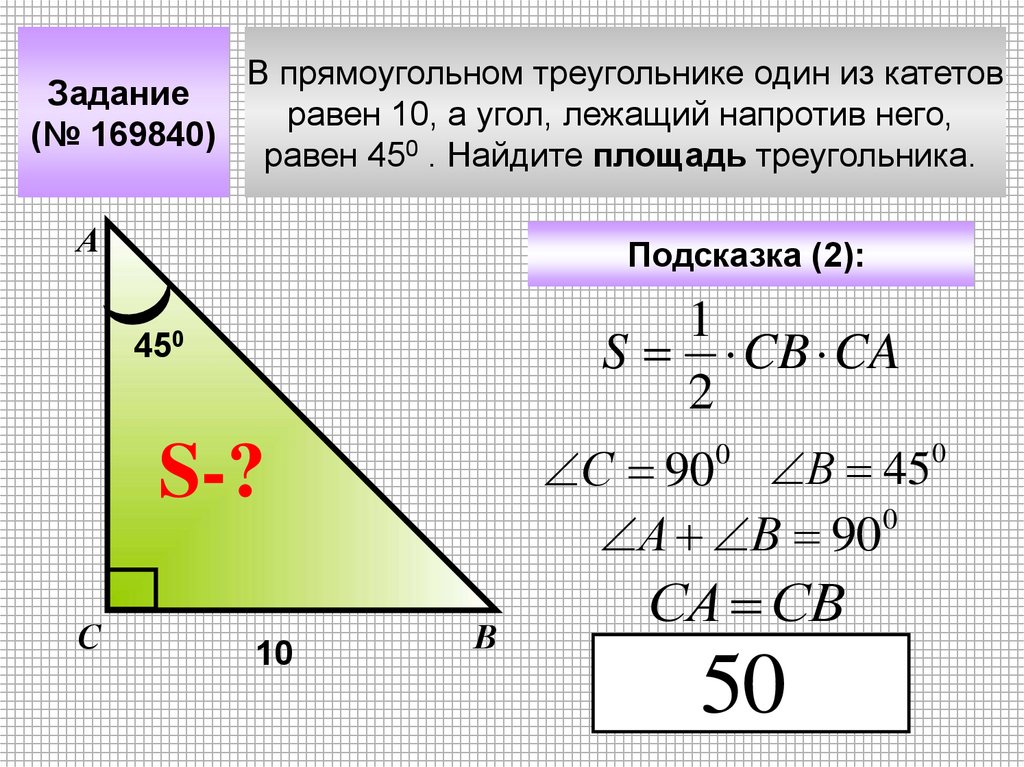
Задание
(№ 169840)
В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него,
равен 450 . Найдите площадь треугольника.
А
Подсказка (2):
1
S CB CA
2
450
С 90 В 45
0
А В 90
0
S-?
С
10
В
СА СВ
50
0

7.

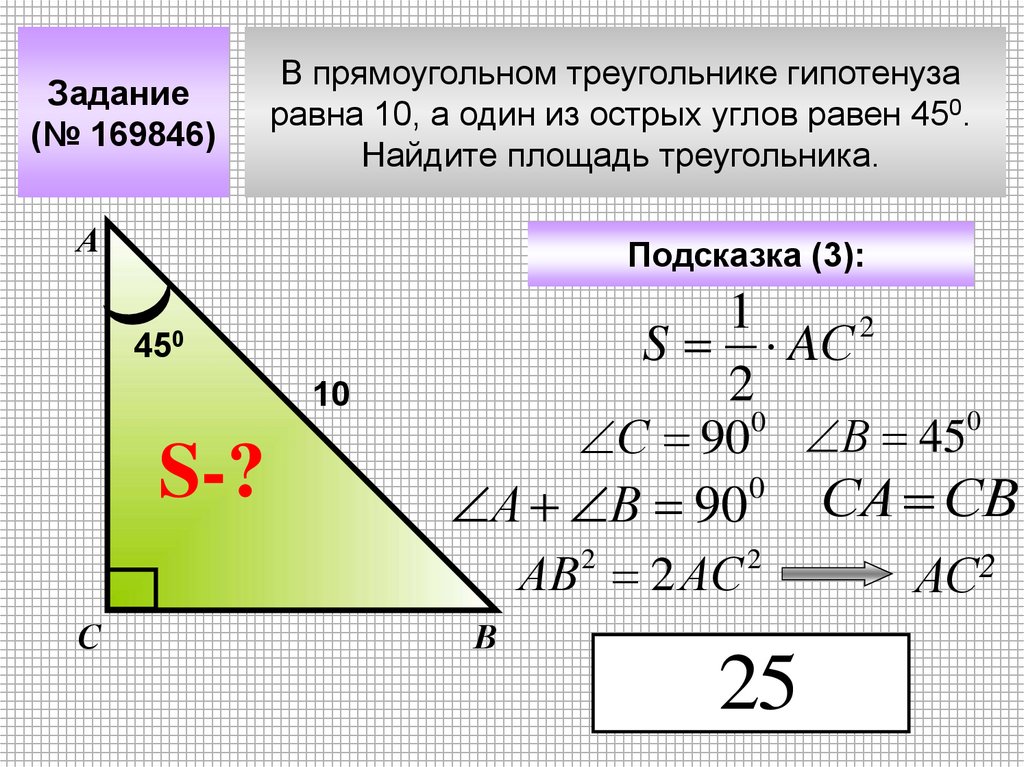
Задание
(№ 169846)
В прямоугольном треугольнике гипотенуза
равна 10, а один из острых углов равен 450.
Найдите площадь треугольника.
А
Подсказка (3):
1
2
S AС
2
450
10
S-?
С 90
А В 90
АВ 2АС
2
С
В
0
0
2
25
В 45
0
СА СВ
АС2

8.

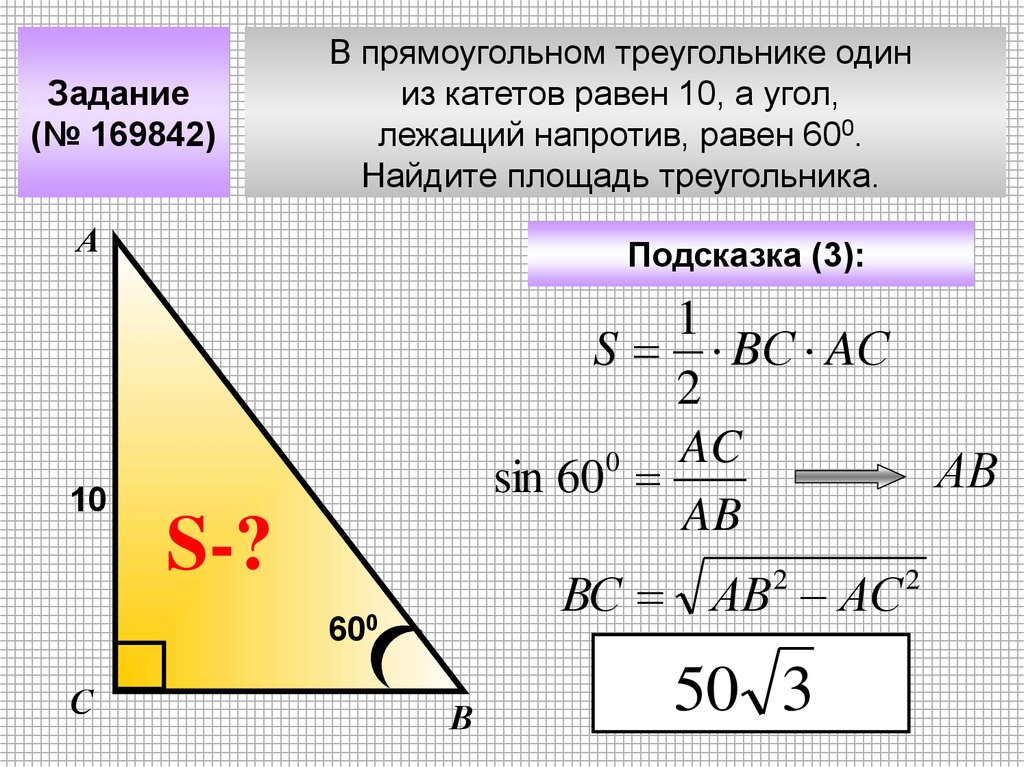
Задание
(№ 169842)
В прямоугольном треугольнике один
из катетов равен 10, а угол,
лежащий напротив, равен 600.
Найдите площадь треугольника.
А
10
Подсказка (3):
1
S BС AС
2
AC
0
АВ
sin 60
AB
S-?
ВС АВ АС
2
600
С
В
50 3
2

9.

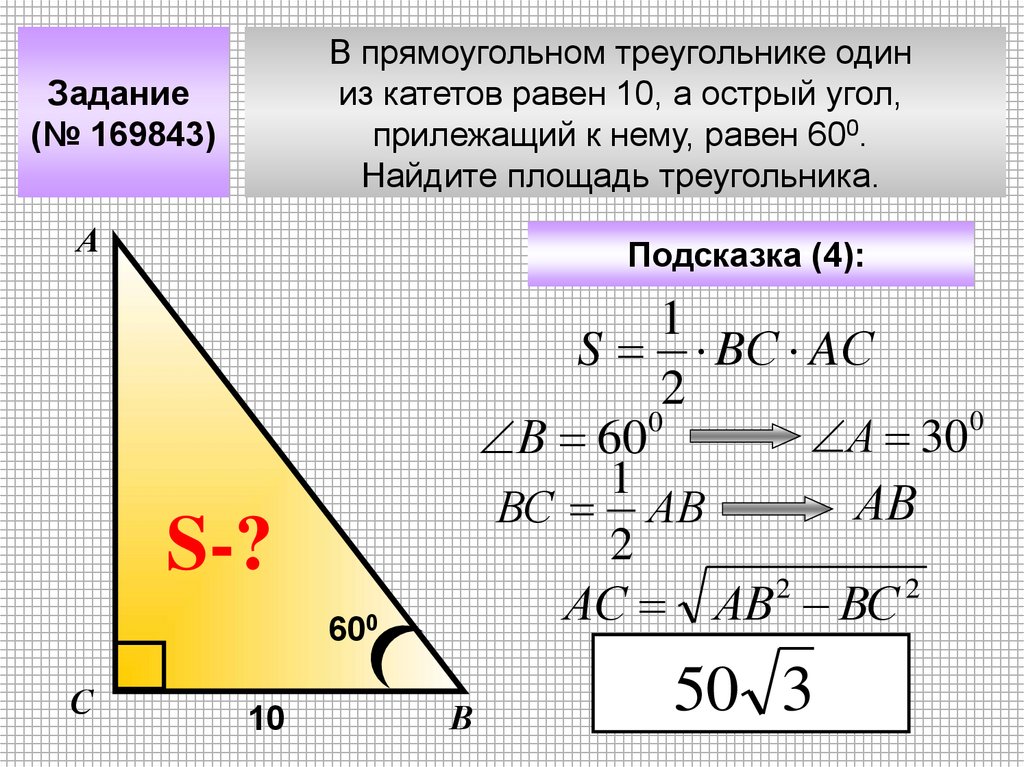
В прямоугольном треугольнике один
из катетов равен 10, а острый угол,
прилежащий к нему, равен 600.
Найдите площадь треугольника.
Задание
(№ 169843)
А
Подсказка (4):
1
S BС AС
2
0
0
А 30
В 60
1
АВ
ВС АВ
S-?
2
АС АВ2 ВС 2
600
С
10
В
50 3

10.

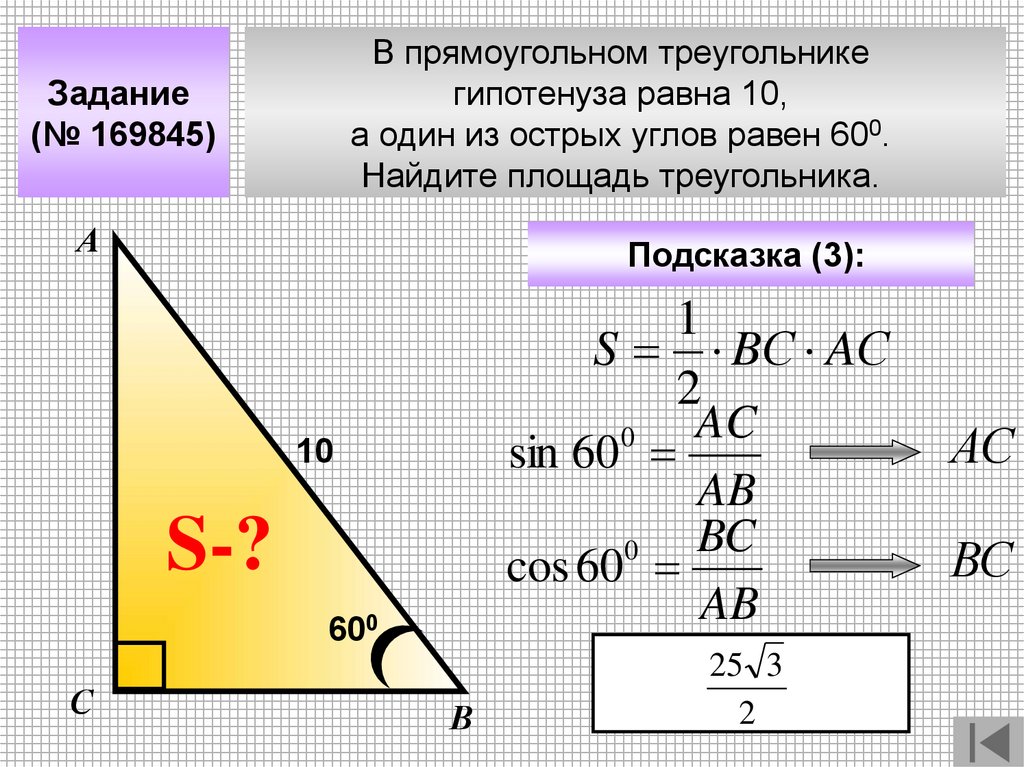
В прямоугольном треугольнике
гипотенуза равна 10,
а один из острых углов равен 600.
Найдите площадь треугольника.
Задание
(№ 169845)
А
Подсказка (3):
1
S BС AС
2
AC
0
sin 60
AB
BC
0
cos 60
AB
10
S-?
600
С
В
25 3
2
АС
ВС

11.

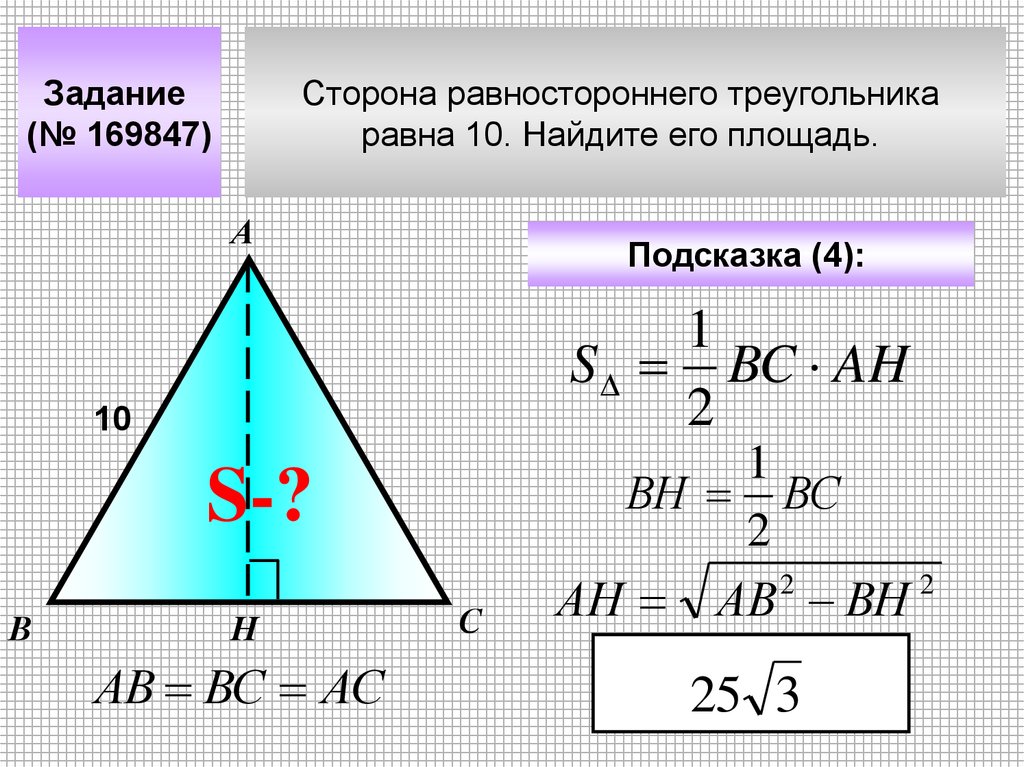
Задание
(№ 169847)
Сторона равностороннего треугольника
равна 10. Найдите его площадь.
А
Подсказка (4):
1
S BC AH
2
10
S-?
В
Н
АВ ВС АС
С
1
ВН ВС
2
2
2
АН АВ ВН
25 3

12.

Задание
(№ 169848)
Периметр равностороннего треугольника
равен 30. Найдите его площадь.
А
Подсказка (3):
1
S BC AH
2
АВ ВС АС
1
ВН ВС
2
S-?
25 3
В
Н
РАВС 30
С
АН АВ 2 ВН 2
25 3

13.

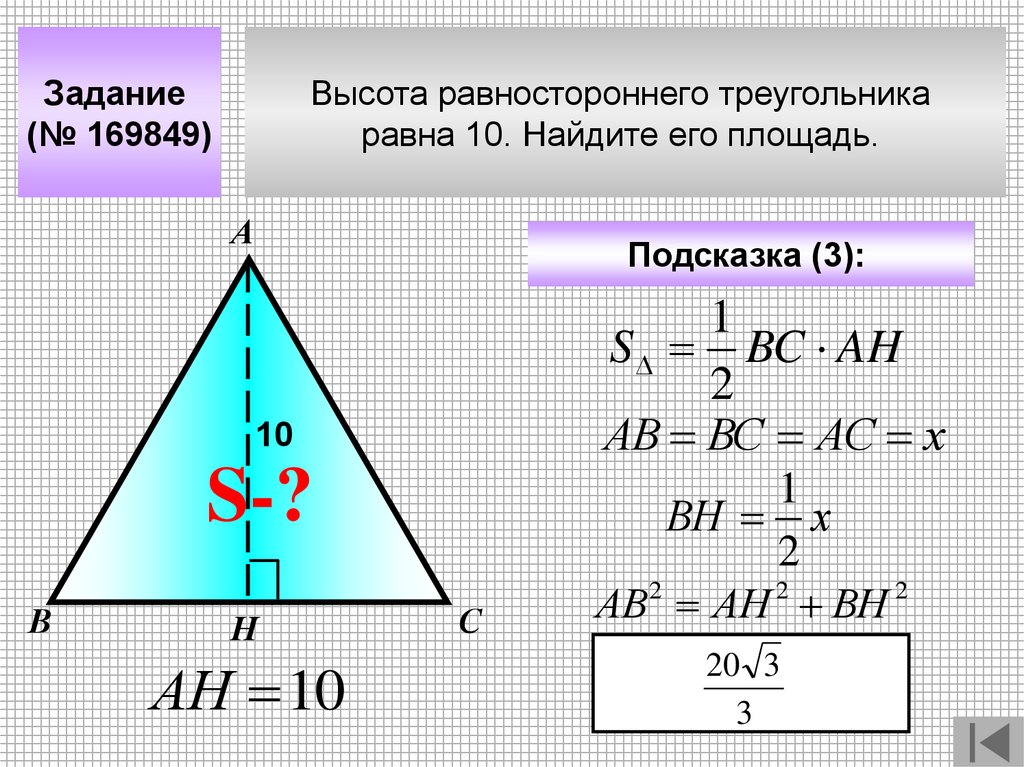
Задание
(№ 169849)
Высота равностороннего треугольника
равна 10. Найдите его площадь.
А
Подсказка (3):
1
S BC AH
2
АВ ВС АС х
10
S-?
1
ВН х
2
25 3
В
Н
АН 10
С
АВ2 АН 2 ВН 2
20 3
3

14.

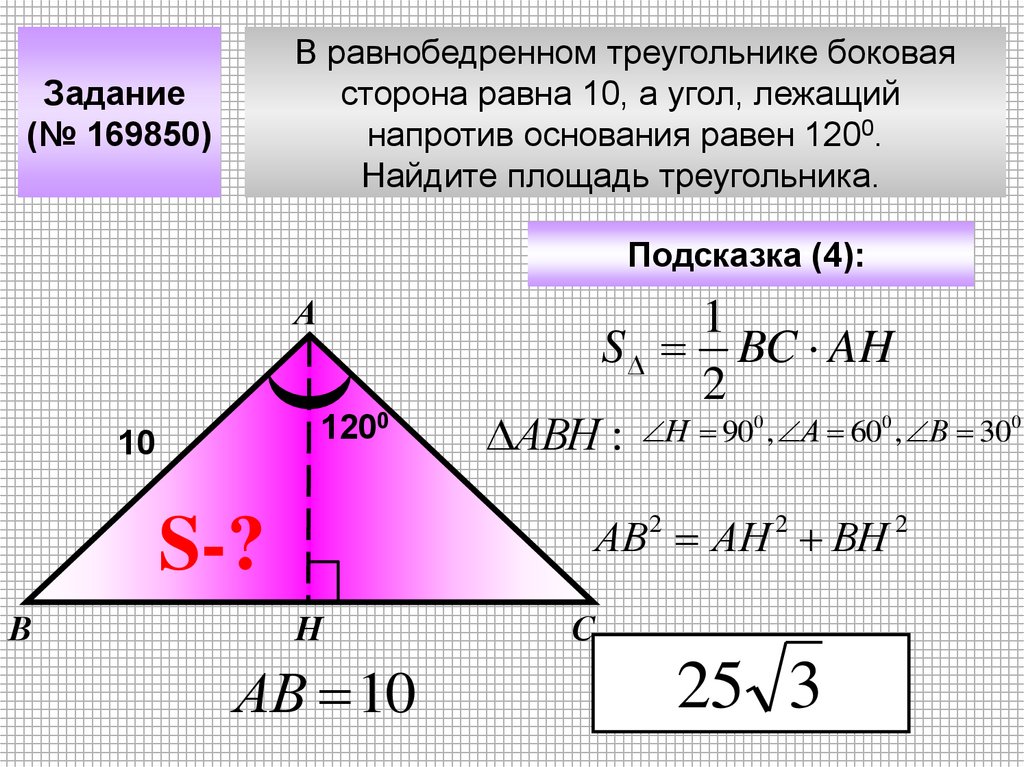
В равнобедренном треугольнике боковая
сторона равна 10, а угол, лежащий
напротив основания равен 1200.
Найдите площадь треугольника.
Задание
(№ 169850)
Подсказка (4):
А
1200
10
S-?
В
1
S BC AH
2
АВН : Н 90 , А 60 , В 30
0
0
АВ2 АН 2 ВН 2
25 3
Н
АВ 10
С
25 3
0

15.

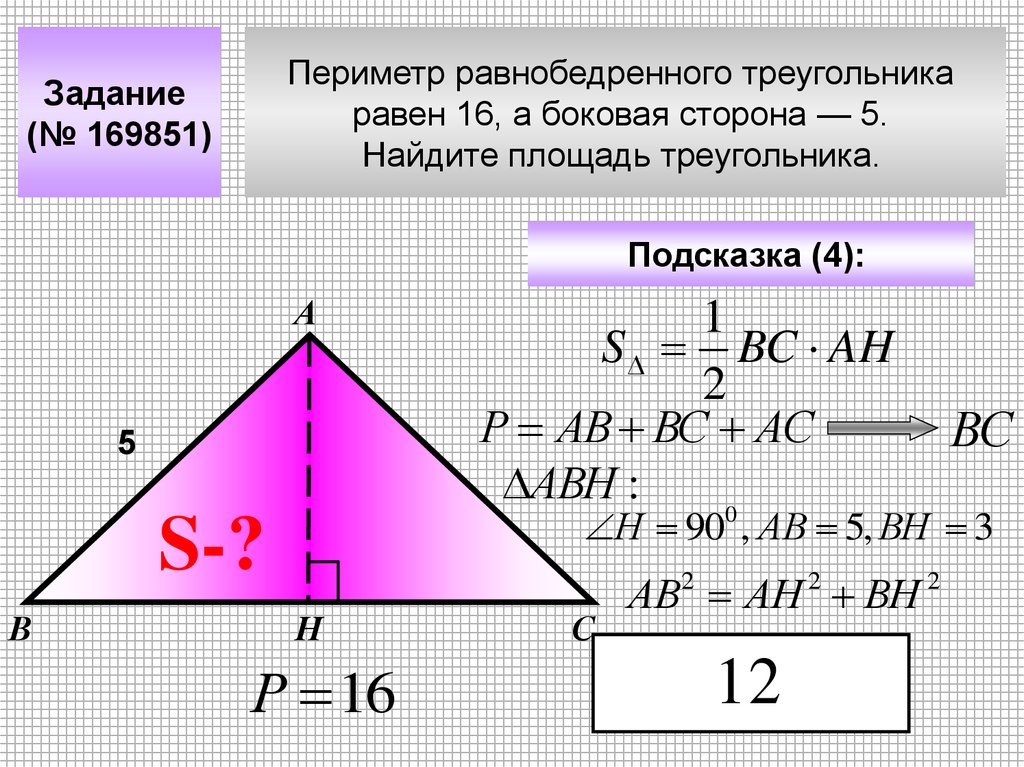
Периметр равнобедренного треугольника
равен 16, а боковая сторона — 5.
Найдите площадь треугольника.
Задание
(№ 169851)
Подсказка (4):
А
1
S BC AH
2
Р АВ ВС АС
АВН :
0
5
S-?
В
ВС
Н 90 , АВ 5, ВН 3
25 3
Н
Р 16
С
АВ2 АН 2 ВН 2
12

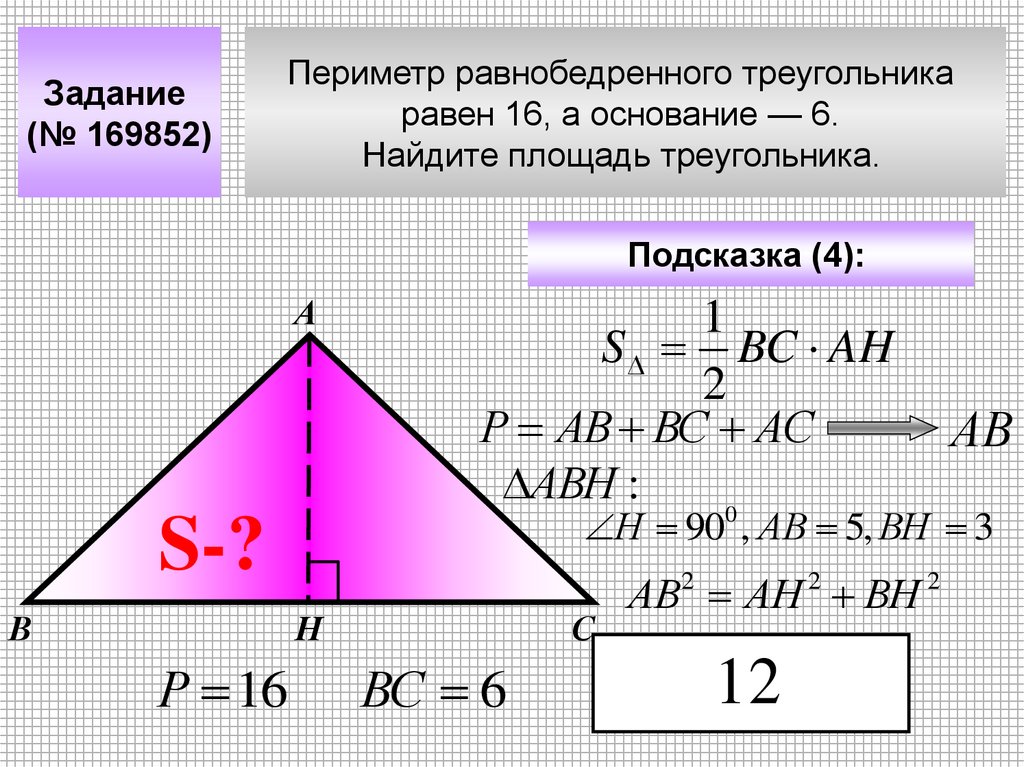
16.

Задание
(№ 169852)
Периметр равнобедренного треугольника
равен 16, а основание — 6.
Найдите площадь треугольника.
Подсказка (4):
А
S-?
В
1
S BC AH
2
Р АВ ВС АС
АВН :
0
Н 90 , АВ 5, ВН 3
25 3
Н
Р 16
АВ
С
ВС 6
АВ2 АН 2 ВН 2
12

17.

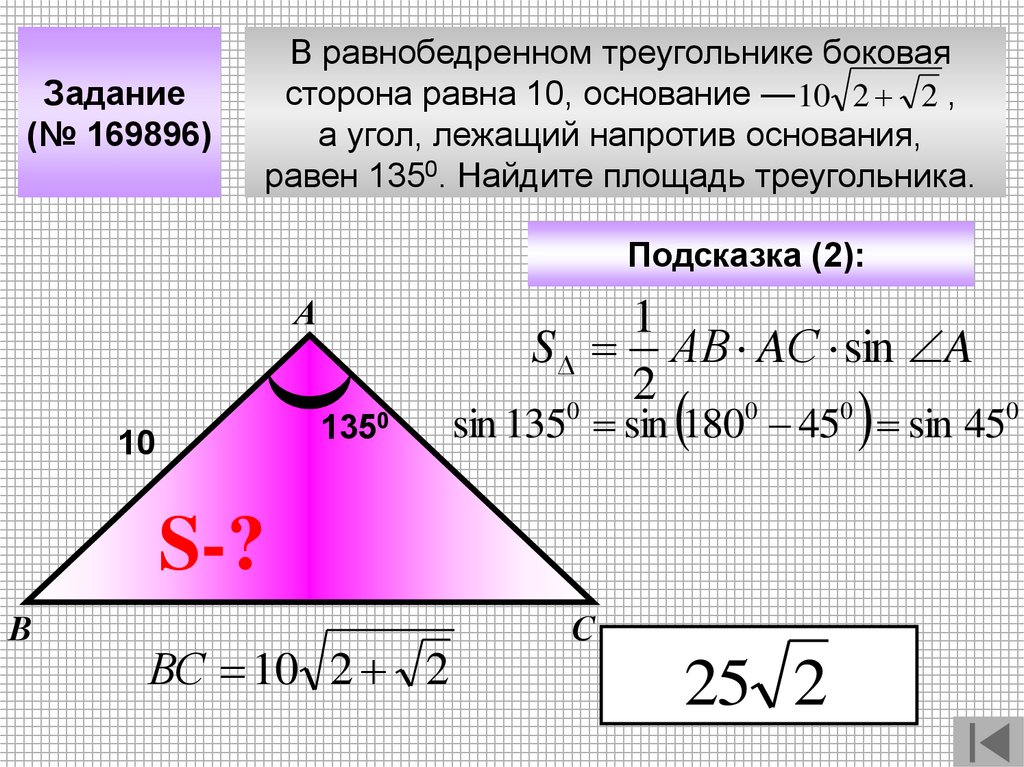
Задание
(№ 169896)
В равнобедренном треугольнике боковая
сторона равна 10, основание — 10 2 2 ,
а угол, лежащий напротив основания,
равен 1350. Найдите площадь треугольника.
Подсказка (2):
А
1350
10
1
S АB AС sin A
2
0
0
0
S-?
В
ВС 10 2 2
sin 135 sin 180 45 sin 450
С
25 2

18.

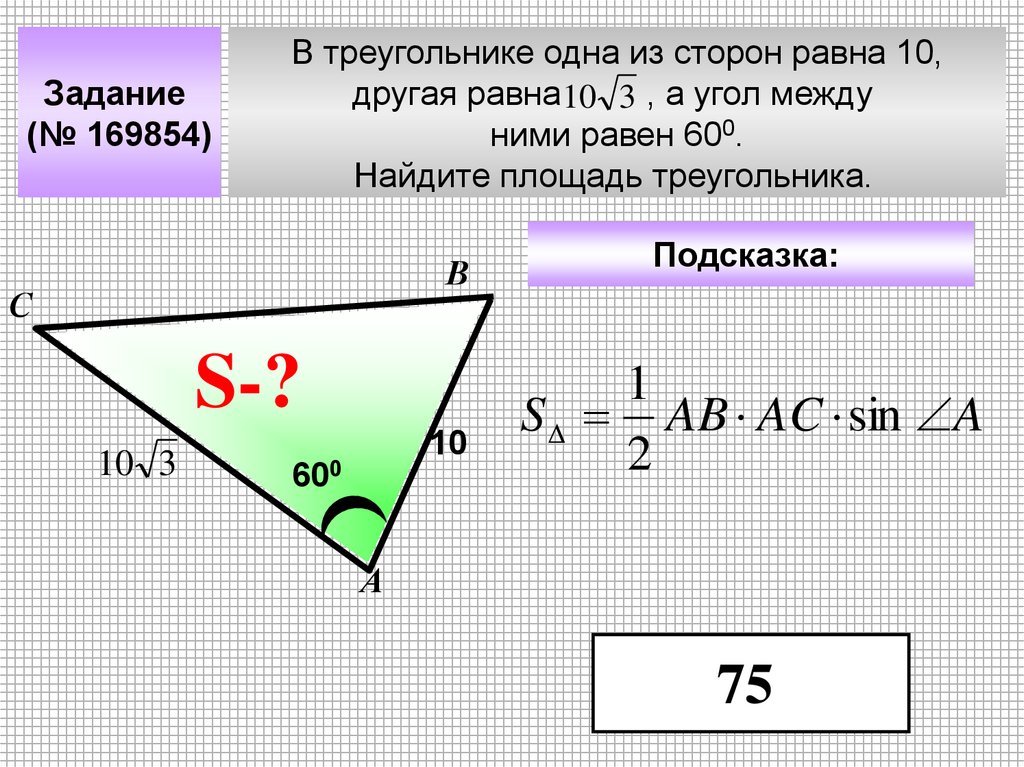
Задание
(№ 169854)
В треугольнике одна из сторон равна 10,
другая равна10 3 , а угол между
ними равен 600.
Найдите площадь треугольника.
В
С
S-?
10 3
10
?
600
Подсказка:
1
S AB AC sin A
2
А
75

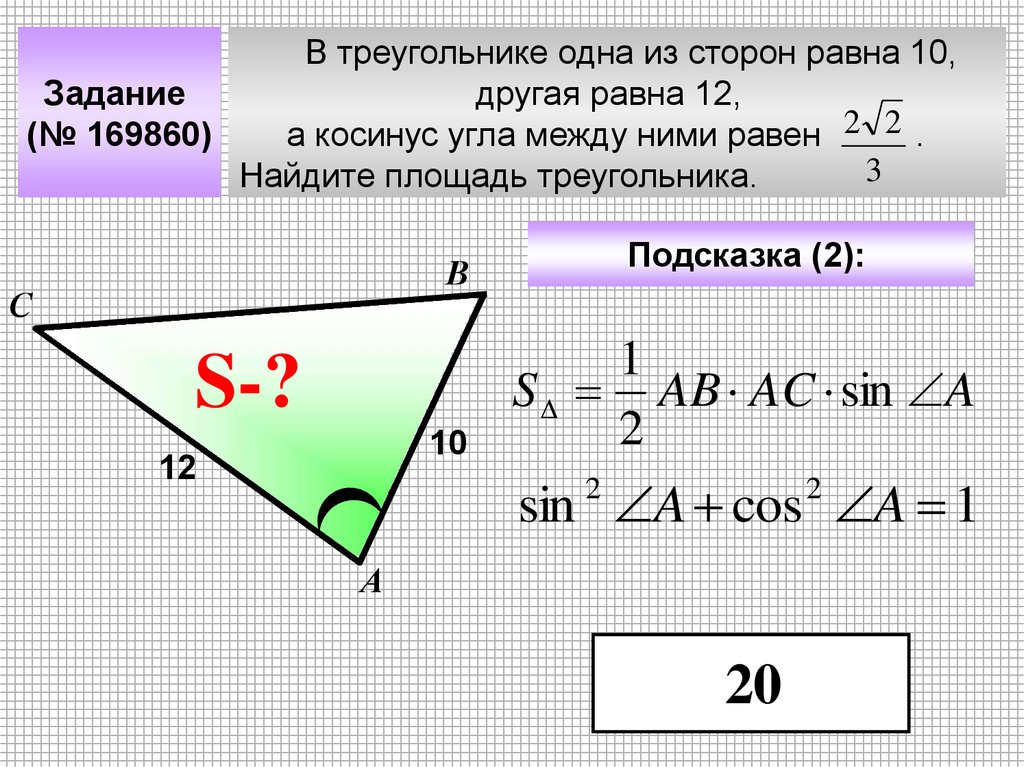
19.

В треугольнике одна из сторон равна 10,
Задание
другая равна 12,
(№ 169860)
а косинус угла между ними равен 2 2 .
3
Найдите площадь треугольника.
Подсказка (2):
В
С
S-?
12
10
?
1
S AB AC sin A
2
sin A cos A 1
2
2
А
20

20.

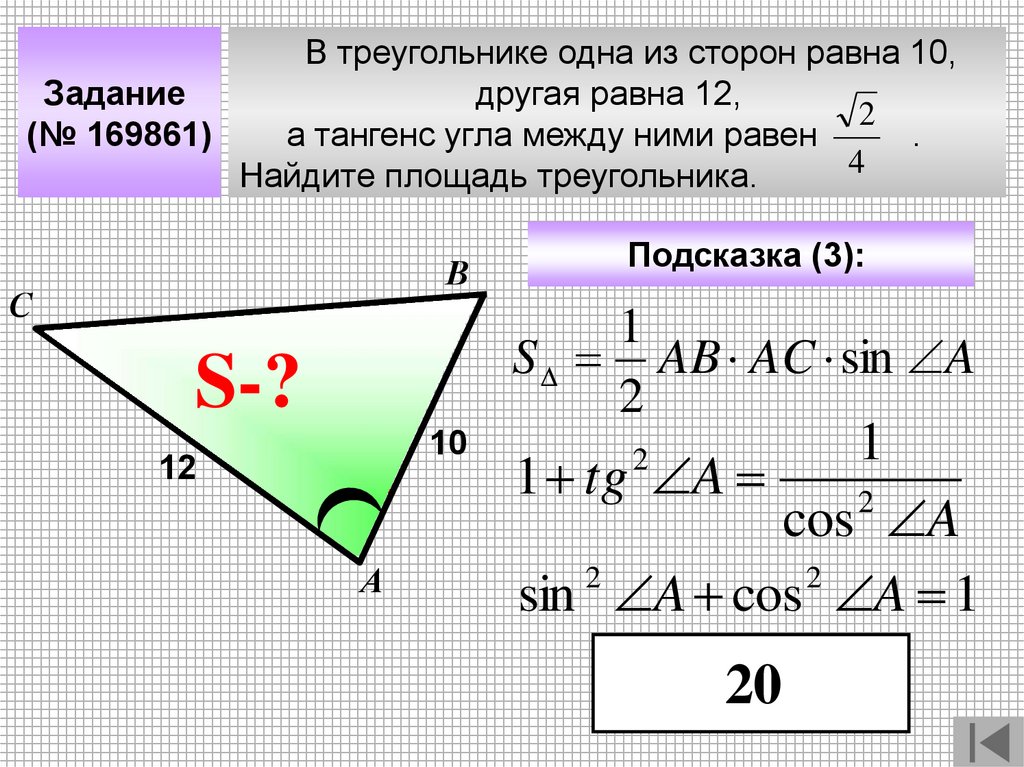
В треугольнике одна из сторон равна 10,
Задание
другая равна 12,
2
(№ 169861)
а тангенс угла между ними равен
.
4
Найдите площадь треугольника.
В
С
1
S AB AC sin A
2
S-?
12
Подсказка (3):
10
?
А
1 tg A
2
1
cos A
2
2
sin A cos A 1
20
2

21.

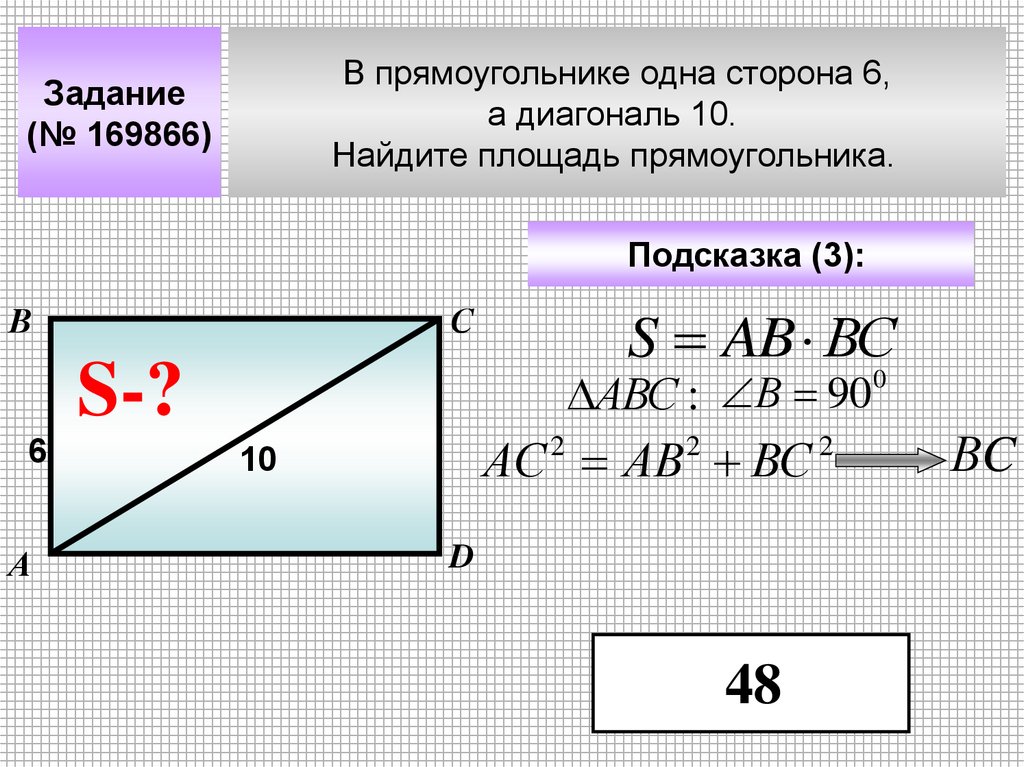
В прямоугольнике одна сторона 6,
а диагональ 10.
Найдите площадь прямоугольника.
Задание
(№ 169866)
Подсказка (3):
В
S-?
6
А
S AB ВC
С
0
В
90
АВС :
АС АВ ВС
2
10
2
D
48
2
ВC

22.

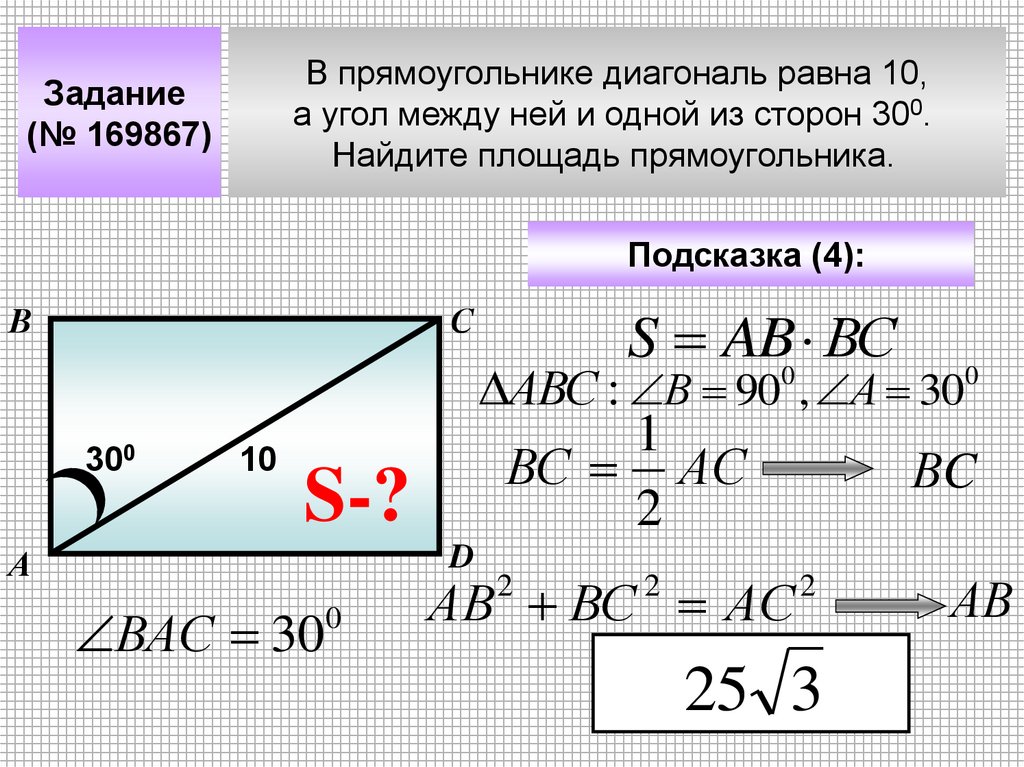
В прямоугольнике диагональ равна 10,
а угол между ней и одной из сторон 300.
Найдите площадь прямоугольника.
Задание
(№ 169867)
Подсказка (4):
В
S AB0 ВC
С
АВС : В 90 , А 30
300
10
1
ВС АС
2
S-?
D
А
ВАС 30
0
АВ ВС АС
2
2
0
ВC
2
25 3
АВ

23.

Задание
(№ 169898)
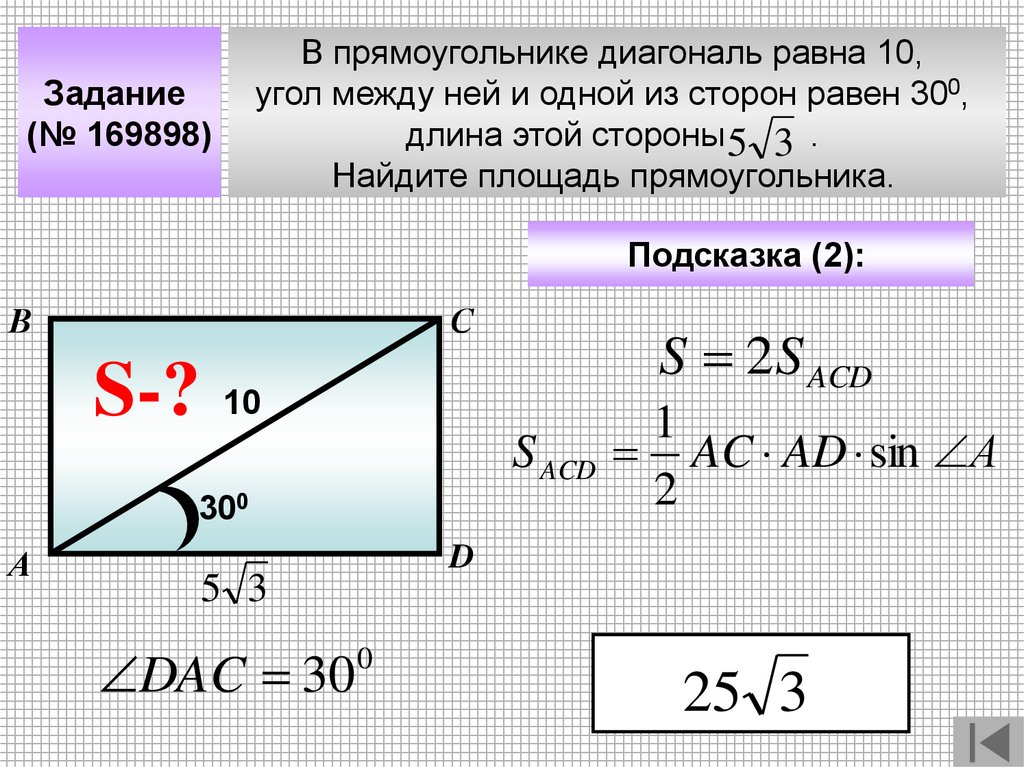
В прямоугольнике диагональ равна 10,
угол между ней и одной из сторон равен 300,
длина этой стороны 5 3 .
Найдите площадь прямоугольника.
Подсказка (2):
В
С
S 2S ACD
S-? 10
S ACD
300
А
D
5 3
DAC 30
1
AC AD sin А
2
0
25 3

24.

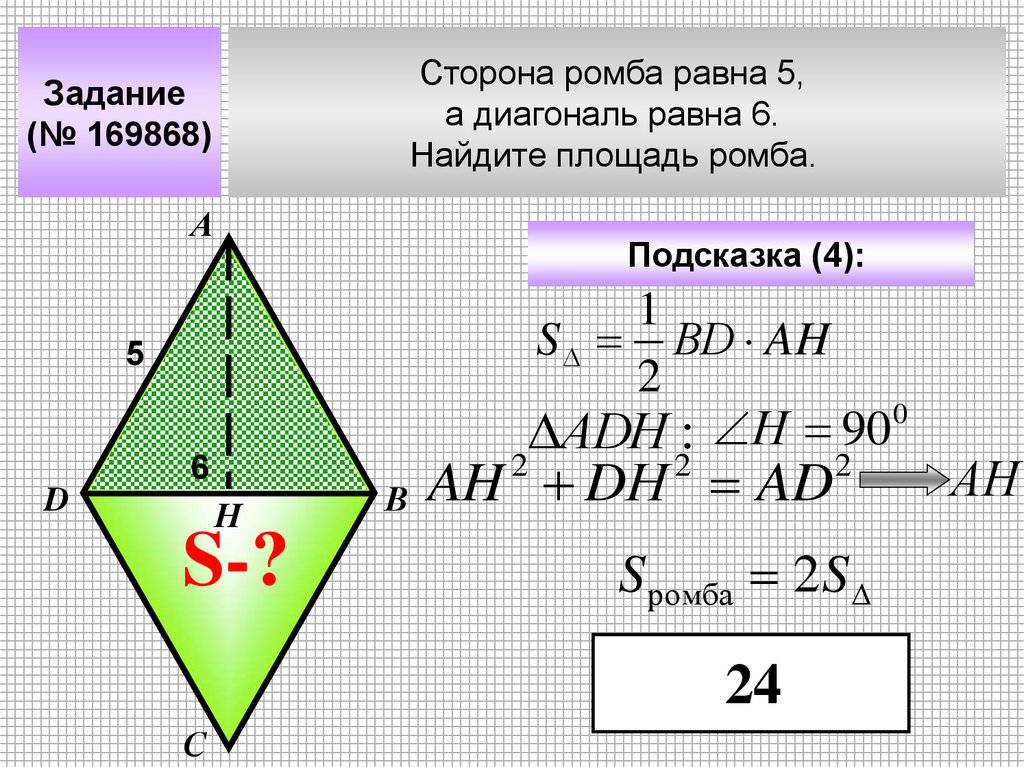
Сторона ромба равна 5,
а диагональ равна 6.
Найдите площадь ромба.
Задание
(№ 169868)
А
Подсказка (4):
1
S ВD AH
2
0
АDH : Н 90
5
6
D
Н
S-?
В
AH DН AD
2
2
S ромба 2 S
24
С
2
АН

25.

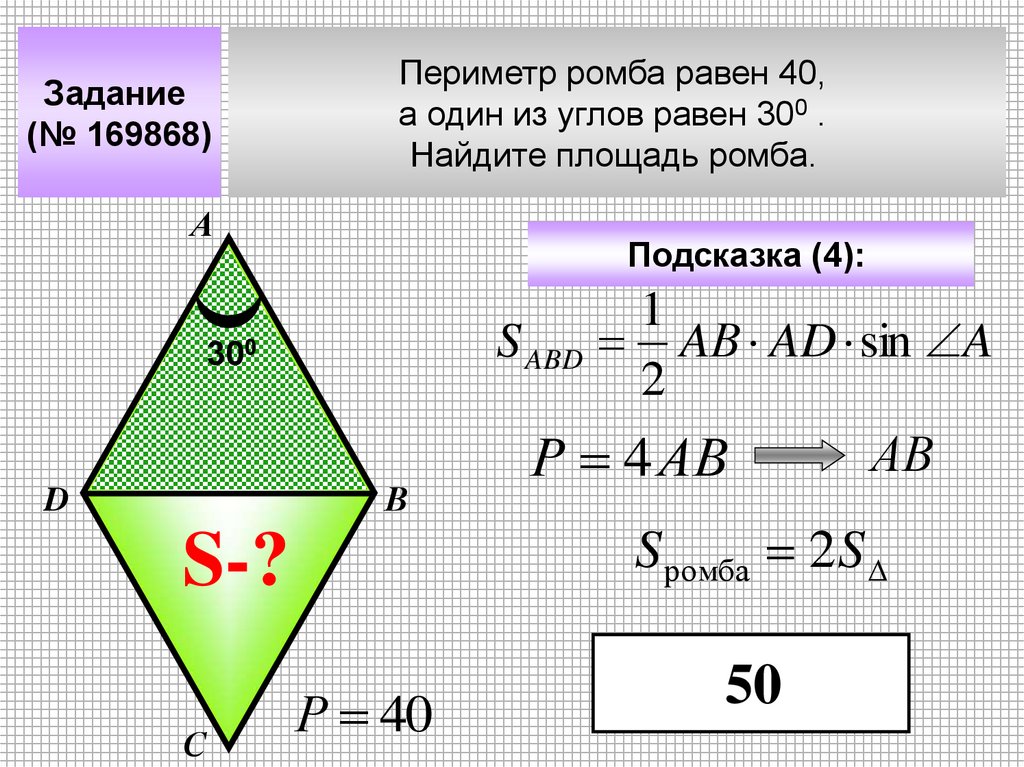
Задание
(№ 169868)
Периметр ромба равен 40,
а один из углов равен 300 .
Найдите площадь ромба.
А
Подсказка (4):
S ABD
300
В
D
S-?
С
Р 40
1
AВ AD sin A
2
Р 4 АВ
АВ
S ромба 2 S
50

26.

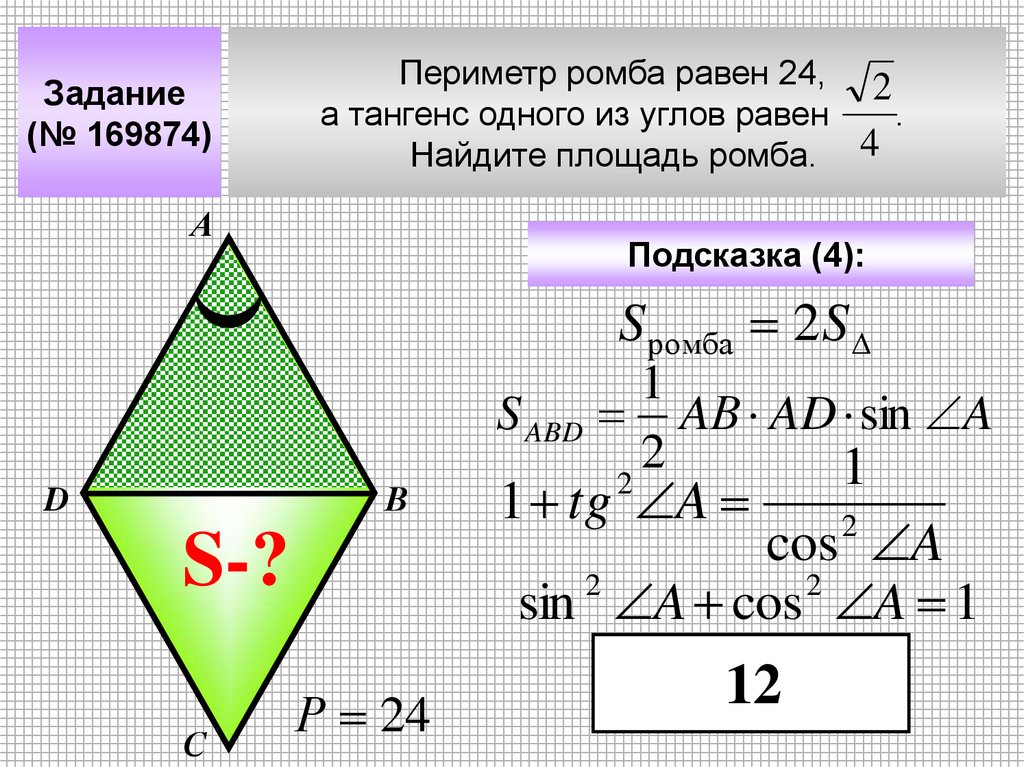
Задание
(№ 169874)
Периметр ромба равен 24, 2
а тангенс одного из углов равен
.
Найдите площадь ромба. 4
А
Подсказка (4):
S ромба 2 S
S ABD
В
D
S-?
С
Р 24
1
AВ AD sin A
2
1
1 tg A
2
cos A
2
2
sin A cos A 1
12
2

27.

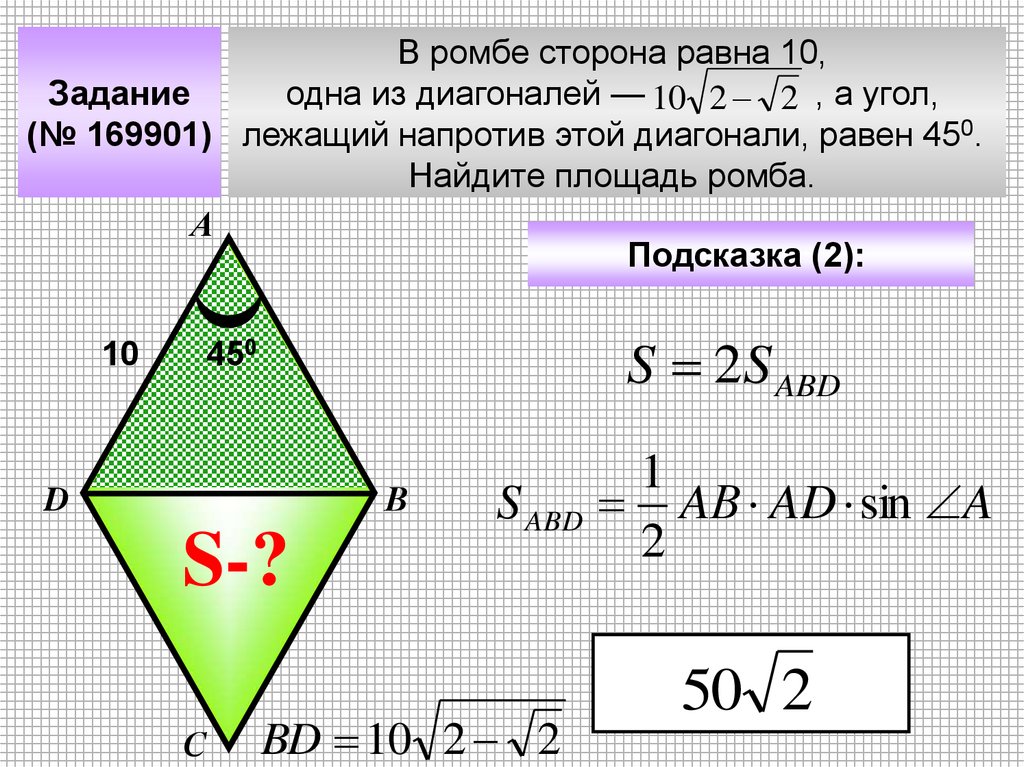
В ромбе сторона равна 10,
Задание
одна из диагоналей — 10 2 2 , а угол,
(№ 169901) лежащий напротив этой диагонали, равен 450.
Найдите площадь ромба.
А
Подсказка (2):
S 2S ABD
450
10
В
D
S-?
С
S ABD
BD 10 2 2
1
AВ AD sin A
2
50 2

28.

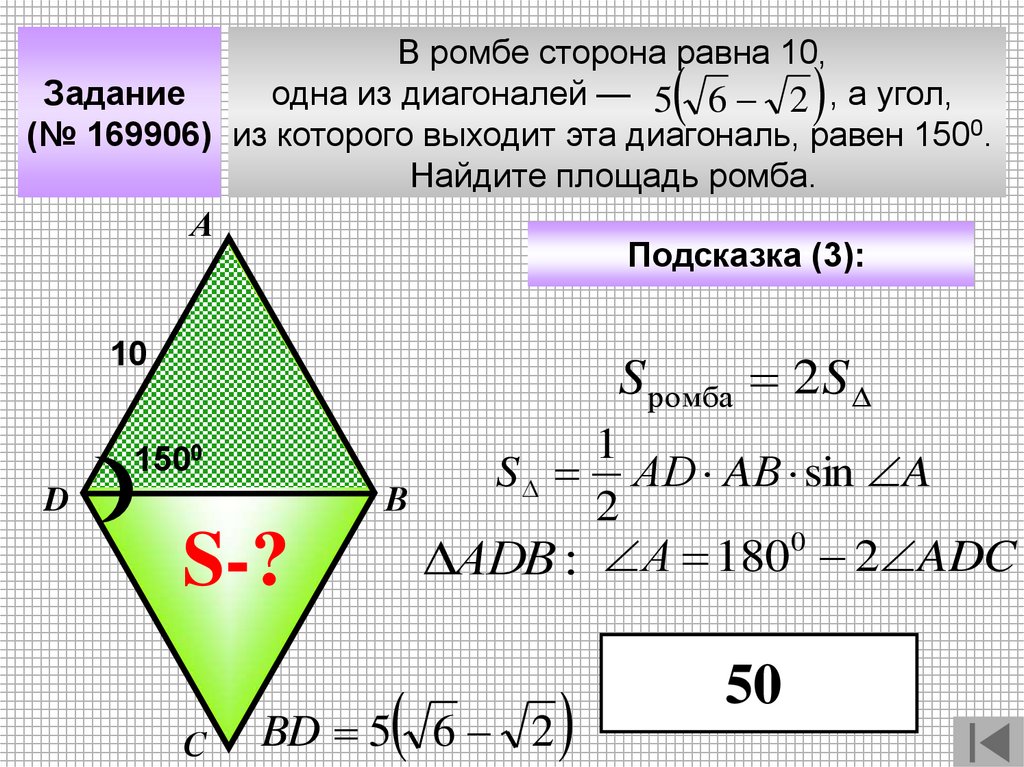
В ромбе сторона равна 10,
Задание
одна из диагоналей — 5 6 2 , а угол,
(№ 169906) из которого выходит эта диагональ, равен 1500.
Найдите площадь ромба.
А
Подсказка (3):
10
S ромба 2 S
1500
В
D
S-?
С
1
S АD AВ sin A
2
0
АDВ : А 180 2 ADC
BD 5 6 2
50

29.

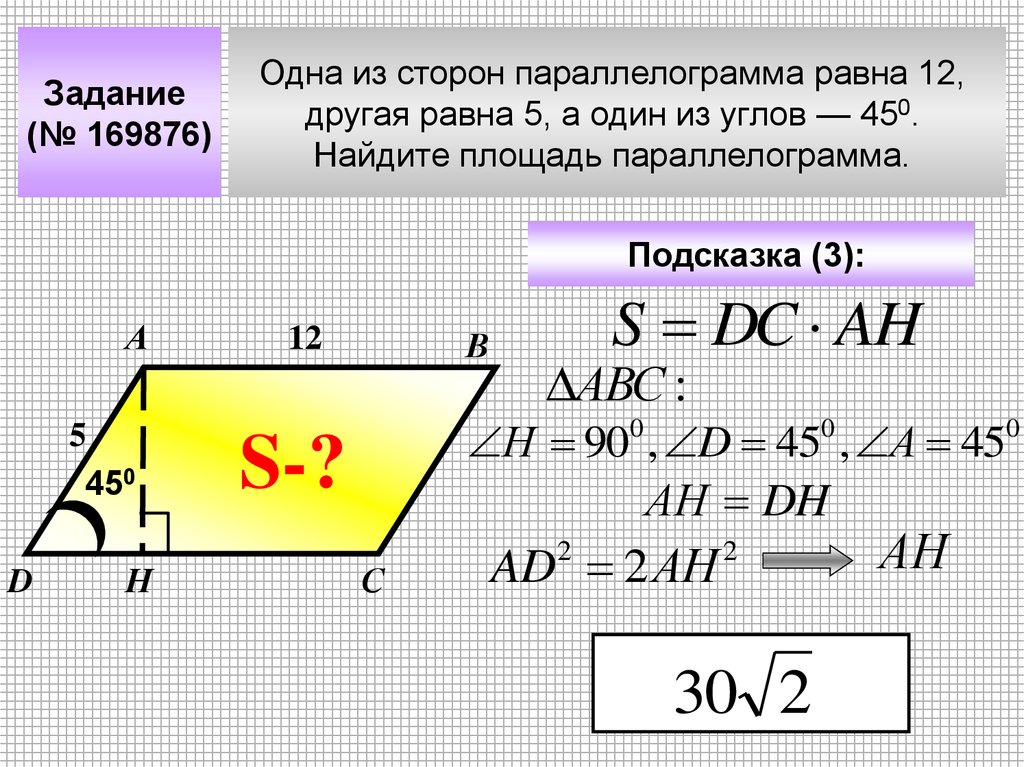
Задание
(№ 169876)
Одна из сторон параллелограмма равна 12,
другая равна 5, а один из углов — 450.
Найдите площадь параллелограмма.
Подсказка (3):
А
5
450
D
Н
12
В
S DC AH
АВС :
Н 90 , D 45 , А 45
АН DH
0
S-?
С
0
AD 2АН
2
2
30 2
0
АН

30.

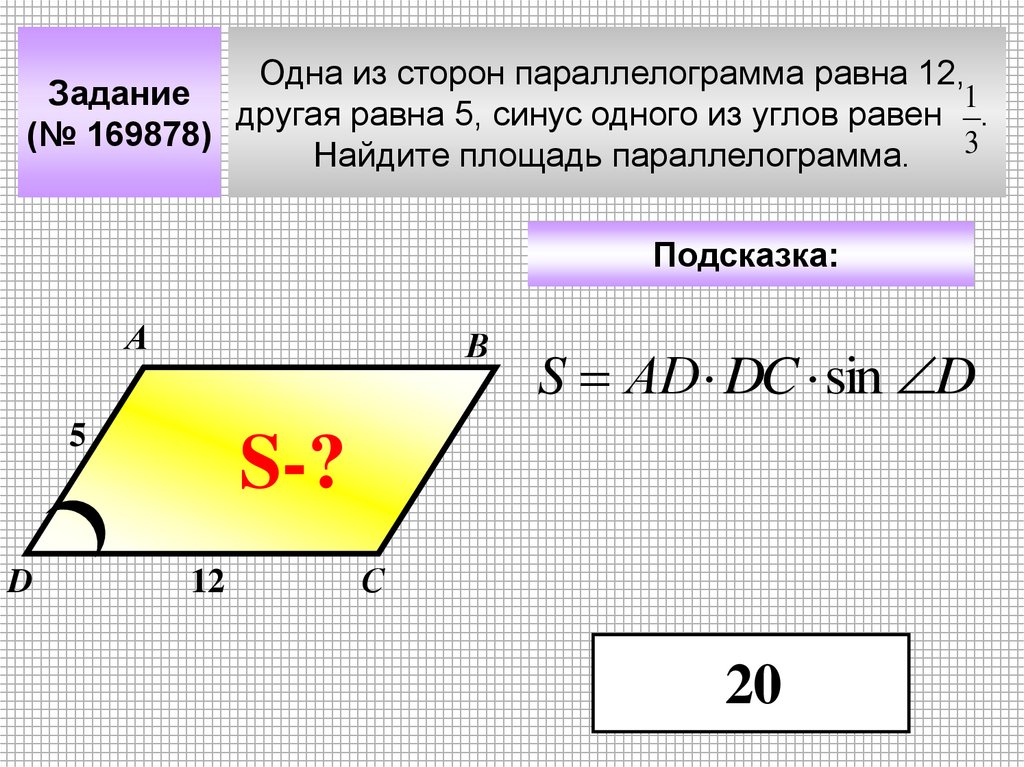
Одна из сторон параллелограмма равна 12,
Задание
1
другая равна 5, синус одного из углов равен .
(№ 169878)
3
Найдите площадь параллелограмма.
Подсказка:
А
В
5
D
S АD DC sin D
S-?
12
С
20

31.

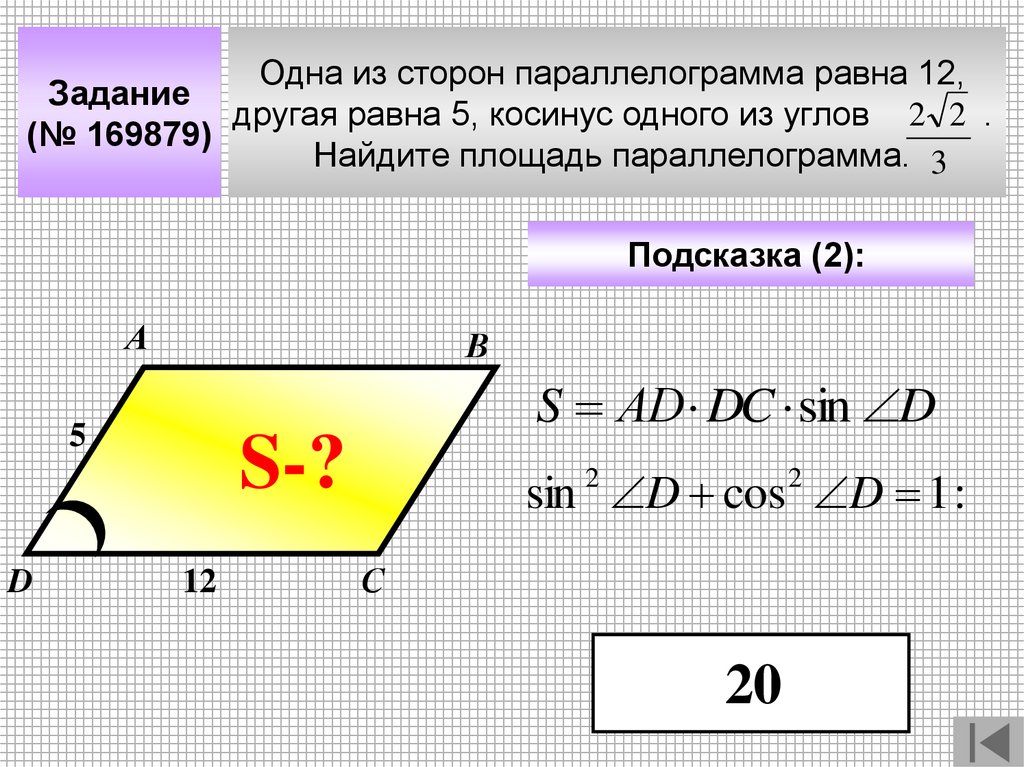
Одна из сторон параллелограмма равна 12,
Задание
другая равна 5, косинус одного из углов 2 2 .
(№ 169879)
Найдите площадь параллелограмма. 3
Подсказка (2):
А
В
S АD DC sin D
5
D
S-?
12
sin D cos D 1 :
2
2
С
20

32.

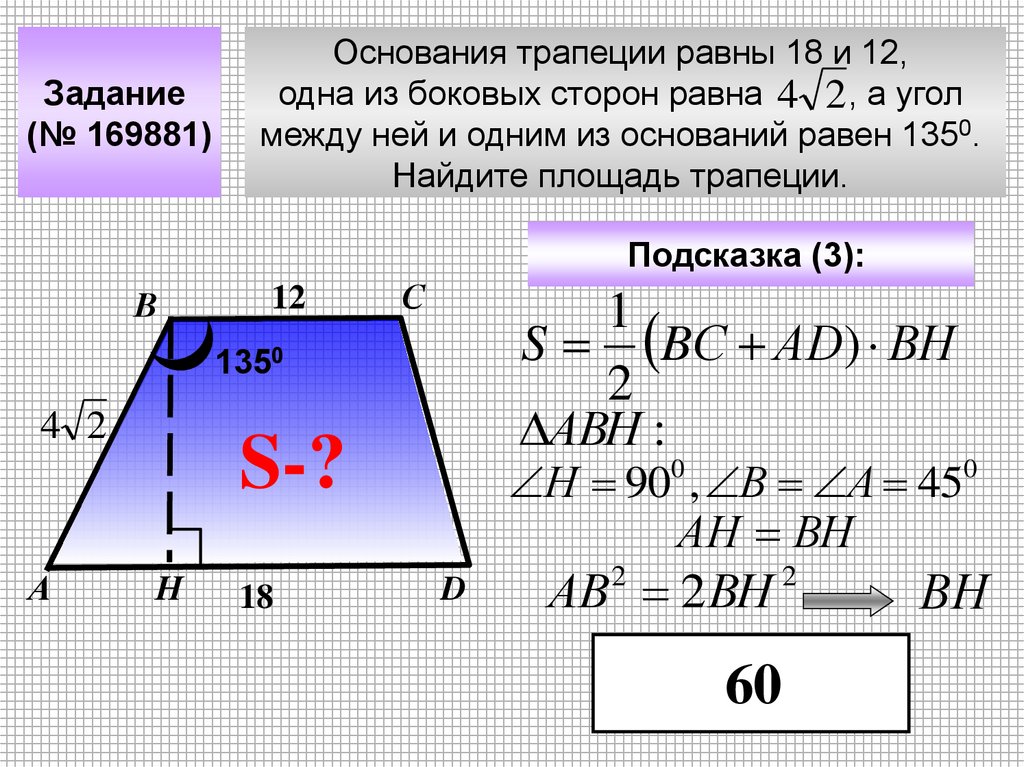
Задание
(№ 169881)
Основания трапеции равны 18 и 12,
одна из боковых сторон равна 4 2 , а угол
между ней и одним из оснований равен 1350.
Найдите площадь трапеции.
Подсказка (3):
В
12
С
1
S BС АD) ВН
2
АВН :
1350
4 2
А
S-?
Н
18
Н 90 , В А 45
АН ВН
0
D
0
АВ 2ВН
2
60
2
ВН

33.

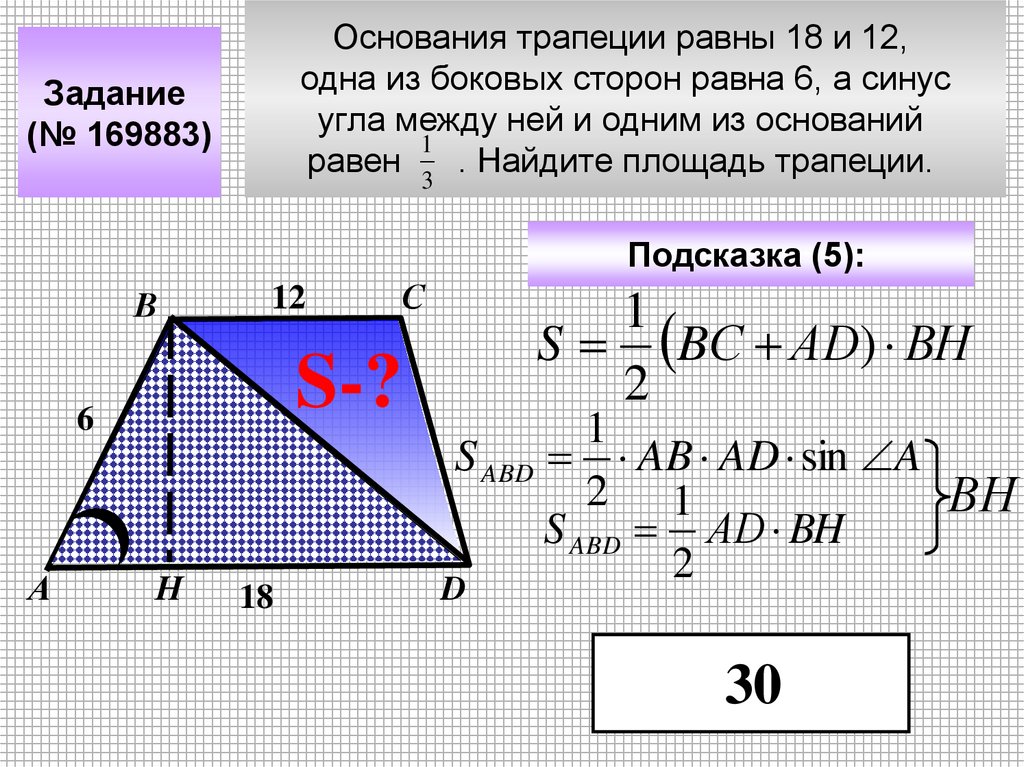
Основания трапеции равны 18 и 12,
одна из боковых сторон равна 6, а синус
угла между ней и одним из оснований
1
равен 3 . Найдите площадь трапеции.
Задание
(№ 169883)
Подсказка (5):
В
12
S-?
6
А
С
Н
18
1
S BС АD) ВН
2
1
S ABD AB AD sin A
2 1
ВН
S ABD АD BH
2
D
30

34.

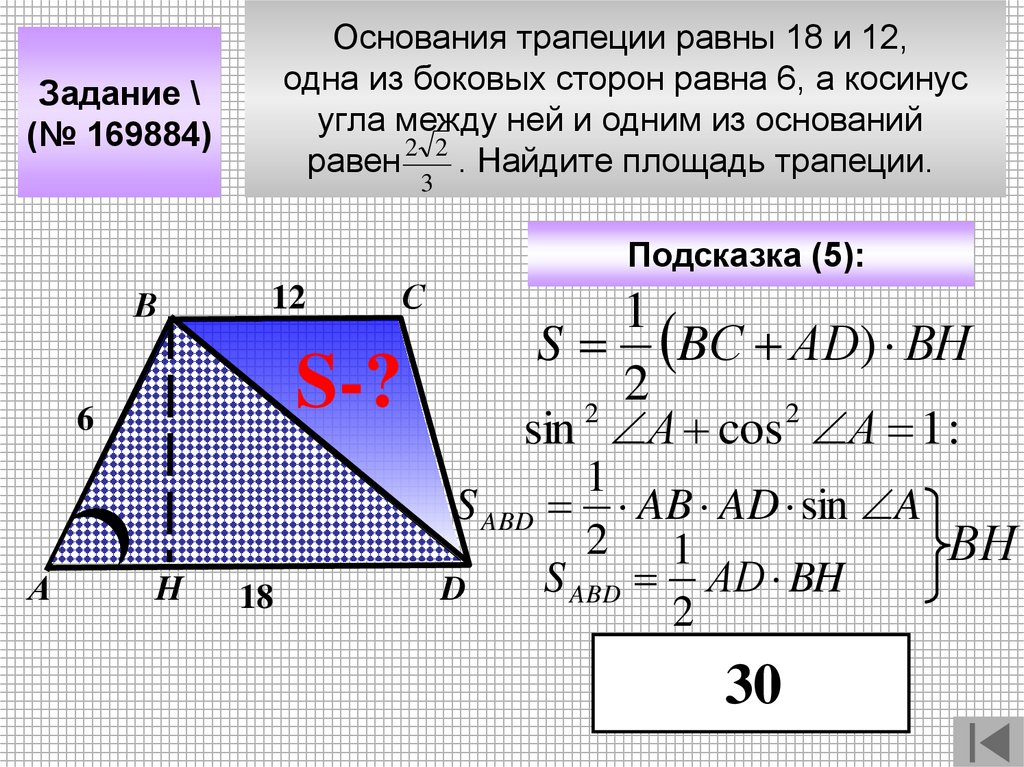
Основания трапеции равны 18 и 12,
одна из боковых сторон равна 6, а косинус
угла между ней и одним из оснований
равен 2 2 . Найдите площадь трапеции.
Задание \
(№ 169884)
3
Подсказка (5):
В
12
S-?
6
А
С
Н
18
1
S BС АD) ВН
2
2
2
sin А cos А 1 :
1
S ABD AB AD sin A
2 1
ВН
S ABD АD BH
D
2
30

35.

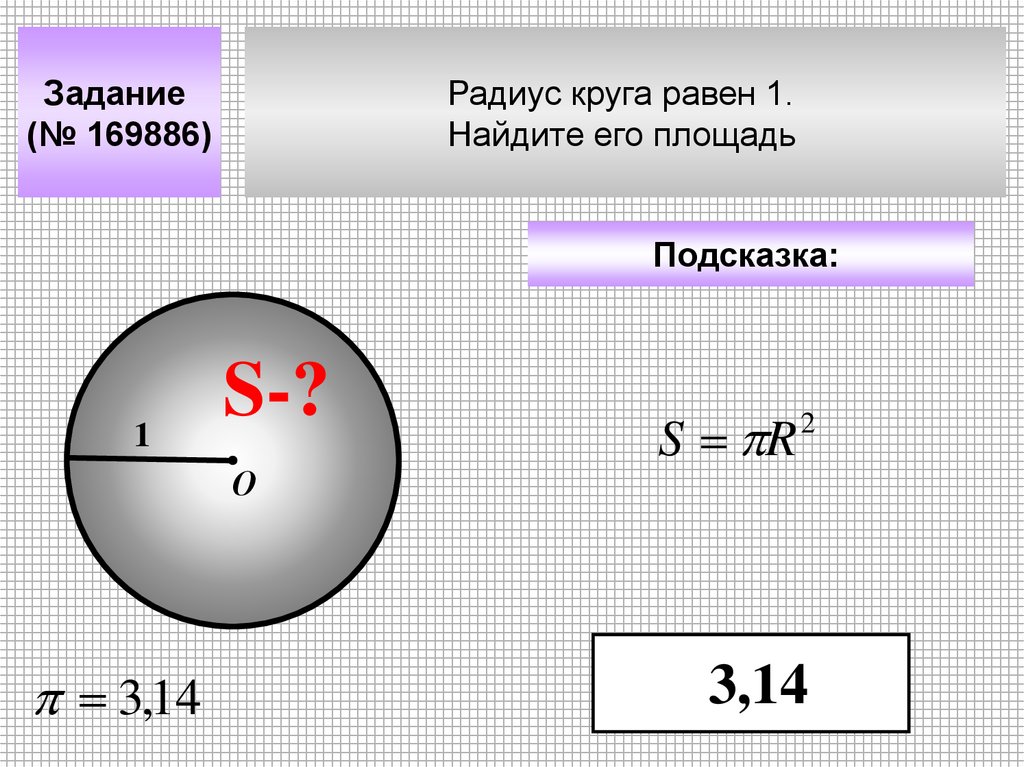
Задание
(№ 169886)
Радиус круга равен 1.
Найдите его площадь
Подсказка:
1
S-?
О
3,14
S R
2
3,14

36.

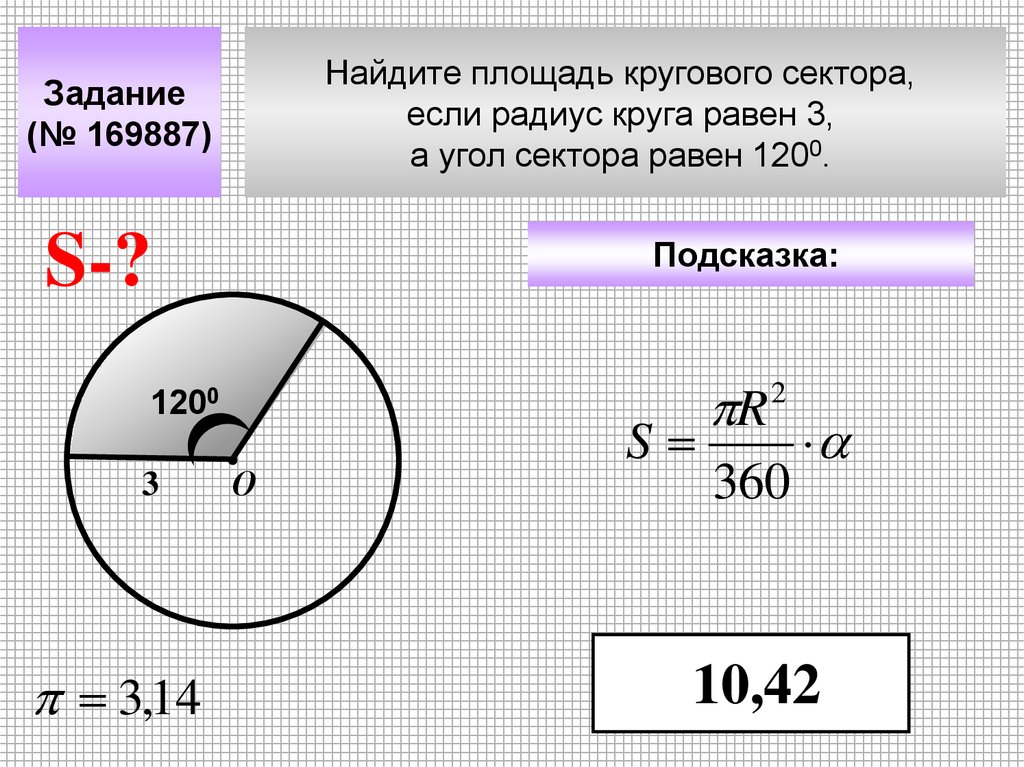
Найдите площадь кругового сектора,
если радиус круга равен 3,
а угол сектора равен 1200.
Задание
(№ 169887)
S-?
Подсказка:
1200
3
3,14
О
S
R
2
360
10,42

37.

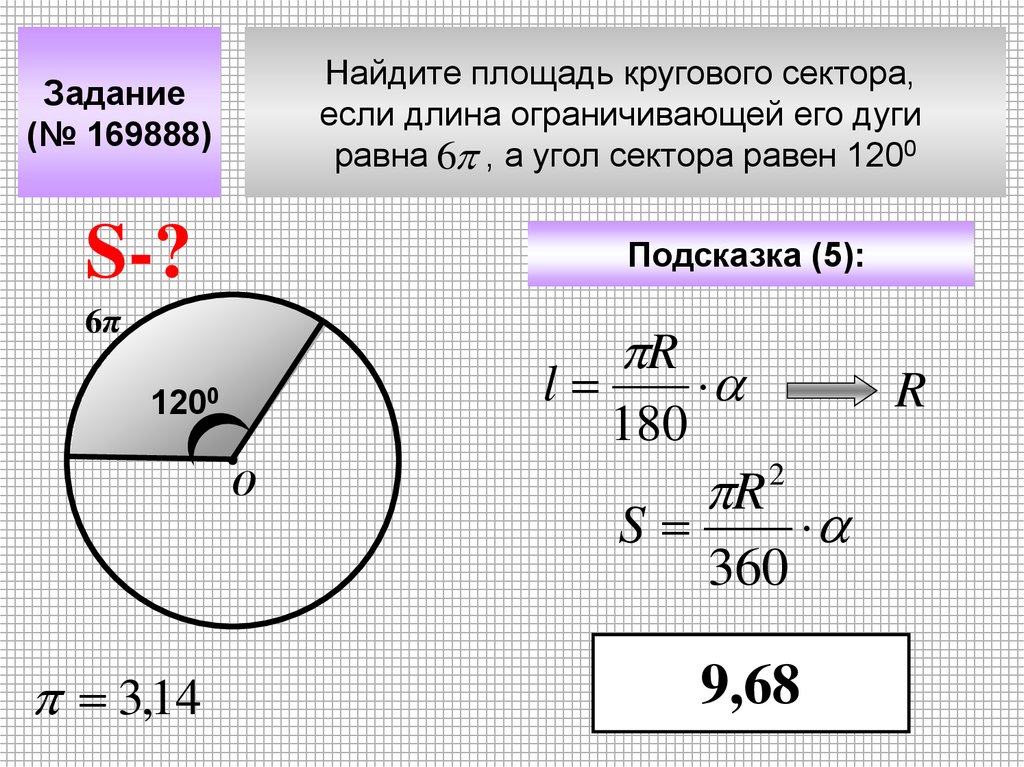
Найдите площадь кругового сектора,
если длина ограничивающей его дуги
равна 6 , а угол сектора равен 1200
Задание
(№ 169888)
S-?
Подсказка (5):
6π
R
l
1200
О
3,14
180
S
R
R
2
360
9,68

38.

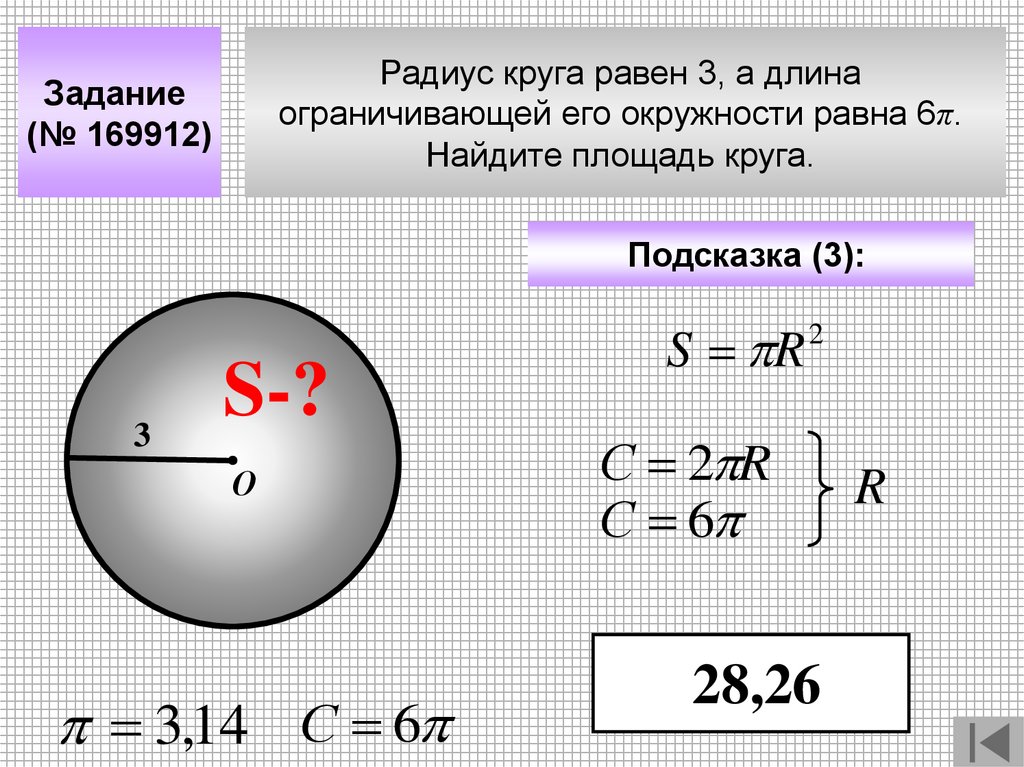
Радиус круга равен 3, а длина
ограничивающей его окружности равна 6π.
Найдите площадь круга.
Задание
(№ 169912)
Подсказка (3):
3
S-?
О
3,14 С 6
S R
2
С 2 R
С 6
28,26
R

39.

При создании презентации были использованы
задачи с сайта
«Открытый банк заданий по математике»
.
http://www.mathgia.ru:8080/or/gia12/Main.html?view=Pos
Спасибо за проявленный интерес
к данной разработке!
ВСЕМ ТВОРЧЕСКИХ УСПЕХОВ
И УСПЕШНЫХ УЧЕНИКОВ!