Теорема о площади треугольника, теоремы синусов и косинусов

1.

2.

Повторение
№ 1013 (б)
2
Дано: cos
3
Найти: sin α
Решение:
sin²α + cos²α = 1
2
2
sin 2 1
3
4
1
9
4 5
sin 2 1
9 9
sin 2
sin
5
5
9
3
5
Ответ: sin
3
№ 1014 (а)
№ 1015 (а)
3
Дано: cos α = 1
Найти: sin α, tg α
Решение:
Дано: sin
2
Найти: cos α
Решение:
sin²α + cos²α = 1
2
3
cos 2 1
2
3
cos 2 1
4
3 1
cos 1
4 4
2
cos
sin²α + 1² = 1, sin²α = 0
sin α = 0
tg
sin
cos
tg α = 0 ÷ 1 = 0
1
1
4
2
Ответ: cos
sin²α + cos²α = 1
1
2
Ответ: sin α = 0, tg α = 0.

3.

№ 1016
sin 120º = sin (180º - 60º) = sin 60º 3
2
cos 120º = cos (180º - 60º)= – cos 60º
tg
sin
cos
tg
3 1
3 2
2 2
2 1
1
2
3
Вычислить самостоятельно: sin 135º, cos 135º, tg 135º
sin 135º = sin (180º - 45º) = sin 45º
2
2
cos 135º = cos (180º - 45º) = – cos 45º
tg
sin
cos
2
2
tg
2 2
1
2
2

4.

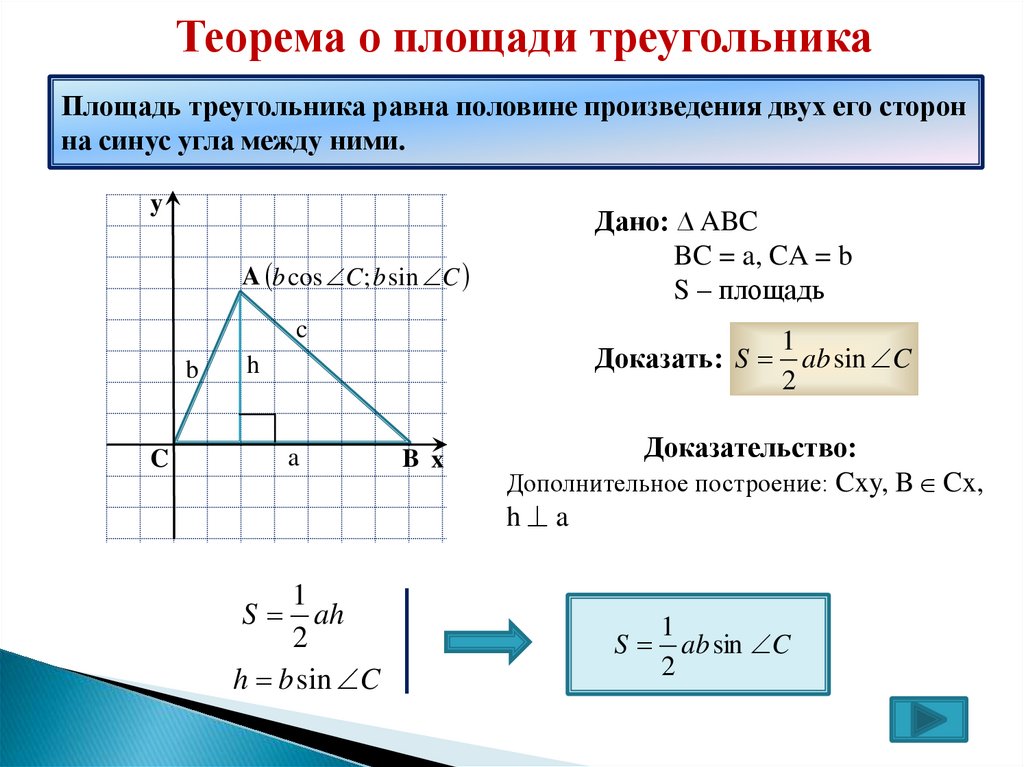
Теорема о площади треугольника
Площадь треугольника равна половине произведения двух его сторон
на синус угла между ними.
y
A b cos C ; b sin C
c
b
Доказать: S
h
a
C
1
ah
2
h b sin C
S
Дано: ∆ ABC
BC = a, CA = b
S – площадь
B x
1
ab sin C
2
Доказательство:
Дополнительное построение: Cxy, B Cx,
h a
S
1
ab sin C
2

5.

№ 1020 (а)
B
A
Дано: ∆ ABC
AB = 6 8 см, AC = 4 см
C
A 600
Найти: S
Решение:
1
AB AC sin A
2
1
1
3
S 6 8 4 sin 600 6 8 4
6 4 2 3 12 6 см²
2
2
2
S
Ответ: S 12 6 см².

6.

№ 1022
B
Дано: ∆ ABC
S = 60 см², AC = 15 см
A 300
A
C
Найти: AB
Решение:
1
S AB AC sin A
2
1
60 AB 15 sin 300
2
1
1
60 AB 15
2
2
Ответ: AB = 16 см.
4
AB 60
15 60 4
16 см
4
1 15 1