Решение треугольников

1.

2. В науке нет широкой столбовой дороги и только тот достигнет ее сияющих вершин, кто не страшась усталости карабкается по ее

каменистым тропам.
К. Маркс

3.

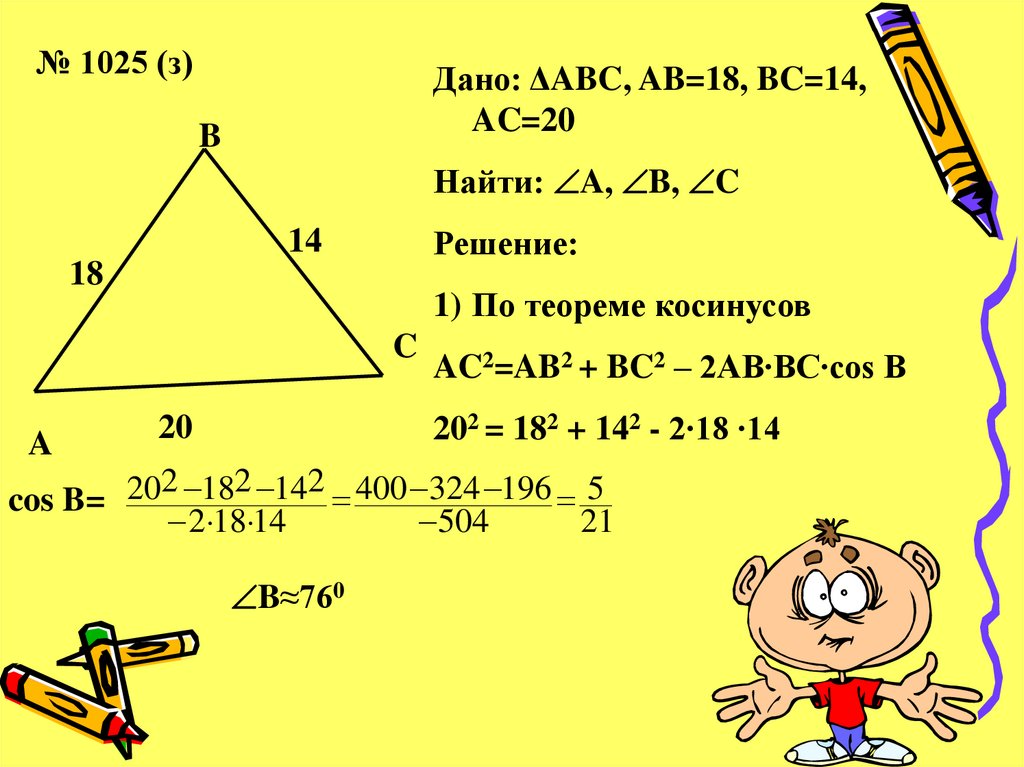
№ 1025 (з)
Дано: ΔABC, AB=18, BC=14,
AC=20
B
Найти: A, B, C
Решение:
14
18
1) По теореме косинусов
C
A
AC2=AB2 + BC2 – 2AB∙BC∙cos B
202 = 182 + 142 - 2∙18 ∙14
20
2
2
2
cos B= 20 18 14 400 324 196 5
2 18 14
504
21
B≈760

4.

2)по теореме синусов
AC BC
sin B sin A
0
BC
sin
B
14
sin
76
sin A
0,6792
AC
20
A≈430
C=1800 – 760 – 430 =610

5.

Дано
Найти
Решение
B
a
C
a, B, C
A, b, c
A=1800– ( B + C)
a b c
sin A sin B sin C
b a sin B ;c a sin C
sin A
sin A

6.

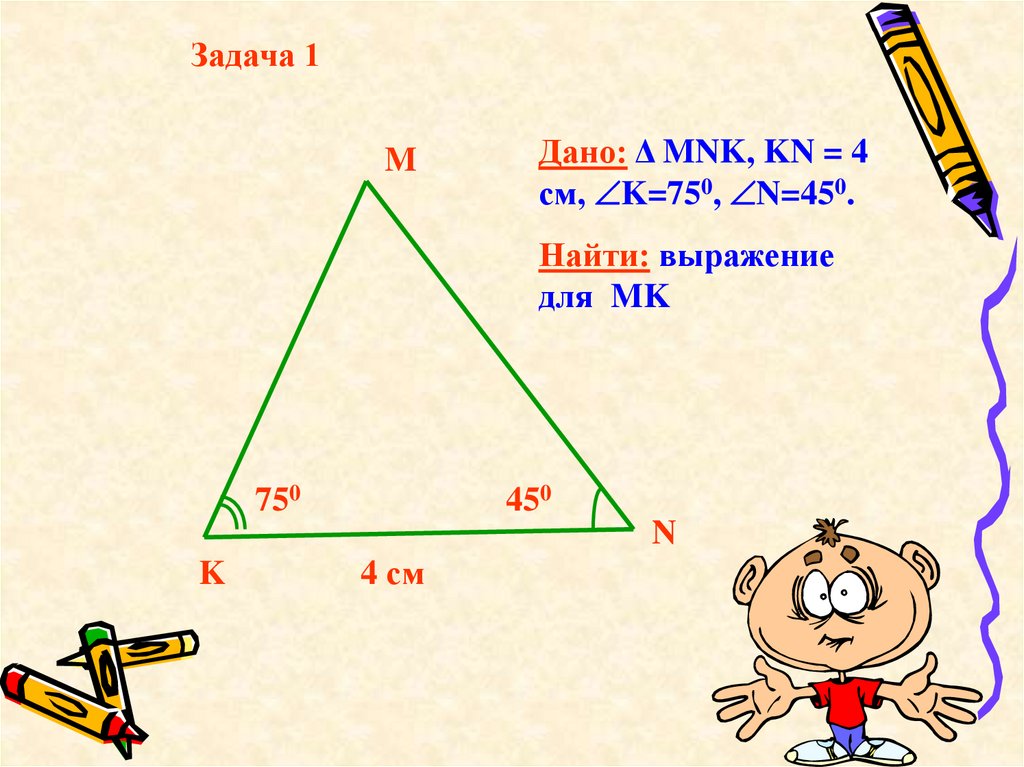
Задача 1
M
Дано: Δ MNK, KN = 4
см, K=750, N=450.
Найти: выражение
для MK
750
450
N
K
4 см

7.

Ответ: 1) М=1800–1200=600
2) по теореме синусов
MK
KN
sin N sin M
MK
4
0
0
sin 45
sin 60
2
4
2 2 2 12 2
2
MK
3
3
3
2

8.

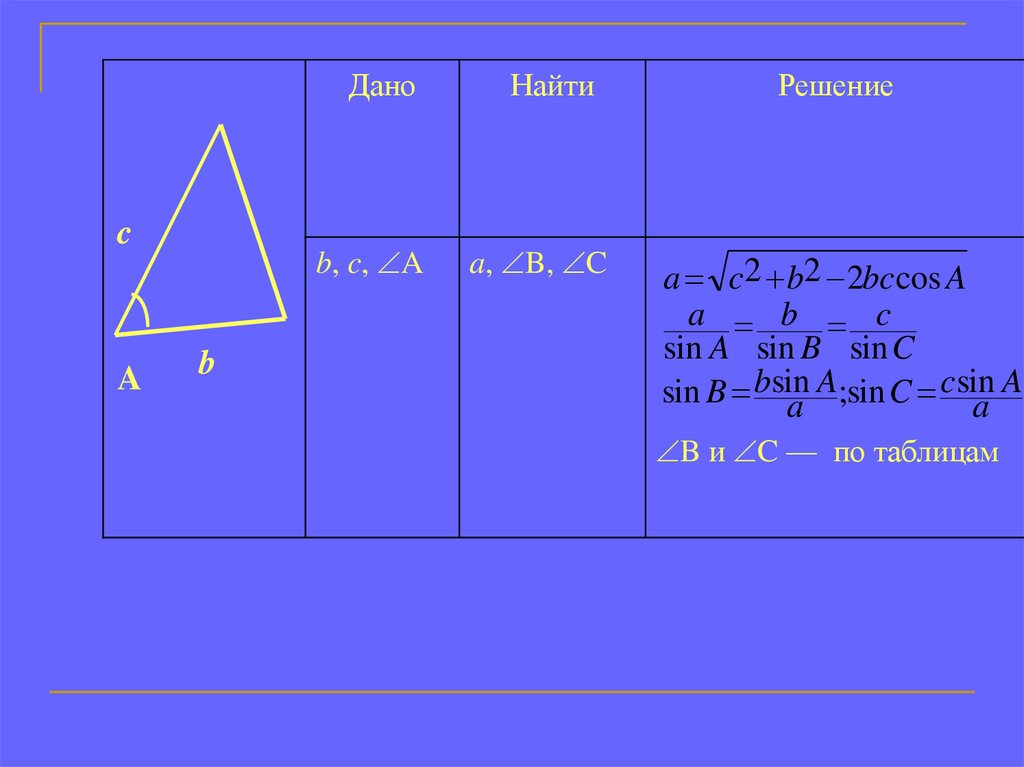
Дано
c
A
b, c, A
b
Найти
a, B, C
Решение
a c2 b2 2bc cos A
a b c
sin A sin B sin C
A;sin C csin A
sin B bsin
a
a
B и C — по таблицам

9.

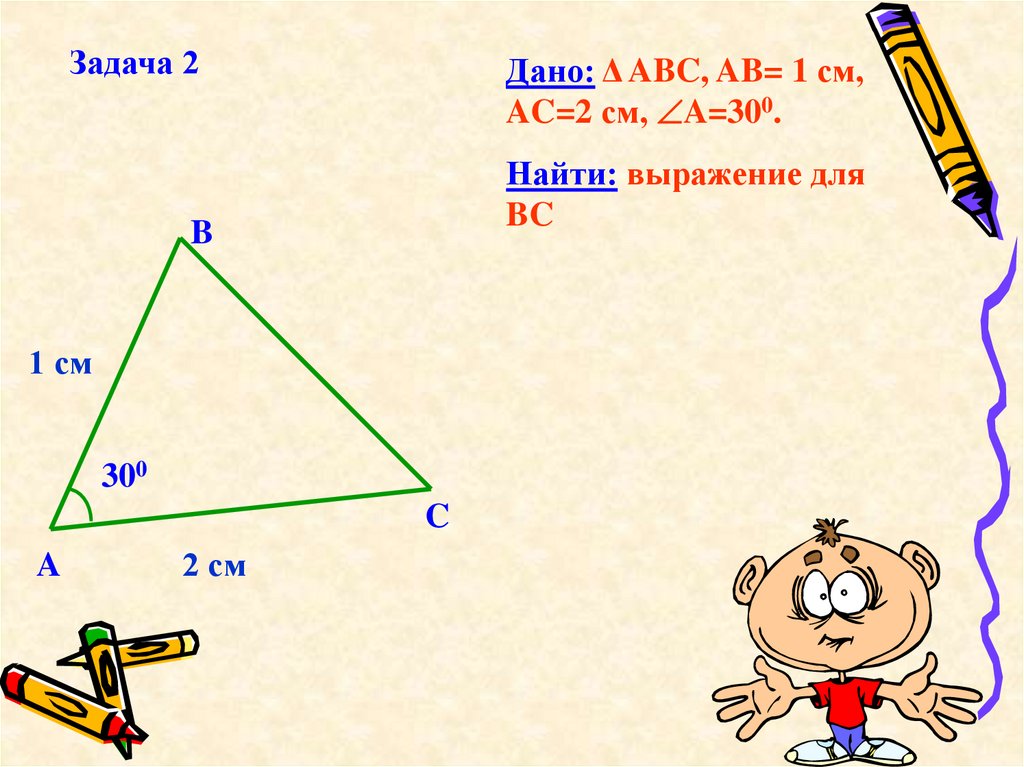
Задача 2
Дано: Δ ABC, AB= 1 см,
AC=2 см, A=300.
Найти: выражение для
BC
B
1 см
300
C
A
2 см

10.

Ответ: по теореме косинусов
BC2=AB2+AC2 – 2AB∙AC ∙cos 300
BC2= 1 4 4 3
2
BC=
5 2 3

11.

Дано
a, b, c,
c
a
b
Найти
Решение
A , B, C
a 2 c2 b2 2bc cos A
2 c2 a2
b
cos A
2bc
a b c
sin A sin B sin C
A;
sin B bsin
a
A
sin C csin
a
A , B, C — по
таблицам
или C= 1800– ( A
+ B)

12.

Задача 3
Дано: Δ ABC, AB= 1 см,
BC= 2 см, AC= 3 см
Найти: выражение для
B
B
2 см
1 см
A
3 см
C

13.

Ответ: по теореме косинусов
AC2=AB2 + BC2 – 2AB∙BC∙ cos B
2
2
2
AB
BC
AC
cos B=
cos B=
B=600
2 AB BC
1 4 3 1
4
2

14.

Дано
c
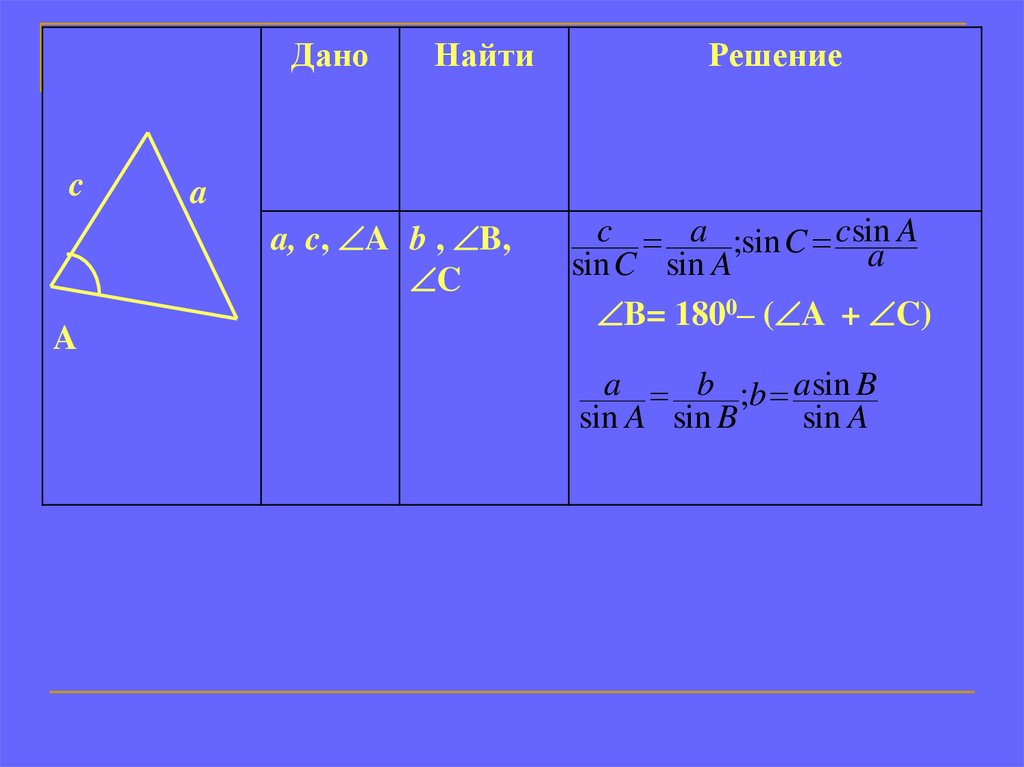
Найти
a
a, c, A b , B,
C
A
Решение
c a ;sin C csin A
a
sin C sin A
B= 1800– ( A + C)
a b ;b asin B
sin A sin B
sin A

15.

Задача 4
Дано: Δ OPR, OP=
см. 3
2
см , PR =
Найти: выражение для R
P
3
см
2 см
600
O
R

16.

Ответ: по теореме синусов
PR
OP
sin O sin R
3
2
0
sin 60
sin R
3
2
3 sin R
2
sin R 1
R=900

17.

№ 1037
C
72042′
B
12030′
70 м
A