Искусство отгадывать числа

1.

2.

Целью данной работы является исследовать, что же лежит в основе задачи
«Искусство отгадывать числа».
Гипотезой исследования стало предположение, что в основе задачи
«Искусство отгадывать числа» лежит уравнение.
Для достижения поставленной цели необходимо решить следующие задачи:
1) изучить литературу по данному вопросу;
2) найти все виды уравнений, изучаемые в школьном учебнике Н. Я.
Виленкина «Математика 6»;
3) исследовать задачу «Искусство отгадывать числа»;
4) разработать памятку «Решаем уравнения на 5».
Методы:
- поисковый метод с использованием научной и учебной литературы;
-исследовательский метод при определении видов уравнений,
изучаемые в школьном учебнике Н. Я. Виленкина «Математика 6»;
- практический метод при разработки памятки «Решаем уравнения на 5».

3.

«Мне приходится делить свое время
между политикой и уравнениями.
Однако уравнение, по – моему,
гораздо важнее, потому что
политика
существует
только
для данного момента, а уравнения
будут существовать вечно».
А. Эйнштейн.

4.

Математический папирус Ринда.
1550 г. до н.э. Содержит решение 84 задач,
вычисления площадей и объемов.

5.

Древнеегипетская запись уравнения
2 1 1
х ( 1) 37
3 2 7

6.

Задача из папируса Ахмеса
Задача: «Количество и его четвертая часть дают
вместе 15»
В настоящее время для ее решения составляют
уравнение х 1 х 15. Решая его, мы находим
4
ответ: 12

7.

Ал-ХОРЕЗМИ Мухаммед бен-Муса (783-850).

8.

Леонардо Пизанский
(Фибоначчи)

9.

Страница из Книги абака

10.

11.

Уравнение – равенство, содержащее букву, значение
которой надо найти.
Выражение слева от знака равенства называется левой
частью уравнения, а справа от знака равенства – правой
частью уравнения.
Это значение неизвестного, называется корнем уравнения
или решением уравнения.
Корнем уравнения называется число, подстановка
которого вместо буквы превращает уравнение в верное
равенство.
Решить уравнение – значит найти все его корни (или
убедиться, что это уравнение не имеет ни одного корня).

12.

13.

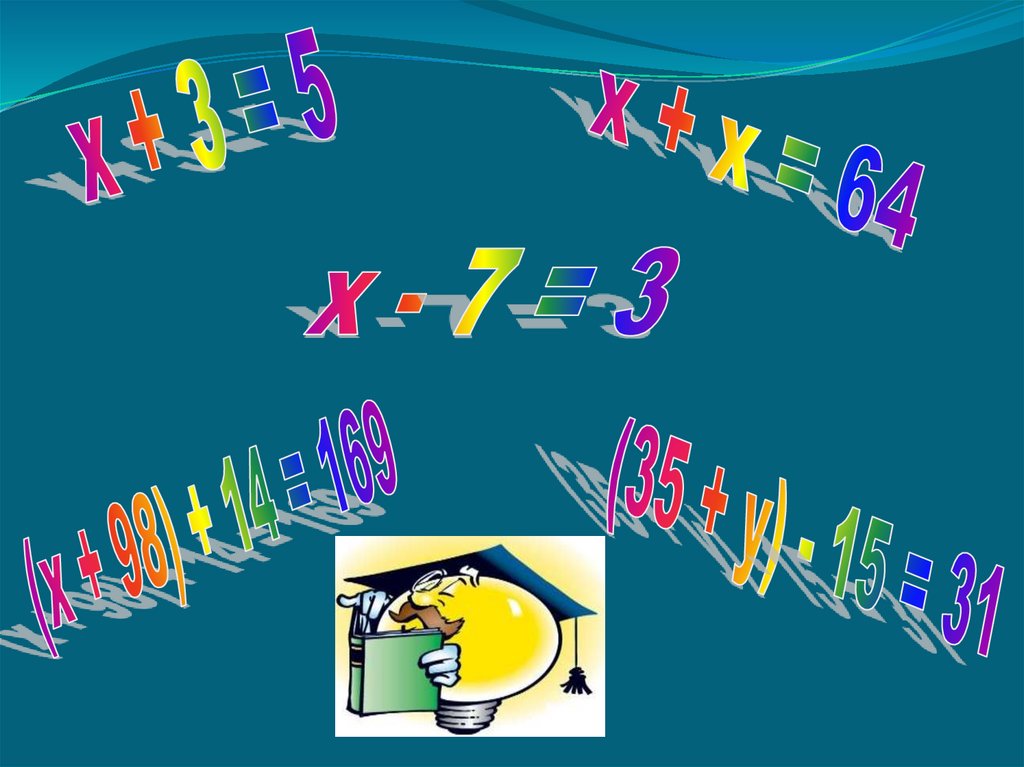
Все виды уравнений, изучаемые в школьном учебнике
Н. Я. Виленкина «Математика 6»
№
Виды уравнений
Примеры
1
x–a=b
x–8=1
2
x+a=b
3
a–x=b
4
a+x=b
5
(x + a) – b = c
(x + 15) – 8 = 17
6
(a + x) – b = c
(24 + x) – 21 = 10
7
(a – x) + b = c
(45 – x) + 18 = 58
15 – x = 9

14.

8
(x – a) + b = c
(x – 35) + 12 = 32
9
a– (x + b) = c
56 – (x + 12) = 24
10
a – (x – b) = c
16,1 – (x – 3,8) = 11,3
11
(x – a) – b = c
(x – 87) – 27 = 36
12
a – (b + x) = c
25,34 – (2,7 + x) = 15,34
13
ax + bx = c
x + x = 64
14
a + bx + cx + dx = f
58 + x + x + x = 58
15
ax +b = cx – d
x +2 = x – 1
16
a – bx = c + dx
27 – x = 27 + x
17
a + x + 2 = 15 + x – 3
10 + x + 2 = 15 + x – 3

15.

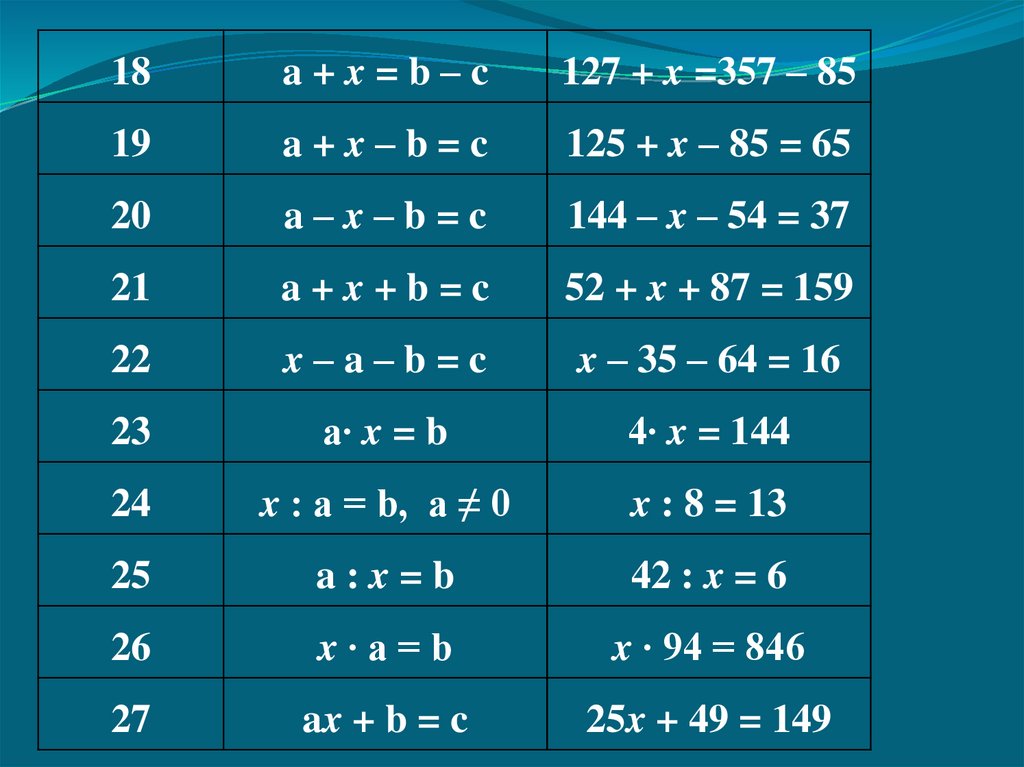
18
a+x=b–c
127 + x =357 – 85
19
a+x–b=c
125 + x – 85 = 65
20
a–x–b=c
144 – x – 54 = 37
21
a+x+b=c
52 + x + 87 = 159
22
x–a–b=c
x – 35 – 64 = 16
23
a∙ x = b
4∙ x = 144
24
x : a = b, a ≠ 0
x : 8 = 13
25
a:x=b
42 : x = 6
26
x∙a=b
x ∙ 94 = 846
27
ax + b = c
25x + 49 = 149

16.

28
a + bx = c
13 + 10x = 163
29
ax – b = c
9x – 54 = 162
30
a – bx = c
181 – 8x = 45
31
(x – a) ∙ b = c
(x – 12) ∙ 8 = 56
32
a ∙ (x + b) = c
24 ∙ (x + 9) = 288
33
(x + a) : b = c, b ≠ 0
(x + 25) : 8 = 16
34
a : (x – b) = c
295,1 : (x – 3) = 13
35
a:x+b=c
44 : x + 9 = 20
36
a∙ x = a : x
15 ∙ x = 15 : x
37
x+x=x∙x
x+x=x∙x

17.

38
x ∙ a = x : a, a ≠ 0
x ∙ 10 = x : 10
39
(a + x) ∙b = c
(38 + x) ∙12 = 840
40
a – bx = c
160 – 2x = 40
41
ax – bx = c
15x – 8x =714
42
ax + bx + cx = d
4x + 5x + x = 1200
43
ax + bx – cx = d
6x + 3x – x = 6400
44
ax + bx + c = d
3x + 7x + 18 = 178
45
ax – bx + c = d
6x – 2x + 25 = 65
46
ax + bx – c = d
7x + 6x – 13 = 130
47
ax – bx – c = d
21x – 4x – 17 = 17

18.

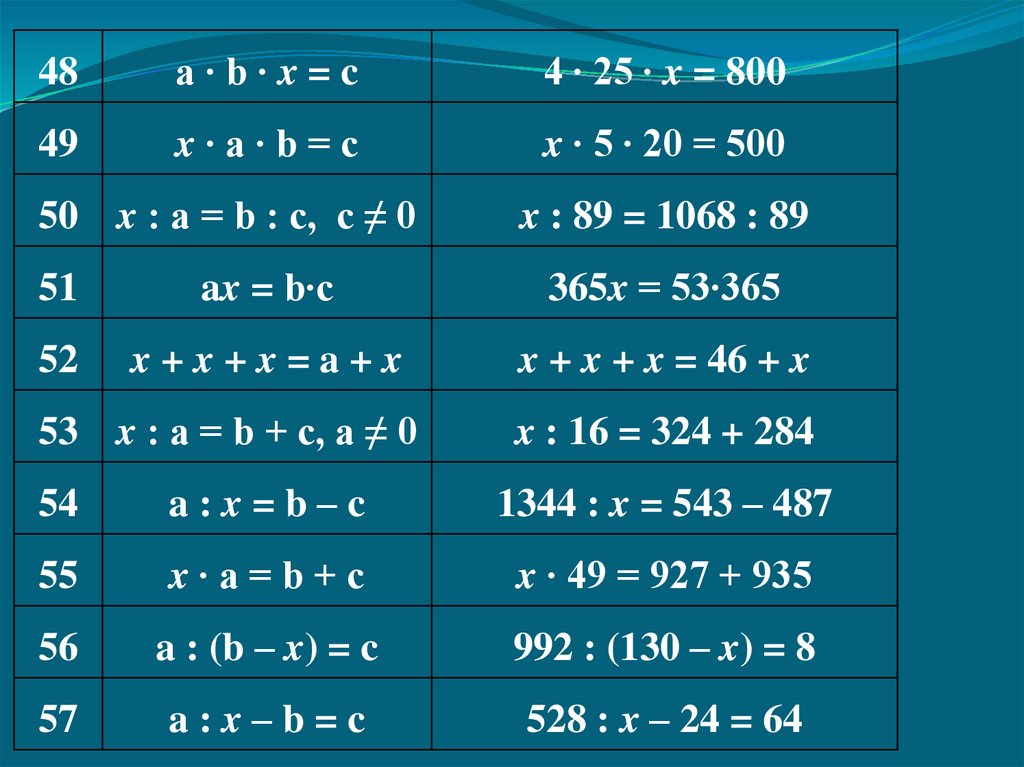
48
a∙b∙x=c
4 ∙ 25 ∙ x = 800
49
x∙a∙b=c
x ∙ 5 ∙ 20 = 500
50 x : a = b : c, c ≠ 0
x : 89 = 1068 : 89
51
ax = b∙c
365x = 53∙365
52
x+x+x=a+x
x + x + x = 46 + x
53 x : a = b + c, a ≠ 0
x : 16 = 324 + 284
54
a:x=b–c
1344 : x = 543 – 487
55
x∙a=b+c
x ∙ 49 = 927 + 935
56
a : (b – x) = c
992 : (130 – x) = 8
57
a:x–b=c
528 : x – 24 = 64

19.

58
a : b + x = c, b ≠ 0
88880 : 110 + x = 809
59
a + x : b = c, b ≠ 0
6871 + x : 121 = 7000
60
a+b:x=c
3810 + 1206 : x = 3877
61
x + a : b = c, b ≠ 0
x + 12705 : 121 = 105
62
(ax + bx) ∙ c = d
(3x + 5x) ∙ 18 = 144
63
(ax – bx) : c = d, c ≠ 0
(7x – 3x) : 8 = 17
64
a : (bx – cx) = d
48 : (9x – x) = 2
65
x : x =a
x : x =1
66
a ∙ (x – b) = c
975 ∙ (x – 361) = 14625
67
a(b + x) + d = c
3(25 + x) + 15 = 135

20.

68
a–x=b–c
69
a–b+x=c
70
71
, b≠0
(ax + b) ∙ c = d
72 x : a = b – c, a ≠ 0
(27x + 11) ∙ 315 = 11970
x : 27 = 2467 – 1867
73
x+a=b+c
74
a – (b – x) = c
34,2 – (17,9 – x) = 22
75
x–a=b+c
x – 6,8 = 8,7 + 6,4
76
a–x+b=c
10 – x + 4,3 = 10,7
77
x2 = x
x2 = x

21.

78
x3 = x
x3 = x
79
x2 = x 3
x2 = x3
80
(x – a) : b = c, b ≠ 0
(x – 1,2) : 0,6 = 21,1
81
a ∙ (b + x) = c
4,2 ∙ (0,8 + x) = 8,82
82
ax – bx – cx + d = f
5,6x – 2x – 0,7x + 2,65 = 7
83
ax – (bx + c) = d
4,7x – (2,5x + 12,4) = 1,9
84
(a – x) ∙ b = c
(8,3 – x) ∙ 4,7 = 5,64
85
(ax – bx) ∙ c = d
(7x – 2x) ∙ 8 = 80
86 (ax + x) : b = c, b ≠ 0
(15x + x) : 4 = 3

22.

87
88
(ax – bx) ∙c : d : f = 0,
d ≠ 0, f ≠ 0
a ∙ (bx – cx) : d : f = 0, d
≠ 0, f ≠ 0
(0,87x – 0,66x) ∙10 : 2 : 3 = 0
10 ∙ (1,37x – 0,12x) : 5 : 8 = 0
89
a=a+x
45 = 45 + x
90
0=a–х
0 = 45 – х
Где a, b, c, d, f – натуральные числа, обыкновенные или
десятичные дроби. x – корень уравнения.

23.

На родном языке
На языке алгебры
Задумайте число,
x
x+2
3x + 6
3x + 1
2x + 1
4x + 2
4x + 1
прибавьте 2,
умножьте результат на 3,
вычтите 5,
вычтите задуманное число,
умножьте на 2,
вычтите 1

24.

В процессе выполненной исследовательской работы в соответствии с ее
целью и задачами получены следующие выводы и результаты.
1. На основе изученной литературы по данной теме, открыла для себя много
интересного и нового об уравнениях, чего не могла прочитать в учебнике.
Например, узнала о том, что ещё в древности люди пользовались ими, не
зная, что это – уравнения. В наше время невозможно представить себе
решение, как простейших, так и сложных задач не только в математике, но и
в других науках, без применения решения уравнений.
2. Выполненный обзор школьного учебника Н. Я. Виленкина «Математика
6», показал, что в учебнике встречаются 90 видов уравнений.
3. Исследовав задачу «Искусство отгадывать числа», выяснила, что в основе
задачи лежит уравнение.
4. Подготовлена и разработана памятка «Решаем уравнения на 5».