Математическая статистика и ее роль в медицине

1.

Математическая
статистика и ее
роль в медицине

2.

задание
10.2. В результате испытания случайная величина X
приняла следующие значения: 11, 13, 18, 22, 24,
12, 23, 15, 18, 17, 12, 18, 19, 20, 12, 22, 16, 17, 14,
20, 21, 25, 27, 19.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

Математическая статистика и ее связь с теорией вероятности

14.

Пример 10.1. Ежедневное количество студентов, посещающих
методический кабинет на протяжении ряда дней, следующее:
15, 17, 16, 18, 20, 21, 18, 17, 20, 15, 18, 17, 16, 19, 17, 16, 18, 19, 18, 19.
Составить статистическое распределение выборки. Решение. В первой
строке табл. 10.1 укажем встречающиеся значения посещений, во
второй - количество таких значений и, наконец, в третьей относительную частоту этих значений. ᐊ
Таблица 10.1. Статистическое распределение выборки в табличном
виде для примера 10.1
Р (вероятность появления хi)
n количество числовых данных (чисел) в ряду. В примере 10.1 n=20.
m1 =2 т.к. число 15 встречается 2 раза.
Для графического изображения статистического распределения строят
полигоны или гистограммы.

15.

16.

17.

18.

19.

20.

21.

22.

23.

Графическое изображение выборки
Гистограмма и полигон

24.

Пример 10.1. Ежедневное количество студентов, посещающих
методический кабинет на протяжении ряда дней, следующее:
15, 17, 16, 18, 20, 21, 18, 17, 20, 15, 18, 17, 16, 19, 17, 16, 18, 19, 18, 19.
Составить статистическое распределение выборки. Решение. В первой
строке табл. 10.1 укажем встречающиеся значения посещений, во
второй - количество таких значений и, наконец, в третьей относительную частоту этих значений. ᐊ
Таблица 10.1. Статистическое распределение выборки в табличном
виде для примера 10.1
n количество числовых данных (чисел) в ряду. В примере 10.1 n=20.
m1 =2 т.к. число 15 встречается 2 раза.
Для графического изображения статистического распределения строят
полигоны или гистограммы.

25.

Определение
Гистограммой называется график, по оси абсцисс которого отложены
границы классов, а по оси ординат - их частота.
Для построения гистограммы весь диапазон измеряемой величины (от
минимального до максимального) разбивается на равные интервалы,
называемые классами. Ширину интервала можно определить по
формуле Стерджеса:
где h - ширина интервала; xmax, xmin - максимальное и минимальное
значения выборочной величины соответственно; n - количество
выборочных данных.

26.

Получение нормированных гистограмм позволяет сравнивать
гистограммы, построенные на одних и тех же границах классов,
но имеющих различный объем выборки.

27.

Пример 10.2. Построить гистограмму для примера 10.1. Решение.
Составим для начала табл. 10.2. А затем построим гистограмму (рис.
10.1). ᐊ
Таблица 10.2. Данные для построения гистограммы
Полигон частот можно получить из гистограммы путем соединения
срединных значений классов (см. рис. 10.1). График полигона частот
(или относительных частот) легко построить и по статистическому распределению. На оси абсцисс, из точек xi проводят перпендикуляры
высотой mi/n и соединяют ломаной линией.

28.

При неограниченном увеличении числа наблюдений и увеличении
количества классов ширина прямоугольников гистограммы будет
уменьшаться, и середины верхних концов прямоугольников сольются в
одну сплошную плавную линию, которая в пределе станет графиком
плотности вероятности, характеризующим распределение
генеральной совокупности.
Построение полигонов и гистограмм позволяет произвести первичный
анализ экспериментальных данных, а именно: по форме гистограммы сделать предположение о законе распределения случайной
величины; выявить наиболее часто встречающиеся значения
исследуемой величины и разброс или отклонение относительно этого
значения.

29.

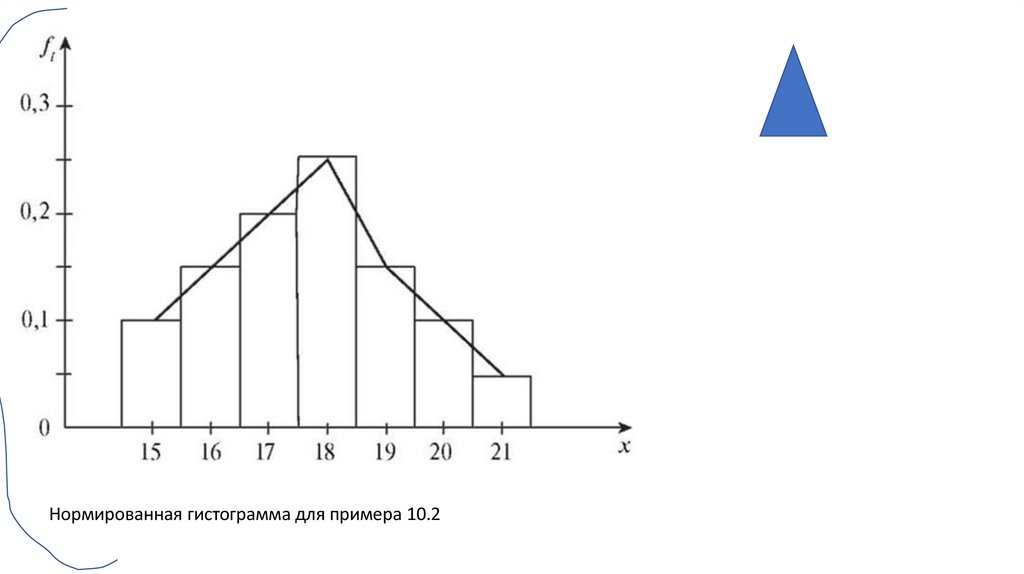
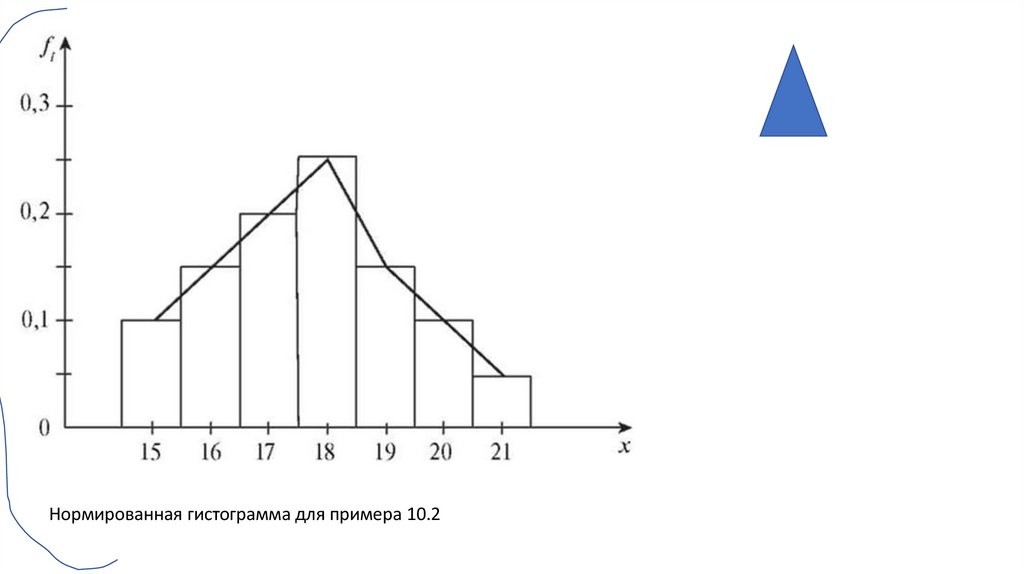
Нормированная гистограмма для примера 10.2

30.

Графические изображения, применяемые для более наглядного
изображения статистических данных, называются диаграммами.
Наиболее часто используются следующие виды диаграмм: линейные,
столбцовые и круговые.
Линейная диаграмма представляет собой прямоугольную систему
координат. По оси абсцисс обычно откладывают равные промежутки
времени, а по оси ординат - значения того или иного статистического
показателя в соответствующем масштабе.
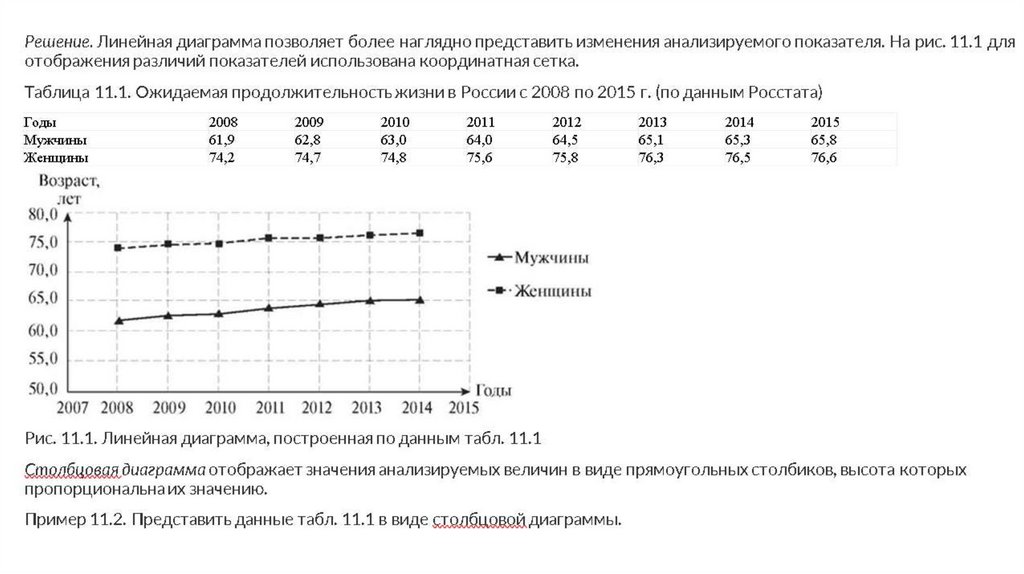
Пример 11.1. Представить в виде линейной диаграммы ожидаемую
продолжительность жизни в России с 2008 по 2015 г. Данные
приведены в табл. 11.1

31.

32.

33.

34.

35.

36.

37.

Выборка и выборочное среднее

38.

39.

40.

41.

n количество чисел
Выборочная
средняя
Выборочная дисперсия
Ошибка
выборочной средней
= 2
1,4

42.

Пример 10.4. Из генеральной совокупности извлечена выборка (табл. 10.3). Найти оценки математического
ожидания и дисперсии.
Таблица 10.3. Выборка для примера 10.4

43.

ИНТЕРВАЛЬНАЯ ОЦЕНКА.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ
И ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ
В некоторых случаях представляет интерес не получение
точечной оценки неизвестного параметра генеральной
совокупности, а определение некоторого интервала, в котором
может находиться этот параметр с заданной вероятностью.
Интервальное оценивание более эффективно при малом числе
наблюдений, когда точечная оценка мало надежна.

44.

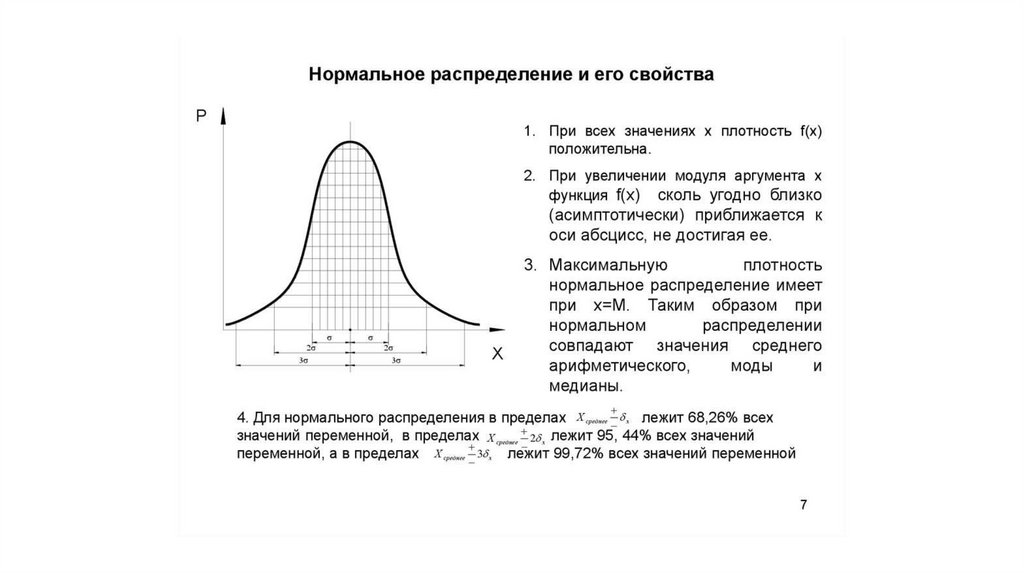
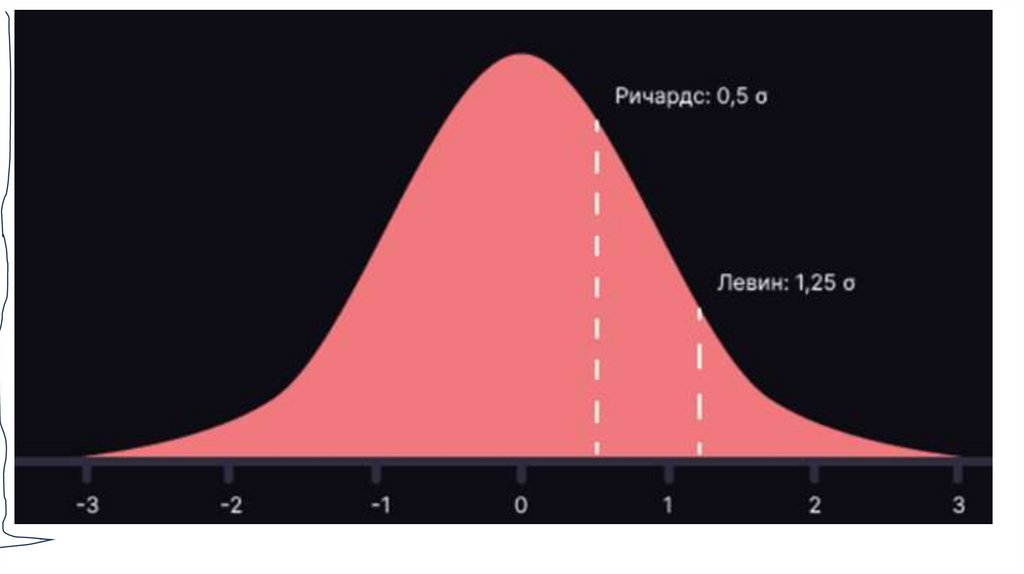
Вероятность, с которой гарантируется попадание параметра генеральной совокупности внутрь
доверительного интервала, называются доверительной. Чаще в качестве доверительных используются
уровни вероятности: P1 = 0,95; P2 = 0,99 и P3 = 0,999. Это
означает, что параметр генеральной совокупности попадет в
указанный интервал в первом случае в 95 случаях из 100, во
втором - в 99 случаях из 100 и в третьем случае - в 999 случаях
из 1000.
В некоторых случаях указывается не доверительная
вероятность, а вероятность обратных случаев, когда параметр
не попадает в указанный интервал. Вероятность таких
маловероятных случаев называется уровнем значимости α и
равна:
α = 1 - P.
следующие

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

Построение гистограммы

55.

10.3. СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ (ВАРИАЦИОННЫЙ РЯД). ГИСТОГРАММА. ПОЛИГОН
В ходе экспериментов исследователь получает набор числовых данных, отражающих результаты измерений или
наблюдений исследуемых объектов. Совокупность этих числовых данных, представленных в виде
последовательности результатов наблюдений x1, x2, ..., xn есть выборка из генеральной совокупности. Основная
задача первичного статистического анализа состоит в том, чтобы по имеющимся экспериментальным данным
охарактеризовать исследуемую генеральную совокупность небольшим числом параметров.
Если полученные данные расположить в порядке убывания или возрастания числовых значений исследуемого
признака, то такой ряд чисел будет называться вариационным рядом.
В том случае, когда среди числовых данных есть одинаковые значения, их можно представить в виде таблицы. В
первой строке таблицы указываются значения признака (варианты), а во второй - абсолютные или относительные
частоты их встречаемости. Такое представление вариационного ряда еще называют статистическим распределением.
Определение
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или
относительных частот встречаемости.

56.

Пример 10.1. Ежедневное количество студентов, посещающих
методический кабинет на протяжении ряда дней, следующее:
15, 17, 16, 18, 20, 21, 18, 17, 20, 15, 18, 17, 16, 19, 17, 16, 18, 19, 18, 19.
Составить статистическое распределение выборки. Решение. В первой
строке табл. 10.1 укажем встречающиеся значения посещений, во
второй - количество таких значений и, наконец, в третьей относительную частоту этих значений. ᐊ
Таблица 10.1. Статистическое распределение выборки в табличном
виде для примера 10.1
n количество числовых данных (чисел) в ряду. В примере 10.1 n=20.
m1 =2 т.к. число 15 встречается 2 раза.
Для графического изображения статистического распределения строят
полигоны или гистограммы.

57.

Определение
Гистограммой называется график, по оси абсцисс которого отложены
границы классов, а по оси ординат - их частота.
Для построения гистограммы весь диапазон измеряемой величины (от
минимального до максимального) разбивается на равные интервалы,
называемые классами. Ширину интервала можно определить по
формуле Стерджеса:
где h - ширина интервала; xmax, xmin - максимальное и минимальное
значения выборочной величины соответственно; n - количество
выборочных данных.

58.

Зная ширину интервала, определяют количество интервалов.
Однако эта формула носит эмпирический характер, и на практике
количество интервалов выбирают в пределах 7-12. После выбора
количества интервалов устанавливают границы классов (Сi.) и
срединные значения
классов ( Cī ), где
- середина i-го класса, i = 1, 2,..., k -количество классов.
Затем определяют mi - количество значений выборочных данных,
которые попадают в тот или иной класс. После просмотра всех
выборочных данных по значениям mi строят гистограмму. По этой
гистограмме можно построить нормированную гистограмму, в которой
каждое значение m. заменяется значением fi = mi/n.

59.

Получение нормированных гистограмм позволяет сравнивать
гистограммы, построенные на одних и тех же границах классов,
но имеющих различный объем выборки.

60.

Пример 10.2. Построить гистограмму для примера 10.1. Решение.
Составим для начала табл. 10.2. А затем построим гистограмму (рис.
10.1). ᐊ
Таблица 10.2. Данные для построения гистограммы
Полигон частот можно получить из гистограммы путем соединения
срединных значений классов (см. рис. 10.1). График полигона частот
(или относительных частот) легко построить и по статистическому распределению. На оси абсцисс, из точек xi проводят перпендикуляры
высотой mi/n и соединяют ломаной линией.

61.

При неограниченном увеличении числа наблюдений и увеличении
количества классов ширина прямоугольников гистограммы будет
уменьшаться, и середины верхних концов прямоугольников сольются в
одну сплошную плавную линию, которая в пределе станет графиком
плотности вероятности, характеризующим распределение
генеральной совокупности.
Построение полигонов и гистограмм позволяет произвести первичный
анализ экспериментальных данных, а именно: по форме гистограммы сделать предположение о законе распределения случайной
величины; выявить наиболее часто встречающиеся значения
исследуемой величины и разброс или отклонение относительно этого
значения.

62.

Нормированная гистограмма для примера 10.2

63.

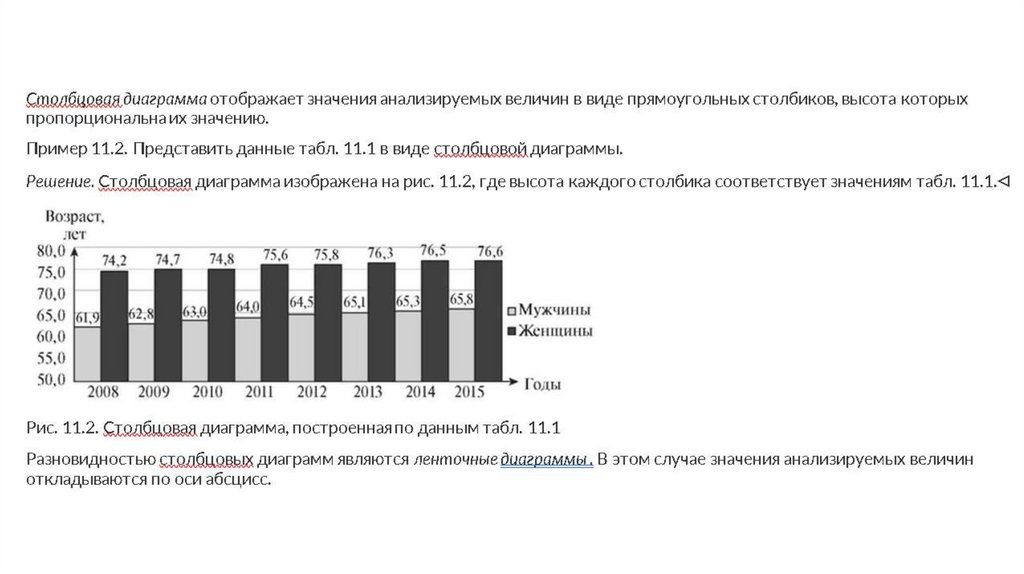
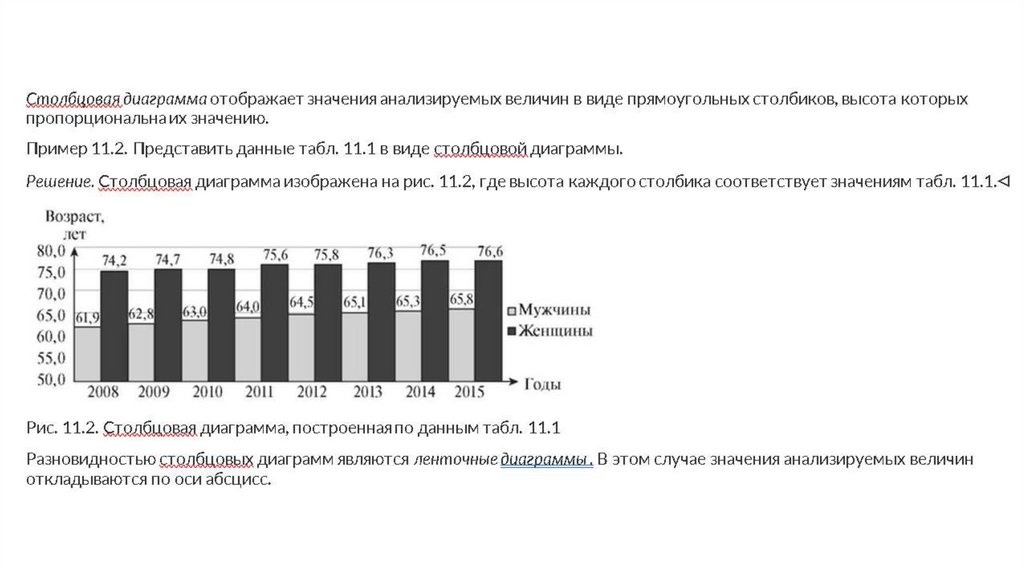
Графические изображения, применяемые для более наглядного
изображения статистических данных, называются диаграммами.
Наиболее часто используются следующие виды диаграмм: линейные,
столбцовые и круговые.
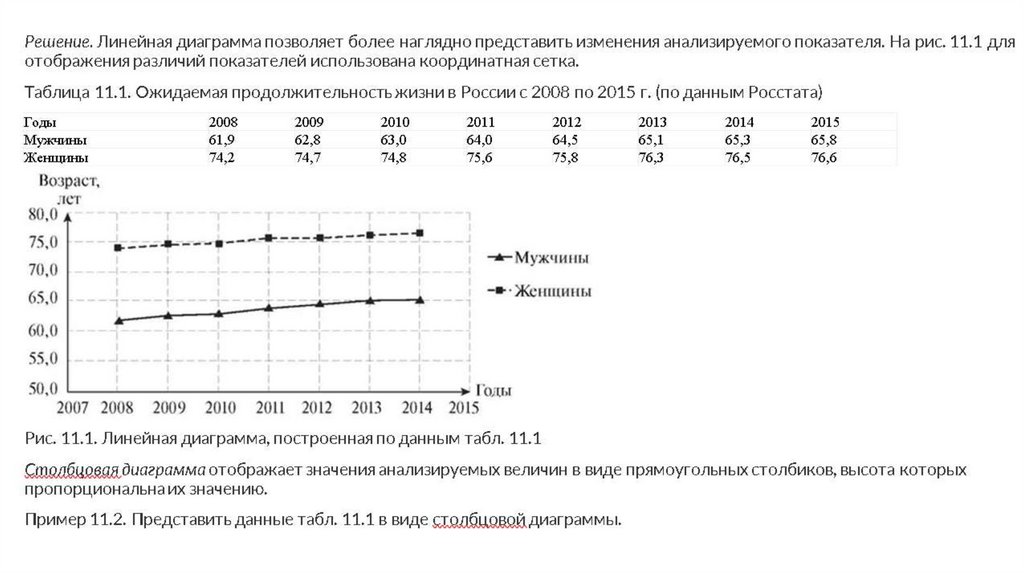
Линейная диаграмма представляет собой прямоугольную систему
координат. По оси абсцисс обычно откладывают равные промежутки
времени, а по оси ординат - значения того или иного статистического
показателя в соответствующем масштабе.
Пример 11.1. Представить в виде линейной диаграммы ожидаемую
продолжительность жизни в России с 2008 по 2015 г. Данные
приведены в табл. 11.1