Обучающая программа решению задач учащихся на геометрический смысл производной

1.

Обучающая программа решению задач
учащихся на геометрический смысл
производной
Учитель математики МБОУ СОШ№2
г. Салехард
Кривокорова Наталья Юрьевна

2.

1. В чем состоит геометрический смысл
производной ?
f ´(x₀) = tg α = к
2. В любой ли точке графика можно провести касательную? Какая
функция
значениеназывается дифференцируемой в точке?
производной в
тангенс угла
угловой
наклона
точке x₀
касательной
к углом к коэффициент
3. Касательная наклонена
под тупым
положительному
касательной
направлению оси ОХ. положительно
Следовательно, • • • . му направлению
оси ОХ
4. Касательная наклонена под острым углом к положительному
направлению оси ОХ.
Следовательно, • • • .
5. Касательная параллельна оси ОХ, либо с ней совпадает.
Следовательно, • • • .
ГРАФИК

3.

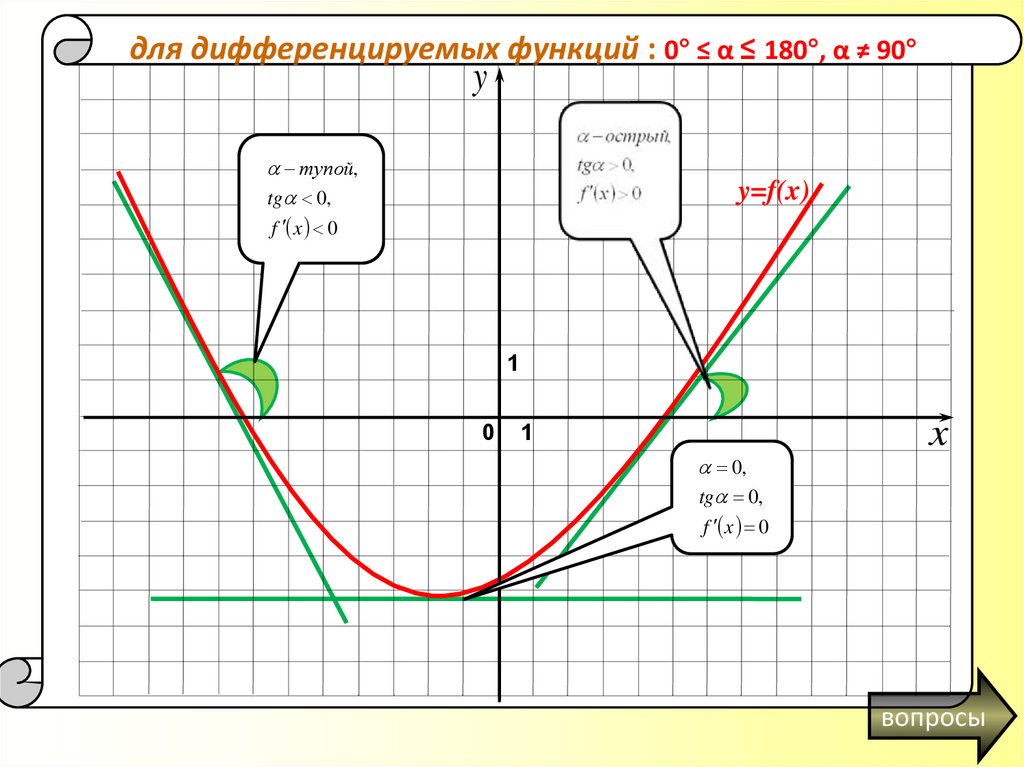
для дифференцируемых функций : 0° ≤ α ≤ 180°, α ≠ 90°
y
тупой,
tg 0,
y=f(x)
f x 0
1
0
1
0,
tg 0,
x
f x 0
вопросы

4.

Геометрический смысл производной
Задачи с графическим заданием функции
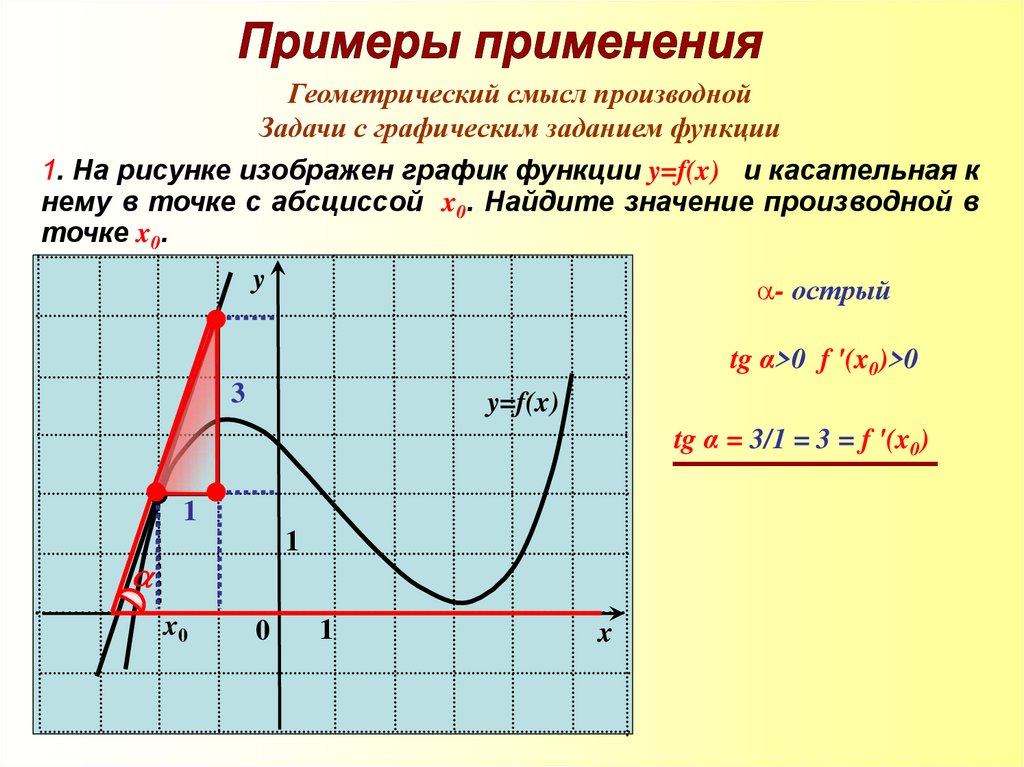
1. На рисунке изображен график функции y=f(x) и касательная к
нему в точке с абсциссой x0. Найдите значение производной в
точке x0.
y
- острый
tg α>0 f '(x0)>0
3
y=f(x)
tg α = 3/1 = 3 = f '(x0)
1
1
x0
0
1
x

5.

Геометрический смысл производной
Задачи с графическим заданием функции
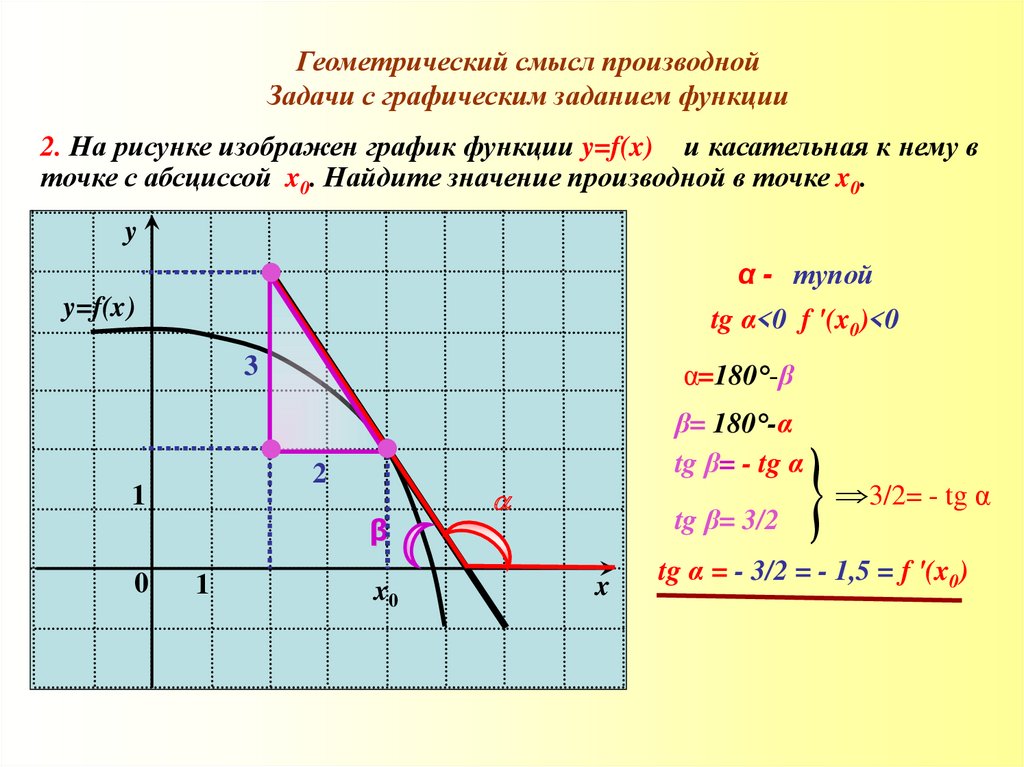
2. На рисунке изображен график функции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной в точке x0.
y
α - тупой
y=f(x)
tg α<0 f '(x0)<0
3
α=180°-β
β= 180°-α
tg β= - tg α
2
1
β
0
1
x0
tg β= 3/2
x
3/2= - tg α
tg α = - 3/2 = - 1,5 = f '(x0)

6.

Геометрический смысл производной
Задачи с графическим заданием функции
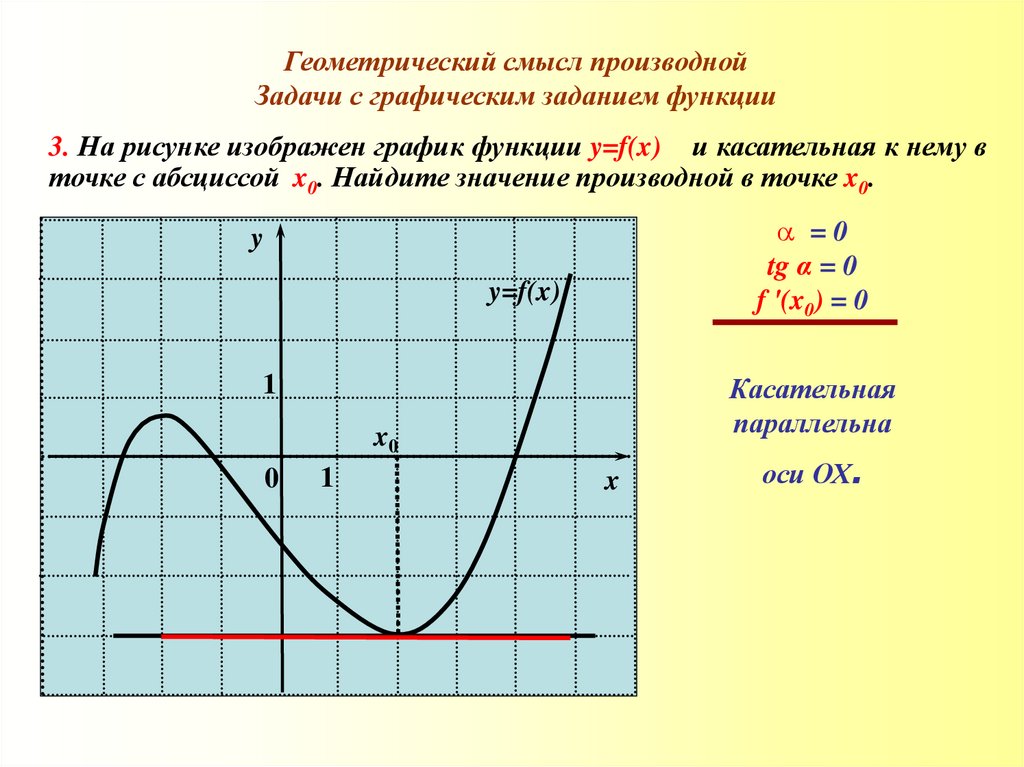
3. На рисунке изображен график функции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной в точке x0.
=0
tg α = 0
f '(x0) = 0
y
y=f(x)
Касательная
параллельна
1
x0
0
1
x
оси ОХ.

7.

Геометрический смысл производной
Задачи с графическим заданием функции
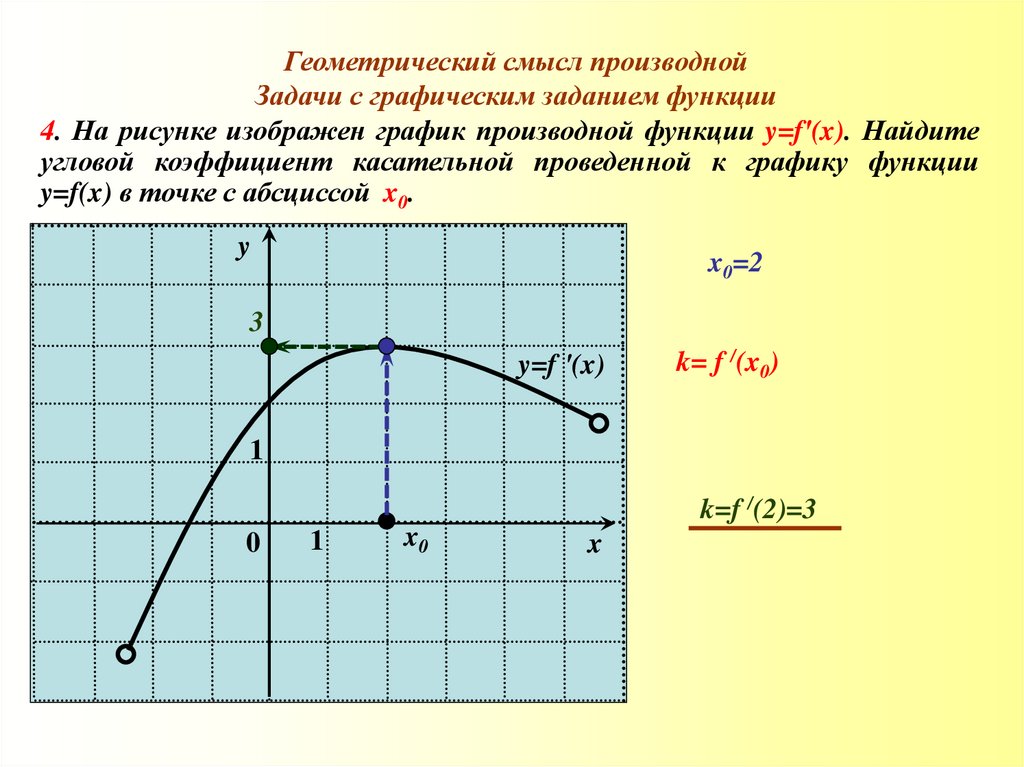
4. На рисунке изображен график производной функции y=f′(x). Найдите
угловой коэффициент касательной проведенной к графику функции
y=f(x) в точке с абсциссой x0.
y
x0=2
3
y=f '(x)
k= f /(x0)
1
k=f /(2)=3
0
1
x0
x

8.

Геометрический смысл производной
Задачи с графическим заданием функции
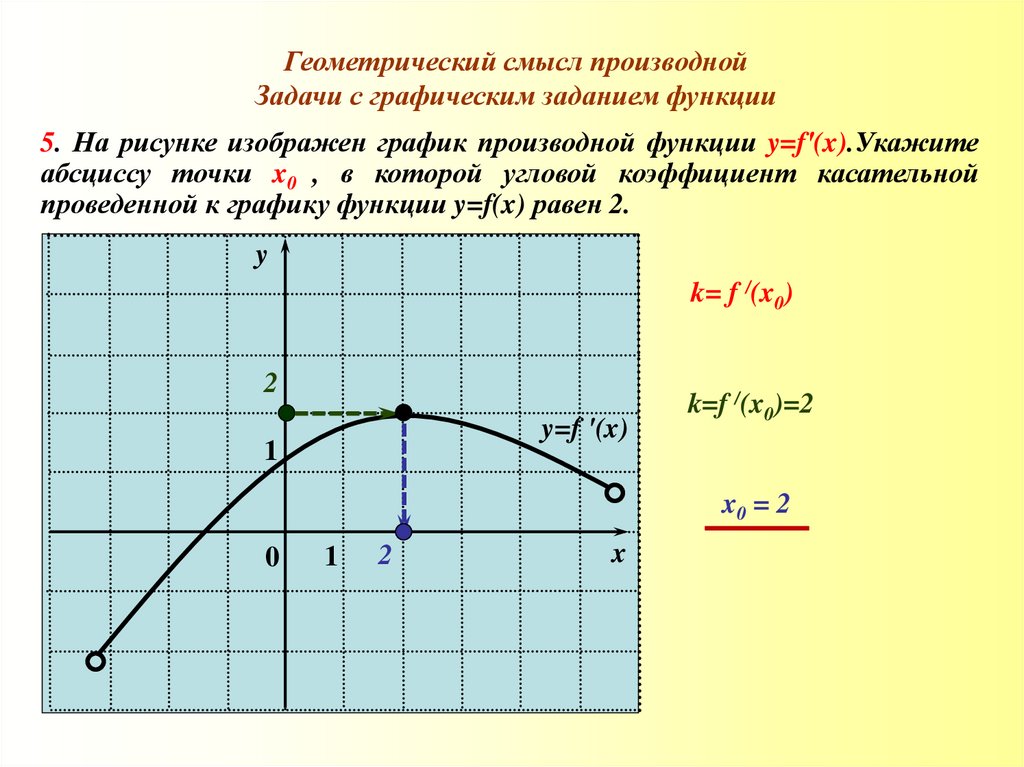
5. На рисунке изображен график производной функции y=f′(x).Укажите
абсциссу точки x0 , в которой угловой коэффициент касательной
проведенной к графику функции y=f(x) равен 2.
y
k= f /(x0)
2
y=f '(x)
1
k=f /(x0)=2
x0 = 2
0
1
2
x

9.

Геометрический смысл производной
Задачи с графическим заданием функции
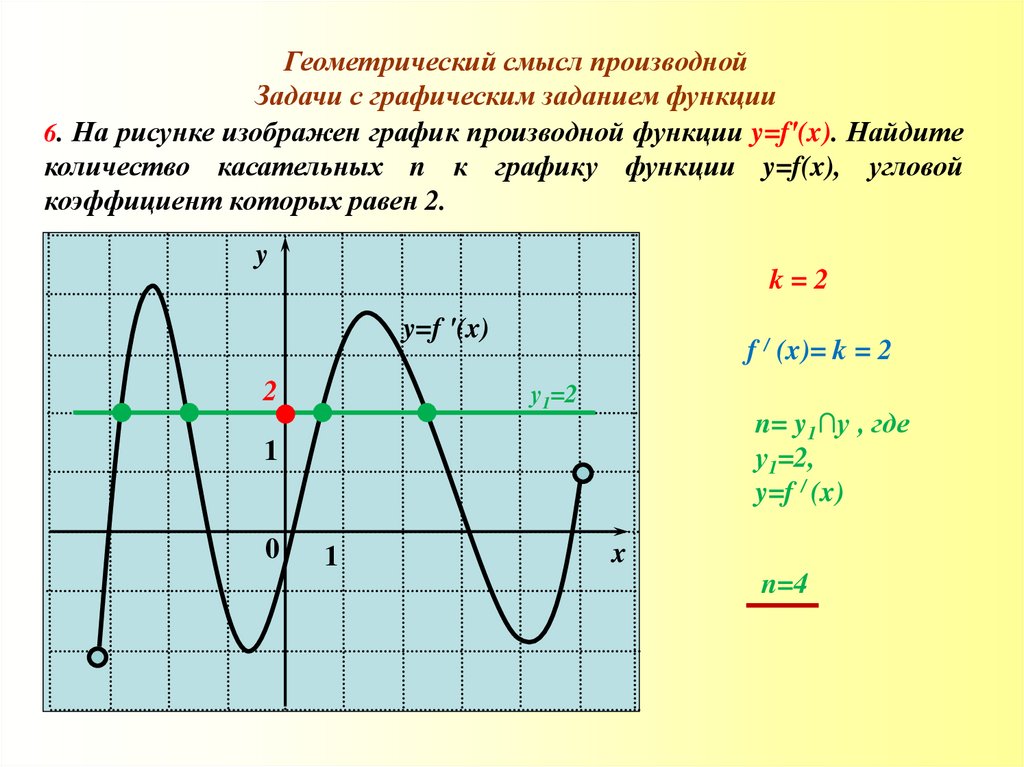
6. На рисунке изображен график производной функции y=f′(x). Найдите
количество касательных n к графику функции y=f(x), угловой
коэффициент которых равен 2.
y
k=2
y=f '(x)
f / (x)= k = 2
у1=2
2
n= y1∩y , где
у1=2,
y=f / (x)
1
0
1
x
n=4

10.

Геометрический смысл производной
Задачи с графическим заданием функции
7. На рисунке изображен график производной функции y=f′(x).
Определите абсциссу точки касательная в которой составляет с осью
OX угол в 45° .
y
tg 45°=1
k= tgα=f / (x)
k=f / (x) = tg45° = 1
1
0
1 x0
y=f '(x)
x
x0=1

11.

Геометрический смысл производной
Задачи с графическим заданием функции
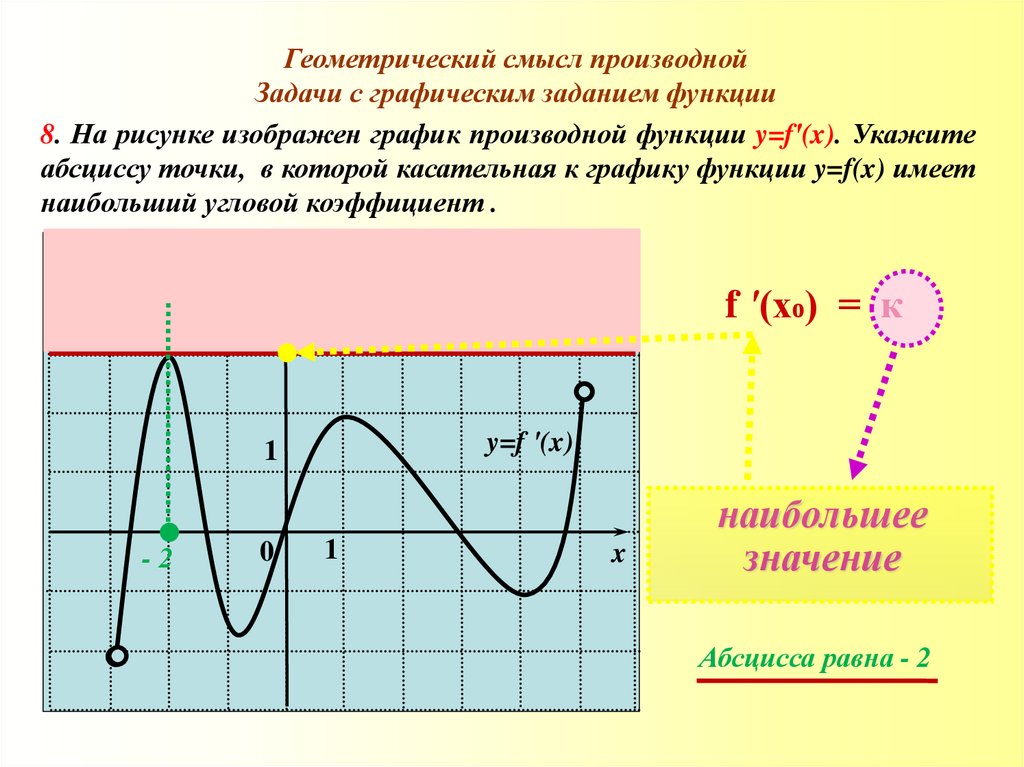
8. На рисунке изображен график производной функции y=f′(x). Укажите
абсциссу точки, в которой касательная к графику функции y=f(x) имеет
наибольший угловой коэффициент .
y
f '(x₀) = к
y=f '(x)
1
-2
0
1
x
наибольшее
значение
Абсцисса равна - 2

12.

Геометрический смысл производной
Задачи с графическим заданием функции
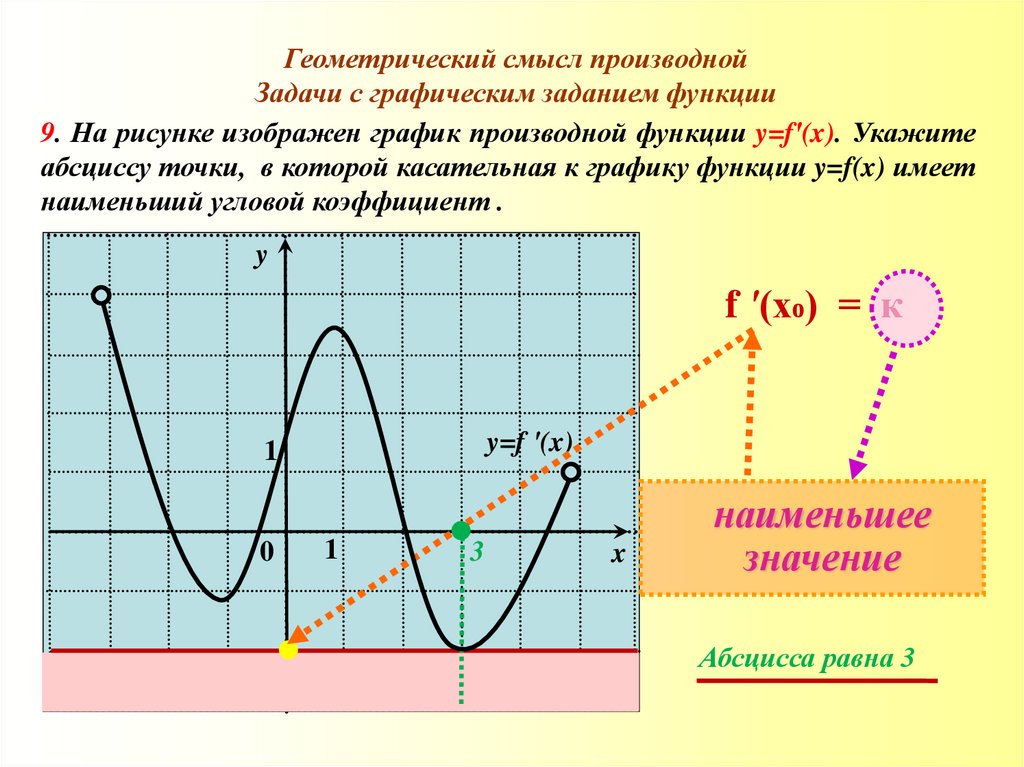
9. На рисунке изображен график производной функции y=f′(x). Укажите
абсциссу точки, в которой касательная к графику функции y=f(x) имеет
наименьший угловой коэффициент .
y
f '(x₀) = к
y=f '(x)
1
0
1
3
x
наименьшее
значение
Абсцисса равна 3

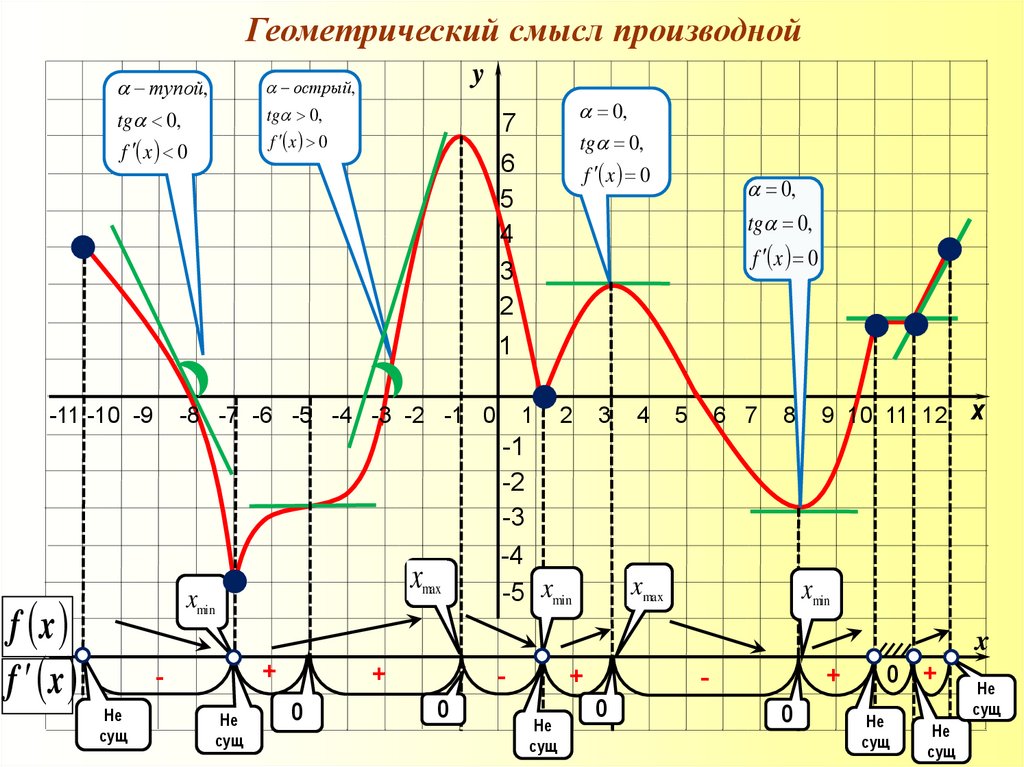
13.

Геометрический смысл производной
тупой,
tg 0,
f x 0
y
острый,
tg 0,
f x 0
0,
tg 0,
f x 0
7
6
5
4
3
2
0,
tg 0,
f x 0
1
-11 -10 -9
f x
f x
-8 -7 -6 -5 -4 -3 -2 -1 0
xmax
xmin
1
2
3
-1
-2
-3
-4
-5 xmin
4
5
6 7
8
xmax
9 10 11 12
x
xmin
x
0
0
Не
сущ
-
+
Не
сущ
+
0
Не
сущ
+
0
+
-
0 +
Не
сущ
Не
сущ
Не
сущ