Похожие презентации:
Геометрический и физический смысл производной
1.
•Цель урока: Обобщить и закрепить идеюгеометрического и физического смысла
производной.
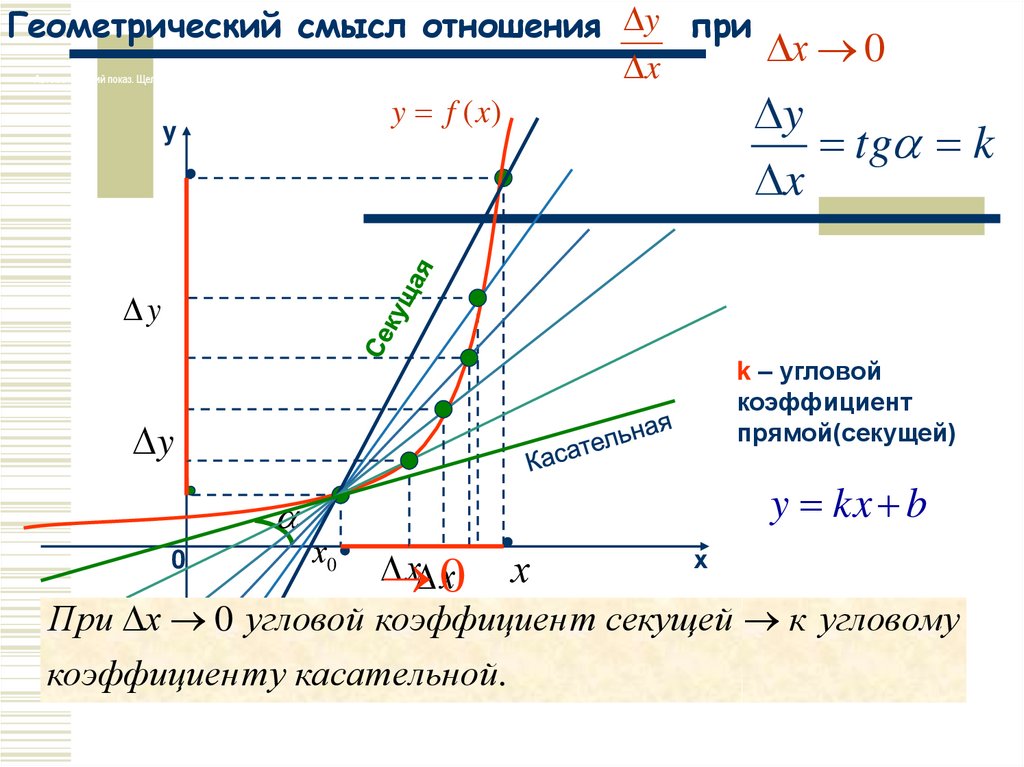
2. Геометрический смысл отношения при
Геометрический смысл отношения y прих 0
x
Автоматический показ. Щелкните 1 раз.
y f (x)
y
y
tg k
x
y
k – угловой
коэффициент
прямой(секущей)
y
y kx b
х0
х
х
х
х0
При
х стремится
0 угловой
коэффициен
секущей
угловому
Секущая
занять
положение т
касательной.
То к
есть,
касательная есть предельное положение секущей.
коэффициен
ту касательной.
0
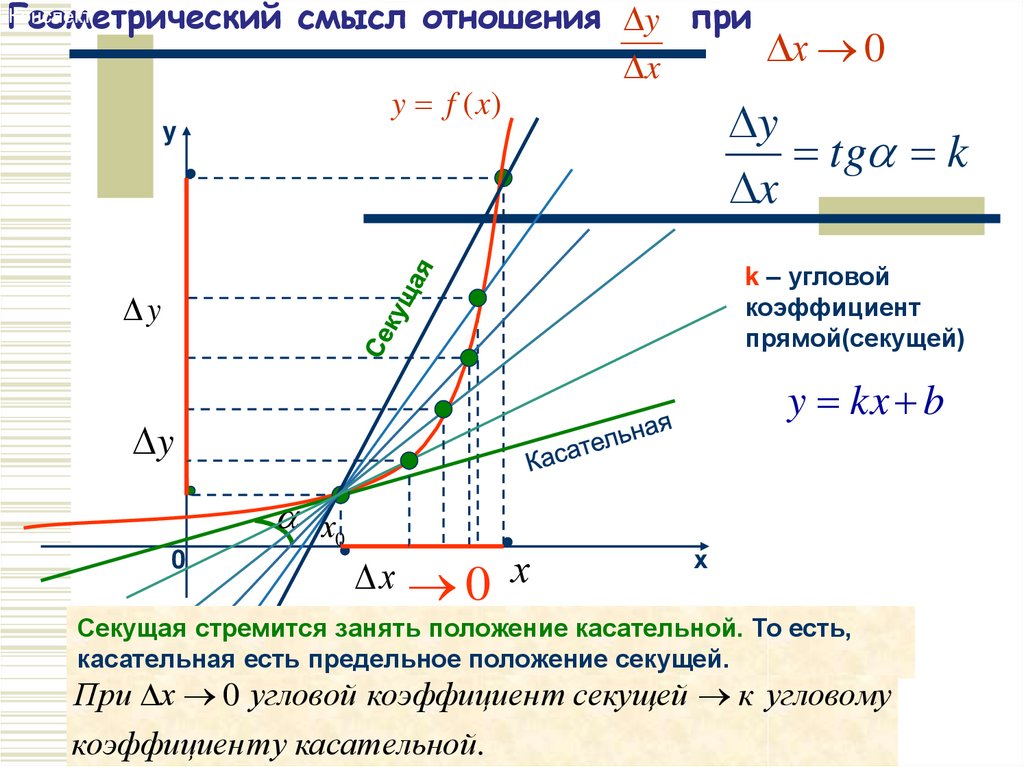
3. Геометрический смысл отношения при
Геометрический смысл отношения y прих 0
x
Конспект
y f (x)
y
tg k
x
y
k – угловой
коэффициент
прямой(секущей)
y
y kx b
y
0
х0
х 0 х
х
Секущая стремится занять положение касательной. То есть,
касательная есть предельное положение секущей.
При х 0 угловой коэффициен т секущей к угловому
коэффициен ту касательной.
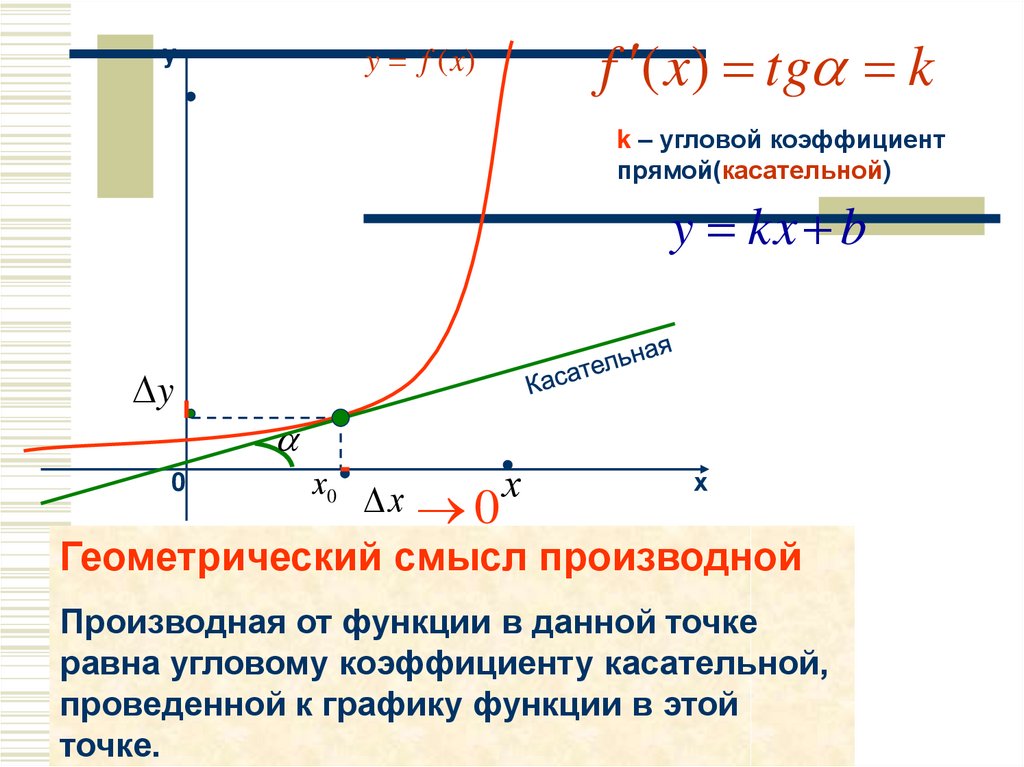
4.
f ( x) tg ky f (x)
y
k – угловой коэффициент
прямой(касательной)
y kx b
y
0
х0
х
0
х
х
Геометрический смысл производной
Производная от функции в данной точке
равна угловому коэффициенту касательной,
проведенной к графику функции в этой
точке.
5.
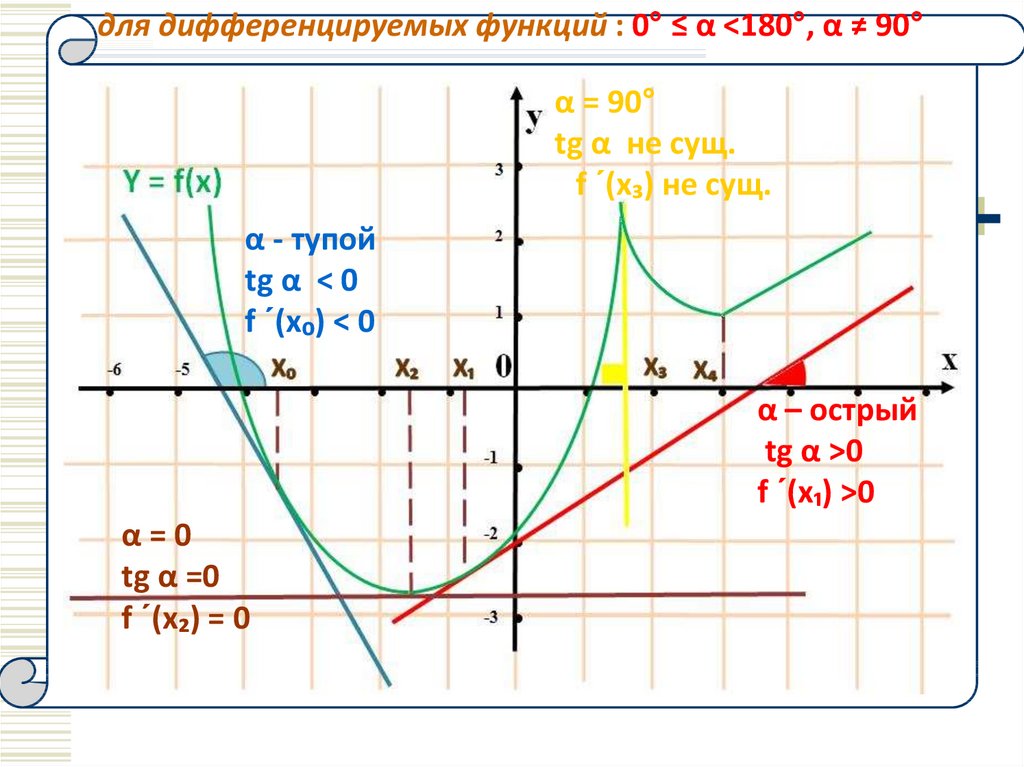
для дифференцируемых функций : 0° ≤ α ˂180°, α ≠ 90°α = 90°
tg α не сущ.
f ´(x₃) не сущ.
α - тупой
tg α < 0
f ´(x₀) < 0
α – острый
tg α >0
f ´(x₁) >0
α=0
tg α =0
f ´(x₂) = 0
6.
Физический смысл производной функциив данной точке
х
Vср.
t
Или, если х перемещение тела, а t промежуток времени ,
в течении которого выполнялось движение, то
х
средняя скорость движения на промежутке времени t.
t
При t 0 Vcр. к мгновенной скорости V (t ),
следовательно, V (t ) S (t ).
S (t ) V (t )
или х (t ) V (t )
Производная от функции в данной точке это
скорость изменения функции .
f ( х) V ( x)
.
7. Решите задачи.
1 Найдите угловой коэффициенткасательной, проведенной
к графику
3
функции у=9х-4х в его точке с абсциссой
0
х = 1.
2. Найдите тангенс угла наклона
2
y 0,5x
касательной, проведенной к графику
x0 3
функции в его точке с абсциссой .
8. 3. Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции равен 2.
h( x) 1 2 sin 2 x4. На рисунке изображен график производной .
Найдите точки минимума функции .
y f (x)
y f (x)
5. Найдите скорость и ускорение изменения функции
y x3 5 x 4
в точке .
9.
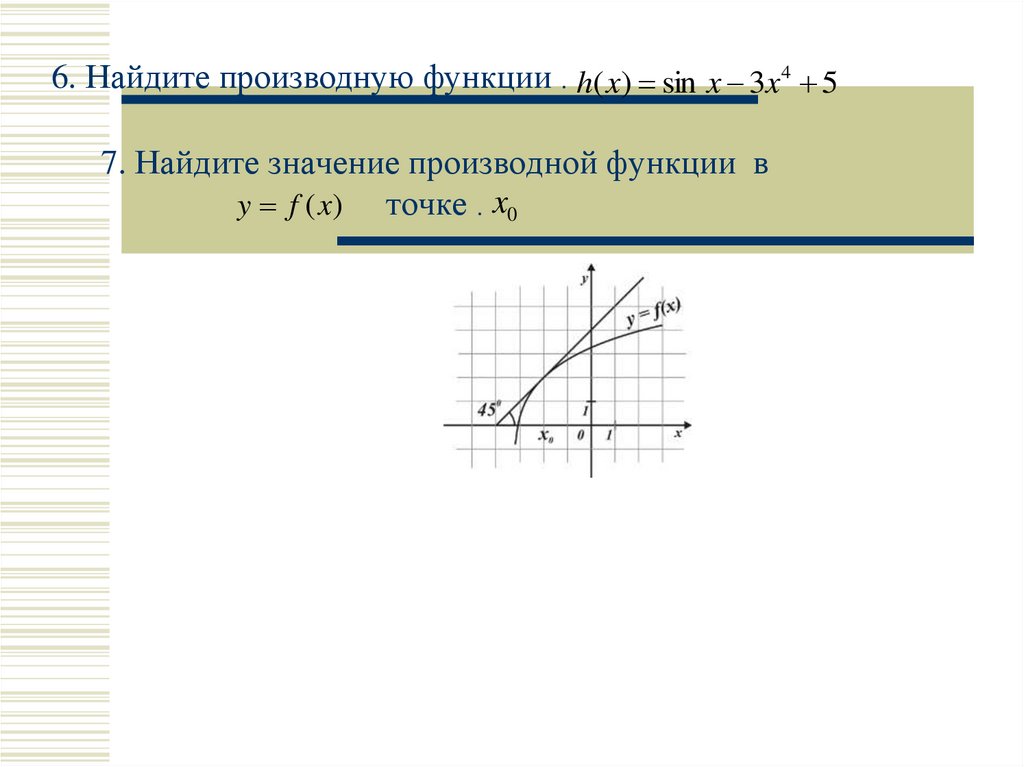
6. Найдите производную функции . h( x) sin x 3x4 57. Найдите значение производной функции в
y f (x) точке . x0
10. Домашнее задание
повторить теорию в презентации.Выполнить в тетрадях задания из
презентации
Повторить формулы вычисления
производных
На повторение: № 41.10,41.14, 42.142.3(некоторые были прорешаны ранее)





 Математика
Математика








