Похожие презентации:
Решение задач по стереометрии на ЕГЭ (многогранники)
1.
2.
3.
Задача 1.В правильной четырехугольной пирамиде
высота равна 12, объем равен 200.
Найдите боковое ребро этой пирамиды.
4.
ЗАДАЧА 2В правильной треугольной
пирамиде SABC с
вершиной S биссектрисы
треугольника ABC пересекаются
в точке O. Площадь
треугольника ABC равна 2;
объем пирамиды равен 6.
Найдите длину отрезка OS.
,
5.
ЗАДАЧА 3Найдите площадь
боковой поверхности
правильной
четырехугольной
пирамиды, сторона
основания которой равна
6 и высота равна 4.
6.
ЗАДАЧА 4Даны две правильные
четырёхугольные пирамиды.
Объём первой пирамиды равен
16. У второй пирамиды высота
в 2 раза больше, а сторона
основания в 1,5 раза больше,
чем у первой. Найдите объём
второй пирамиды.
7.
Задача 5.Основанием пирамиды служит
прямоугольник, одна боковая грань
перпендикулярна плоскости
основания, а три другие боковые
грани наклонены к плоскости
основания под углом 60°. Высота
пирамиды равна 6. Найдите объем
пирамиды.
8.
Задача 6.Объем куба равен 12. Найдите
объем четырехугольной
пирамиды, основанием которой
является грань куба, а
вершиной — центр куба.
9.
ЗАДАЧА 710.
ЗАДАЧА 811.
ЗАДАЧА 9ОСНОВАНИЕМ ПИРАМИДЫ СЛУЖИТ ПРЯМОУГОЛЬНИК, ОДНА БОКОВАЯ ГРАНЬ
ПЕРПЕНДИКУЛЯРНА ПЛОСКОСТИ ОСНОВАНИЯ, А ТРИ ДРУГИЕ БОКОВЫЕ ГРАНИ
НАКЛОНЕНЫ К ПЛОСКОСТИ ОСНОВАНИЯ ПОД УГЛОМ 60°. ВЫСОТА ПИРАМИДЫ РАВНА
6. НАЙДИТЕ ОБЪЕМ ПИРАМИДЫ.
12.
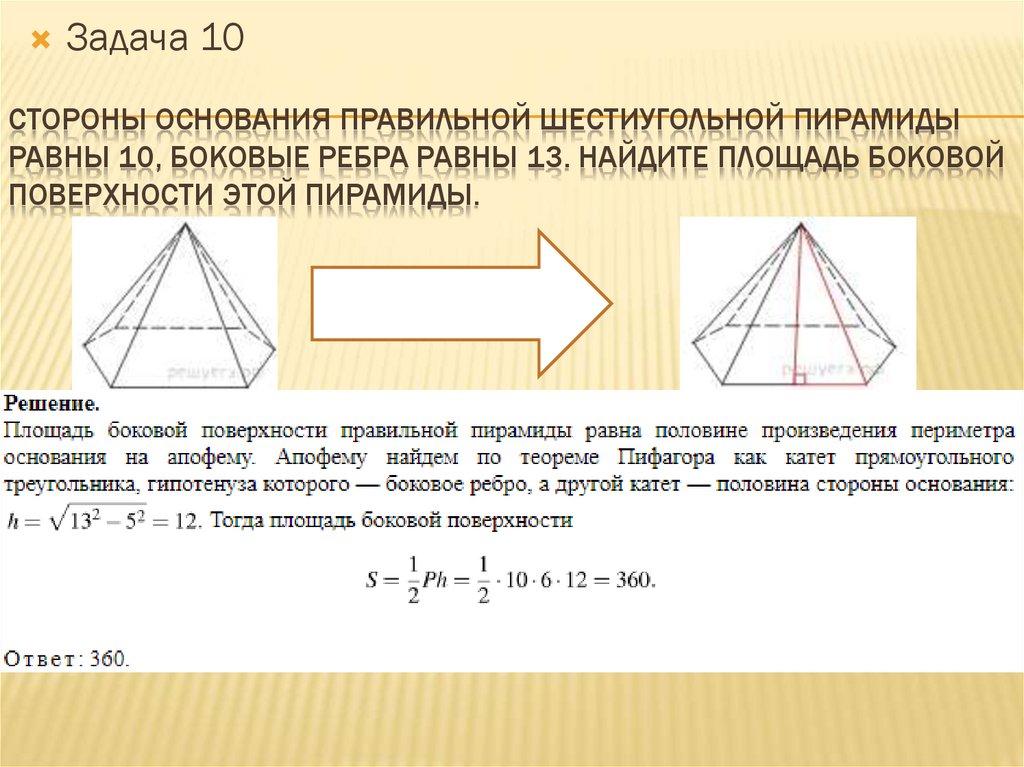
Задача 10СТОРОНЫ ОСНОВАНИЯ ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПИРАМИДЫ
РАВНЫ 10, БОКОВЫЕ РЕБРА РАВНЫ 13. НАЙДИТЕ ПЛОЩАДЬ БОКОВОЙ
ПОВЕРХНОСТИ ЭТОЙ ПИРАМИДЫ.
13.
ЗАДАЧА 11СТОРОНЫ ОСНОВАНИЯ ПРАВИЛЬНОЙ
ЧЕТЫРЕХУГОЛЬНОЙ ПИРАМИДЫ РАВНЫ
10, БОКОВЫЕ РЕБРА РАВНЫ 13.
НАЙДИТЕ ПЛОЩАДЬ ПОВЕРХНОСТИ
ЭТОЙ ПИРАМИДЫ.
14.
ЗАДАЧА 1215.
16.
ЗАДАЧА 1Площадь поверхности куба равна 18. Найдите его
диагональ.
Пояснение: Пусть ребро куба равно a, тогда площадь
поверхности куба S=6a^2, а диагональ куба d=a√3. Тогда
6a^2=18
a=√3
d=√3*√3=9
Ответ: 9
.
17.
Задача 2Объем куба равен 8. Найдите площадь его
поверхности.
Пояснение :
V=a^3
S=6a^2
8=a^3
a=2
S=6*4=24
Ответ: 24
18.
ЗАДАЧА 3Если каждое ребро куба увеличить на 1, то его площадь
поверхности увеличится на 54. Найдите ребро куба.
Пояснение: S=6a^2
Пусть a – исходная длина ребра куба.После того, как
ребро увеличили на 1, оно стало равно a+1. Площадь
поверхности куба S=6a^2
Тогда для красного куба, получим
S2=6*(a+1)^2=6a^2+12a+6
В задаче сказано, что площадь
S2=S+54=6a^2+54, имеем уравнение
6a^2+12a+6=6a^2+54
12a=48
a=4
Ответ: 4
19.
20.
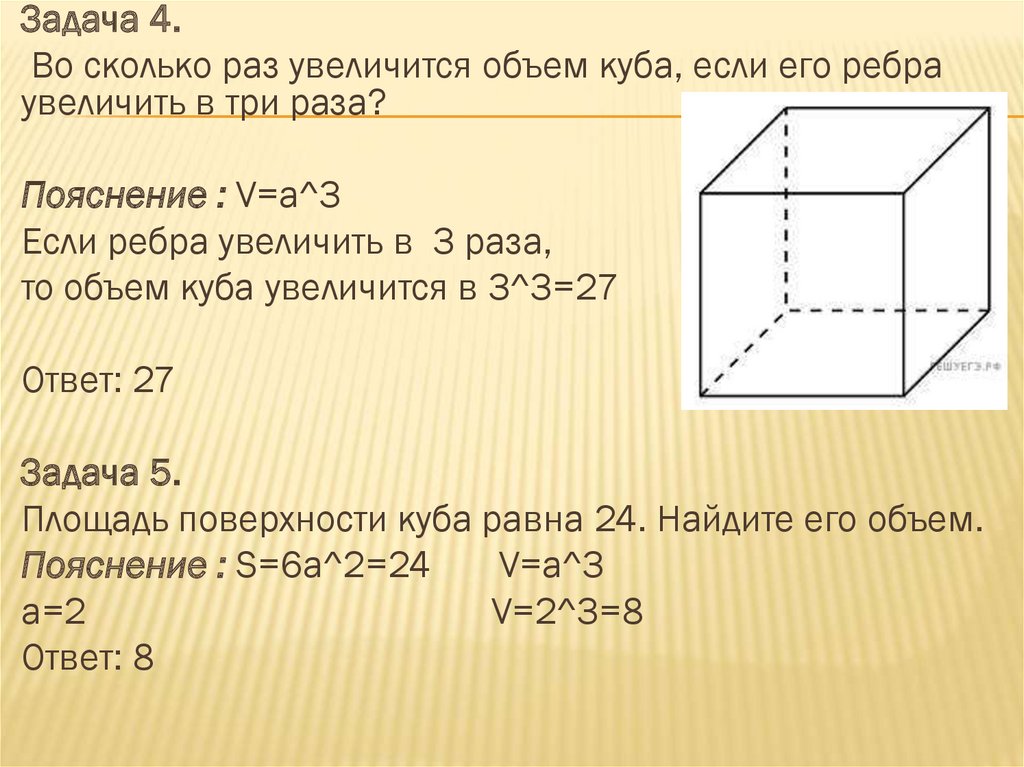
Задача 4.Во сколько раз увеличится объем куба, если его ребра
увеличить в три раза?
Пояснение : V=a^3
Если ребра увеличить в 3 раза,
то объем куба увеличится в 3^3=27
Ответ: 27
Задача 5.
Площадь поверхности куба равна 24. Найдите его объем.
Пояснение : S=6a^2=24
V=a^3
a=2
V=2^3=8
Ответ: 8
21.
Задача 6.От деревянного кубика отпилили все его вершины
(см. рисунок). Сколько граней у получившегося многогранника
(невидимые ребра на рисунке не обозначены)?
Пояснение: У кубика 6 граней.
В результате отпиливания 8 вершин
появились 8 граней. Всего 14 граней.
Ответ : 14
Задача7.
Ящик, имеющий форму куба с ребром 10 см без одной грани, нужно
покрасить со всех сторон снаружи. Найдите площадь поверхности,
которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Пояснение: Площадь одной грани равна 10 · 10 = 100 см2. В кубе шесть
граней, но нас просят найти только площадь пяти граней, следовательно
100 · 5 = 500 см2.
Ответ: 500.
22.
23.
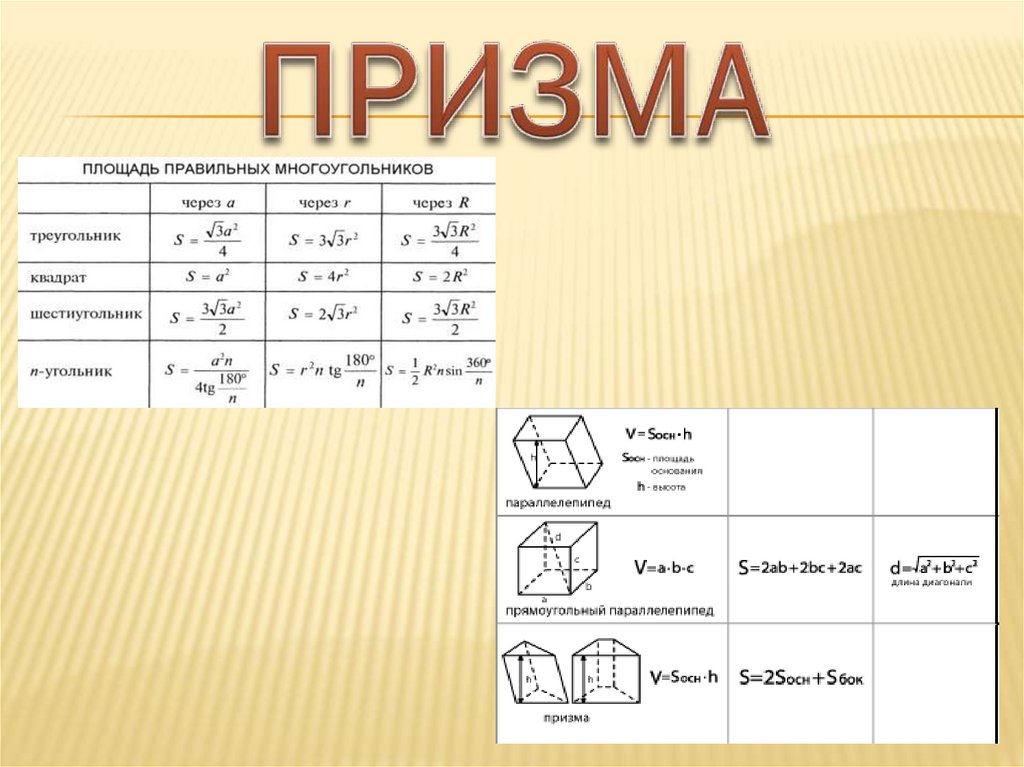
1. НАЙДИТЕ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЫ, СТОРОНА
ОСНОВАНИЯ КОТОРОЙ РАВНА 5, А ВЫСОТА – 10.
24.
2. НАЙДИТЕ ПЛОЩАДЬ ПОВЕРХНОСТИ ПРЯМОЙ ПРИЗМЫ,В ОСНОВАНИИ КОТОРОЙ ЛЕЖИТ РОМБ С ДИАГОНАЛЯМИ,
РАВНЫМИ 6 И 8, И БОКОВЫМ РЕБРОМ, РАВНЫМ 10.
25.
3. ОСНОВАНИЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫСЛУЖИТ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК С КАТЕТАМИ 6 И
8, БОКОВОЕ РЕБРО РАВНО 5. НАЙДИТЕ ОБЪЕМ ПРИЗМЫ.
26.
ЗАДАЧА 4Гранью параллелепипеда
является ромб со стороной 1 и
острым углом 60°. Одно из
ребер параллелепипеда
составляет с этой гранью угол в
60° и равно 2. Найдите объем
параллелепипеда.
27.
ЗАДАЧА 5Найдите квадрат расстояния
между
вершинами C и A1 прямоугол
ьного параллелепипеда, для
которого AB = 5, AD = 4, AA1
=3.
28.
ЗАДАЧА 6Объём куба равен 12. Найдите объём
треугольной призмы, отсекаемой от
куба плос-костью, проходящей через
середины двух рёбер, выходящих из
одной вершины, и парал-лельной
третьему ребру, выходящему из этой
же вершины.
29.
ЗАДАЧА 6ГРАНЬЮ ПАРАЛЛЕЛЕПИПЕДА ЯВЛЯЕТСЯ РОМБ СО
СТОРОНОЙ 1 И ОСТРЫМ УГЛОМ 60°. ОДНО ИЗ РЕБЕР
ПАРАЛЛЕЛЕПИПЕДА СОСТАВЛЯЕТ С ЭТОЙ ГРАНЬЮ УГОЛ В
60° И РАВНО 2. НАЙДИТЕ ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА.
30.
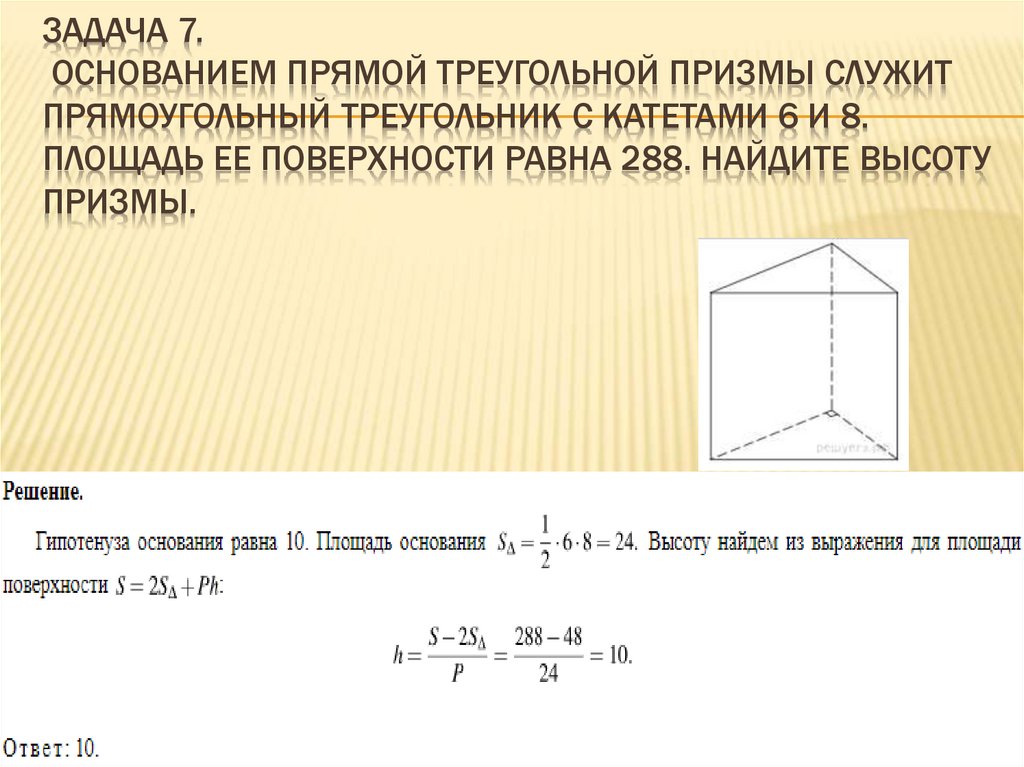
ЗАДАЧА 7.ОСНОВАНИЕМ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ СЛУЖИТ
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК С КАТЕТАМИ 6 И 8.
ПЛОЩАДЬ ЕЕ ПОВЕРХНОСТИ РАВНА 288. НАЙДИТЕ ВЫСОТУ
ПРИЗМЫ.
31.
ЗАДАЧА 8ЧЕРЕЗ СРЕДНЮЮ ЛИНИЮ ОСНОВАНИЯ ТРЕУГОЛЬНОЙ
ПРИЗМЫ ПРОВЕДЕНА ПЛОСКОСТЬ, ПАРАЛЛЕЛЬНАЯ
БОКОВОМУ РЕБРУ. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
ОТСЕЧЕННОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ РАВНА 8. НАЙДИТЕ
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ИСХОДНОЙ ПРИЗМЫ.
32.
ЗАДАЧА 9.ПЛОЩАДЬ ПОВЕРХНОСТИ ПРАВИЛЬНОЙ ТРЕУГОЛЬНОЙ
ПРИЗМЫ РАВНА 6. КАКОЙ СТАНЕТ ПЛОЩАДЬ
ПОВЕРХНОСТИ ПРИЗМЫ, ЕСЛИ ВСЕ ЕЁ РЁБРА УВЕЛИЧАТСЯ
В ТРИ РАЗА, А ФОРМА ОСТАНЕТСЯ ПРЕЖНЕЙ?
33.
ЗАДАЧА 10НАЙДИТЕ КВАДРАТ РАССТОЯНИЯ МЕЖДУ
ВЕРШИНАМИ C И A1ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА,
ДЛЯ КОТОРОГО AB = 5, AD = 4, AA1=3.
34.
ЗАДАЧА 11.В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙ ПРИЗМЕ ВСЕ РЕБРА РАВНЫ 1.
НАЙДИТЕ РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ В И Е.
35.
ЗАДАЧА 12. В ПРАВИЛЬНОЙ ШЕСТИУГОЛЬНОЙПРИЗМЕ ВСЕ РЕБРА РАВНЫ 1. НАЙДИТЕ УГОЛ DAB. ОТВЕТ
ДАЙТЕ В ГРАДУСАХ.
36.
ЗАДАЧА 13.Найдите расстояние между
вершинами А и D прямоуго
льного параллелепипеда, для
которого AB = 5, AD =
4, AA = 3.
37.
ЗАДАЧА 14.38.
ЗАДАЧА 15.39.
ЗАДАЧА 16.40.
ЗАДАЧА 17.41.
ЗАДАЧА 18.42.
ЗАДАЧА 19.43.
ЗАДАЧА 20.44.
РЕШИТЬ САМОСТОЯТЕЛЬНО, ПРОВЕРИТЬ ПОКЛЮЧУ.
1. Площадь поверхности куба равна 648. Найдите его диагональ.
2. Если каждое ребро куба увеличить на 9, то его площадь поверхности
увеличится на 594. Найдите ребро куба.
3. Во сколько раз увеличится объем куба, если его ребра увеличить в
четыре раза?
4. В правильной четырехугольной
пирамиде SABCD точка O — центр основания, S —
вершина, SO=12, SB=15. Найдите длину отрезка AC.
5. В правильной четырехугольной
пирамиде SABCD точка О – центр основания, S –
вершина, SO = 8, BD = 30
Найдите боковое ребро SC
45.
6. В правильной треугольной пирамиде SABC точка L —середина ребра AC, S — вершина. Известно,
что BC = 6, а SL = 5. Найдите площадь боковой
поверхности пирамиды.
7. В правильной треугольной пирамиде SABC L –
середина ребра AC, S– вершина. Известно, что BC=7,
а площадь боковой поверхности пирамиды равна 42.
Найдите длину отрезка SL
8. Стороны основания правильной четырехугольной пирамиды
равны 84, боковые ребра равны 58. Найдите площадь
поверхности этой пирамиды.
9. Во сколько раз увеличится площадь поверхности правильного
тетраэдра, если все его ребра увеличить в два раза?
10. Найдите площадь боковой поверхности правильной
четырехугольной пирамиды, сторона основания которой равна 6
и высота равна 4.
46.
11. Диагональ AC основания правильнойчетырёхугольной
пирамиды SABCD равна 6. Высота
пирамиды SO равна 4. Найдите длину
бокового ребра SB.
12. В правильной шестиугольной
пирамиде боковое ребро равно 17, а
сторона основания равна 8. Найдите
высоту пирамиды.









































 Математика
Математика








