Похожие презентации:
Геометрия пчелиных сот
1.
Урок геометрии 9 класс.
2.
• пчелиные соты - представляют собой прямоугольник,покрытый правильными шестиугольниками
3.
Геометрия пчелиных сот, жизнь и деятельность пчёл всегдапривлекала внимание человека.
«Странные общественные привычки и
геометрические дарования пчёл, -пишет
известный математик Герман Вейль, не могли не привлечь внимания и не
вызвать восхищения людей, наблюдавших
их жизнь и использовавших плоды их
деятельности».
4.
Задача 1.Пчелиные соты представляют собой прямоугольник,
покрытый правильными шестиугольниками ( рис).
Найти, какими ещё правильными многоугольниками
можно покрыть плоскость.
5.
Способ I (метод уравнений ).О
О
Н
А1
а)
Н
б)
рис.2
А2
А2
6.
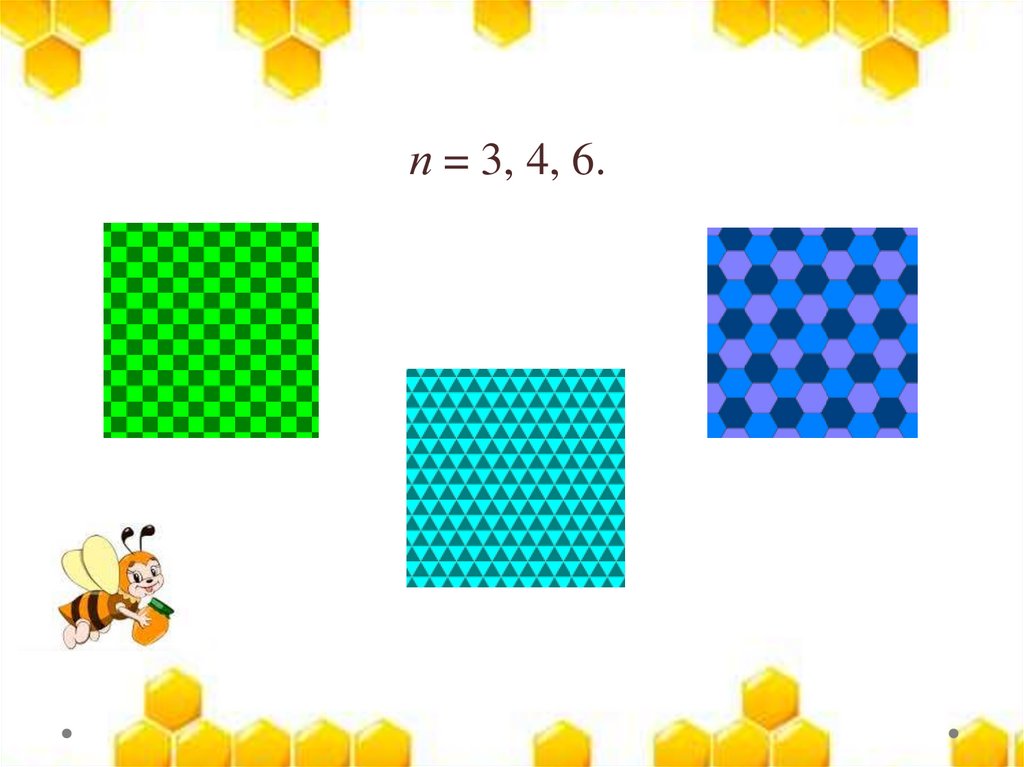
п = 3, 4, 6.7.
Способ II ( метод перебора).n= 3 Три угла, плотно
составленные, составляют
1800, шесть углов – 3600,
плоскость покрыта без
просветов
n= 3
n = 4 Четыре угла вместе
дают 3600, т. е. 900 4 = 3600,
плоскость покрыта без
просветов
n=4
8.
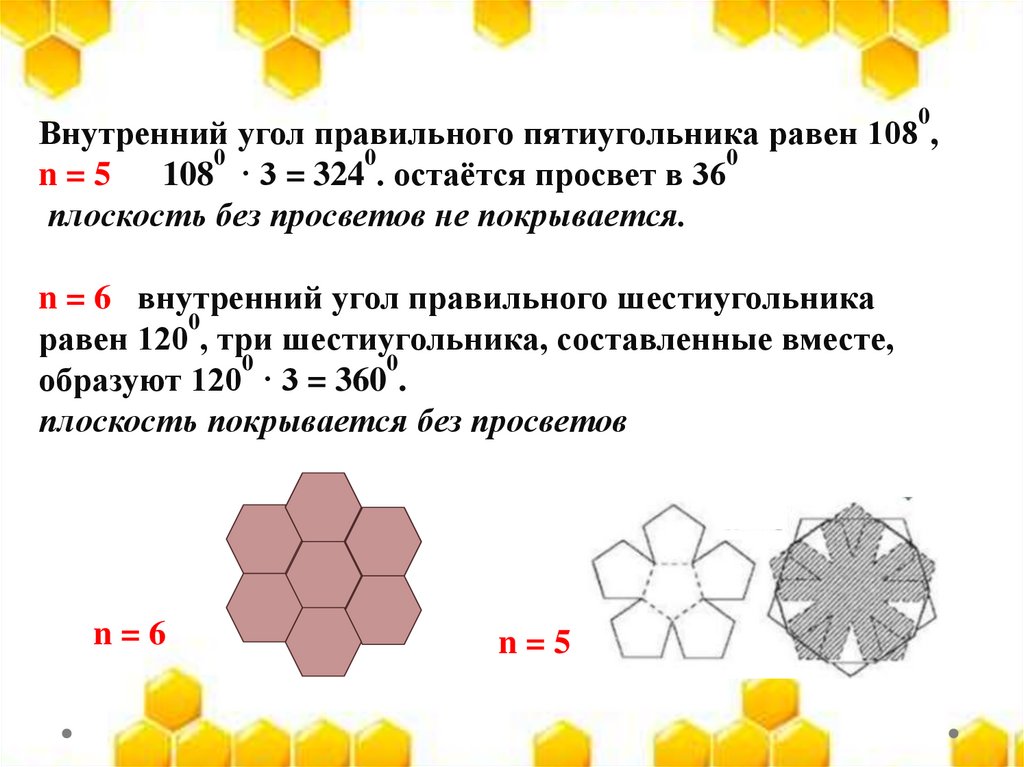
0Внутренний угол правильного пятиугольника равен 108 ,
0
0
0
n = 5 108 · 3 = 324 . остаётся просвет в 36
плоскость без просветов не покрывается.
n = 6 внутренний угол правильного шестиугольника
0
равен 120 , три шестиугольника, составленные вместе,
0
0
образуют 120 · 3 = 360 .
плоскость покрывается без просветов
n=6
n=5
9.
Почему пчёлы выбрали именношестиугольник?
Задание: сравнить периметры разных многоугольников,
имеющих одинаковую площадь
Вывод: наименьший периметр при одинаковой площади
у шестиугольника!
10.
Практическая работаПерелетая от цветка к цветку, эти
насекомые опыляют растения,
одновременно собирая цветочный
нектар и перенося его в соты.
Масса одной пчелиной ноши
нектара около 6 мг.
Чтобы накопить в улье 50 г мёда,
пчела должна сделать примерно
8333 вылета.
А для получения 100 г мёда пчела
должна облететь почти миллион
цветков, зато при хорошей
«лётной» погоде за лето можно
получить до 25 кг мёда.
11.
Домашнее задание• Можно ли без просветов в перекрытий покрыть
плоскость правильными многоугольниками, если
этими многоугольниками являются:
а) шестиугольник, квадрат и треугольник;
б) восьмиугольник и квадрат;
в) двенадцати угольник и треугольник?
Почему? (привести примеры, где используется)
• (по желанию) Соберите рецепты народной медицины.
В которых использованы продукты, даваемые
пчёлами.










 Математика
Математика








