Похожие презентации:
Свойства функций. Определение функции
1.
Тема урока:Свойства функций
2.
Определение функцииЕсли для каждого элемента x из
некоторого множества Х по некоторому
правилу f поставлен в соответствие
один и только один элемент y из
множества Y, то говорят, что задана
функция y=f(x)
3.
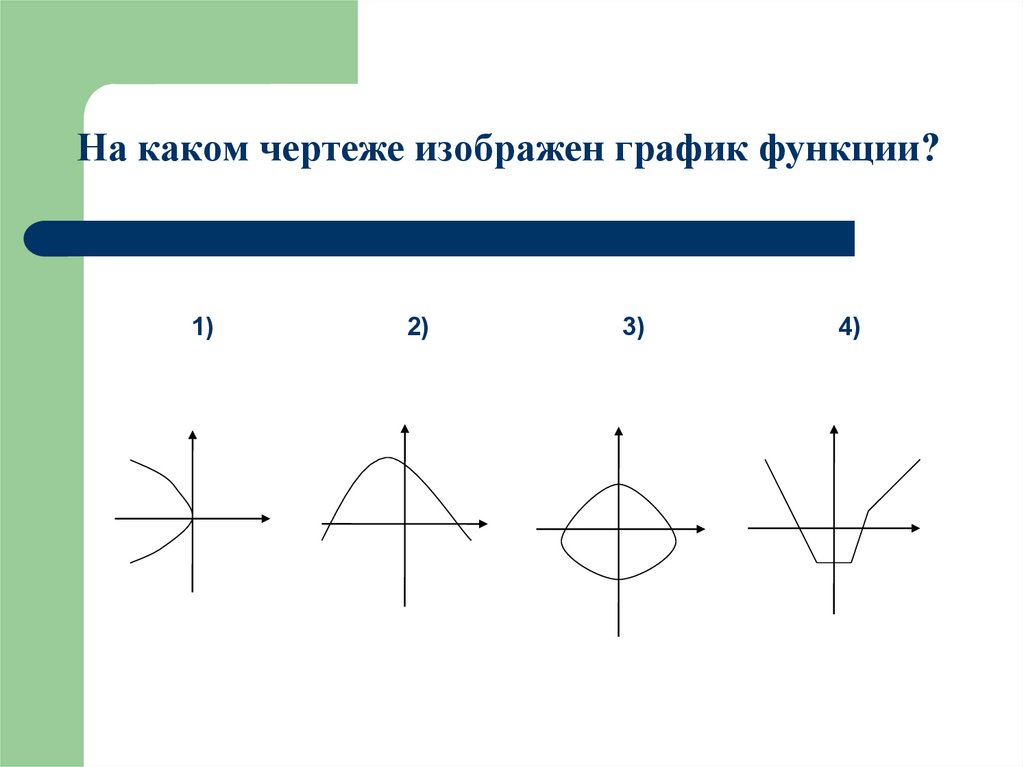
На каком чертеже изображен график функции?1)
2)
3)
4)
4.
Способы задания функции1. Формула
2. Графический
3. Табличный
5.
Задана функцияy(x) = 2x-3
1. Определите
y(0),
y(3),
y(-0,5).
2. Определите
значение
аргумента, если
значение функции
равно 7 и 0.
6.
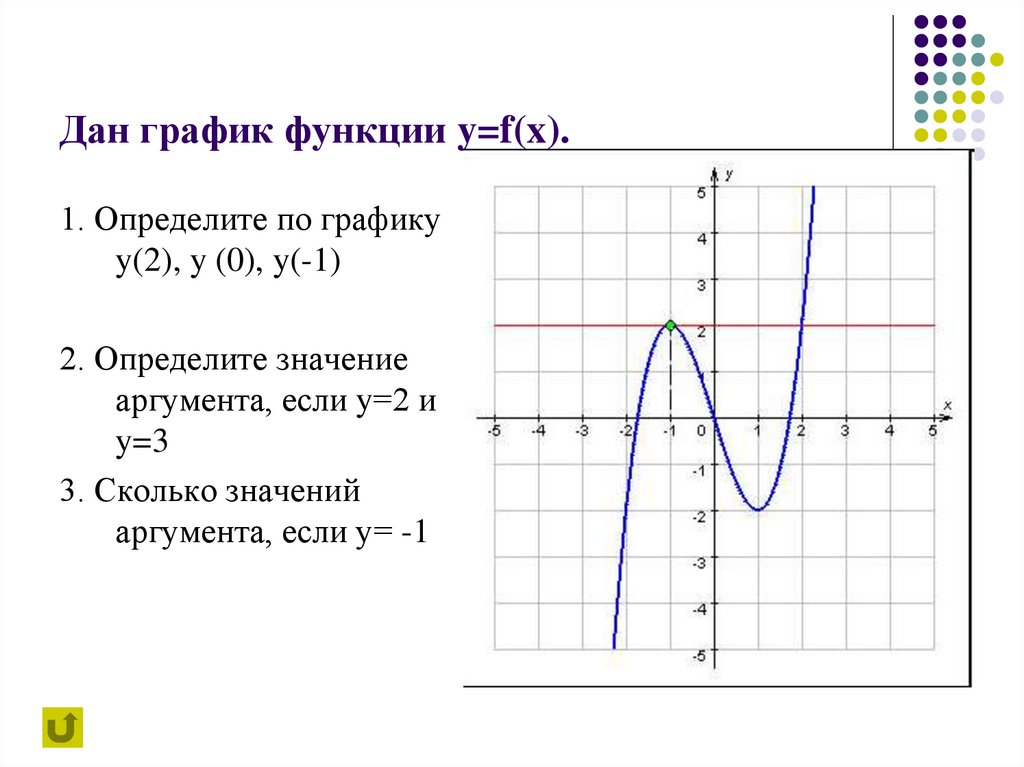
Дан график функции y=f(x).1. Определите по графику
y(2), y (0), y(-1)
2. Определите значение
аргумента, если y=2 и
y=3
3. Сколько значений
аргумента, если у= -1
7.
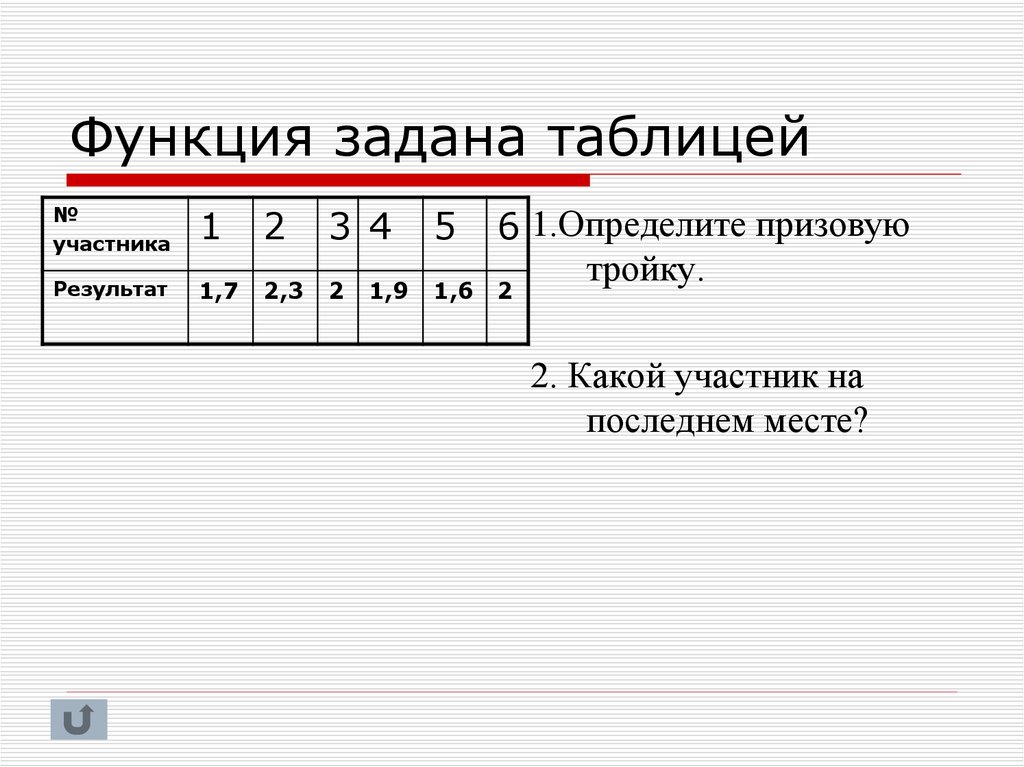
Функция задана таблицей№
участника
1
2
3 4
5
Результат
1,7
2,3
2
1,6
1,9
6 1.Определите призовую
тройку.
2
2. Какой участник на
последнем месте?
8.
Возрастание и убывание функцииФункция возрастает на
некотором
промежутке, если
большему значению
аргумента
соответствует большее
значение функции.
Функция убывает на
некотором
промежутке, если
большему значению
аргумента
соответствует
меньшее значение
функции.
9.
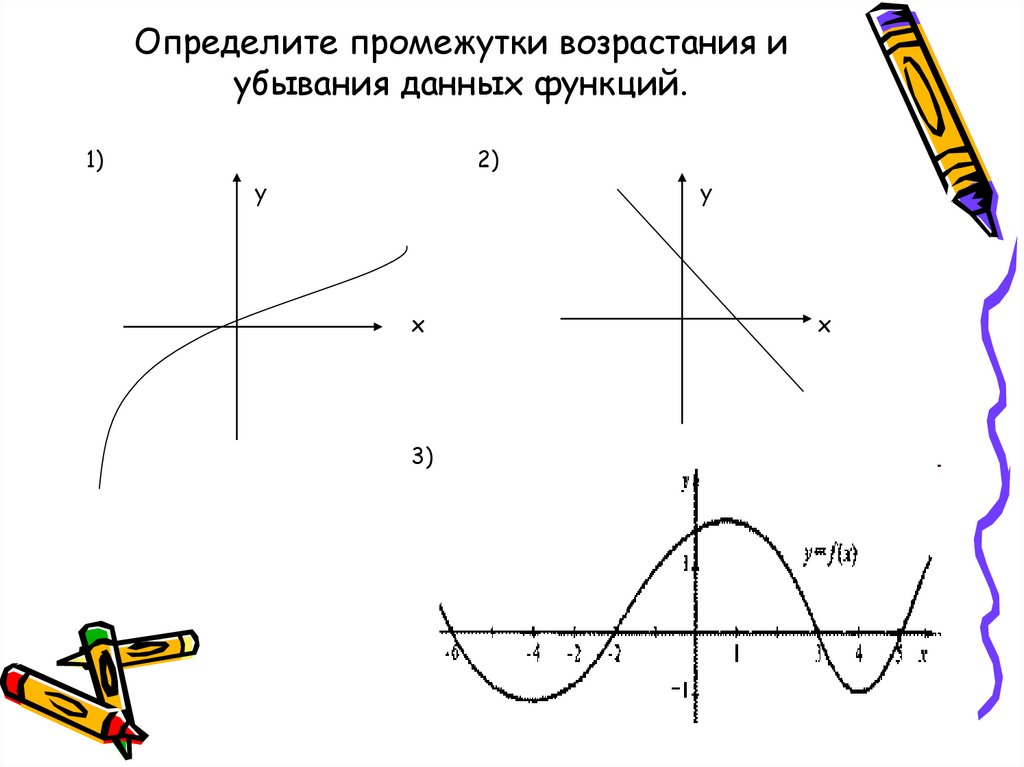
Определите промежутки возрастания иубывания данных функций.
1)
2)
y
y
x
3)
x
10.
Четные и нечетные функцииФункция y=f(x)
называется четной,
если для любого
допустимого х
выполняется равенство
Функция y=f(x)
называется нечетной,
если для любого
допустимого х
выполняется равенство
f(-x)=f(x)
f(-x)= - f(x)
11.
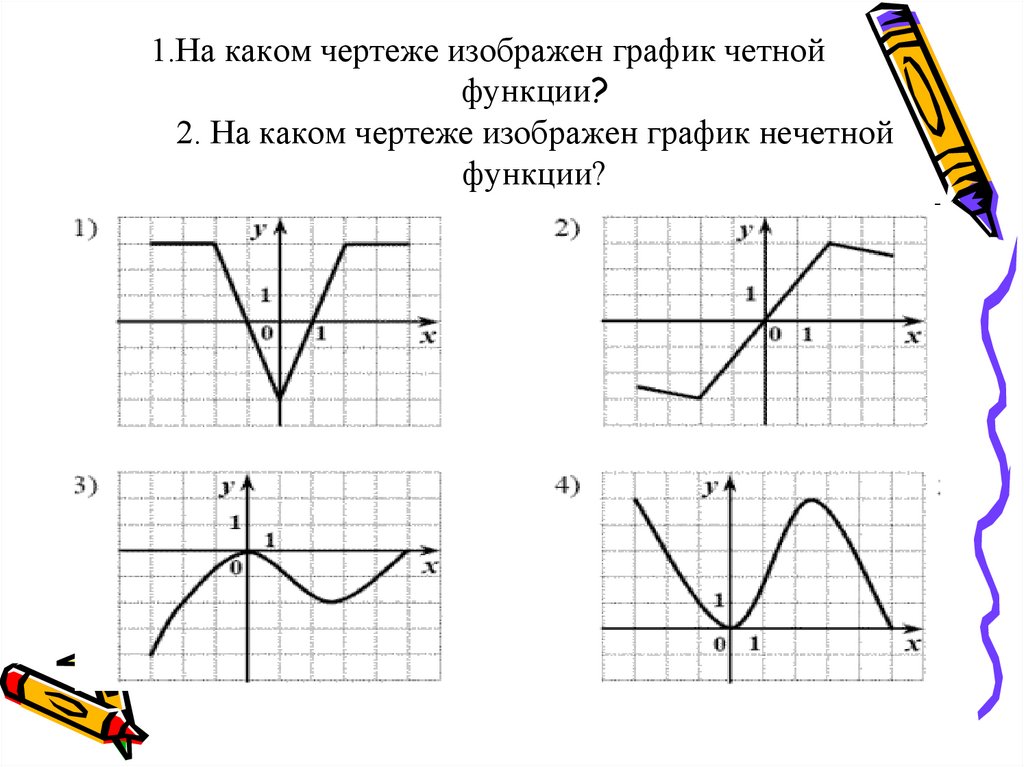
1.На каком чертеже изображен график четнойфункции?
2. На каком чертеже изображен график нечетной
функции?
12.
Определите (четная или нечетная) даннаяфункция?
1.
2.
3.
4.
y=5x2 + 6
y= 9-x3
y=|x|+4x4
y=3x-8x2
13.
Область определения функцииМножество значений аргумента.
Ограничения области определения возможны
в следующих случаях:
1)
Если функция содержит дробь с
аргументом в знаменателе;
2)
Если функция содержит корень четной
степени с аргументом в подкоренном
выражении.
14.
Найдите область определения функции:1)
y 4 x
2) y=x2 - 3x + 5
3)
1
f x
x 5
4)
y 3 x
5)
1 25 x
y
3
15.
А теперь переходим к тесту…УДАЧИ!










 Математика
Математика