Похожие презентации:
Виды квадратных уравнений
1.
Урок алгебры в 8 классеУчитель МБОУ СОШ №30
Будрица Е. Г.
2.
3.
Тест. Виды квадратных уравнений.2. 6х2 + 9 = 0
3. х2 – 3х = 0
4. х2 - 9х +20 = 0
5. 2х2 - 9х + 10 =0
6. 3х2=0
7. 2х2+5х-7=0
8. 3х2+7х+4=0
неполное
полное
1. 3х2 - 14х +16 = 0
приведенное
неприведенное
4.
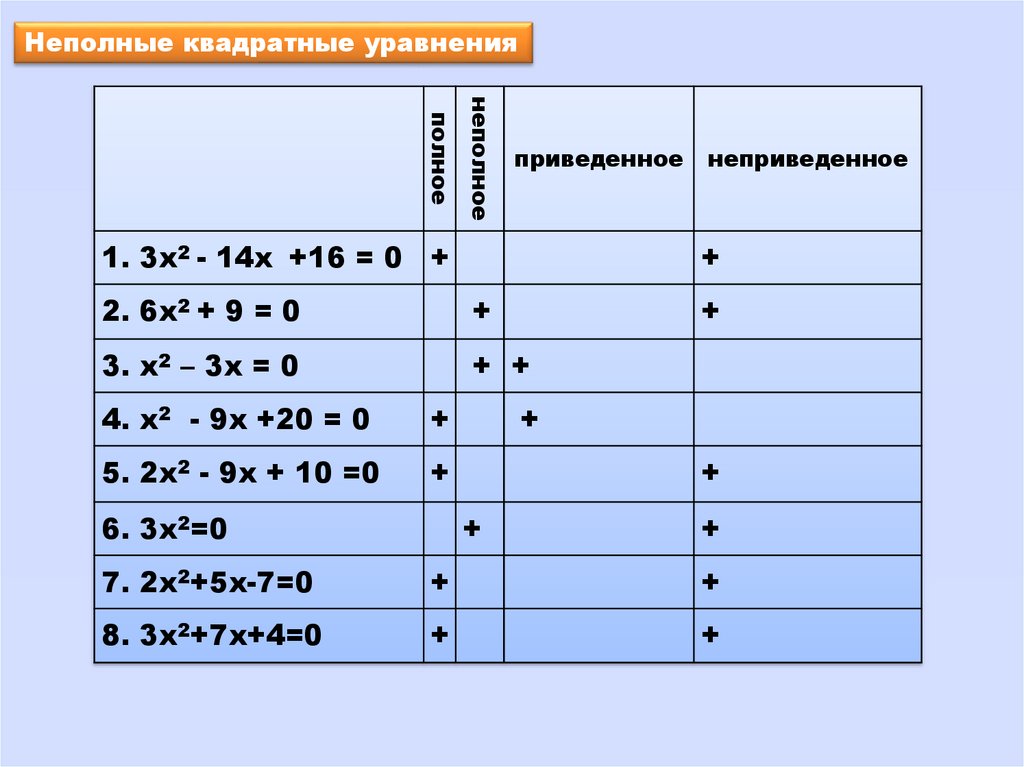
Неполные квадратные уравнениянеполное
полное
приведенное
1. 3х2 - 14х +16 = 0 +
+
2. 6х2 + 9 = 0
+
3. х2 – 3х = 0
+ +
4. х2 - 9х +20 = 0
+
5. 2х2 - 9х + 10 =0
+
6. 3х2=0
неприведенное
+
+
+
+
+
7. 2х2+5х-7=0
+
+
8. 3х2+7х+4=0
+
+
5.
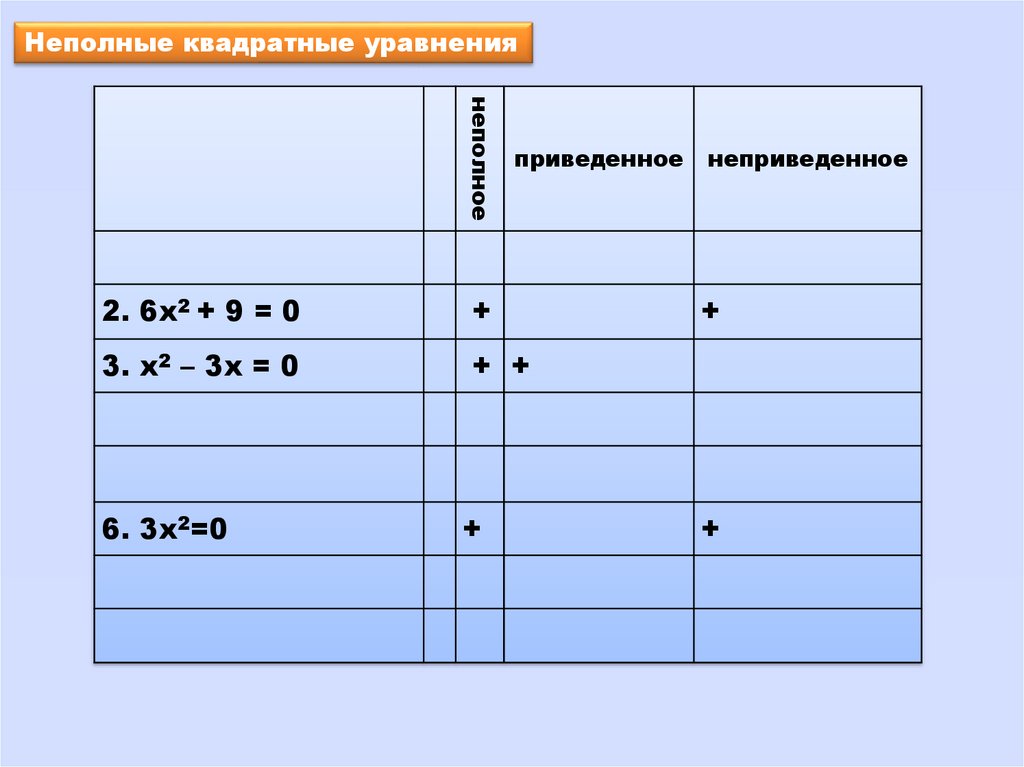
Неполные квадратные уравнениянеполное
приведенное
2. 6х2 + 9 = 0
+
3. х2 – 3х = 0
+ +
6. 3х2=0
+
неприведенное
+
+
6.
Посредством уравнений, теоремОн уйму всяких разрешал проблем.
И засуху предсказывал, и ливни –
Поистине его познанья дивны.
Древнегреческий ученый, живший в III веке,
которого по праву называют «отцом
алгебры»
А. 1 – 5х2=0;
Д. х2 - 7 = 0;
И. х2 + 2х =0;
Н. х2 – 4х + 4 = 0;
О. 5х2 = 0;
Т. х – 4=0;
Ф. х2+5 = 0.
7.
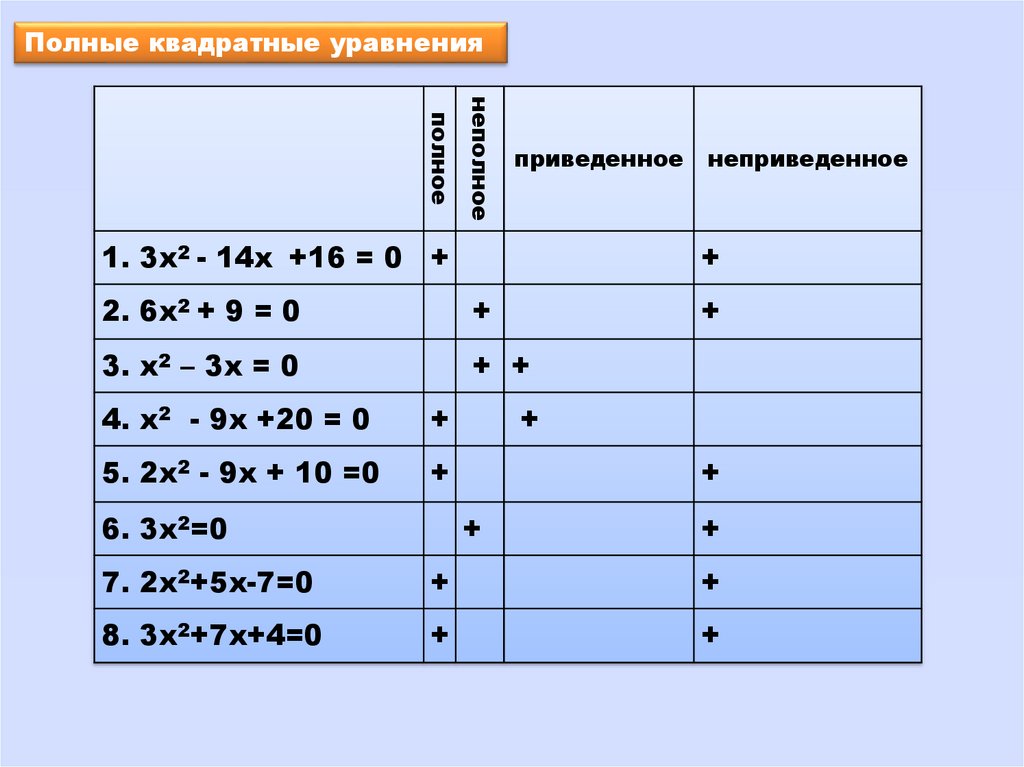
Полные квадратные уравнениянеполное
полное
приведенное
1. 3х2 - 14х +16 = 0 +
+
2. 6х2 + 9 = 0
+
3. х2 – 3х = 0
+ +
4. х2 - 9х +20 = 0
+
5. 2х2 - 9х + 10 =0
+
6. 3х2=0
неприведенное
+
+
+
+
+
7. 2х2+5х-7=0
+
+
8. 3х2+7х+4=0
+
+
8.
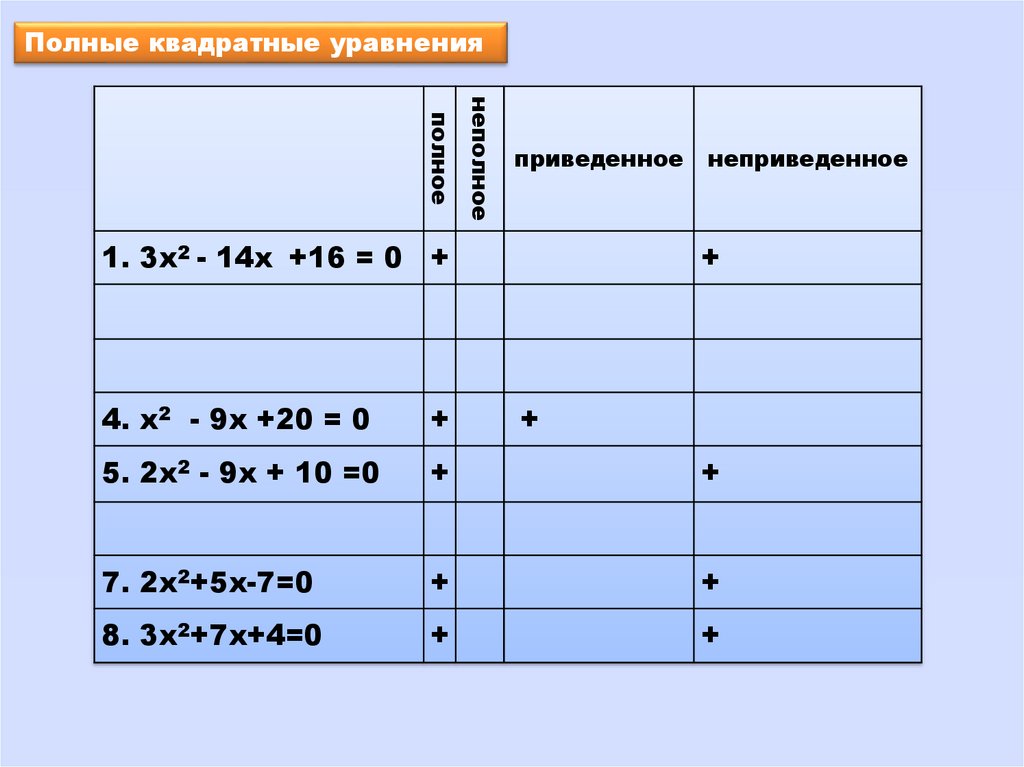
Полные квадратные уравнениянеполное
полное
приведенное
1. 3х2 - 14х +16 = 0 +
неприведенное
+
4. х2 - 9х +20 = 0
+
+
5. 2х2 - 9х + 10 =0
+
+
7. 2х2+5х-7=0
+
+
8. 3х2+7х+4=0
+
+
9.
Соедините линиями способы решения квадратных уравненийнаиболее подходящие соответствующему уравнению
1)Используя основную
формулу корней квадратного
уравнения.
2)С помощью формулы корней
квадратного уравнения с
четным вторым
коэффициентом
3)С помощью т. Виета
(подбором)
4)Используя свойства
коэффициентов квадратного
уравнения
1)3х2 - 14х +16 = 0
2) 2х2+5х-7=0
3) х2 - 9х +20 = 0
4) 2х2 - 9х + 10 =0
5) 3х2+7х+4=0
10.
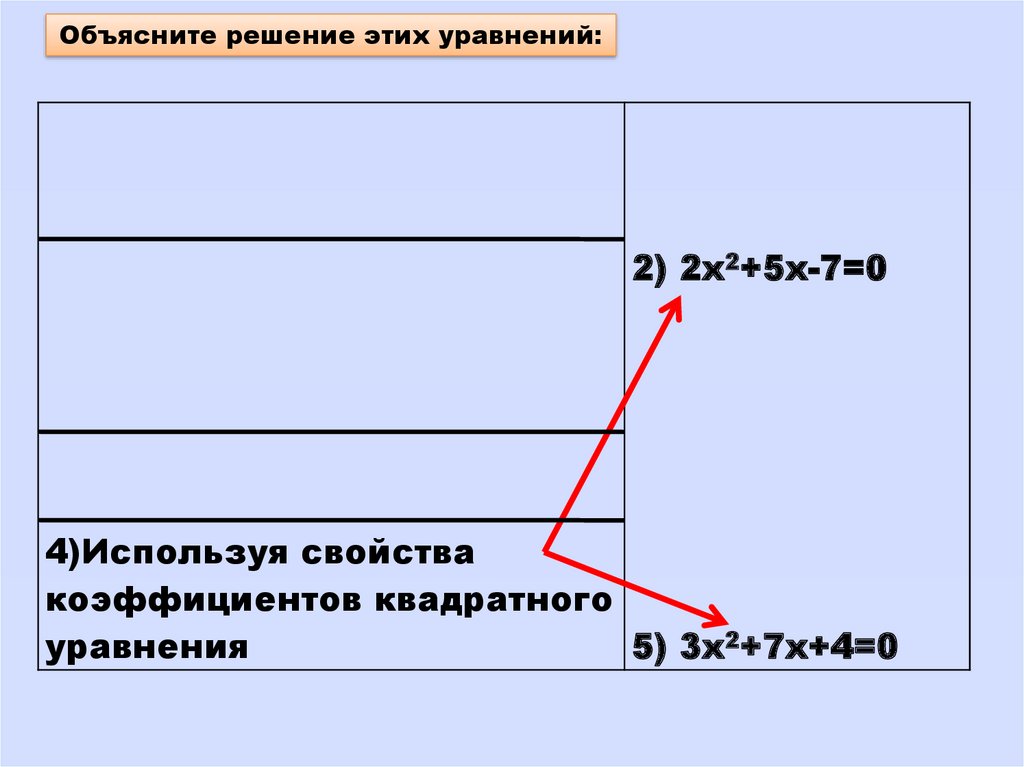
Объясните решение этих уравнений:2) 2х2+5х-7=0
4)Используя свойства
коэффициентов квадратного
уравнения
5) 3х2+7х+4=0
11.
Решив уравнения, расшифруйте слово:1. 101х2 – 103х +2 = 0
1;
2. 67 х2 + 70х +3 = 0
-1;
3. 2013х2 - х - 2012 = 0
1;
4. 1999х2 + 2000х +1 = 0
5.
23х2
+ 43х +20 = 0
6. 89х2 – 49х - 40 = 0
-
3
67
-
-1;
2012
2013
2
101
1;
-1;
40
89
-
1
1999
20
23
12.
КОРЕНЬОпределив дискриминанта знак,
Количество корней узнает всяк.
Коль знак этот плюс, то излишни слова.
У уравненья корней ровно……..
На уравнение я посмотрю,
Дискриминант его равен нулю.
Тебе я поведаю, мой господин,
Что в случае этом корень…….
Коль минус с тобою мы замечаем,
То это обрадует даже лентяя.
Тогда уравненье корней………..
И прекращается сразу решенье.
13.
Самостоятельная работаВариант – 1
Вариант – 2
1. Найдите t:
1. Найдите t:
а) 2х2 + tх – 10 =0, если
уравнение имеет корень 5;
а) 3х2 + tх +24 =0, если
уравнение имеет корень 3;
б) (t – 1) x2 – (t +1) x=72, если б) (t – 5) x2 – (t - 2) x + 6t=0, если
уравнение имеет корень 3.
уравнение имеет корень 2.
2. При каких значениях t
2. При каких значениях t
уравнение х2 + tх+9=0 имеет уравнение 4х2 + tх+1=0 имеет
один корень?
один корень?
14.
t = 2 t =6 иt=-6
t=14
t= -17 t= - 8 t =4 и
t=-4










 Математика
Математика








