Похожие презентации:
Золотое сечение
1.
ЗОЛОТОЕ СЕЧЕНИЕМатематика на каждом шагу.
Автор: учитель математики
ФГБОУ ВО Предуниверситарий МГЛУ г. Москва
Шингарева Светлана Алексеевна
2.
Математика и искусство.У школьников часто складывается
впечатление, что математика занимается
только числами и измерениями. На самом
деле, математика- это нечто гораздо
большее, чем просто наука для счетоводов и
кассиров. Математика и искусство: сегодня
2 великие сферы культуры, тесно
переплетающиеся крепкими незримыми
узами.
3.
«Золотое сечение» в искусстве.Вопрос о роли математики в искусстве волновал еще древних
греков. Иоганн Кеплер говорил, что геометрия владеет двумя
сокровищами- теоремой Пифагора и золотым сечением и если
первое можно сравнить с мерой золота, то второе- с
драгоценным камнем.
«Золотым сечением» и даже «божественной пропорцией»
называли математики древности деление отрезка, при
котором длина всего отрезка так относится к длине большей
части, как длина большей части к меньшей. Это отношение
приближенно равно 0,618 или 5/8. Цифры, выражающие
длины отрезков, оставляют ряд Фибоначчи. Ряд чисел:
0,1,1,2,3,5,8,13,21,34,55 и тд. Особенность- каждое число,
начиная с третьего, равен сумме двух предыдущих: 0+1=1,
1+1=2,1+2=3,2+3=5,3+5=8 и тд. , а отношение смежных чисел
равно отношению «золотого деления».
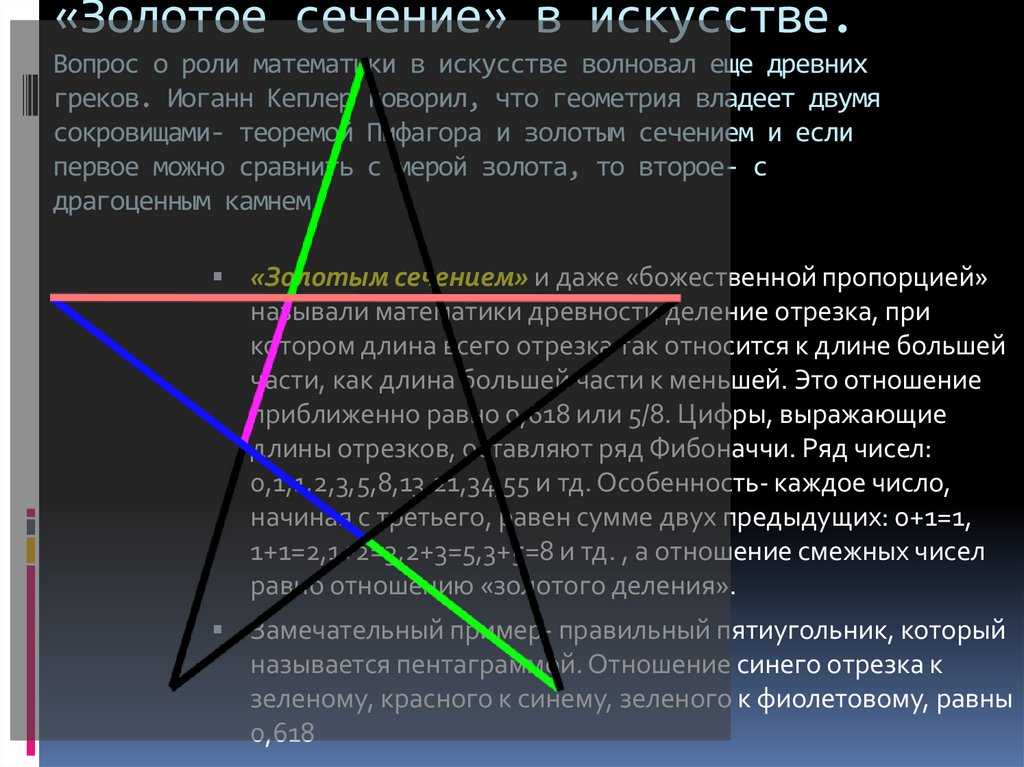
Замечательный пример- правильный пятиугольник, который
называется пентаграммой. Отношение синего отрезка к
зеленому, красного к синему, зеленого к фиолетовому, равны
0,618
4.
Математика и музыка.Необходимую, существенную связь музыки и
числа обнаружили еще пифагорейцы,
которые, открыв числовые соотношения,
лежащие в основе музыкальных созвучий, и
являлись родоначальниками музыкальной
теории.
Причем, чем талантливее композитор, тем в
большем количестве его произведений
найдено «золотых сечений». У Бетховена,
Бородина, Гайдна, Моцарта, Скрябина,
Шопена и Шуберта «золотые сечения»
найдены в 90% всех произведений.
5.
Математика и поэзия.Что роднит их, казалось, на первый
взгляд они такие разные…
Софья Васильевна Ковалевская- великий
математик, признанный писатель и поэт
говорит о математике так: «Это наука,
требующая наиболее фантазии, нельзя
быть математиком, не будучи в то же
время поэтом в душе.»
Александр Сергеевич Пушкинвеликий русский поэт, драматург и
писатель, в стихотворениях
которого также проявляются
элементы «золотого сечения»..
Произведенный анализ его
стихотворений показал, что их
размеры распределены весьма
неравномерно; оказалось, что
Пушкин явно предпочитает размеры
в 5,8,13,21 и 34 строк. (числа
Фибоначчи!)
6.
«Золотое сечение» в живописи.Человек различает окружающие его предметы по форме. Форма,
в основе построения которой лежат сочетание симметрии и
«золотого сечения», способствует наилучшему зрительному
восприятию и появлению ощущения красоты и гармонии.
Рассмотрим «Золотое сечение» в
картине И.И.Шишкина «Сосновая роща».
Ярко освещенная солнцем сосна(на 1
плане) делит картину по золотому
сечению. Справа пригорок делит правую
часть картины по горизонтали, слева –
множество сосен.
«Золотая спираль» в картине
Рафаэля «Избиение младенцев».
На подготовительном эскизе
проведены линии, идущие от цент
вдоль фигур ребенка, женщины,
война. Если их соединить, то
получается золотая спирать.
«Золотое сечение» в картине
Леонардо да Винчи «Джоконда».
Композиция рисунка построена на
«золотых треугольниках»,
являющихся кусками пентаграммы
7.
«Золотое сечение» у человека.Деление тела точкой пупаважнейший показатель золотого
сечения. Пропорции мужского
тела- 13:8=1,625 , женского8:51,6 , новорожденного- 1:1.
Пропорции сечения
проявляются и в отношении
длины плеча, предплечья, кисти,
пальцев; лица.
Великий древнегреческий
скульптор использовал «золотое
сечение» в своих
произведениях. Зевс
Олимпийский ( чудо света) и
Афина Парфенос, создающая
впечатление гармонии красоты.
8.
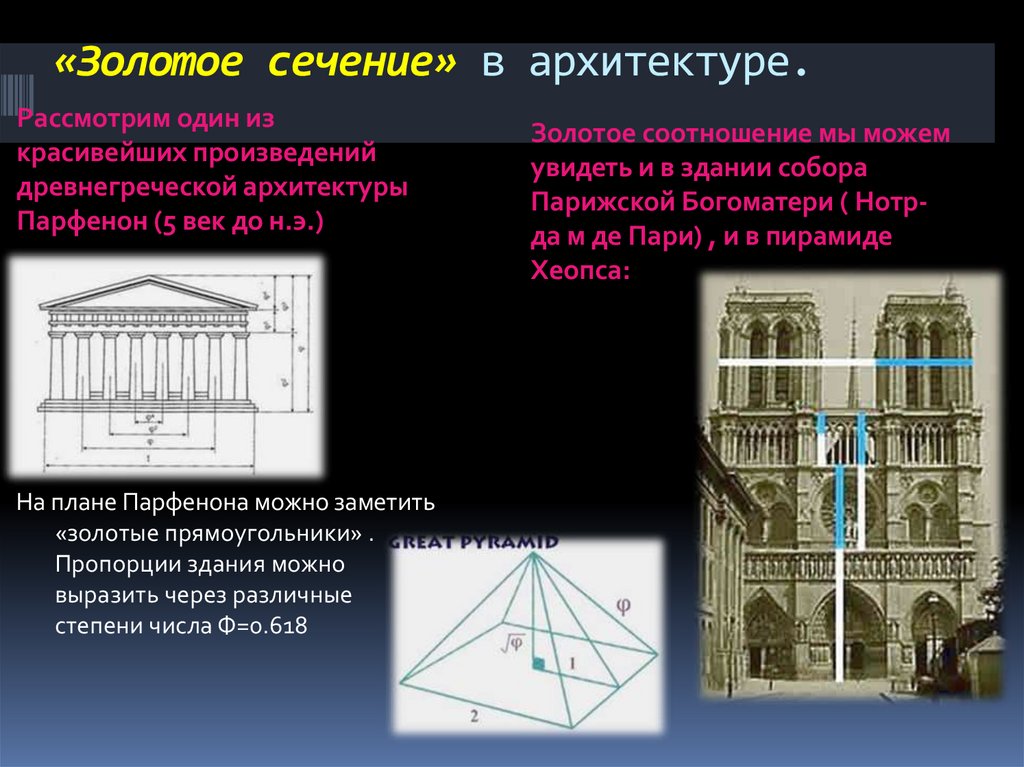
«Золотое сечение» в архитектуре.Рассмотрим один из
красивейших произведений
древнегреческой архитектуры
Парфенон (5 век до н.э.)
На плане Парфенона можно заметить
«золотые прямоугольники» .
Пропорции здания можно
выразить через различные
степени числа Ф=0.618
Золотое соотношение мы можем
увидеть и в здании собора
Парижской Богоматери ( Нотрда м де Пари) , и в пирамиде
Хеопса:
9.
«Золотое сечение» и симметрия в природе.Можно ли «проверить алгеброй гармонию»? «Да»,-считал
Леонардо и указал, как это сделать. «Золотое сечение»- не
середина, а пропорция- несложно математическое соотношение,
содержащее в себе «закон звезды и формулу цветка».
В биологических исследованиях было
показано, что, начиная с вирусов и
растений и кончая организмом
человека, всюду выявляется золотая
пропорция- универсальный закон.
Паук плетет паутину
спиралеобразно, спиралью
закручивается ураган. Спираль
увидели в расположении семян
подсолнечника, алое, капусты
брокколи, идеальный примерстебли и цветы тысячелистника,
расположенные по правилу (числу)
Фибоначчи.
10.
По примерам попробуем рассмотреть один из самыхудивительных и красивых архитектурных сооружений
России- храм Василия Блаженного в Москве.
Рассмотрим чертеж Покровского
собора:
-если взять высоту храма за единицу,
то основные пропорции, определяющие
членение целого на части, образуют
ряд «золотого сечения»;
-увидим, что таких делений в храме
семь;
-высота всего сооружения так
относится к высоте большей части,
как высота большей к меньшей;
-при вычислении получим отношение
равное 0,618
СЛЕДОВАТЕЛЬНО собор построен по
принципу «золотого сечения».
11.
Заключение.Математика окружает нас еще с древних времен. Уже
в Древней Греции родилось представление о том, что
основа прекрасного есть гармония, что стало
важнейшей категорией познания, целью, ибо в
конечном итоге художник ищет истину в красоте, а
ученый- красоту в истине.









 Математика
Математика








