Вычислительная математика. Лекция 2

1.

ВЫЧИСЛИТЕЛЬНАЯ
МАТЕМАТИКА
Лекция 2

2.

Лекцию читает
к.т.н.,доцент
БОБРОВА
ЛЮДМИЛА ВЛАДИМИРОВНА
[email protected]

3.

Тематика курса
Интерполяция
функций
Приближенное
решение
уравнений
и систем
Приближенное
интегрирование
Численное
интегрирование
дифференциальных
уравнений

4.

3. Приближенное решение
нелинейных уравнений

5.

Далеко не каждое уравнение может быть решено
точно.
Уравнения, не имеющие методов точных
решений, бывают:
Алгебраическими (x5-x3+6x-2=0);
Тригонометрическими (4sin2x+5cos2,5x-2=0);
Показательными (23x+5+8x-3-1=0);
Иррациональными (
x
x 1
2
3x
x 1
2
0
);
Трансцендентными (12sin3x+xlnx-7=0).

6.

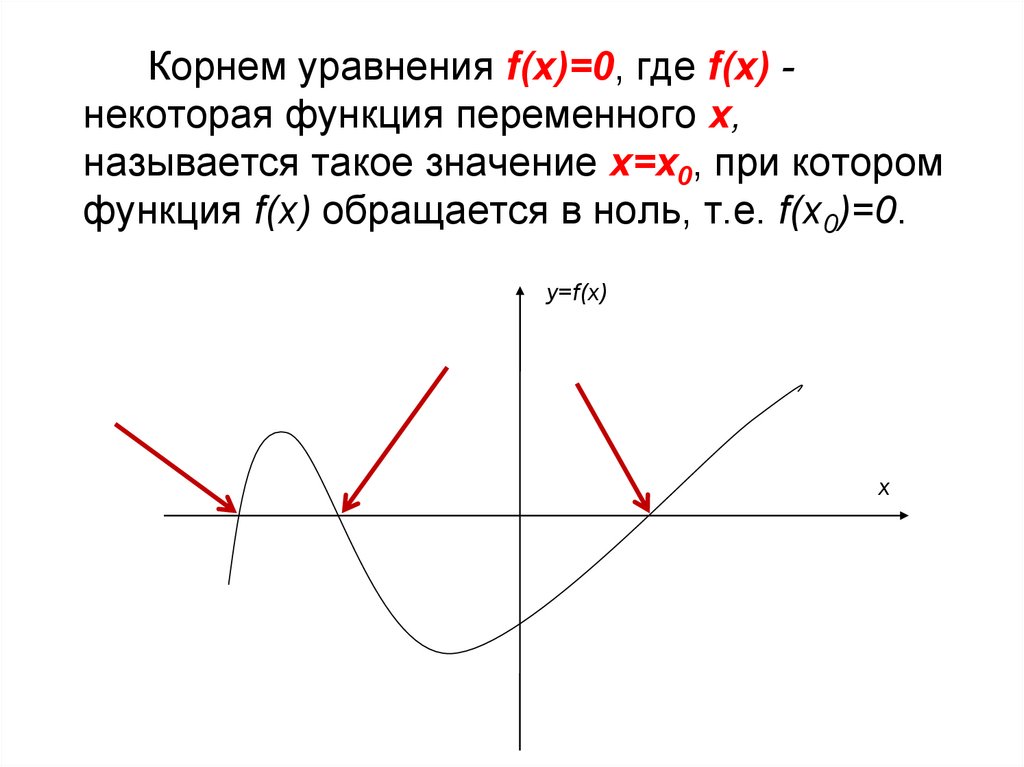
Корнем уравнения f(x)=0, где f(x) некоторая функция переменного x,
называется такое значение x=x0, при котором
функция f(x) обращается в ноль, т.е. f(x0)=0.
y=f(x)
x

7.

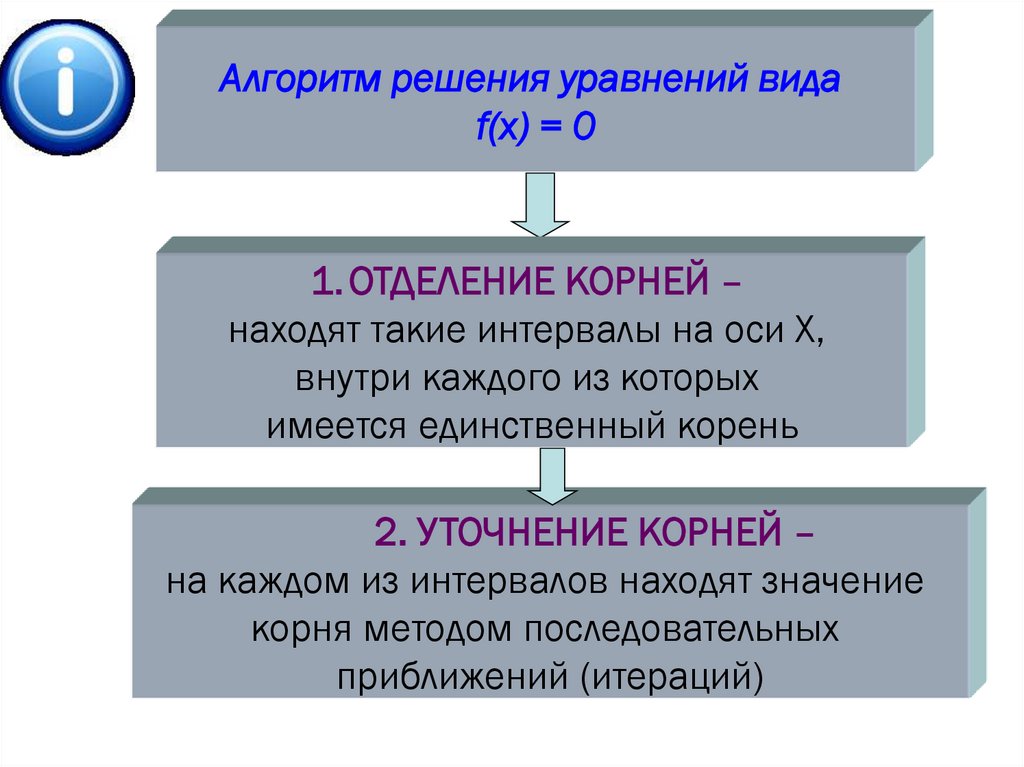
Алгоритм решения уравнений вида
f(x) = 0
1. ОТДЕЛЕНИЕ КОРНЕЙ –
находят такие интервалы на оси Х,
внутри каждого из которых
имеется единственный корень
2. УТОЧНЕНИЕ КОРНЕЙ –
на каждом из интервалов находят значение
корня методом последовательных
приближений (итераций)

8.

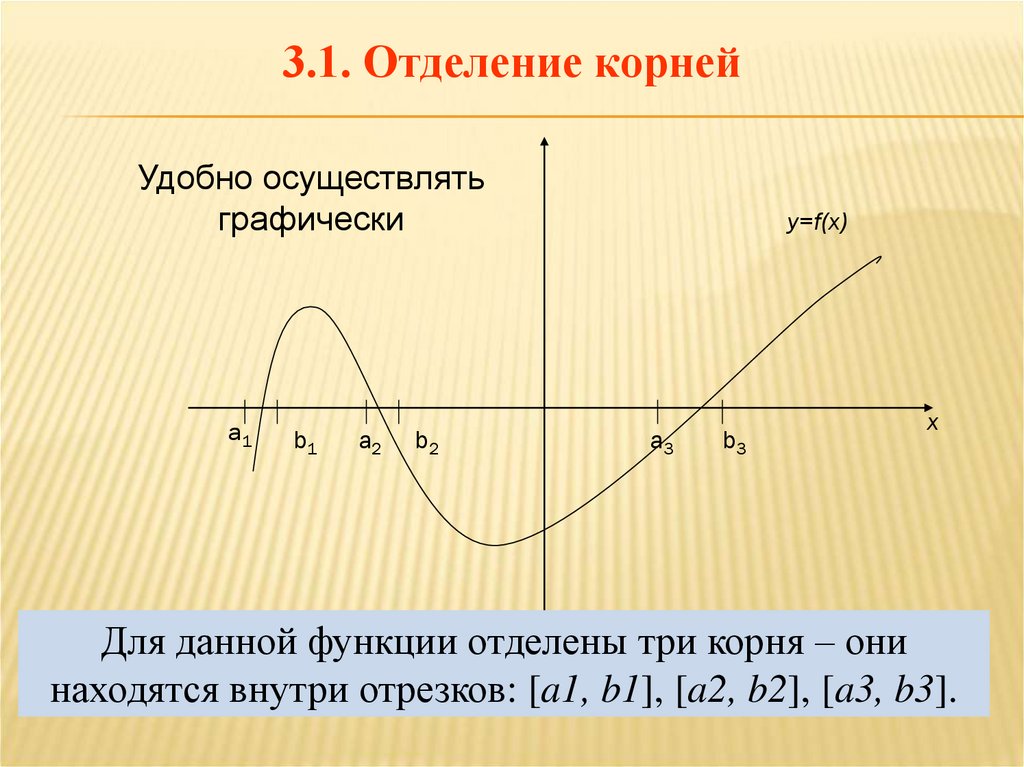
3.1. Отделение корней
Удобно осуществлять
графически
a1
b1
a2
b2
y=f(x)
a3
b3
x
Для данной функции отделены три корня – они
находятся внутри отрезков: [a1, b1], [a2, b2], [a3, b3].

9.

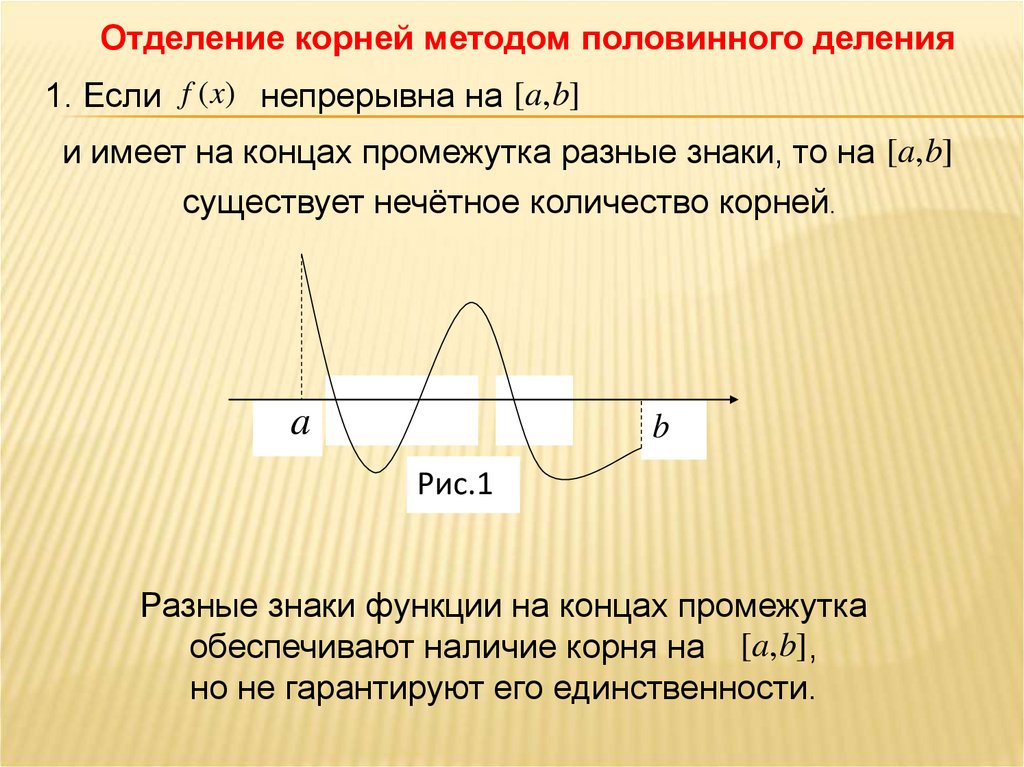
Отделение корней методом половинного деления
1. Если f ( x) непрерывна на [a, b]
и имеет на концах промежутка разные знаки, то на [a, b]
существует нечётное количество корней.
a
b
Рис.1
Разные знаки функции на концах промежутка
обеспечивают наличие корня на [a, b] ,
но не гарантируют его единственности.

10.

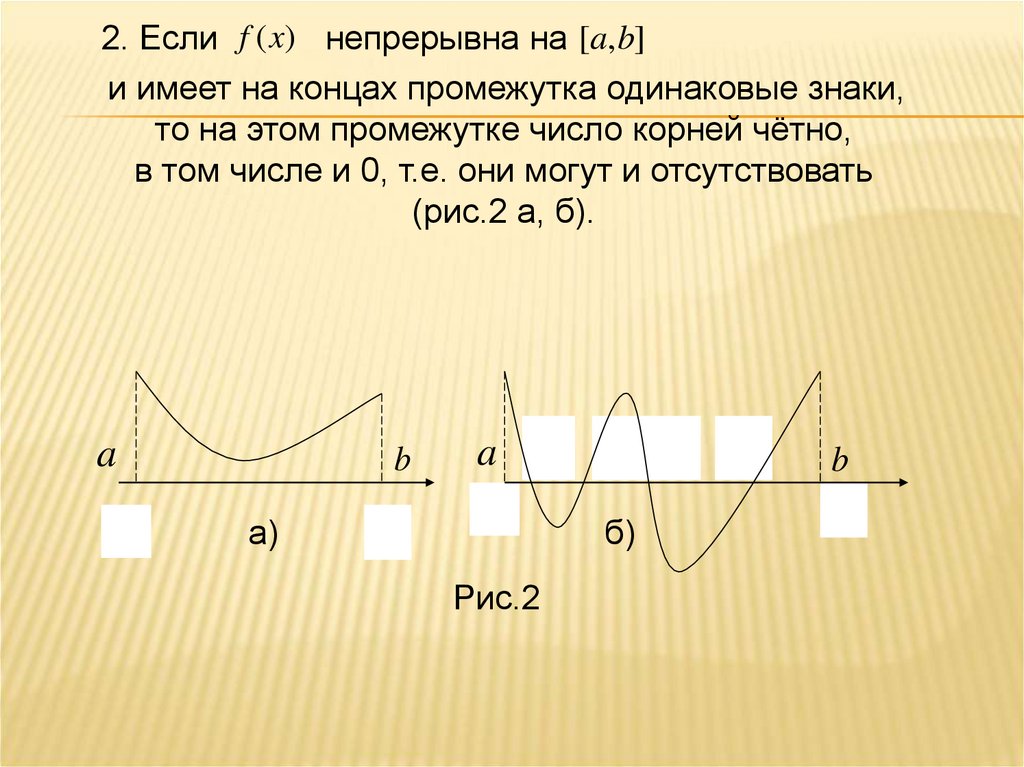
2. Если f ( x) непрерывна на [a, b]
и имеет на концах промежутка одинаковые знаки,
то на этом промежутке число корней чётно,
в том числе и 0, т.е. они могут и отсутствовать
(рис.2 а, б).
a
b
a
а)
b
б)
Рис.2

11.

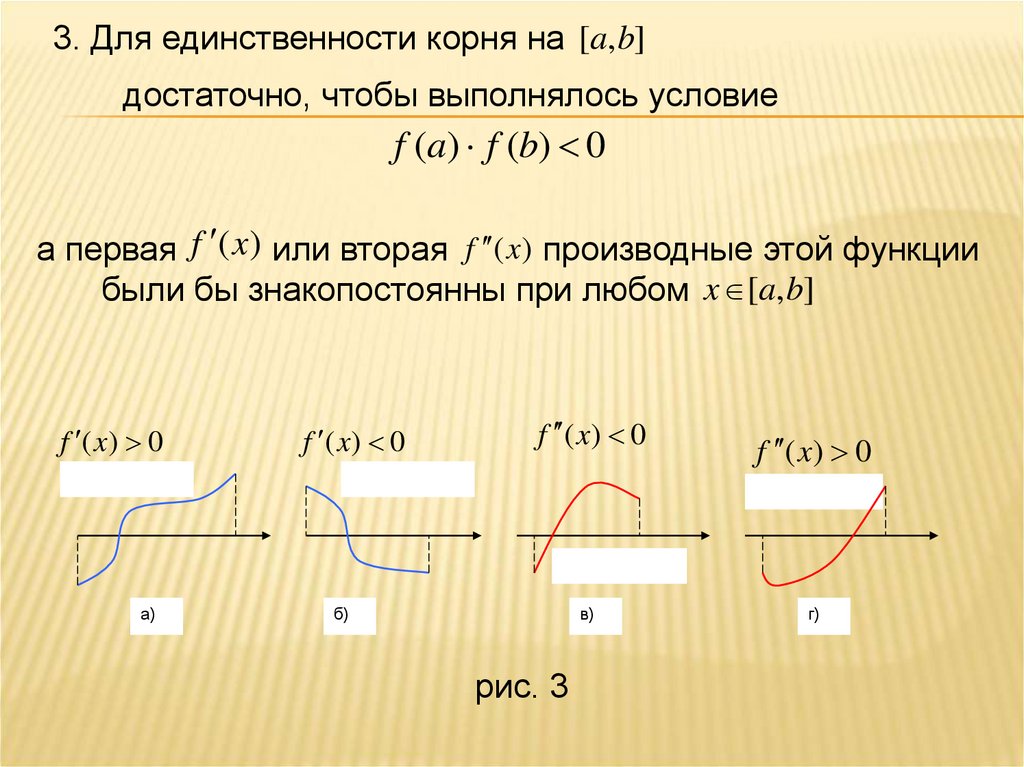
3. Для единственности корня на [a, b]
достаточно, чтобы выполнялось условие
f (a) f (b) 0
а первая f ( x ) или вторая f ( x ) производные этой функции
были бы знакопостоянны при любом x [a, b]
f ( x) 0
а)
f ( x) 0
f ( x) 0
б)
в)
рис. 3
f ( x) 0
г)

12.

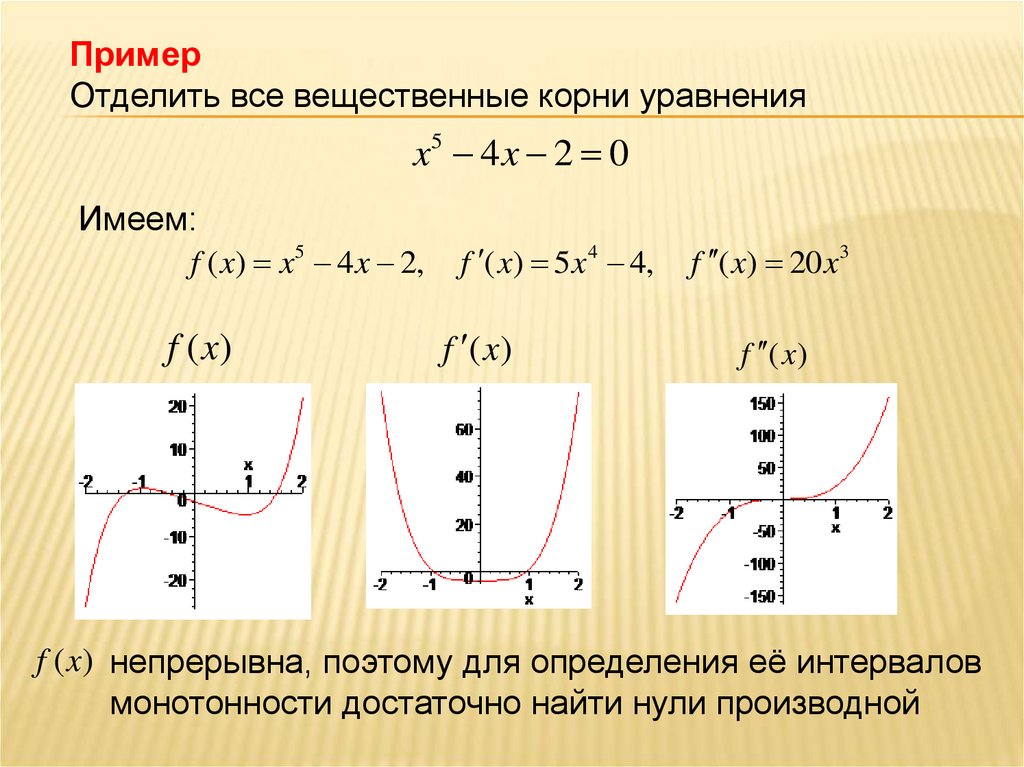
Пример
Отделить все вещественные корни уравнения
x5 4 x 2 0
Имеем:
f ( x) x5 4 x 2,
f ( x)
f ( x) 5 x 4 4,
f ( x )
f ( x) 20 x3
f ( x )
f ( x) непрерывна, поэтому для определения её интервалов
монотонности достаточно найти нули производной

13.

При этом f ( 4 0.8) 1.026373149,
f ( 4 0.8) -5.026373149,
4
4
(
0.8;
0.8) ( 0.946; 0.946)
следовательно, на промежутке
есть единственный корень.
Чтобы отделить два оставшихся корня, вычислим
f ( 1) 1 0
Тогда на промежутке ( 1; 4 0.8)
f (a) f (b) 0 корня нет

14.

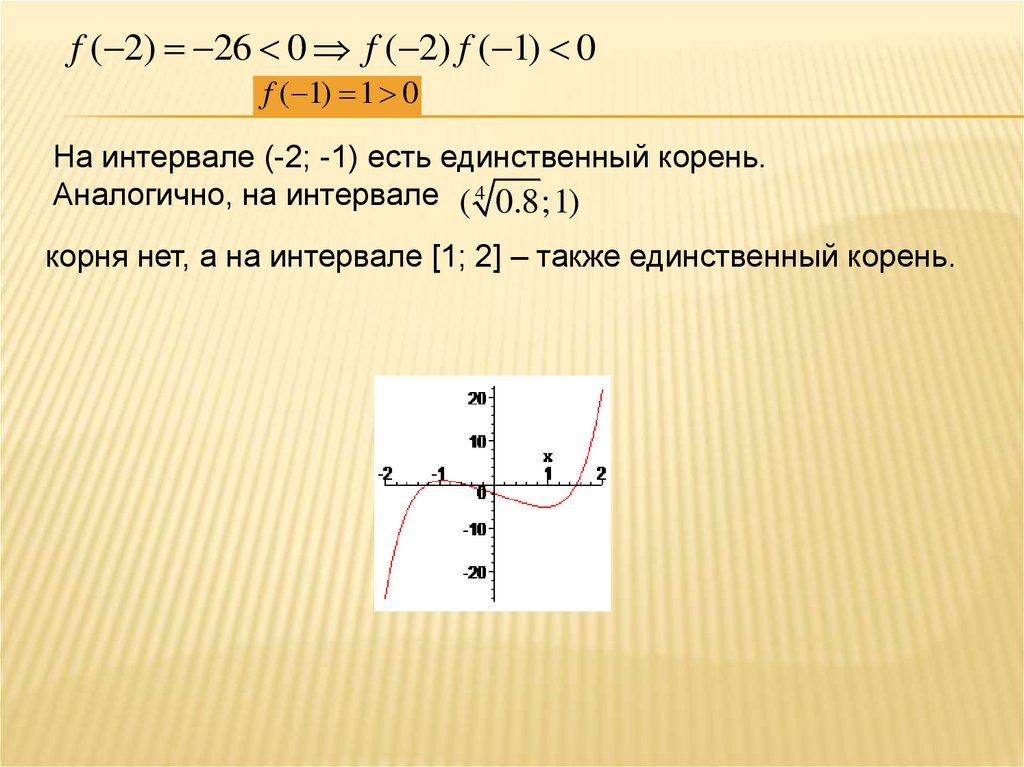
f ( 2) 26 0 f ( 2) f ( 1) 0
f ( 1) 1 0
На интервале (-2; -1) есть единственный корень.
Аналогично, на интервале ( 4 0.8;1)
корня нет, а на интервале [1; 2] – также единственный корень.

15.

3.2. Методы уточнения
корней:
Деления отрезка пополам
(бисекции, дихотомии);
Хорд;
Итерации;
Ньютона.

16.

Численный метод, при котором уточняется
первоначальное грубое приближение, называется
итерационным методом или методом
последовательных приближений.
Каждый шаг этого метода называется
итерацией.
Условие окончания итерационного
процесса (нахождения значения корня с
точностью ) имеет вид:
xk 1 xk к=0, 1,2, …

17. Метод Ньютона (КАСАТЕЛЬНЫХ)

МЕТОД НЬЮТОНА (КАСАТЕЛЬНЫХ)
По определению производной
f ( x) f ( x0 )
f ( x0 )
x x0
Если х – корень уравнения, то f(x)=0.
Следовательно, f ( x ) f ( x0 )
0
x x0
или
Тогда
f ( x0 )
x x0
f ( x0 )
f ( x0 )
x x0
f ( x0 )
(1)

18. Метод Ньютона (метод касательных)

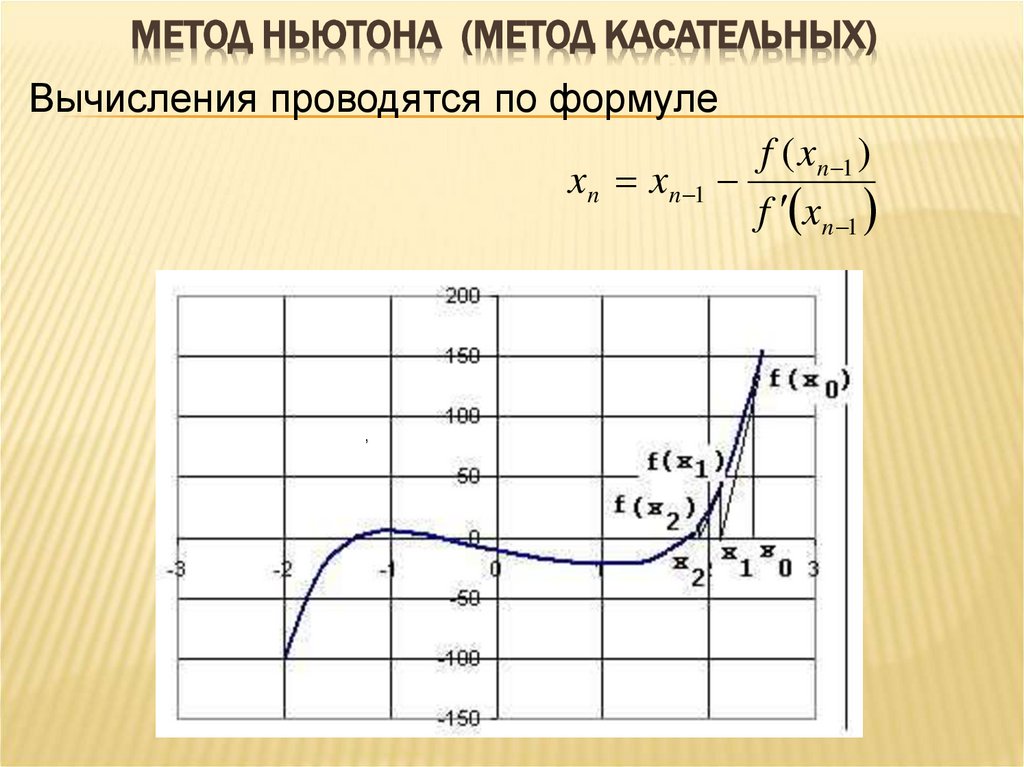
МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ)
Вычисления проводятся по формуле
f ( xn 1 )
xn xn 1
f xn 1
,

19.

Алгоритм метода Ньютона:
выбор начального приближения корня х0;
выполнение расчетов по формуле
f ( xn 1 )
xn xn 1
f xn 1
признак окончания вычислительного процесса
xn xn 1
Признак сходимости вычислительного процесса:
f ( x0 ) f ( x0 ) 0
(4)

20. Пример

ПРИМЕР
Уточнить корень уравнения
3x 3x 5 x 17 x 10 0
5
4
2
(2)
На интервале [1;2] методом Ньютона с точностью 10-1.

21. Решение

РЕШЕНИЕ
1.Находим первую и вторую производные для функции (2):
f ( x) 15x 4 12 x 3 10 x 17 (6)
f ( x) 60 x3 36 x 2 10
(7)
2. Возьмем в качестве начального приближения левую границу
интервала: x0=1.
3. Проверим условие сходимости итерационного процесса:
f ( x0 ) f ( x0 ) 0
f ( x0 ) 3 15 3 14 5 12 17 1 10 22
f ( x0 ) 60 13 36 12 10 34
f ( x0 ) f ( x0 ) ( 22) 34 0
Значение х=1 нельзя брать в качестве начального приближения!!!
3x 5 3x 4 5 x 2 17 x 10 0 (2)
xn xn 1
f ( xn 1 )
f xn 1
(3)
f ( x) 3x5 3x 4 5x 2 17 x 10
Интервал [1;2]

22. Решение

РЕШЕНИЕ
4. Возьмем в качестве начального приближения правую границу
интервала: x0=2.
5. Проверим условие сходимости итерационного процесса:
f ( x0 ) f ( x0 ) 0
f ( x0 ) 3 25 3 2 4 5 2 2 17 2 10 24
f ( x0 ) 60 23 36 2 2 10 634
f ( x0 ) f ( x0 ) 24 634 0
Значение х=2 можно взять в качестве начального приближения!!!
3x 5 3x 4 5 x 2 17 x 10 0 (5)
f ( x) 15x 4 12 x 3 10 x 17 (6)
f ( x) 60 x3 36 x 2 10 (7)
f ( x) 3x5 3x 4 5x 2 17 x 10
Интервал [1;2]

23. Решение

РЕШЕНИЕ
6. Первая итерация.
x0=2.
6.1. По формуле (3) находим следующее значение х:
f ( x0 )
3 25 3 24 5 22 17 2 10
x1 x0
2
1,837
4
3
f x0
15 2 12 2 10 2 17
6.2. Проверяем условие сходимости итерационного процесса:
xk 1 xk
У нас:
x1 x0 2 1,837 0,163 0.1
f ( x) 3x5 3x 4 5x 2 17 x 10
f ( x) 15x 4 12 x 3 10 x 17
xn xn 1
f ( xn 1 )
f xn 1
(3)

24. Решение

РЕШЕНИЕ
7. Вторая итерация.
x1=1,837.
7.1. По формуле (3) находим следующее значение х:
f ( x1 )
3 1,8375 3 1,837 4 5 1,837 2 17 1,837 10
x2 x1
2
1,957
4
3
f x1
15 1,837 12 1,837 10 1,837 17
7.2. Проверяем условие сходимости итерационного процесса:
xk 1 xk
У нас:
x2 x1 1,837 1,957 0,12 0.1
f ( x) 3x5 3x 4 5x 2 17 x 10
f ( x) 15x 4 12 x 3 10 x 17
xn xn 1
f ( xn 1 )
f xn 1
(3)

25. Решение

РЕШЕНИЕ
8. Третья итерация.
x1=1,957.
8.1. По формуле (3) находим следующее значение х:
f ( x2 )
3 1,9575 3 1,957 4 5 1,957 2 17 1,957 10
x3 x2
2
1,864
4
3
f x2
15 1,957 12 1,957 10 1,957 17
8.2. Проверяем условие сходимости итерационного процесса:
xk 1 xk
У нас:
x3 x2 1,864 1,957 0,093 0.1
Значение х = 1,864
f ( x) 3x5 3x 4 5x 2 17 x 10
f ( x) 15x 4 12 x 3 10 x 17
xn xn 1
f ( xn 1 )
f xn 1
(3)

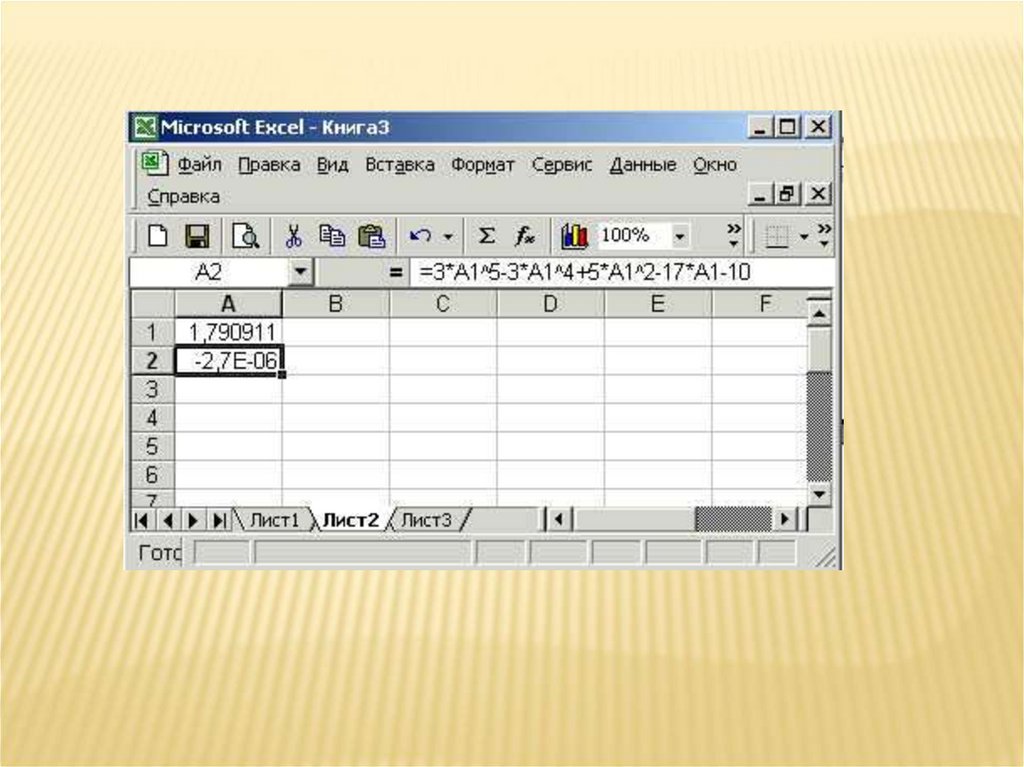
26. Метод Ньютона. РЕШЕНИЕ В Excel с точностью 10-3

МЕТОД НЬЮТОНА. РЕШЕНИЕ В EXCEL С ТОЧНОСТЬЮ 10-3
f ( x) 3x5 3x 4 5x 2 17 x 10
f ( x) 15x 4 12 x 3 10 x 17
Метод Ньютона
f ( xn 1 )
xn xn 1
f xn 1
Проверка точности
вычислений
xk 1 xk

27. Метод Ньютона. MathCAD. функция “root”.

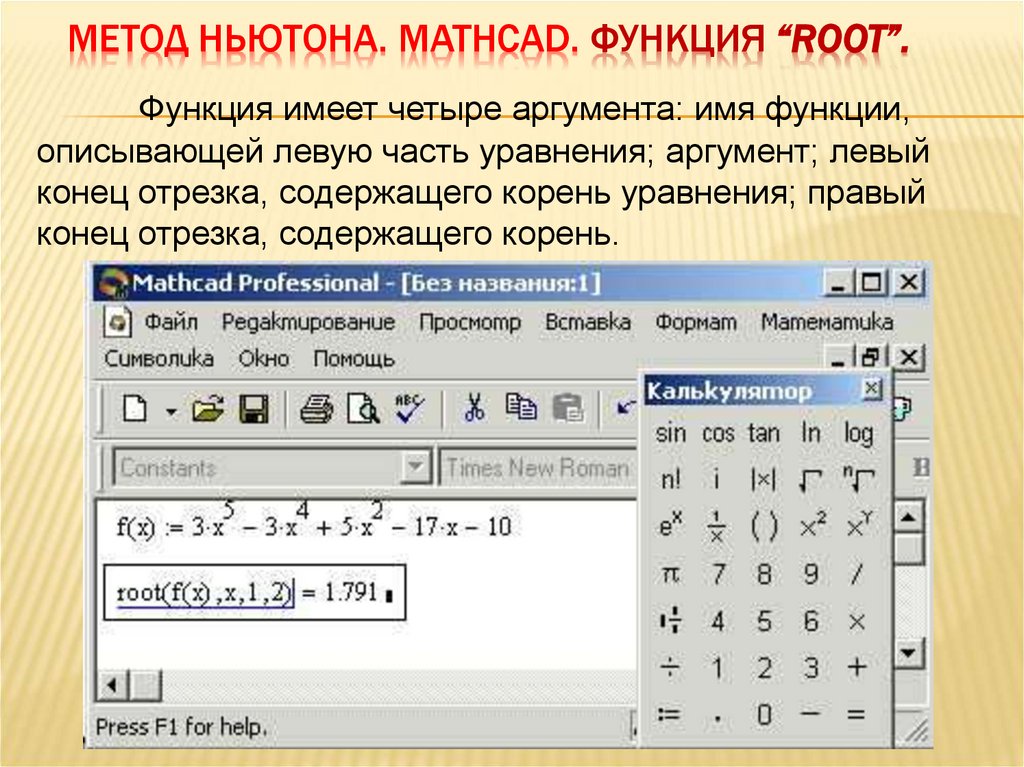
МЕТОД НЬЮТОНА. MATHCAD. ФУНКЦИЯ “ROOT”.
Функция имеет четыре аргумента: имя функции,
описывающей левую часть уравнения; аргумент; левый
конец отрезка, содержащего корень уравнения; правый
конец отрезка, содержащего корень.

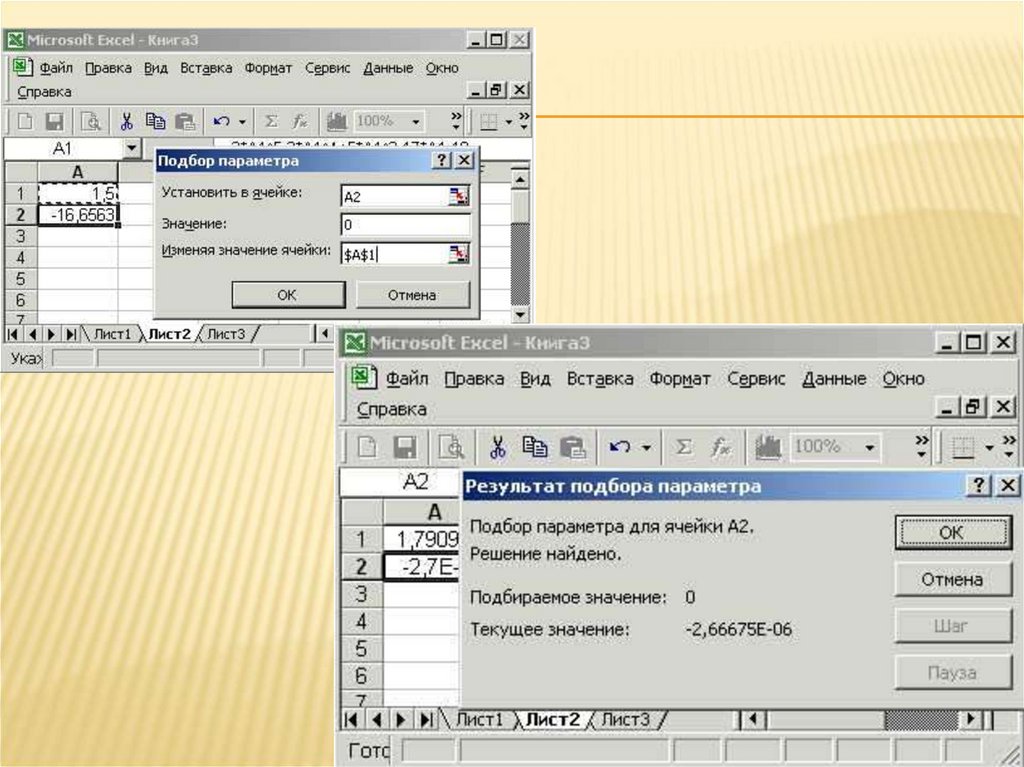
28. Команда «Подбор параметра»

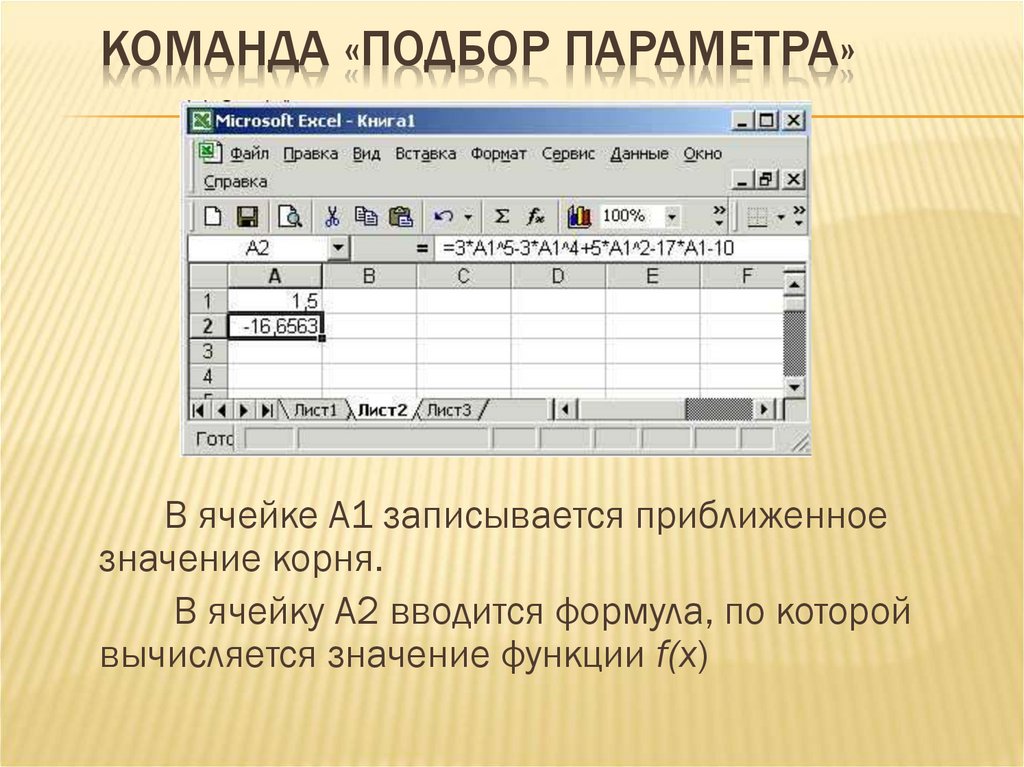
КОМАНДА «ПОДБОР ПАРАМЕТРА»
В ячейке А1 записывается приближенное
значение корня.
В ячейку А2 вводится формула, по которой
вычисляется значение функции f(x)

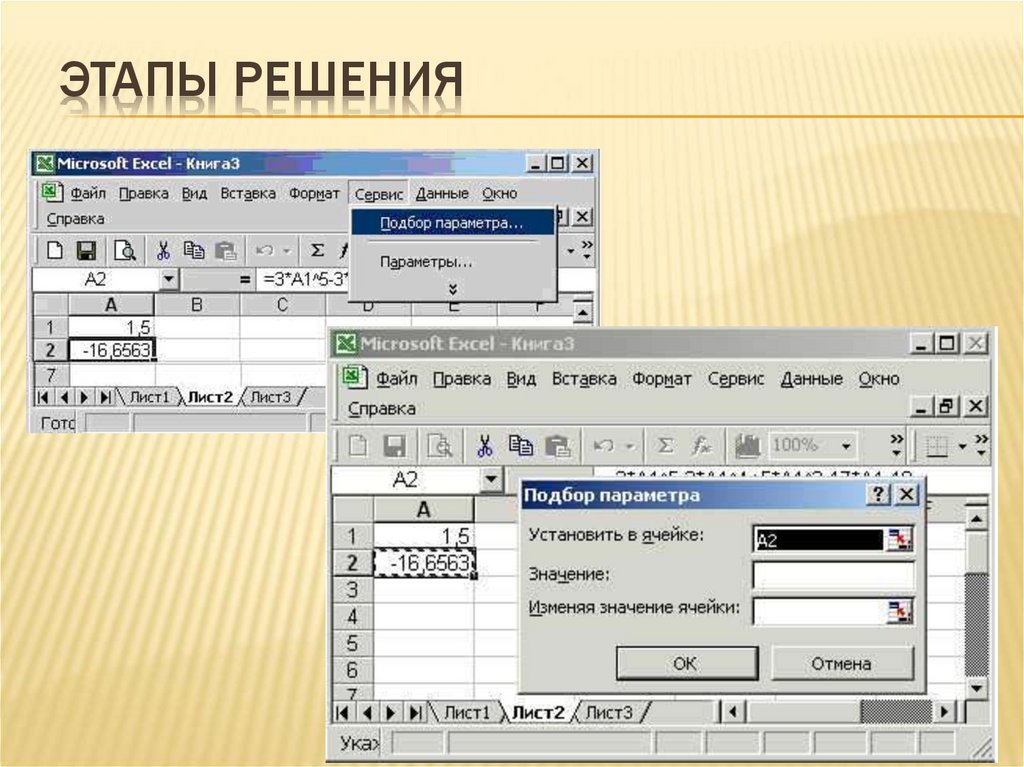
29. Этапы решения

ЭТАПЫ РЕШЕНИЯ

30.

31.

32.

Вопрос из теста
При уточнении корня уравнения на заданном
отрезке по методу Ньютона получены значения
корня на трех итерациях:
6,072; 6,076; 6,079.
Определите погрешность вычисления
1. 0,003.
2. 0,1
3. 0,06.
4. 0,004.

33.

4. Численные методы решения
обыкновенных
дифференциальных уравнений

34.

МЕТОД ЭЙЛЕРА
Решение задачи Коши методом Эйлера
Пусть требуется найти на отрезке [a, b]
решение дифференциального уравнения 1-го
порядка
y f ( x, y )
с начальным условием
y( x0 ) y0
(задача Коши).
(2)
(1)

35. Численное решение

ЧИСЛЕННОЕ РЕШЕНИЕ
При численном решении уравнения задача
ставится так:
найти в точках
x0, x1, x2,…xn
приближения
y0, y1, y2,… yn
для точного решения
y(x0), y(x1), y(x2), .. y(xn)
Разность между
значениями аргумента х
называют шагом сетки и
чаще всего принимают
постоянным, обозначая
h.

36. Задача Коши

ЗАДАЧА КОШИ
Задача Коши (задача с начальными
условиями) есть задача о нахождении частного
решения, которое удовлетворяет начальным
условиям:
y х x x y 0
0

37.

В дифференциальном уравнении
y x f x, y x
производная y′ (х) на основании ее определения
заменяется отношением приращений функции к
приращению аргумента
y y
y x lim
f x, y x
x x
x 0

38.

Тогда
y0
f x0 , y 0
x0
Или
y y0
f x0 , y 0
x x0
Или
y y0 x x0 f x0 , y0
yn yn 1 h f xn 1 , yn 1

39.

Алгоритм метода Эйлера
Отрезок, на котором ищется решение задачи,
разбивают на n частей с шагом
h (b a) n
и находят значения y y ( x )
k
k
в точках
xk x0 kh, (k 0,1,..., n)
Очевидно, что при этом x0 a, xn b
Значения yk 1
определяют по формуле
yk 1 yk hf ( xk , yk ), k 0,1, 2..., n 1
(3)

40.

Пример.
Решить задачу Коши для обыкновенного
дифференциального уравнения 1-го порядка методом
Эйлера.
Вычисления выполнять с четырьмя десятичными
знаками на отрезке [0,2; 1,2] с шагом 0,1.
Уравнение:
y 0,185( x 2 cos 0,7 x) 1,843 y
Начальное условие:
y (0, 2) 0, 25
(5)
(4)

41.

Для численного решения заданного уравнения
вида (4) с начальным условием (5) нам потребуется
выполнить
n (b a) h (1, 2 0, 2) 0,1 10 шагов.
На каждом шаге надо вычислить значения
xk ,
yk ,
yk f ( xk , yk ),
[a; b] = [0,2; 1,2]
h yk и yk 1
h=0.1
y 0,185( x 2 cos 0,7 x) 1,843 y (4)
y (0, 2) 0, 25 (5)

42.

Первый шаг. (k = 0). Имеем:
x0 a 0, 2;
По формуле
(3)формуле (4)
По
y0 y( x0 ) 0, 25; h 0,1
y1 y0 hf ( x0 , y0 ) (6)
f ( x0 , y0 ) 0,185 0, 22 cos(0, 7 0, 2) 1,843 0, 25 0, 6513
Тогда
hf ( x0 , y0 ) 0,1 0, 6513 0, 0651
и, следовательно, по формуле (6)
y1 0, 25 0,0651 0,3151
yk 1 yk hf ( xk , yk ), k 0,1, 2..., n 1 (3)
[a; b] = [0,2; 1,2]
h=0.1
y 0,185( x 2 cos 0, 7 x) 1,843 y (4)
n=10
y (0, 2) 0, 25 (5)

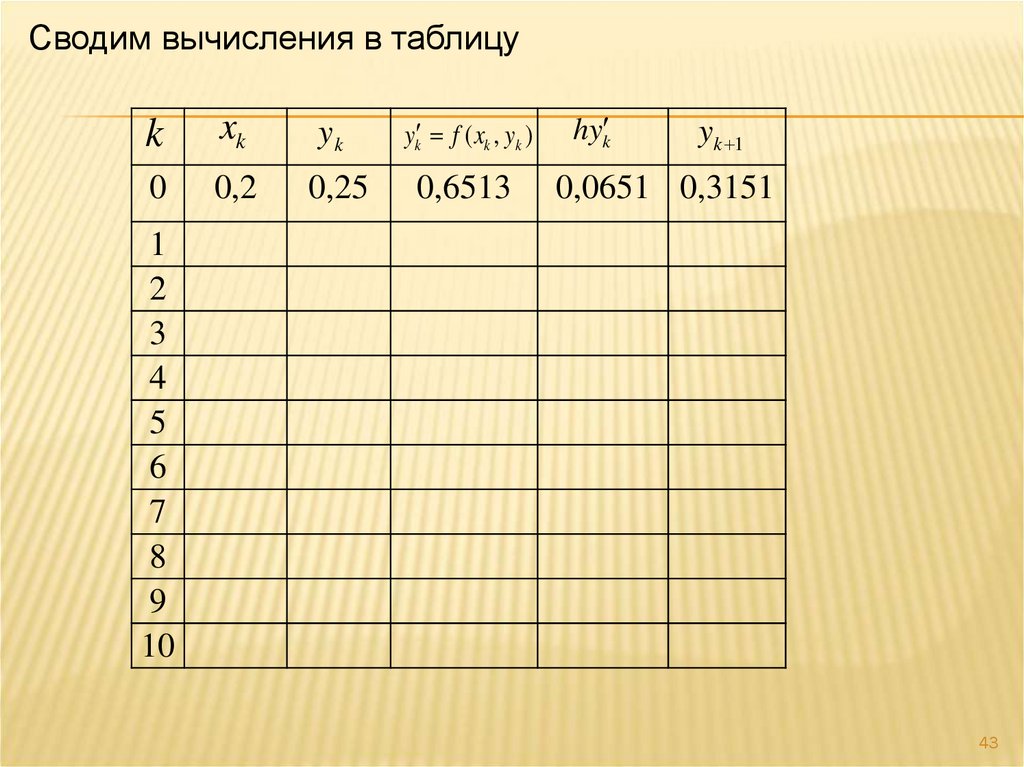
43.

Сводим вычисления в таблицу
k
xk
yk
yk f ( xk , yk )
hyk
0
0,2
0,25
0,6513
0,0651 0,3151
yk 1
1
2
3
4
5
6
7
8
9
10
43

44.

Второй шаг. (k=1).
x1 x0 h 0, 2 0,1 0,3; y2 y1 hf ( x1 , y1 )
2
Вычислим f ( x1 , y1 ) 0,185(0,3 cos(0, 7 0,3)) 1,843 0,3151 0, 7784
Тогд
а
hf ( x1 , y1 ) 0,1 0,7784 0,0778
k
xk
0
1
2
3
4
5
6
7
8
9
10
0,2
и y2 0,3151 0,0778 0,3929
yk 1
yk
yk f ( xk , yk )
hyk
0,25 0,6513 0,0651 0,3151
44

45.

Второй шаг. (k=1).
x1 x0 h 0, 2 0,1 0,3; y2 y1 hf ( x1 , y1 )
2
Вычислим f ( x1 , y1 ) 0,185(0,3 cos(0, 7 0,3)) 1,843 0,3151 0, 7784
Тогд
а
hf ( x1 , y1 ) 0,1 0,7784 0,0778
k
xk
0
1
2
3
4
5
6
7
8
9
10
0,2
0,3
и y2 0,3151 0,0778 0,3929
yk 1
yk
yk f ( xk , yk )
hyk
0,25 0,6513 0,0651 0,3151
0,351 0,7784 0,0778 0,3929
45

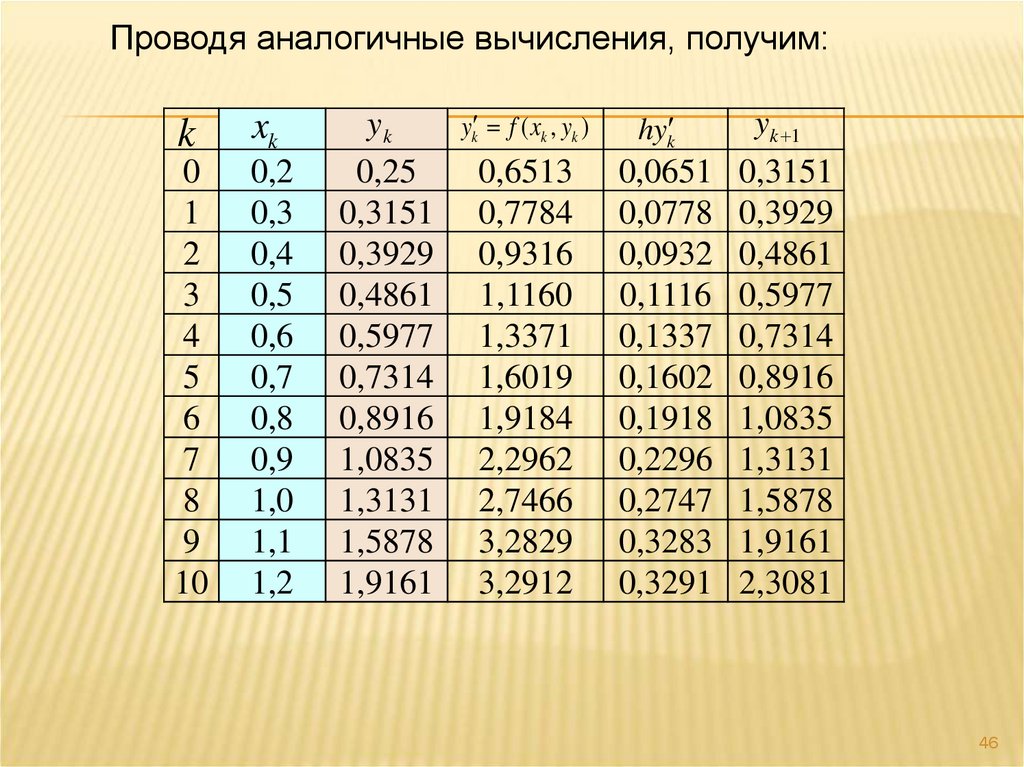
46.

Проводя аналогичные вычисления, получим:
k
xk
0
1
2
3
4
5
6
7
8
9
10
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
yk
0,25
0,3151
0,3929
0,4861
0,5977
0,7314
0,8916
1,0835
1,3131
1,5878
1,9161
yk f ( xk , yk )
hyk
0,6513
0,7784
0,9316
1,1160
1,3371
1,6019
1,9184
2,2962
2,7466
3,2829
3,2912
0,0651
0,0778
0,0932
0,1116
0,1337
0,1602
0,1918
0,2296
0,2747
0,3283
0,3291
yk 1
0,3151
0,3929
0,4861
0,5977
0,7314
0,8916
1,0835
1,3131
1,5878
1,9161
2,3081
46

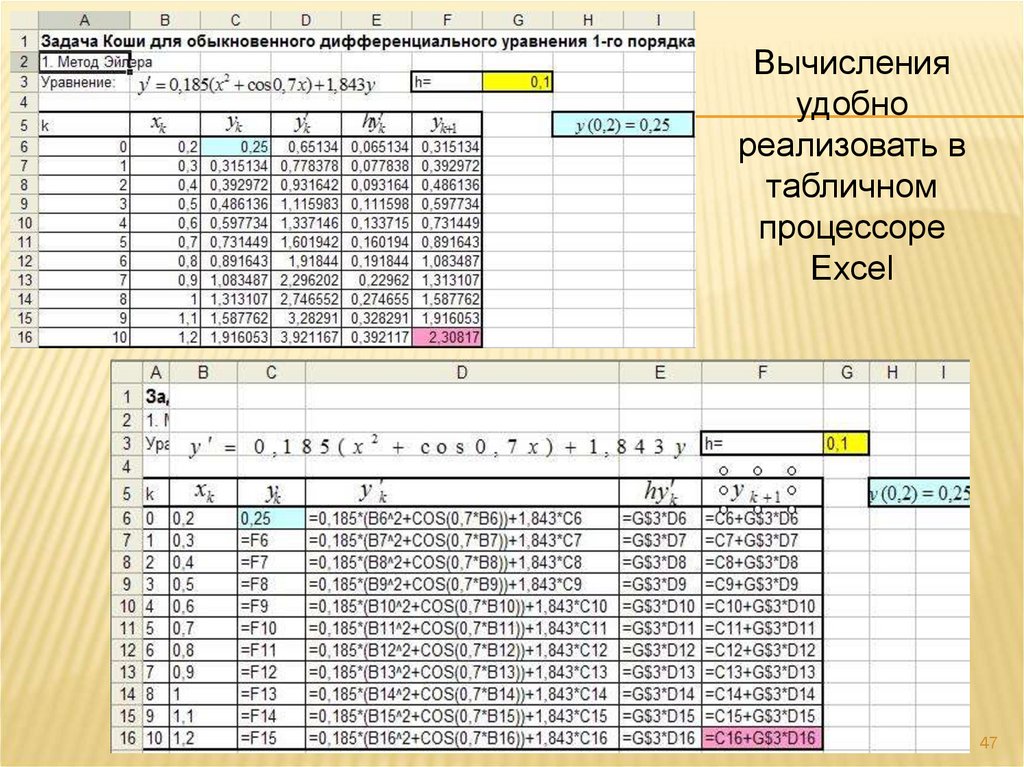
47.

Вычисления
удобно
реализовать в
табличном
процессоре
Excel
47