Похожие презентации:
Основы радиоэлектроники
1.
22 октября1
2.
23.
(3.1)(3.2)
3
4.
45.
56.
67.
Комплексные числаСправочник
ei cos i sin .
Формулы Эйлера
i
i
i
i
e
e
e
e
e i cos i sin , cos
, sin
.
2
2i
a ib a b e
2
2
a ib a 2 b2 ,
i
b
a b cos i sin , arc tg .
a
2
2
a ib
a ib
a 2 b2
.
c id
c id
c2 d 2
e x e x
e x e x
sh x
, ch x
.
2
2
sin ix = i sh x, sh ix=i sin x, cos ix = ch x, th ix = - i tg x .
7
8.
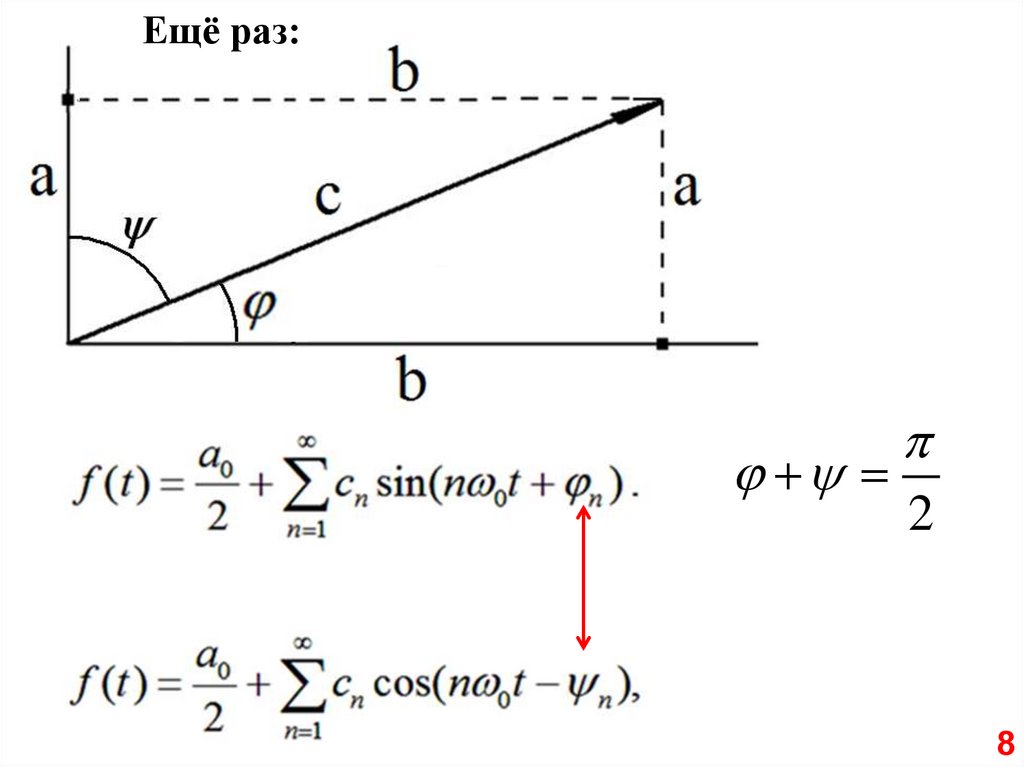
Ещё раз:2
8
9.
Умножим иразделим на i
(3.7)
9
10.
(3.7)10
11.
1112.
10слайд
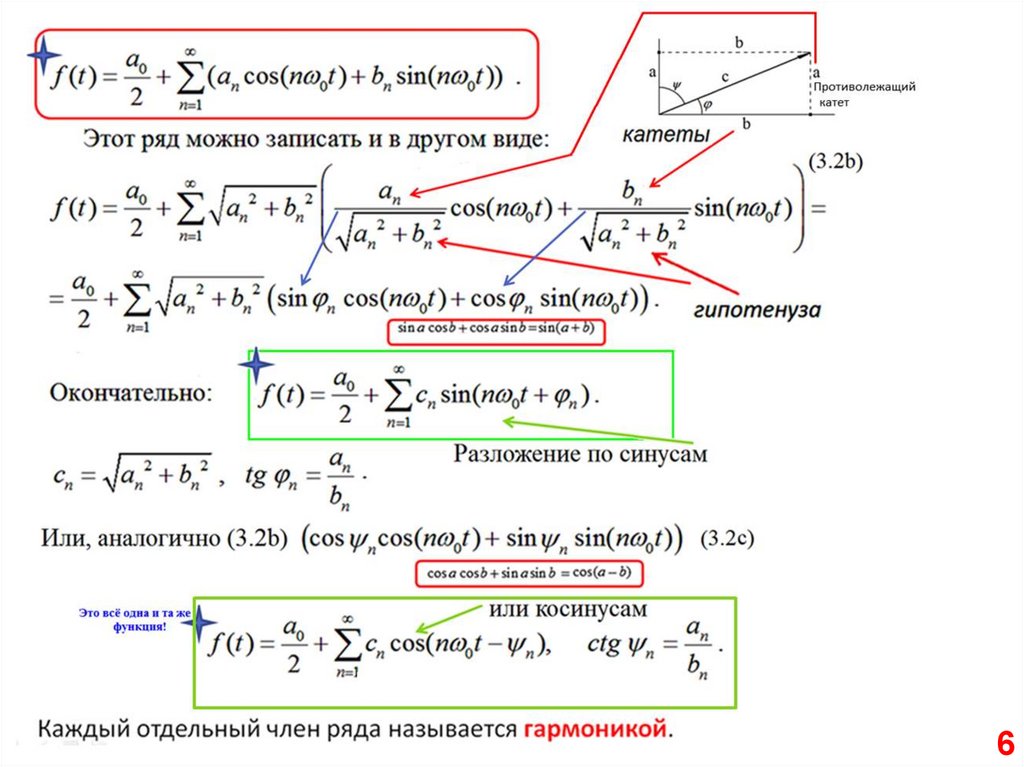
Получается, что сумма парных
комплексных гармоник есть гармоника старого, доброго,
вещественного ряда Фурье.
12
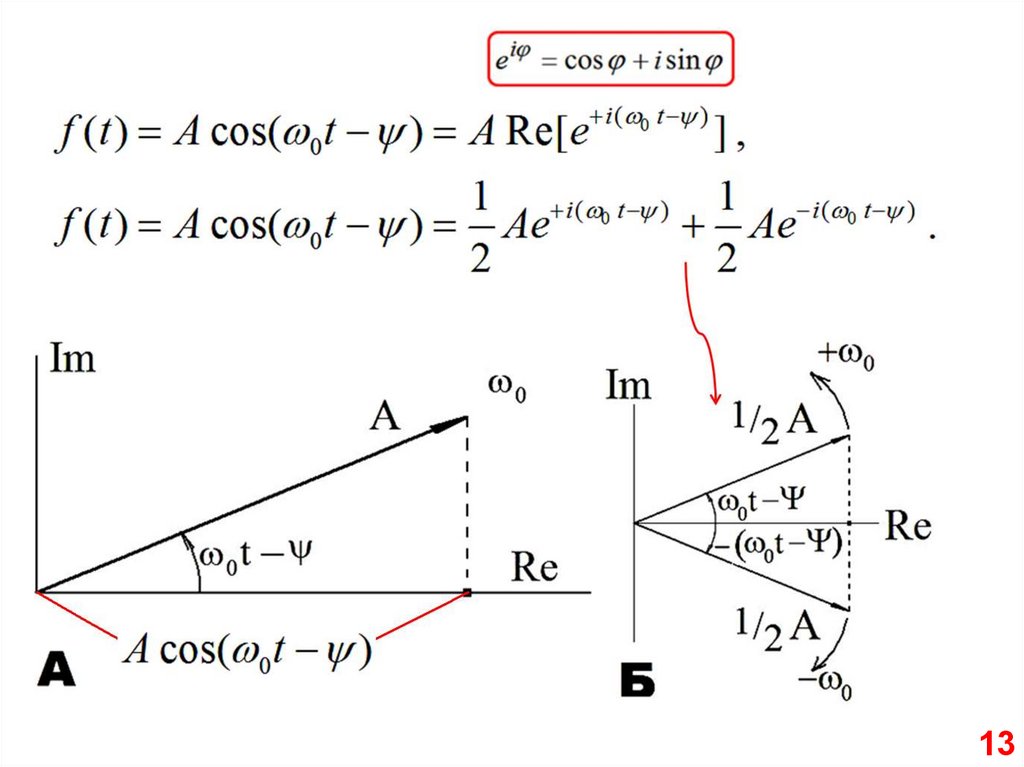
13.
1314.
1014
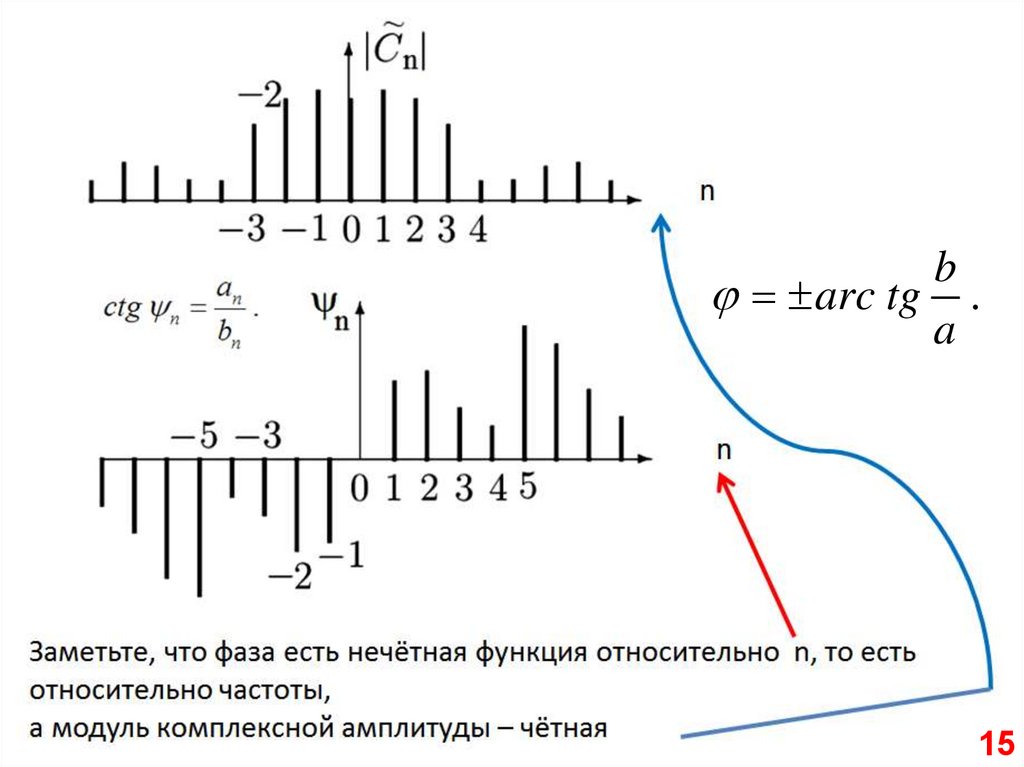
15.
barc tg .
a
15
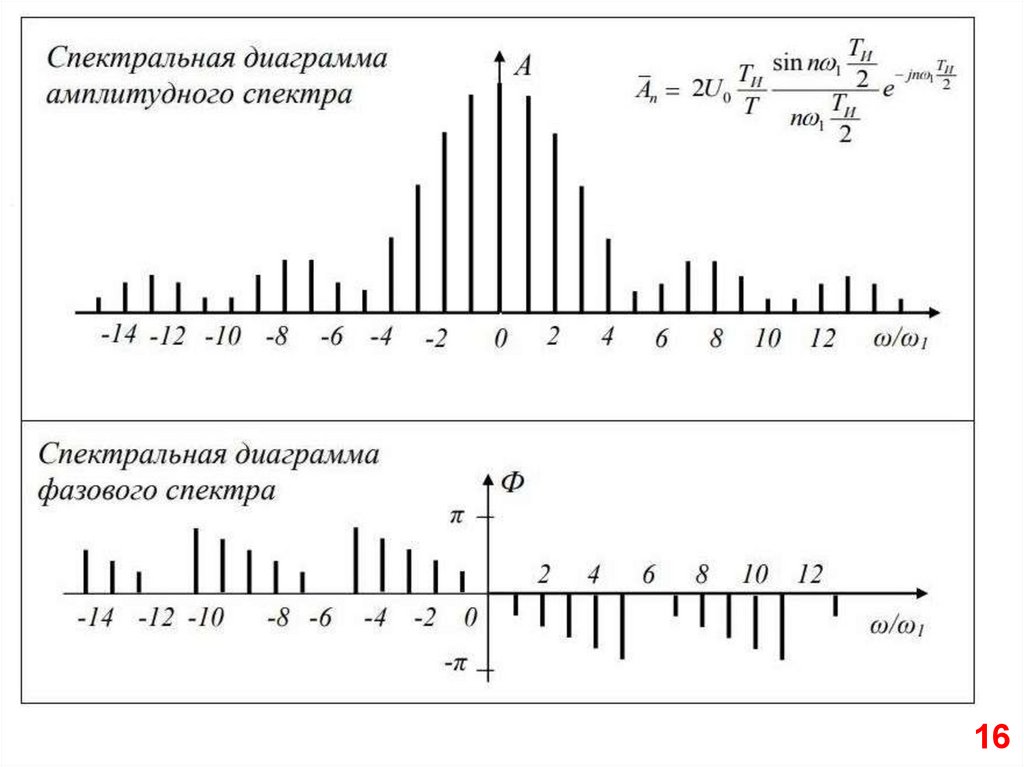
16.
1617.
1718.
1819.
1920.
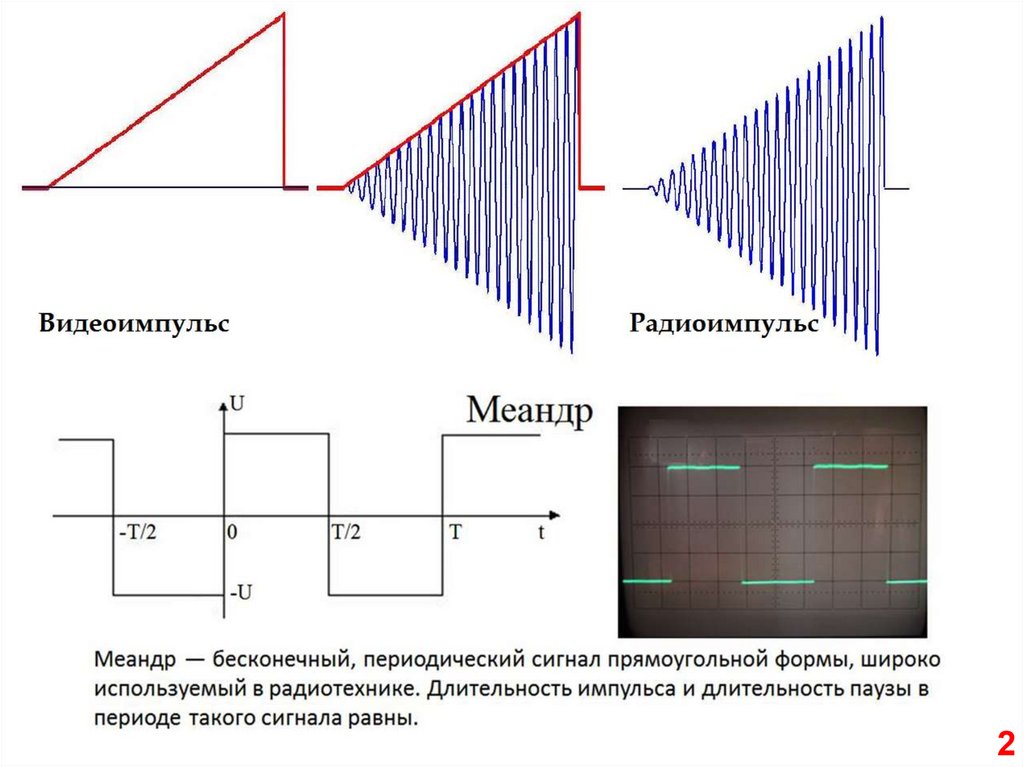
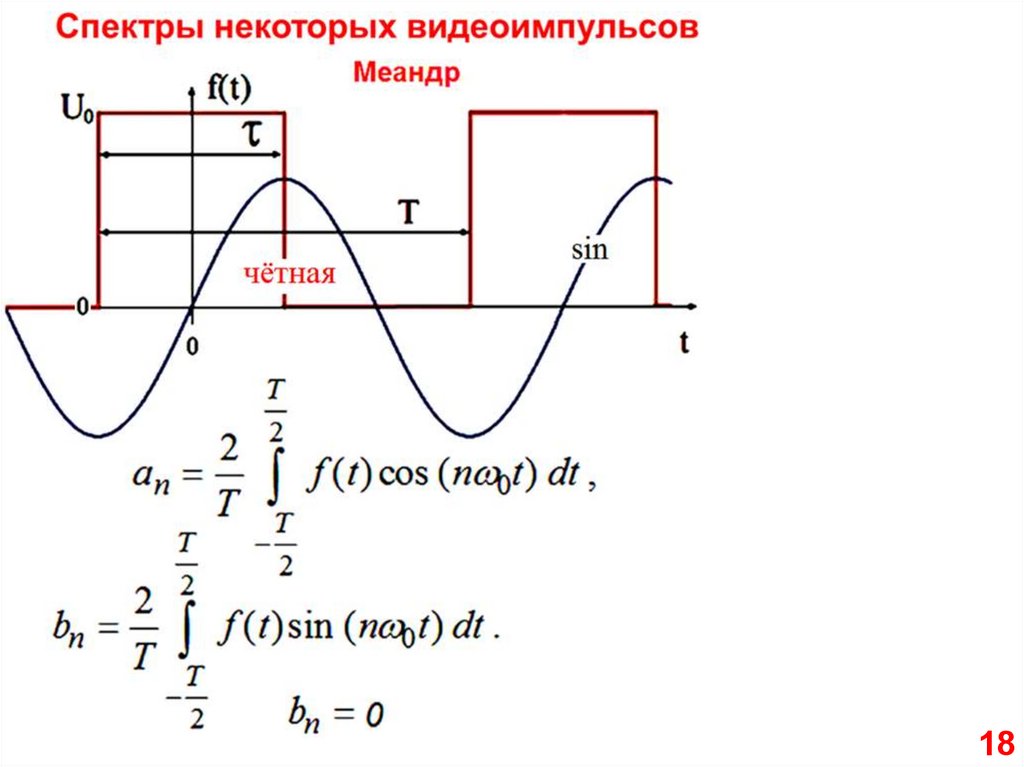
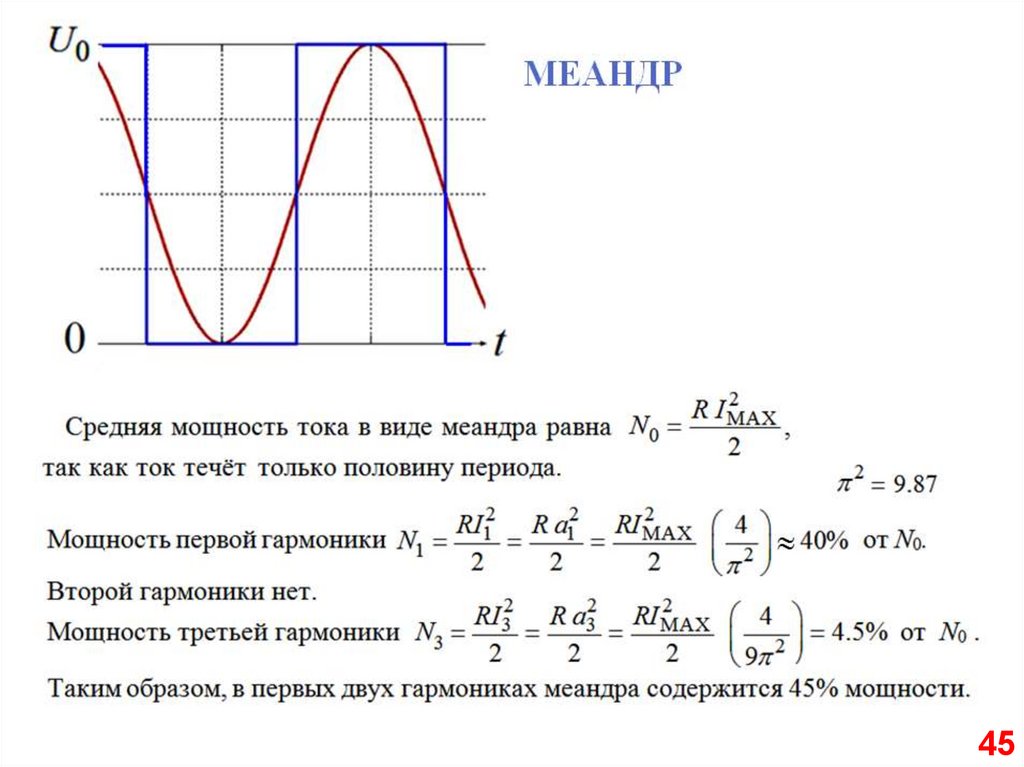
Такую функцию в радиотехникеназывают "меандр", по имени
древнегреческой реки.
Длительность импульса равна
1
половине периода
T 2
.
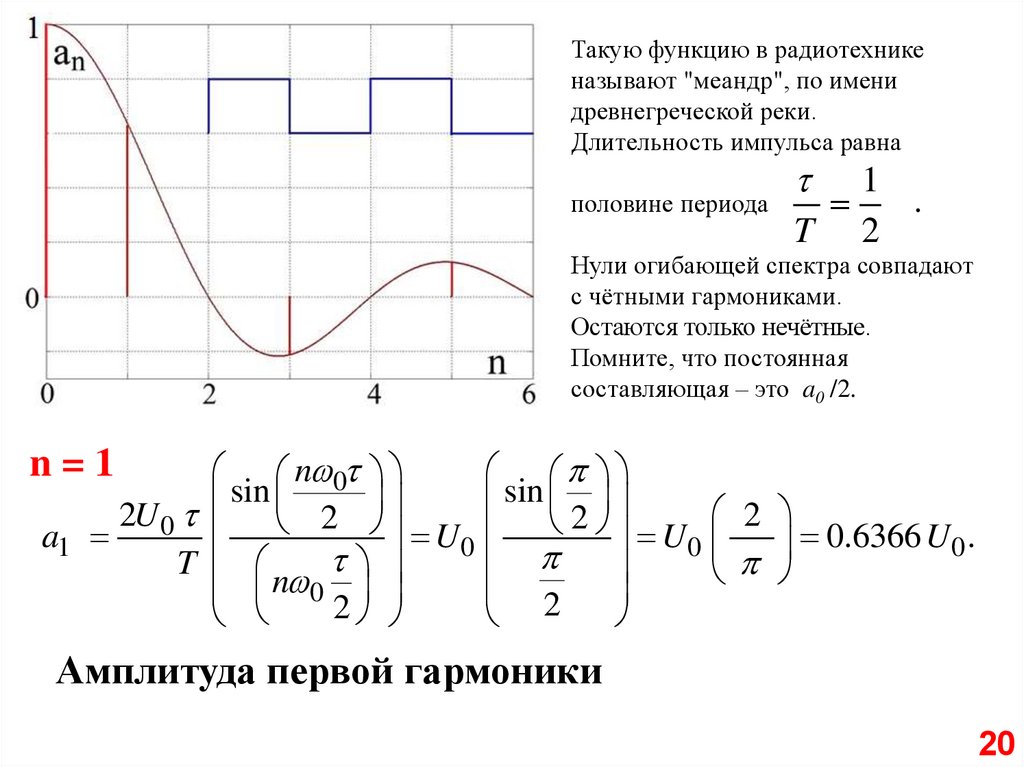
Нули огибающей спектра совпадают
с чётными гармониками.
Остаются только нечётные.
Помните, что постоянная
составляющая – это a0 /2.
n 0
sin
sin
2
2U 0
2
2
a1
U0
U0
0.6366 U 0 .
T
n
0 2
2
n=1
Амплитуда первой гармоники
20
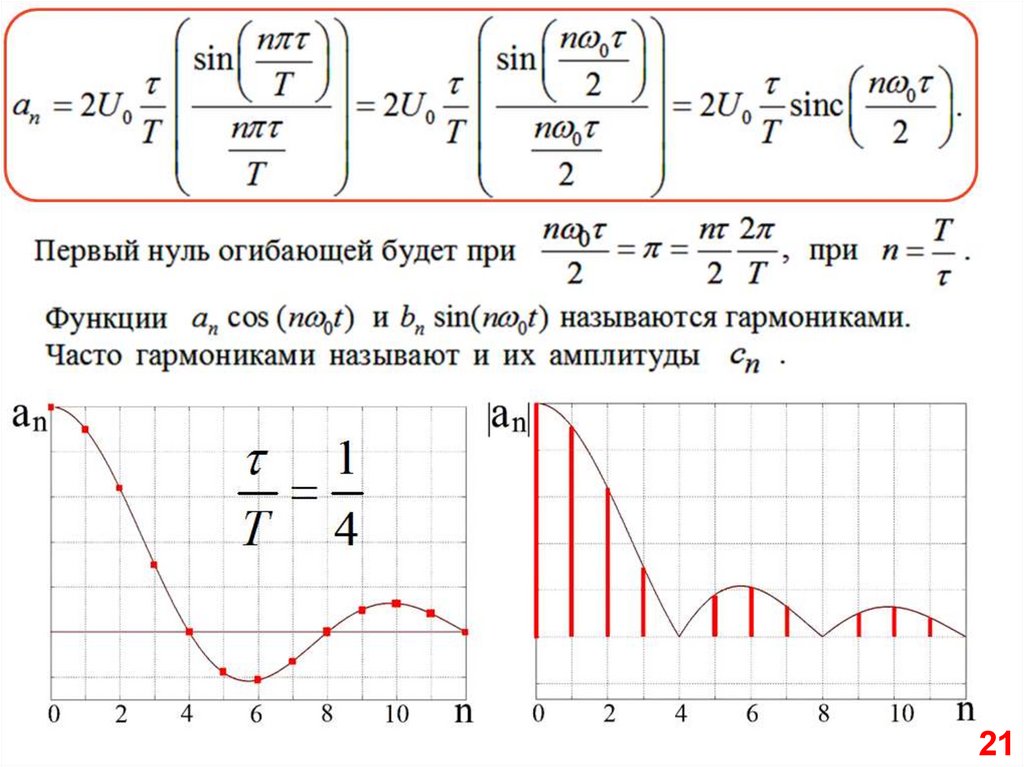
21.
2122.
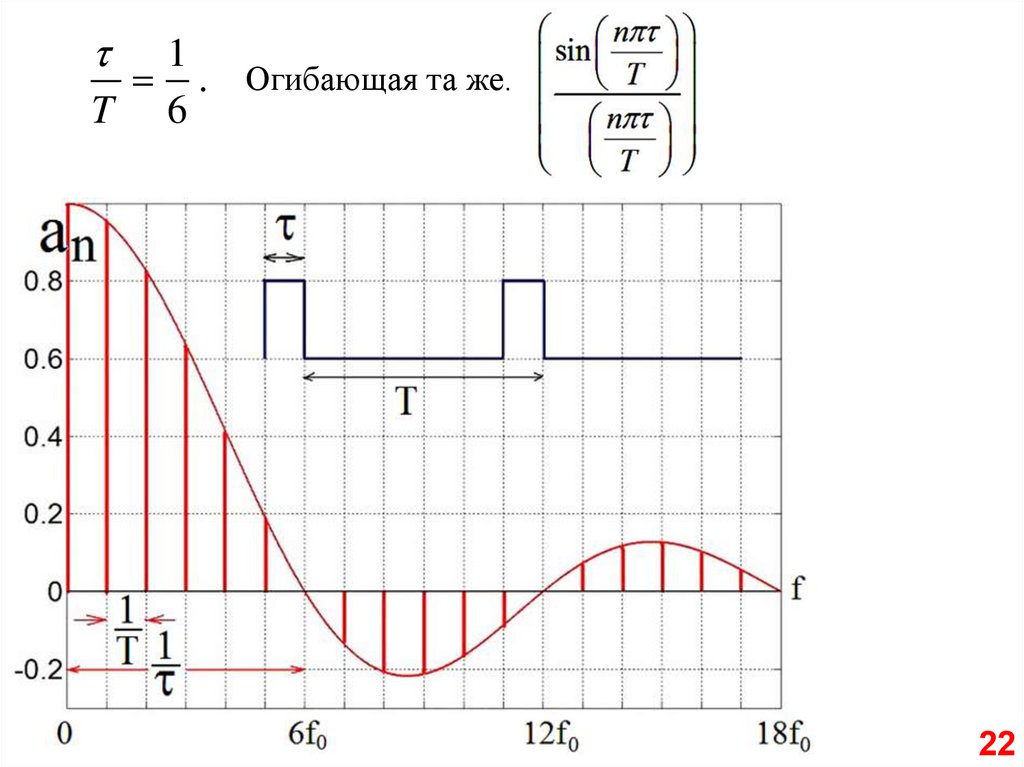
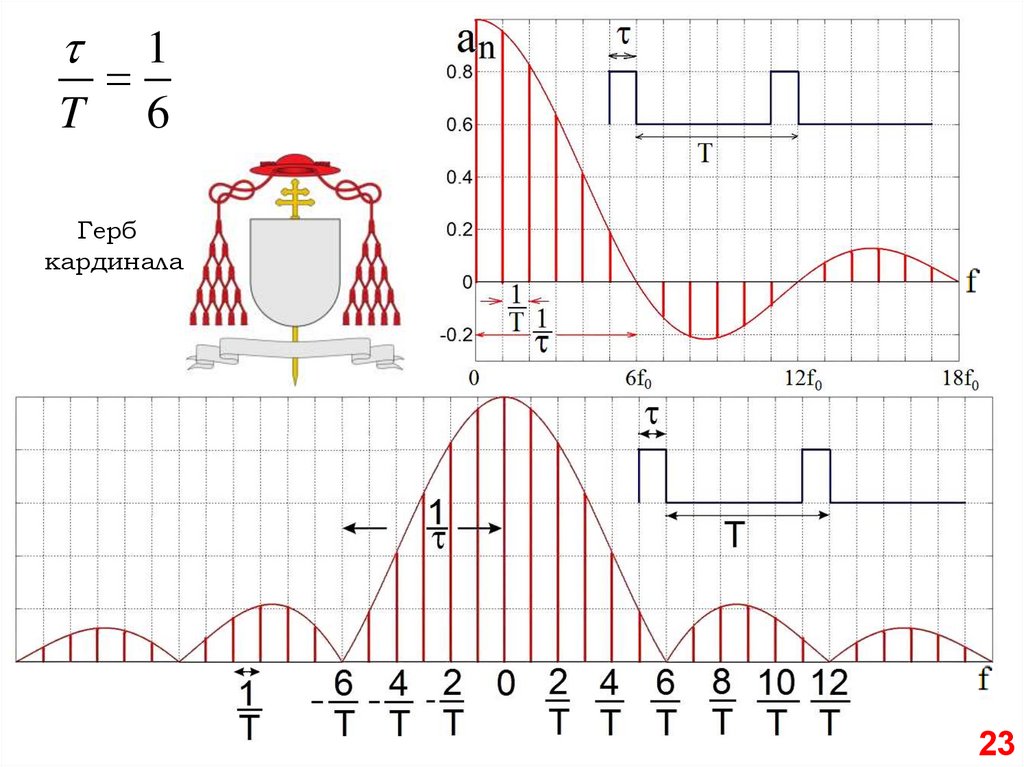
1. Огибающая та же.
T 6
22
23.
1T 6
Герб
кардинала
23
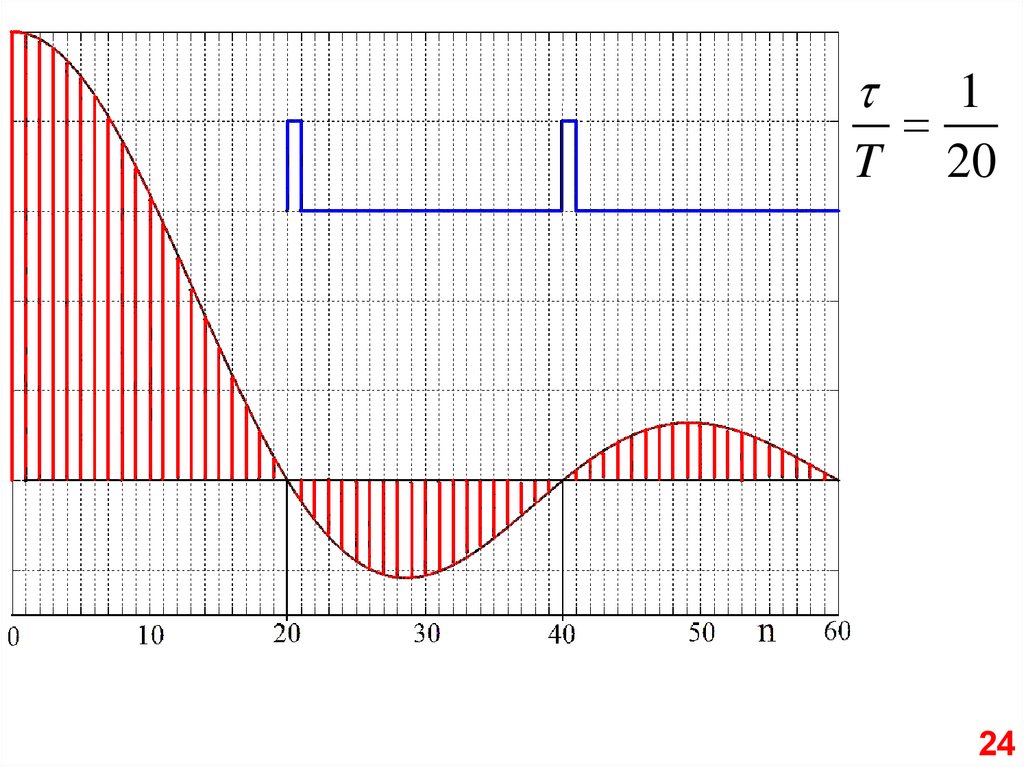
24.
1T 20
24
25.
2526.
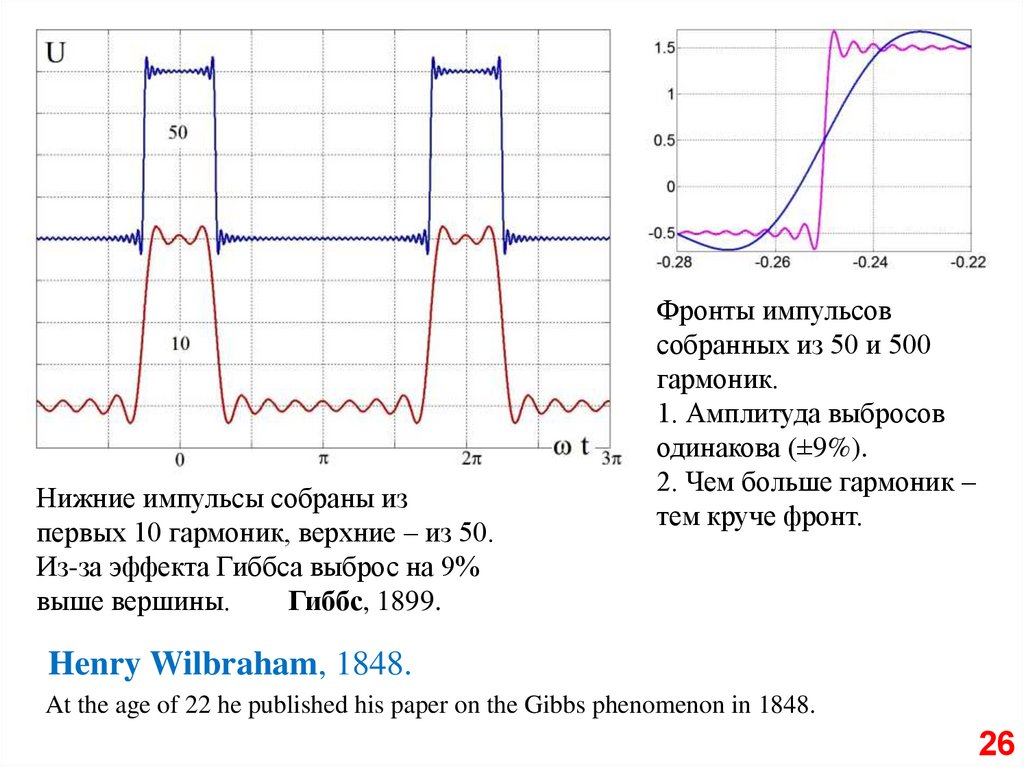
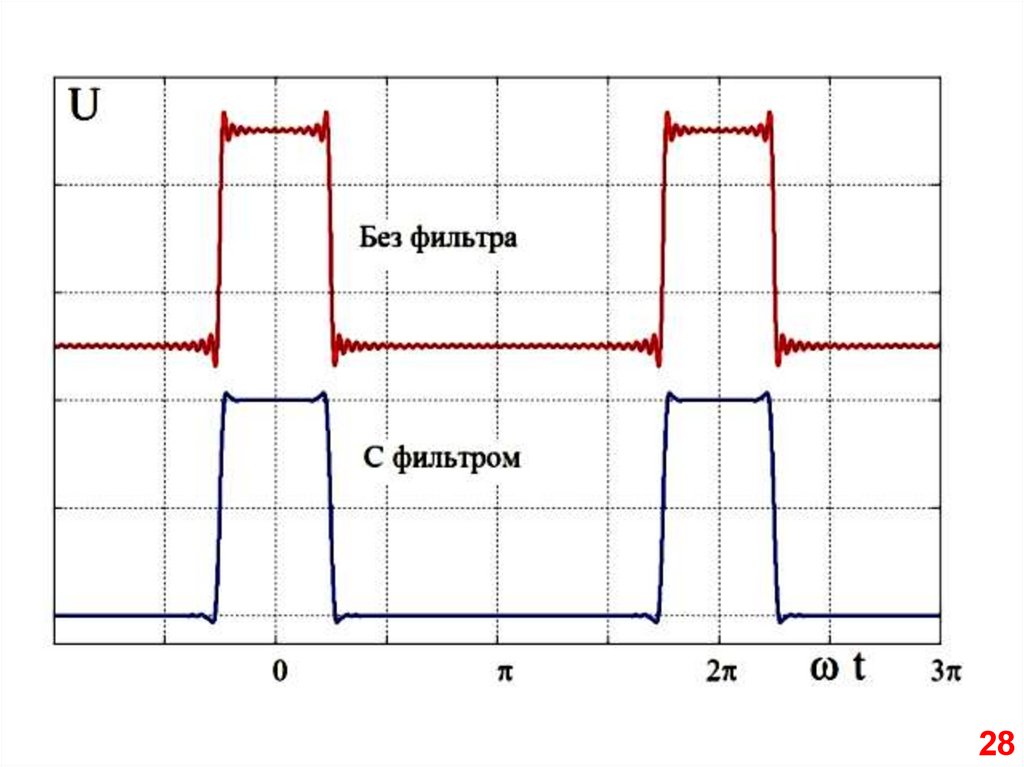
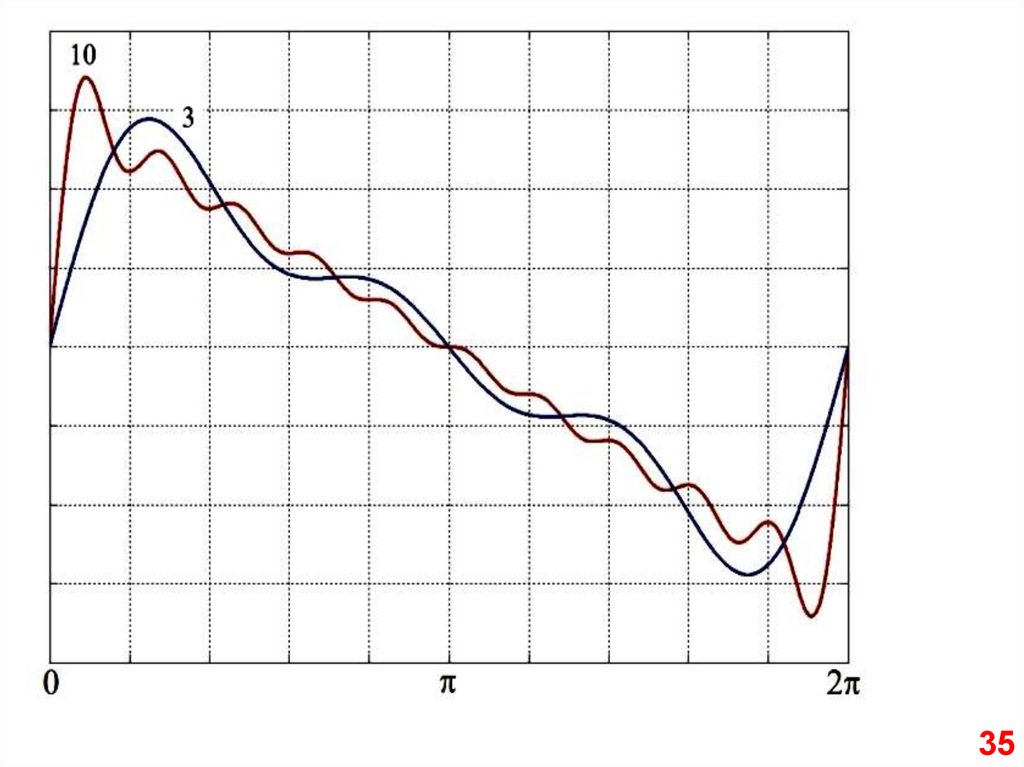
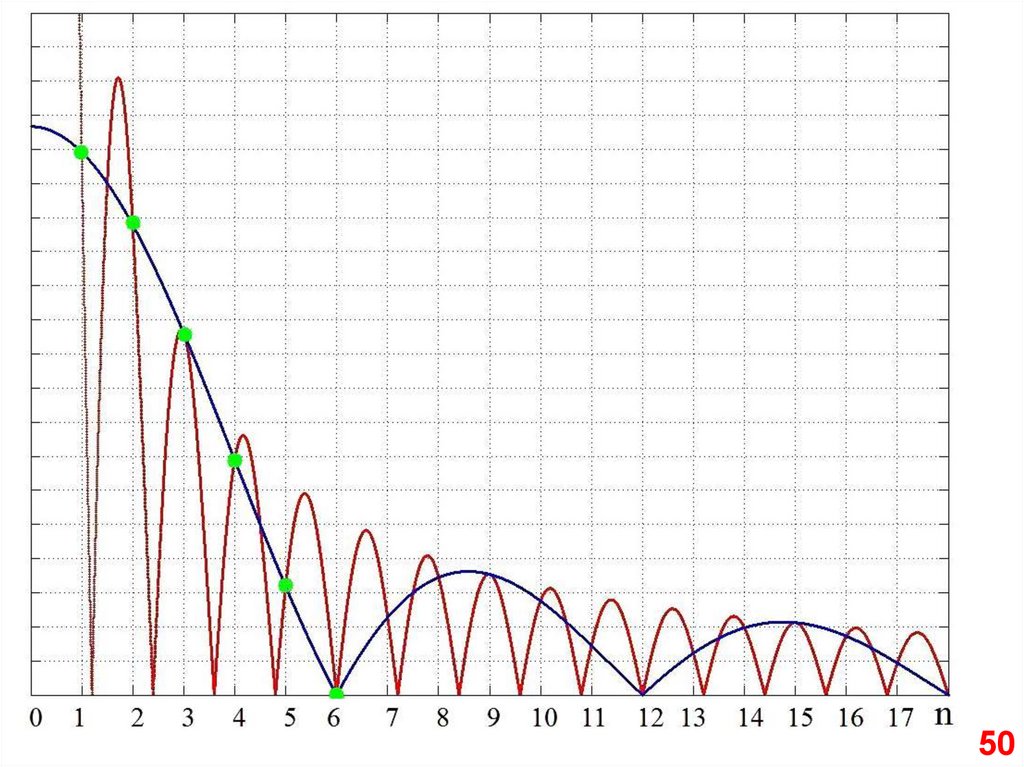
Нижние импульсы собраны изпервых 10 гармоник, верхние – из 50.
Из-за эффекта Гиббса выброс на 9%
выше вершины.
Гиббс, 1899.
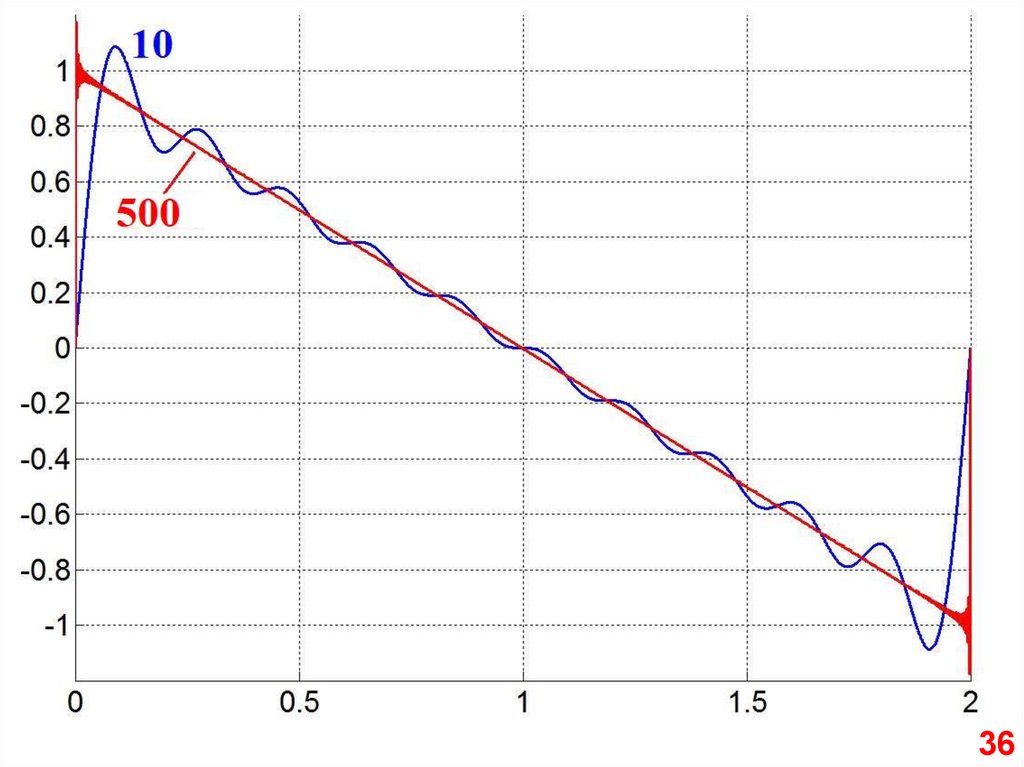
Фронты импульсов
собранных из 50 и 500
гармоник.
1. Амплитуда выбросов
одинакова (±9%).
2. Чем больше гармоник –
тем круче фронт.
Henry Wilbraham, 1848.
At the age of 22 he published his paper on the Gibbs phenomenon in 1848.
26
27.
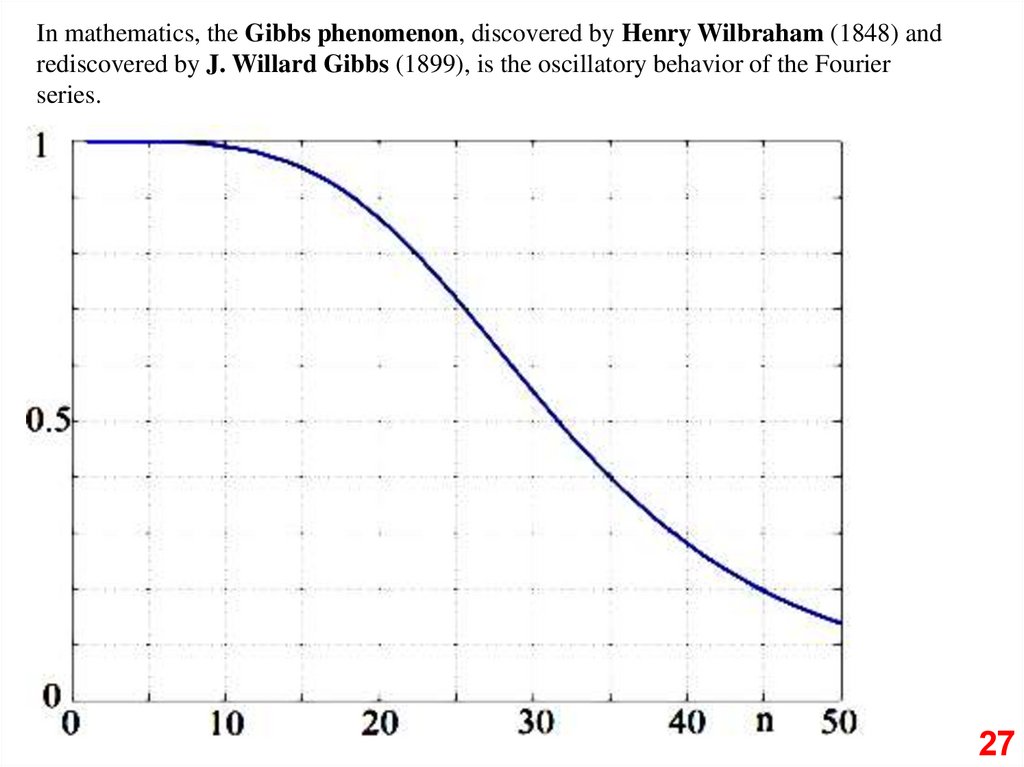
In mathematics, the Gibbs phenomenon, discovered by Henry Wilbraham (1848) andrediscovered by J. Willard Gibbs (1899), is the oscillatory behavior of the Fourier
series.
27
28.
2829.
2930.
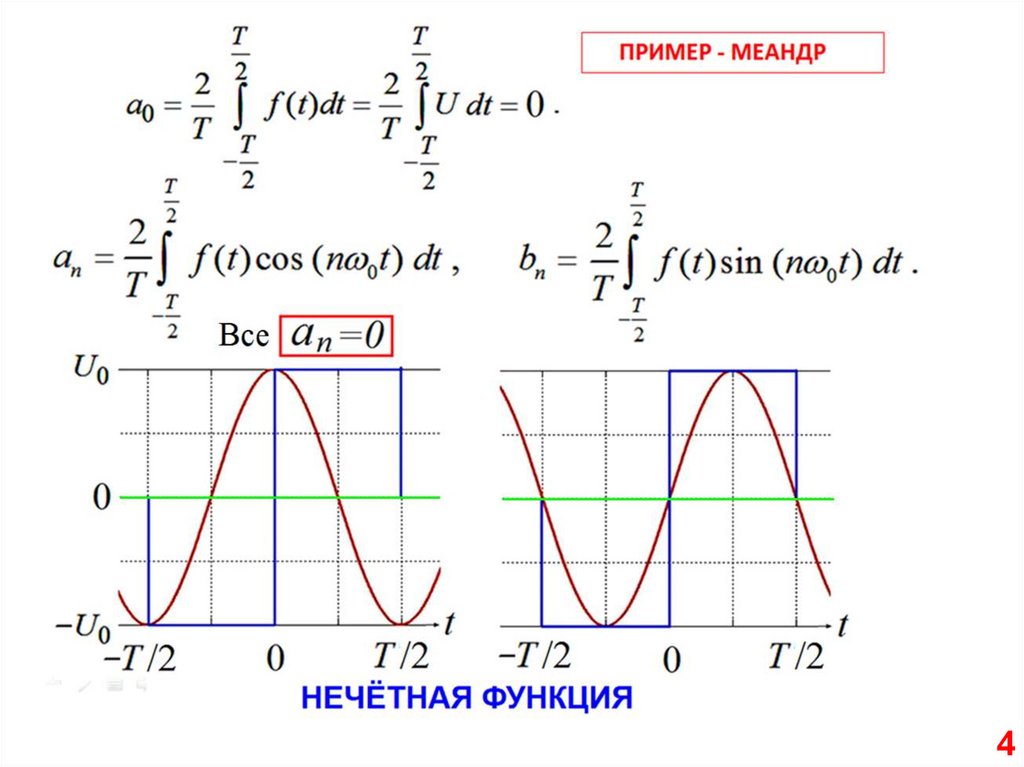
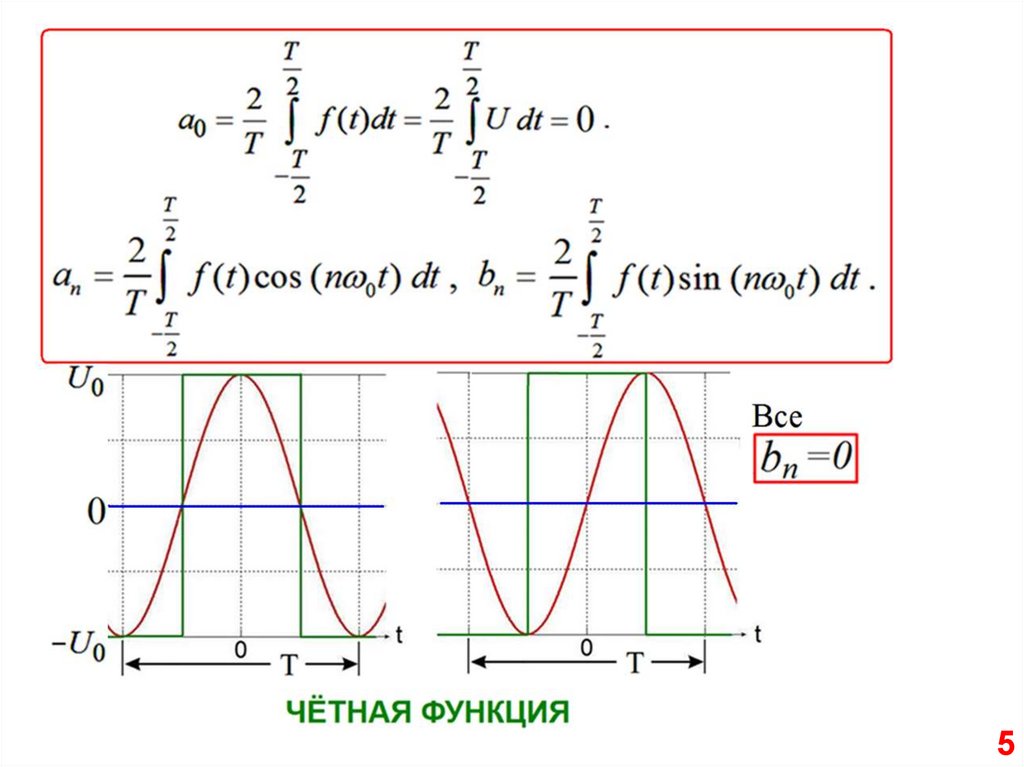
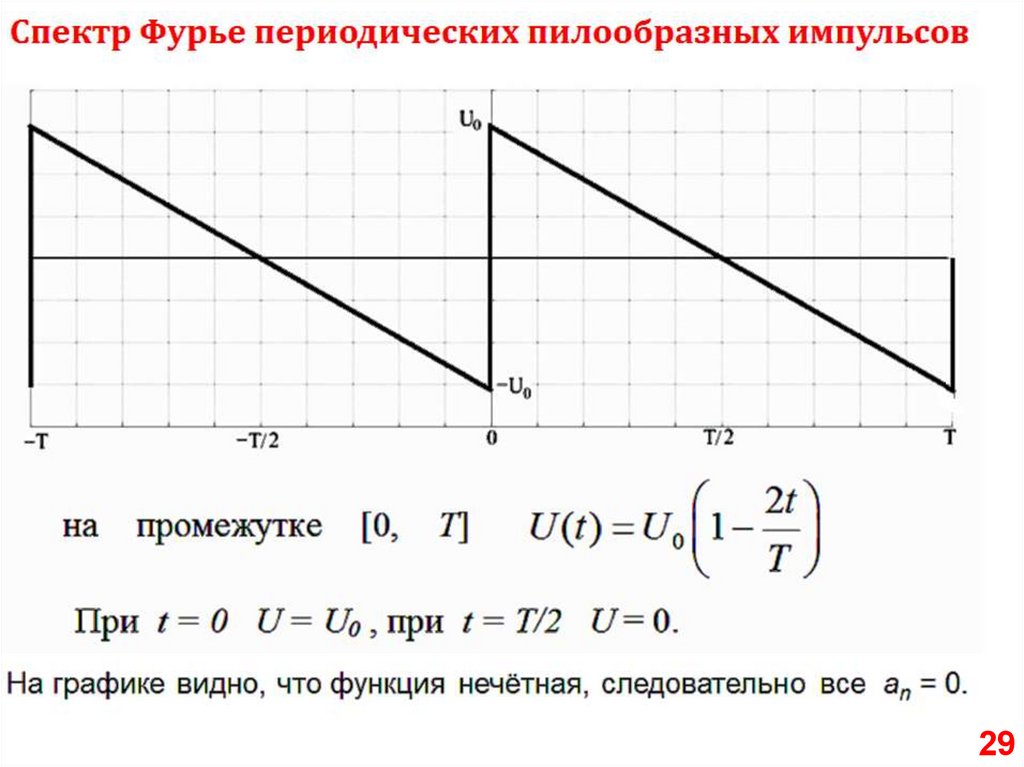
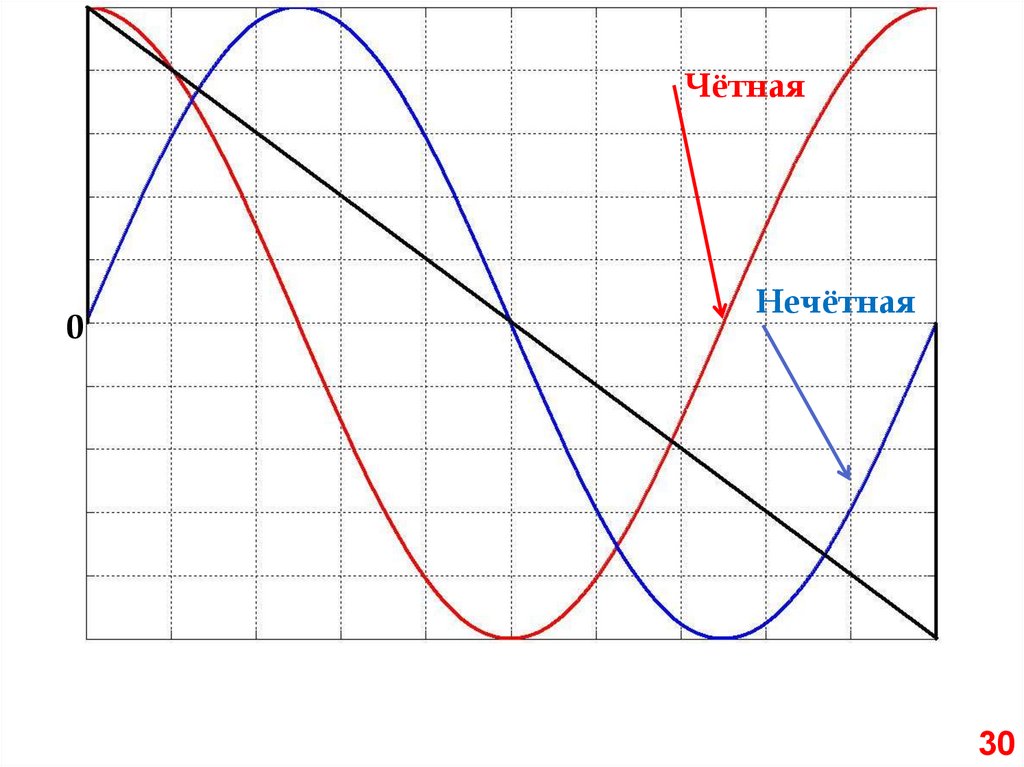
Чётная0
Нечётная
30
31.
.31
32.
TT
4U 0 2
2 2
sin ( n 0 t ) dt t sin ( n 0 t ) dt
bn
T
T
0
0
2
sin ax x cos ax
;
x
sin
ax
dx
.
2
Справка: 0 T
a
a
2 T
2 T
2 T
cos
n
sin
n
T
cos
n
4U 0
2
T 2 cos (0) 2
T 2
T 2
0
0
2
T
n 0
n 0
T
T 2
n 0
( n 0 )
№1
2
3
4
5
6
cos n
4U 0 cos n cos (0) 2 sin n
0
0 .
2
T
n 0
n 0
T ( n 0 )
n 0
Так как
0
2
, то третий член равен нулю, первый и пятый уничтожаются.
T
4U 0 1 4U 0 T 2U 0 1
bn
.
T n 0 T n 2
n
2U 0 sin(n 0 t )
U (t )
.
n 1
n
32
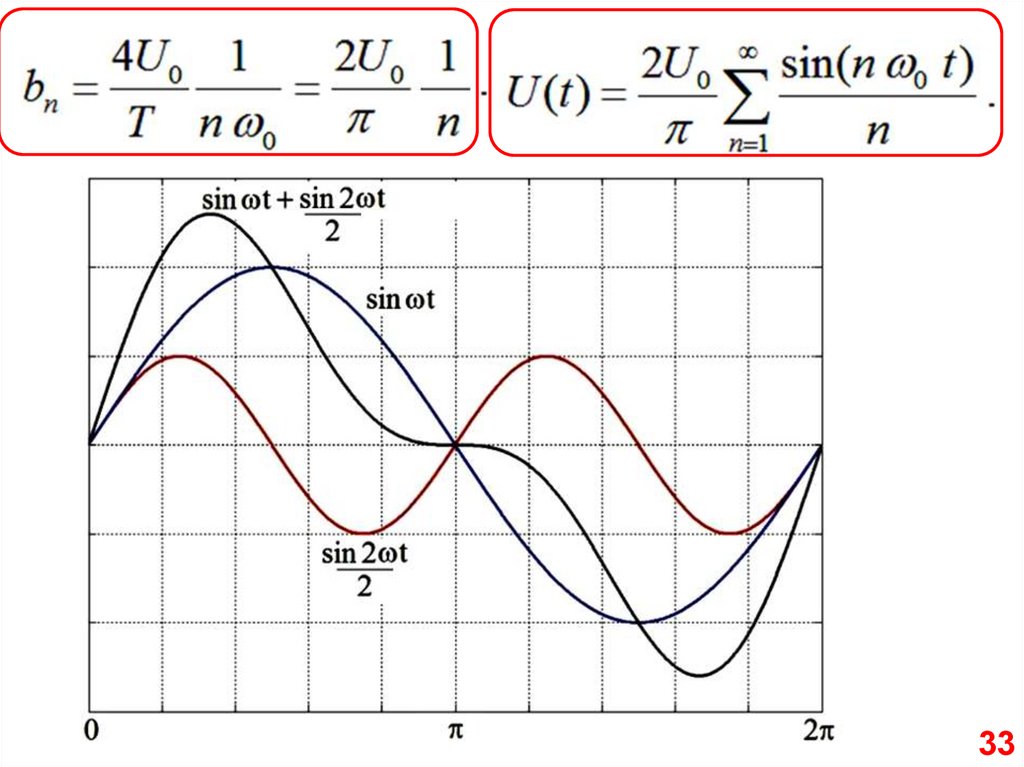
33.
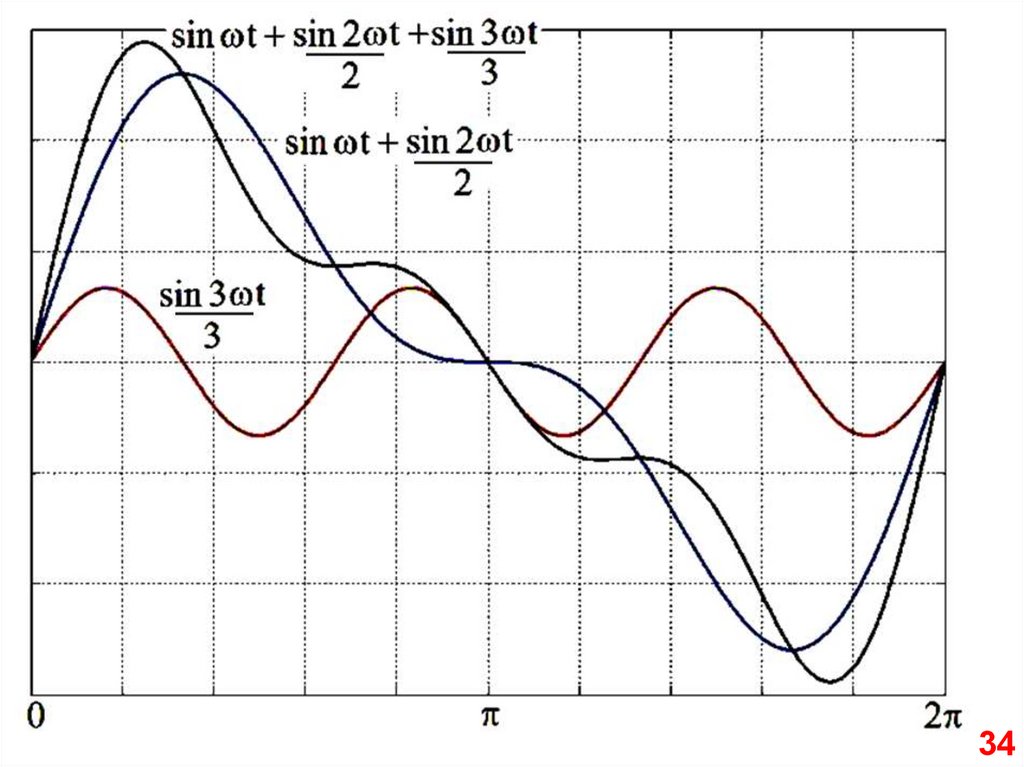
3334.
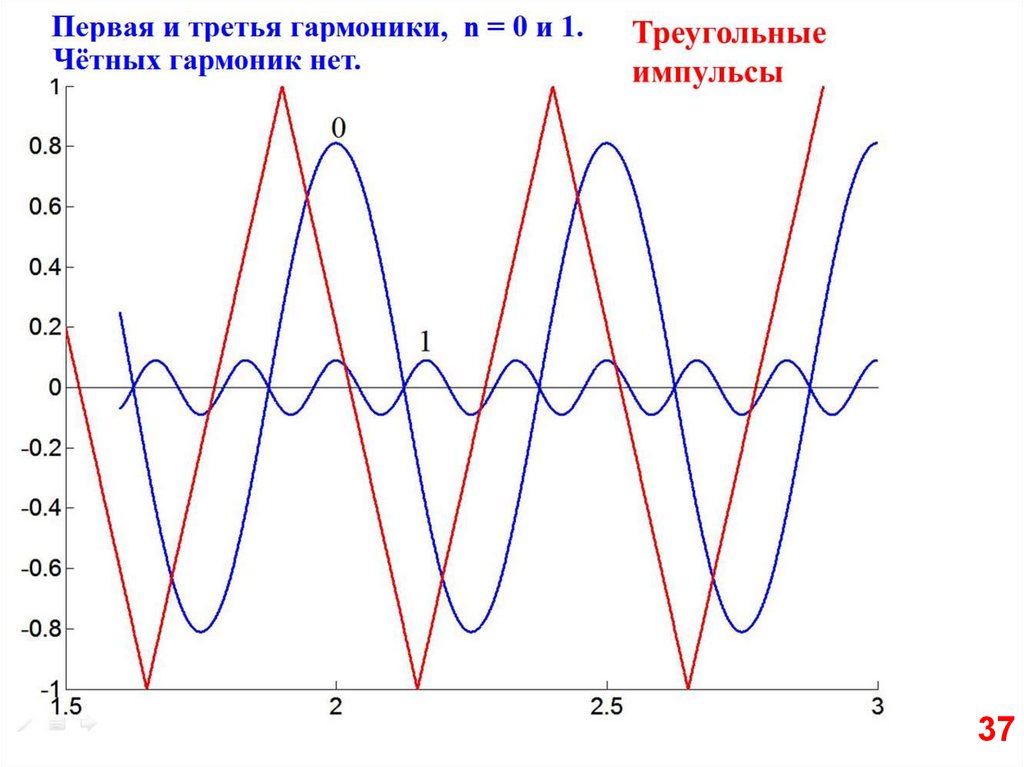
3435.
3536.
3637.
3738.
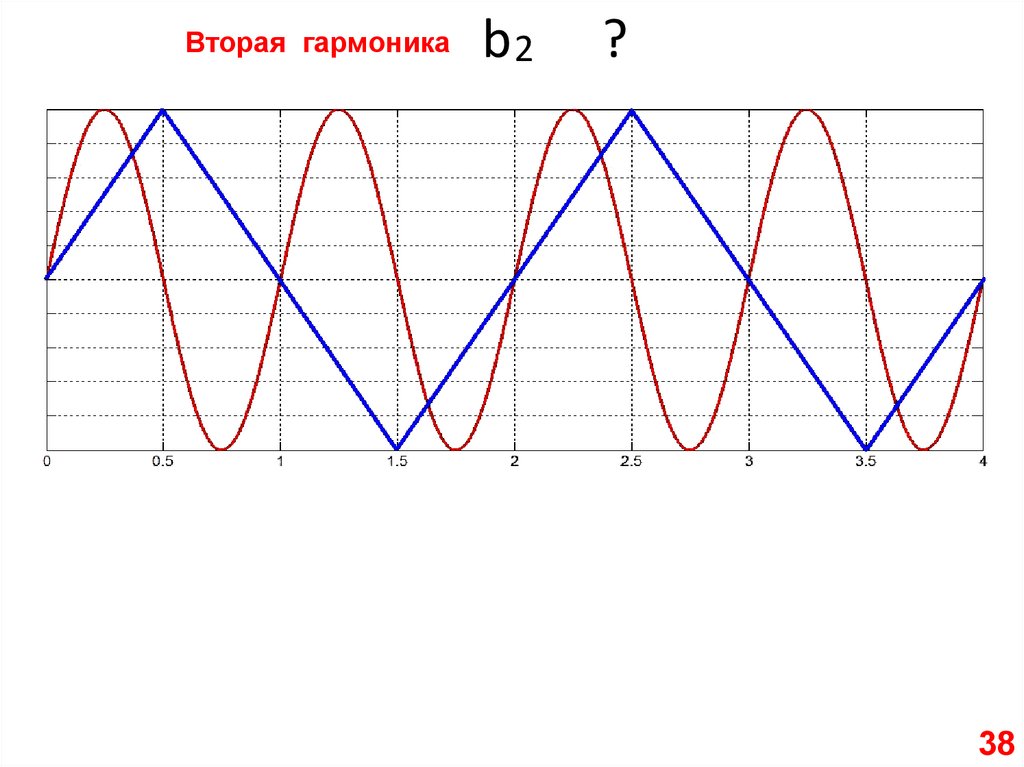
Вторая гармоникаb2
?
38
39.
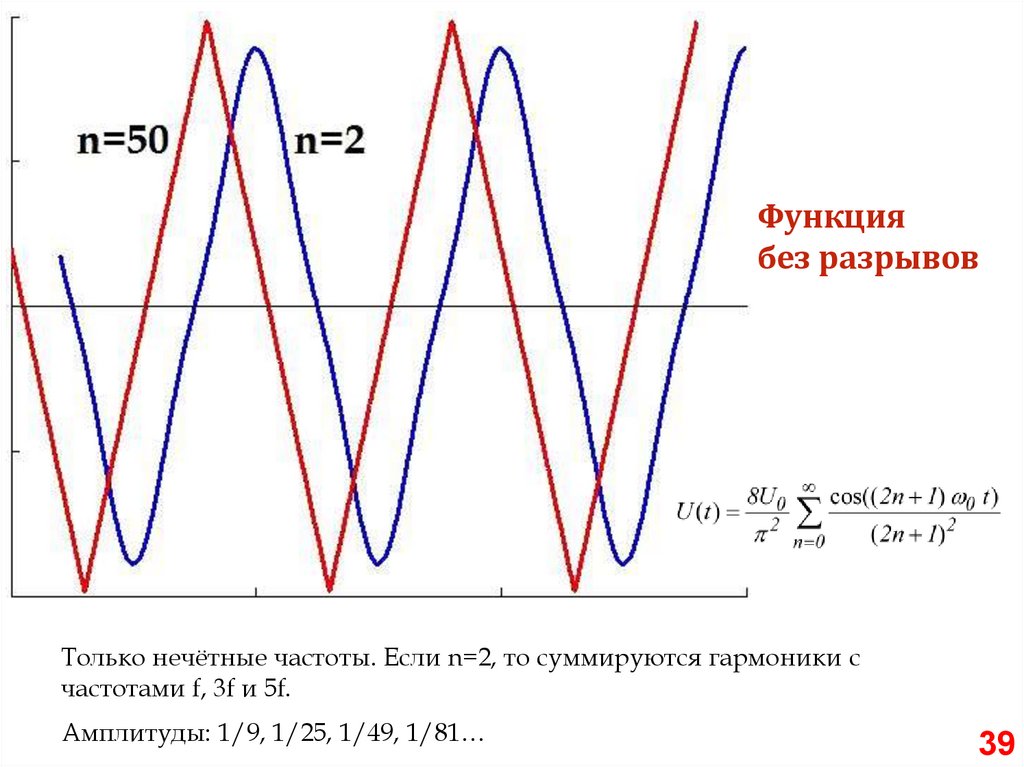
Функциябез разрывов
Только нечётные частоты. Если n=2, то суммируются гармоники с
частотами f, 3f и 5f.
Амплитуды: 1/9, 1/25, 1/49, 1/81…
39
40.
4041.
Остальные с k = m будут равны нулю!41
42.
4243.
4344.
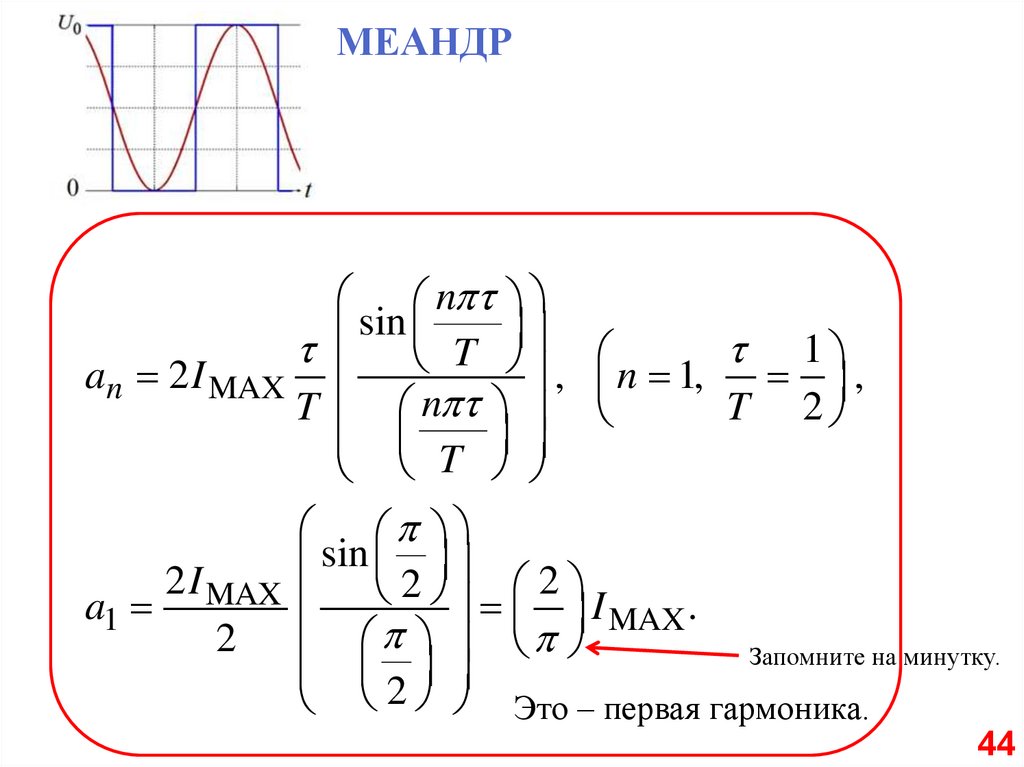
МЕАНДРn
sin
1
T
an 2 I MAX
, n 1,
,
T n
T 2
T
sin
2 I MAX
2
2
a1
I MAX .
2
Запомните на минутку.
2
Это – первая гармоника.
44
45.
4546.
4647.
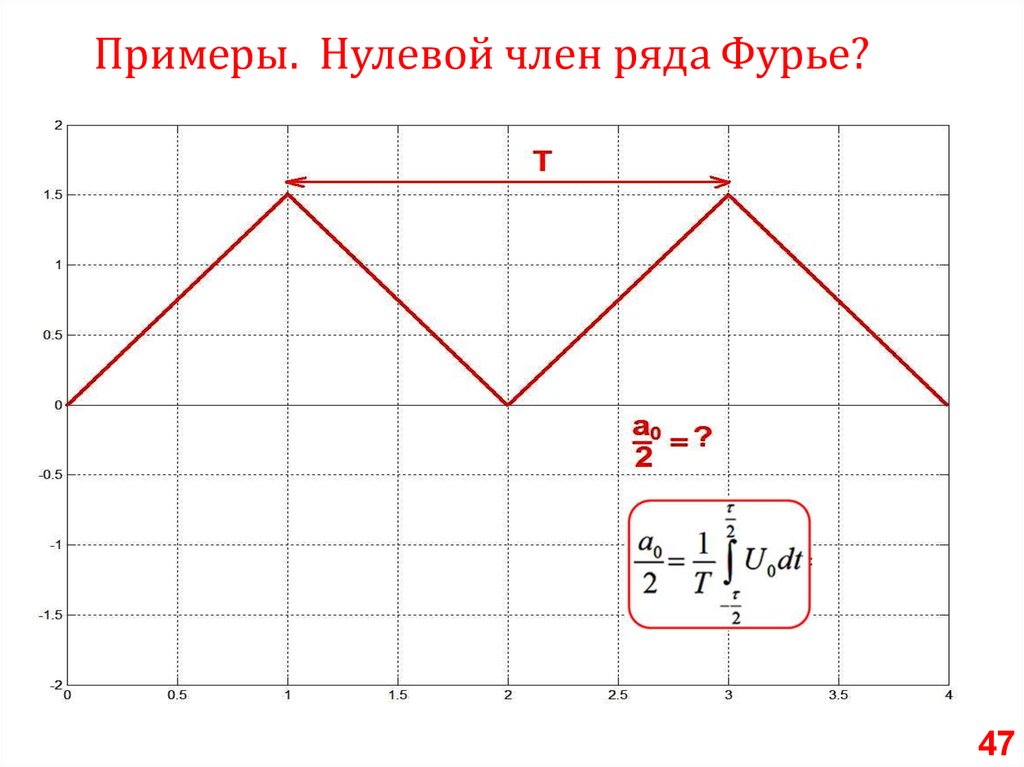
Примеры. Нулевой член ряда Фурье?47
48.
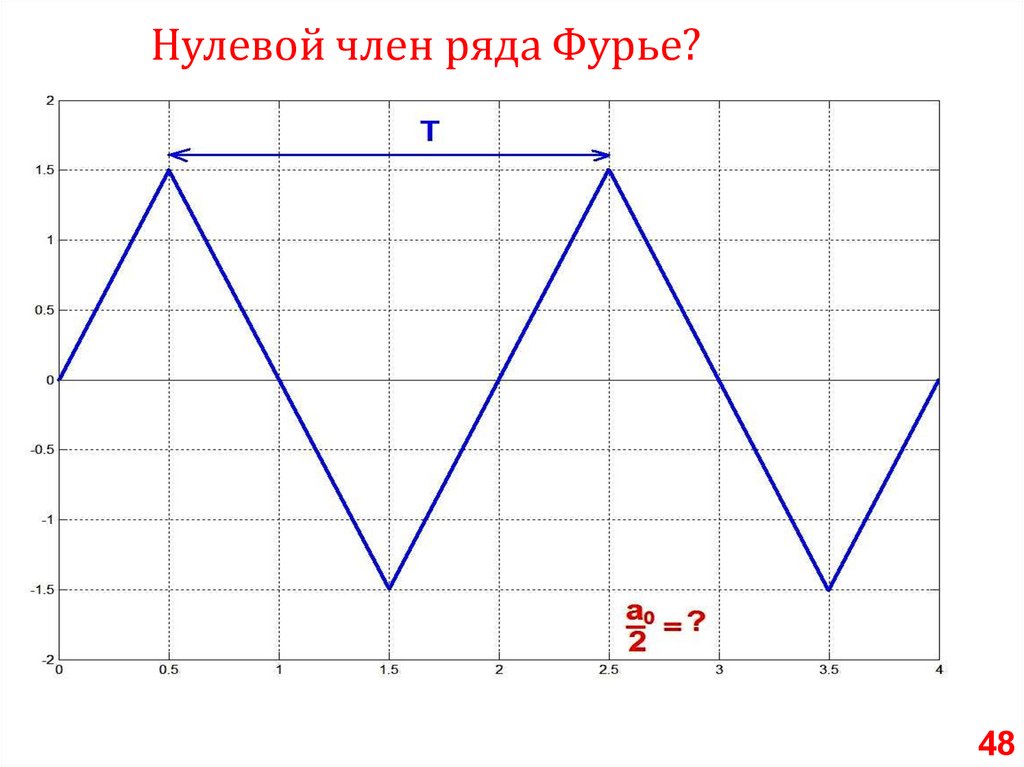
Нулевой член ряда Фурье?48
49.
4950.
5051.
ПреобразованиеФурье
Солнечный луч, разложенный на спектр, является физическим аналогом математических
преобразований .
Функция интенсивности от времени трансформировалась в функцию амплитуды в зависимости
от частоты.
Преобразование Фурье может представить сигнал, изменяющийся во времени,
в виде зависимости частоты и амплитуды, но оно даёт также информацию о фазе.
Анализ Фурье был вызовом математическим теориям, которых твёрдо придерживались его
современники. В начале XIX века многие выдающиеся парижские математики, в том числе такие как
Лагранж, Лаплас, Лежандр, Био и Пуассон, не могли принять утверждение Фурье о том, что любое
исходное распределение температуры можно разложить на составляющие в виде главной гармоники
и гармоник более высоких частот. Леонард Эйлер также считал идеи Фурье ошибочными, хотя к тому
времени сам пришёл к выводу, что некоторые функции можно представить суммой синусоид. И когда
Фурье огласил своё утверждение на одном из заседаний Французской академии наук, Лагранж заявил,
что это невозможно.
51
52.
Преобразование ФурьеF
F t e i t dt F t cos t i sin t dt ,
1
i t
F t
F e
d .
2
Бывает и так, но мы против!
F
1
i t
F
t
e
dt ,
2
1
i t
F t
F
e
d .
2
52
53.
5354.
Производная54
55.
Масштаб времениСдвиг времени
Энергия сигнала
Перенос спектра
55
56.
5657.
Рассмотрим теорему о переносе спектра:F (t ) f (t ) cos 0t ,
F ( ) F (t ) e
i t
f (t )
e
i 0t
e
2
dt
i 0t
e
i t
dt
1
1
i ( 0 ) t
i ( 0 ) t
f (t ) e
dt f (t ) e
dt
2
2
f ( 0 ) f ( 0 )
.
2
2
57
58.
5859.
5960.
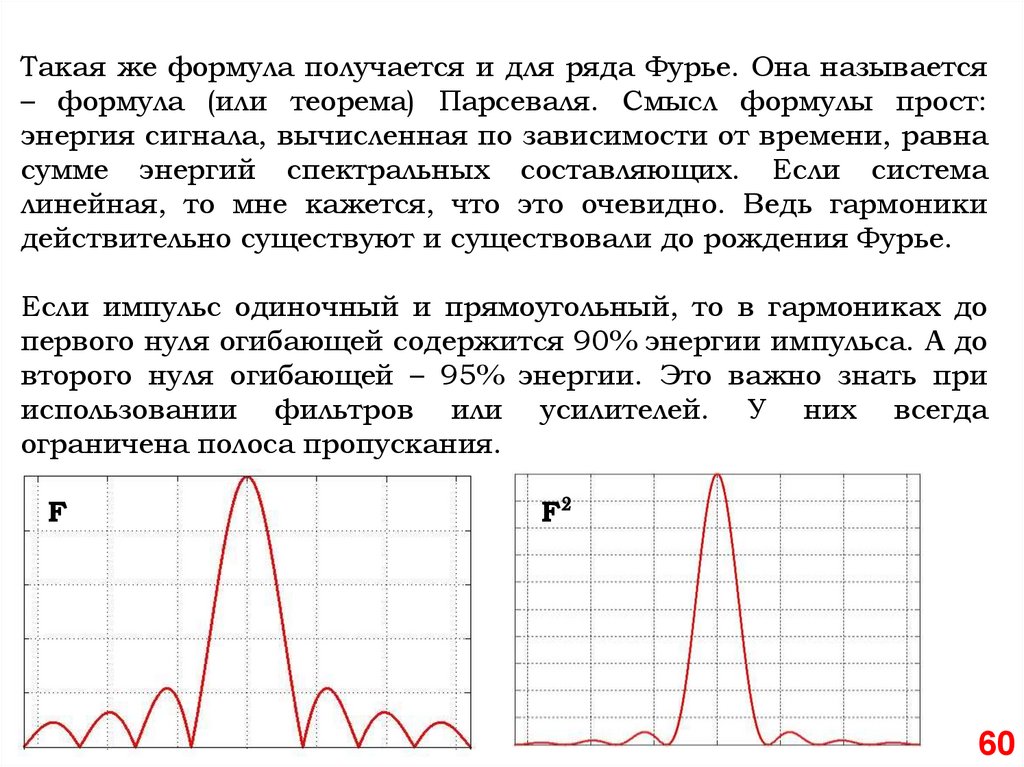
Такая же формула получается и для ряда Фурье. Она называется– формула (или теорема) Парсеваля. Смысл формулы прост:
энергия сигнала, вычисленная по зависимости от времени, равна
сумме энергий спектральных составляющих. Если система
линейная, то мне кажется, что это очевидно. Ведь гармоники
действительно существуют и существовали до рождения Фурье.
Если импульс одиночный и прямоугольный, то в гармониках до
первого нуля огибающей содержится 90% энергии импульса. А до
второго нуля огибающей – 95% энергии. Это важно знать при
использовании фильтров или усилителей. У них всегда
ограничена полоса пропускания.
F
F2
60
61.
6162.
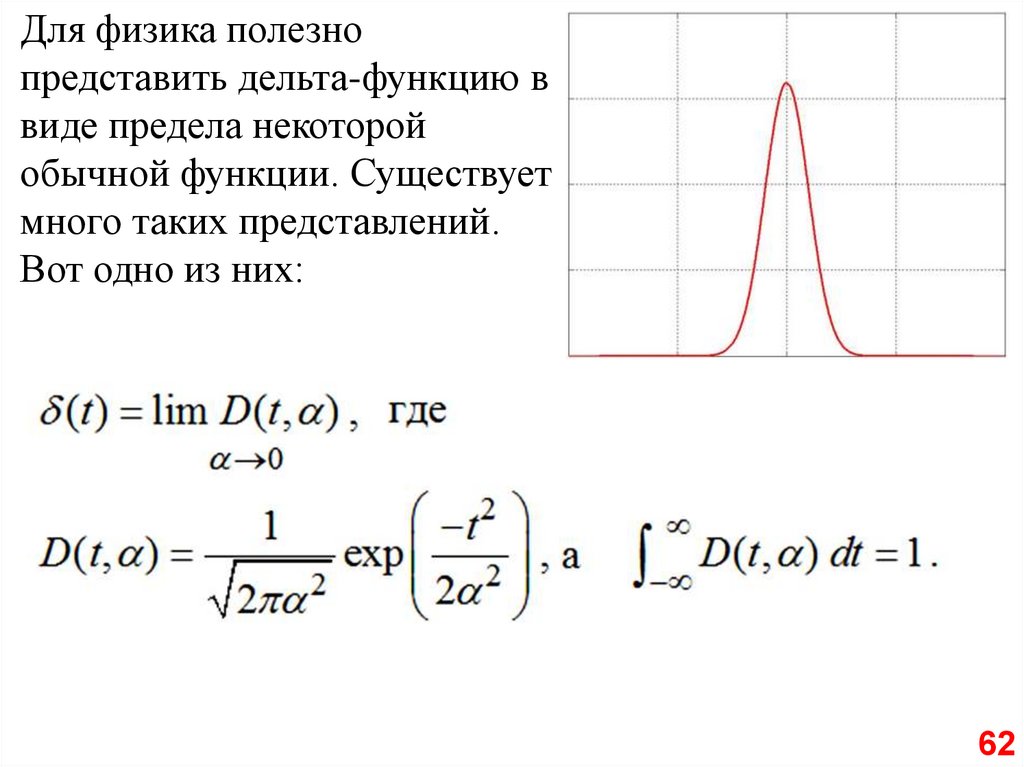
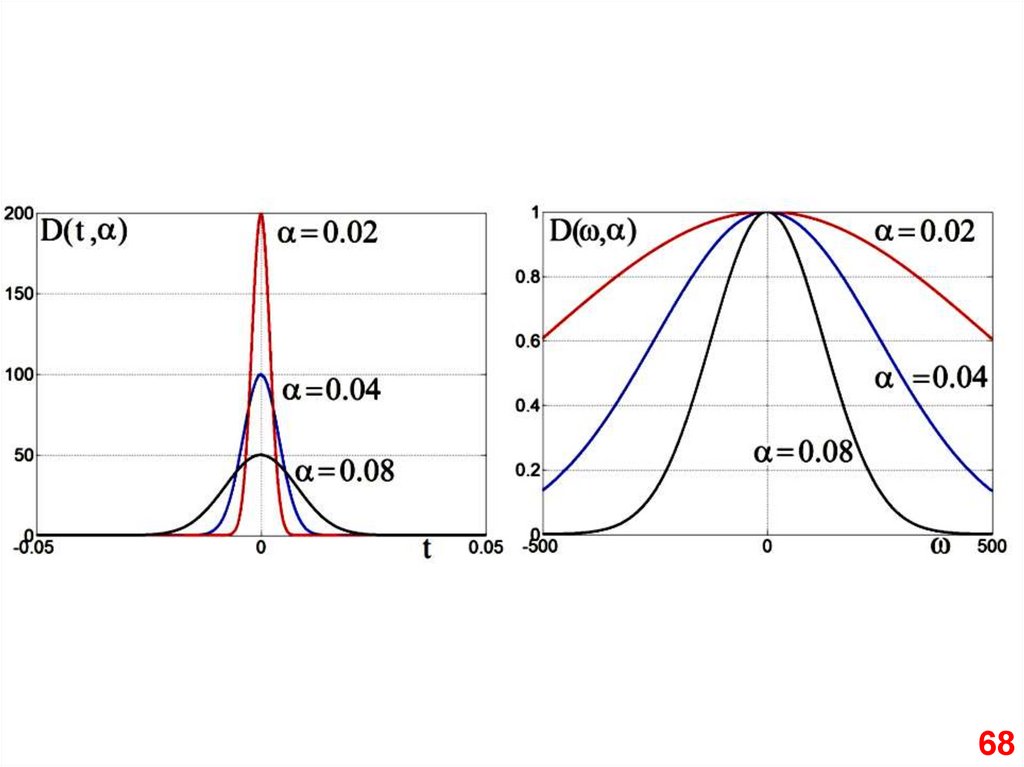
Для физика полезнопредставить дельта-функцию в
виде предела некоторой
обычной функции. Существует
много таких представлений.
Вот одно из них:
62
63.
6364.
Показательстепени
экспоненты
Заменим
переменную
64
65.
6566.
6667.
6768.
6869.
6970.
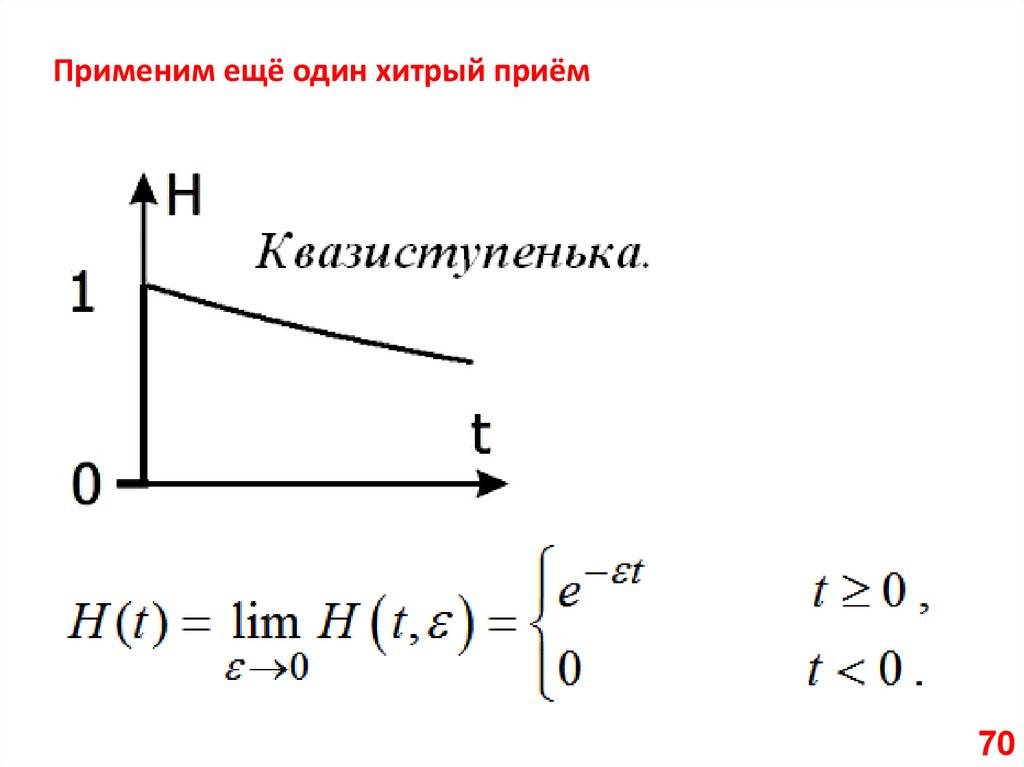
Применим ещё один хитрый приём70
71.
( i ) te
1
t i t
H ( , ) e
dt
0
.
i
i
0
0
1 1 i 1
H ( ) lim
e
0 i i
i
2.
Отсюда модуль спектральной плотности
ступеньки будет
а аргумент: ( )
t
H (t ) (t ) dt ,
2
1 ,
H ( )
.
dH (t )
(t ) .
dt
Запомните!
71
72.
The END73.
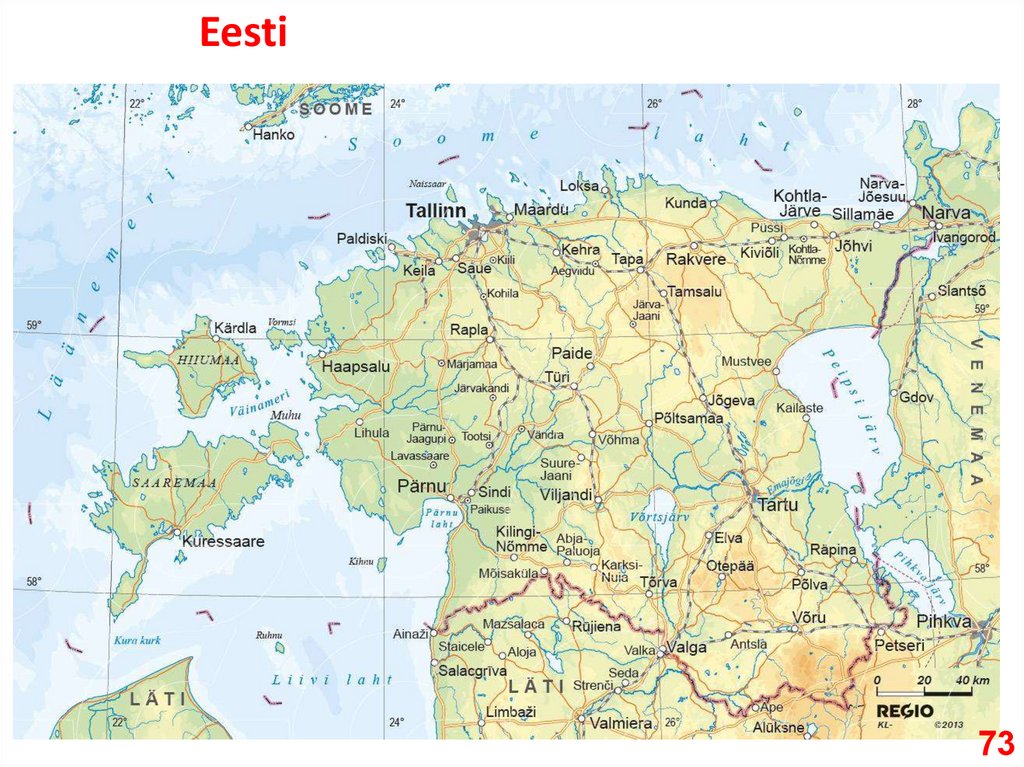
Eesti73
74.
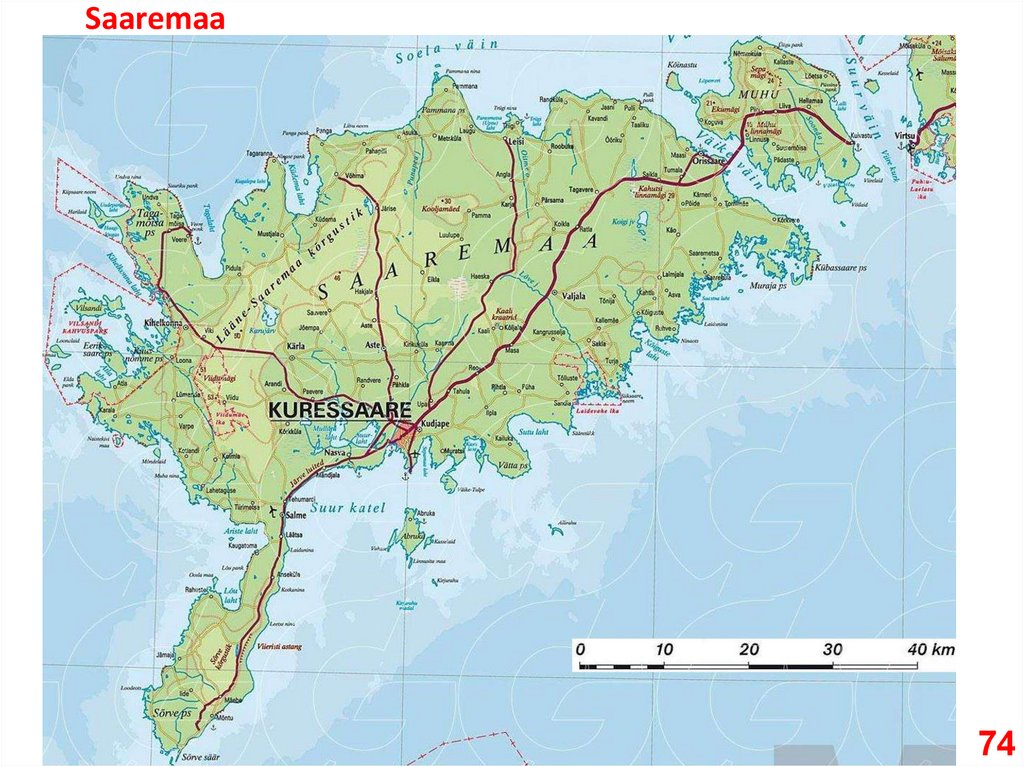
Saaremaa74
75.
Suur Tŏll ja Pirit75
76.
Kaali kraater76











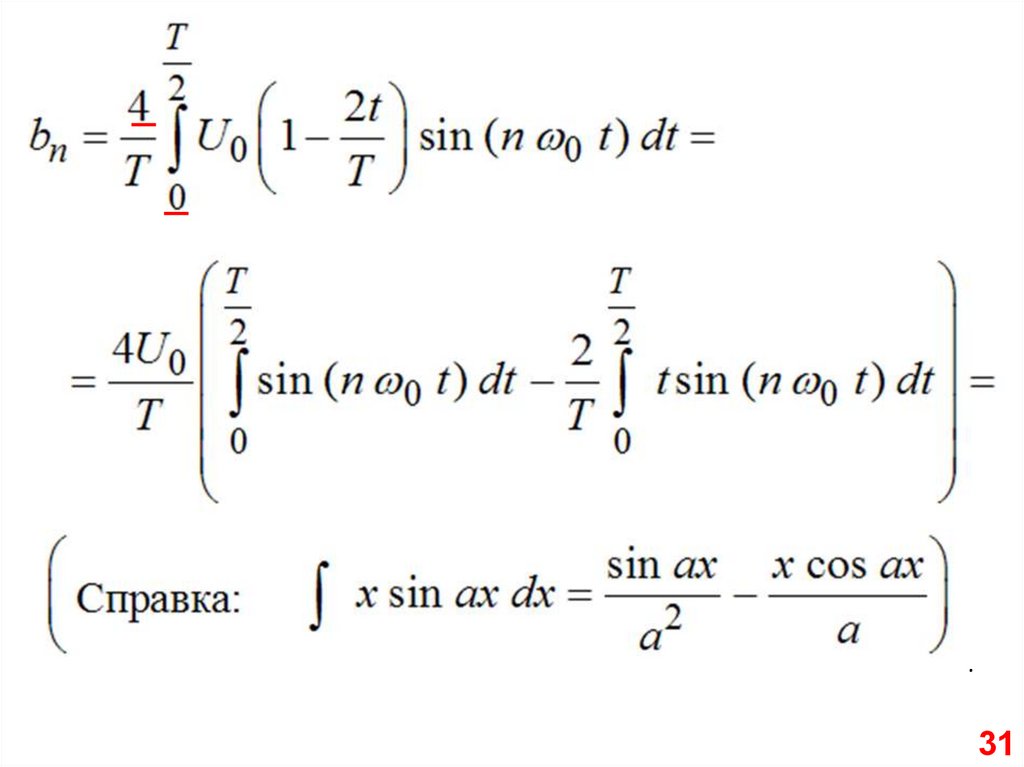
































 Электроника
Электроника








