Похожие презентации:
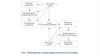
Иерархия построения радиотехнической системы
1. Иерархия построения радиотехнической системы
2.
Слайд 1-13.
Слайд 1-24.
Слайд 1-35.
Слайд 1-46.
Слайд 1-57.
Слайд 1-68.
9.
Слайд 2-110.
Слайд 2-211.
Слайд 2-312.
Слайд 2-413.
Слайд 2-514.
15.
16.
Слайд 3-1Спектральный анализ сигналов
1. Непрерывное преобразование Фурье
Спектральное представление сигналов основано на разложении функций в ряд.
0
t
T
Рис.1. Непрерывная периодически повторяющаяся функция (сигнал) U(t).
Периодически повторяющаяся функция U(t) (далее - сигнал) любой формы с периодом повторения T на бесконечном интервале
времени может быть представлена бесконечной суммой элементарных тригонометрических функций с надлежащим образом подобранными
параметрами: амплитудой Ak и начальной фазой φk:
или в форме:
a
U (t ) 0 A cos(k t )
1
k
2 k 1 k
a
U (t ) 0 (ak cos(k 1t ) bk sin( k 1t ))
2 k 1
(1)
(2)
Преобразование выражения (1) в форму (2) основано на представлении гармонического колебания в виде двух квадратурных
составляющих: косинусной и синусной с нулевыми начальными фазами.
Это разложение (1) или (2) периодической функции (сигнала) в бесконечный ряд тригонометрических функций называется рядом
Фурье, а функции ряда называются гармониками.
Частоты гармоник кратны основной частоте ω1:
1 2
T
f1 1
T
- круговая частота (рад/сек)
- циклическая частота (герц)
17.
Слайд 3-2Коэффициенты (амплитуды гармоник) ряда (2) могут быть вычислены:
T
2 2
a
U (t )dt
0 T T
2
T
2 2
a U (t ) cos(k t )dt
k TT
1
(3)
2
T
2 2
b U (t ) sin( k t )dt
k TT
1
2
Амплитуды Ak и фаза φk гармоники ряда (1) связаны с коэффициентами ak и bk ряда (2) связаны соотношениями:
b
arctg k
k
a
k
A a 2 b2
k
k
k
Ряд Фурье обычно принято представлять в комплексной форме.
Для преобразования выражения (2) в комплексную форму следует воспользоваться формулами Эйлера (представление
тригонометрических функций экспоненциальными):
e j e j
cos( )
2
e j e j
sin( )
2j
Тогда разложение U(t) в ряд может быть представлено:
a
U (t ) 0 (a
2 k 1 k
e
jk t
jk t
1 e
1
2
j b
k
e
jk t
jk t
1 e
1
)
2
или в форме:
a
a jbk jk t
a jbk jk t
1 k
1
U (t ) 0 k
e
e
2 k 1
2
2
k 1
(4)
18.
Слайд 3-3Обозначим коэффициенты ряда (4)
a jb
k
C k
k
2
C
a jb
k
k
k
2
С учетом соотношений (3) коэффициенты Ck и C-k вычисляются:
T
a jb
2
1
k
C k
U (t )(cos(k t ) j sin( k t )dt
1
k
1
2
T T
2
T
a jb
2
1
k
C k
U (t )(cos(k t ) j sin( k t )dt
1
k
1
2
T T
2
(5)
±jα
Так как
cos(α) ± jsin(α) = e
то соотношения (5) в комплексной форме будут иметь вид
jk t
1 2
1 dt
C
U (t )e
k
T T
T
2
jk t
1 2
1 dt
U
(
t
)
e
T T
T
C
k
2
Легко заметить, что значения C-k отличаются от Ck лишь знаком показателя экспоненты.
Если ввести отрицательные значения k и учесть, что
a0
C0
2
то разложение в ряд U(t) (4) можно представить в следующей форме:
jk t
jk t
jk t
1 C e
1
1
U (t ) C e
C e
k
k
k
k 0
k 1
k
19.
Слайд 3-4И окончательно запишем формулы преобразования Фурье для периодически повторяющихся сигналов с периодом повторения T:
jk t
1 2
1 dt
C
U
(
t
)
e
k T T
T
- прямое преобразование Фурье
(6)
- обратное преобразование Фурье
(7)
2
U (t )
k
C e
k
jk t
1
где Сk комплексные гармоники – спектр периодически повторяющегося сигнала.
Еще раз обратим внимание на свойства спектра периодически повторяющегося сигнала на бесконечном интервале времени:
- спектр является дискретным;
- гармоники спектра кратны основной частоте f = 1/T (ω = 2π/T);
- число гармоник бесконечно;
- математически спектр содержит как реальные – положительные по частоте гармоники, так и отрицательные гармоники (k –
отрицательные значения).
Спектр (а точнее спектральная плотность) не периодического, одиночного, сигнала может быть получен путем предельного перехода
при T
2
1
d 0
T
k
1
C S ( j )
k
- интервал между соседними гармониками
ω - непрерывная частота
- спектральная плотность
и преобразование Фурье для одиночного сигнала выполняется п
S ( j ) U (t )e
j t
dt
(8)
20.
Слайд 3-6Огибающая дискретного спектра периодического сигнала полностью совпадает со спектральной плотностью одиночного сигнала.
Поэтому для получения спектра периодического сигнала с периодом T достаточно по (8) вычислить спектральную плотность для
одиночного сигнала и взять дискретные его значения через f = 1/T.
U (t )
1
j t
d
S ( j )e
2
(9)
Пример:
Спектральная плотность прямоугольного импульса длительностью τ и амплитудой Um
2
S ( j ) U e
m
j t
2
dt U m e
2
j t
U
dt m e j t
j
2
Пределы
интегрирования
2
2
После подстановки пределов интегрирования и с учетом формул Эйлера получим
S ( j )
2 U
j
m e
2 e
2j
j
2
U m
sin(
)
2
2
1
2
sin
0.5
2
0
Рис.2. Модуль функции sin(x)/x (амплитудный спектр прямоугольного импульса)
21.
Слайд 3-71
2
sin
0.5
2
0
Рис.2. Модуль функции sin(x)/x (амплитудный спектр прямоугольного импульса)
Как следует из приведенного графика, функция sin(x)/x имеет лепестковый характер и принимает значения, равные 0 при x = 2nπ n = 1, 2,
3…
или для спектра при значениях частоты f = 1/τ, 2/τ, 3/τ…
Уровень лепестков относительно главного составляет:
- первый - 0.217
- второй - 0.13
- третий - 0.09
- четвертый – 0.07
т.е., хотя в главном лепестке спектра и сосредоточена основная мощность прямоугольного импульса (более 90%), все же спектр
(спектральная плотность) его достаточно медленно убывает с частотой.






















 Электроника
Электроника