Поверхности второго порядка

1. Поверхности 2-го порядка

.

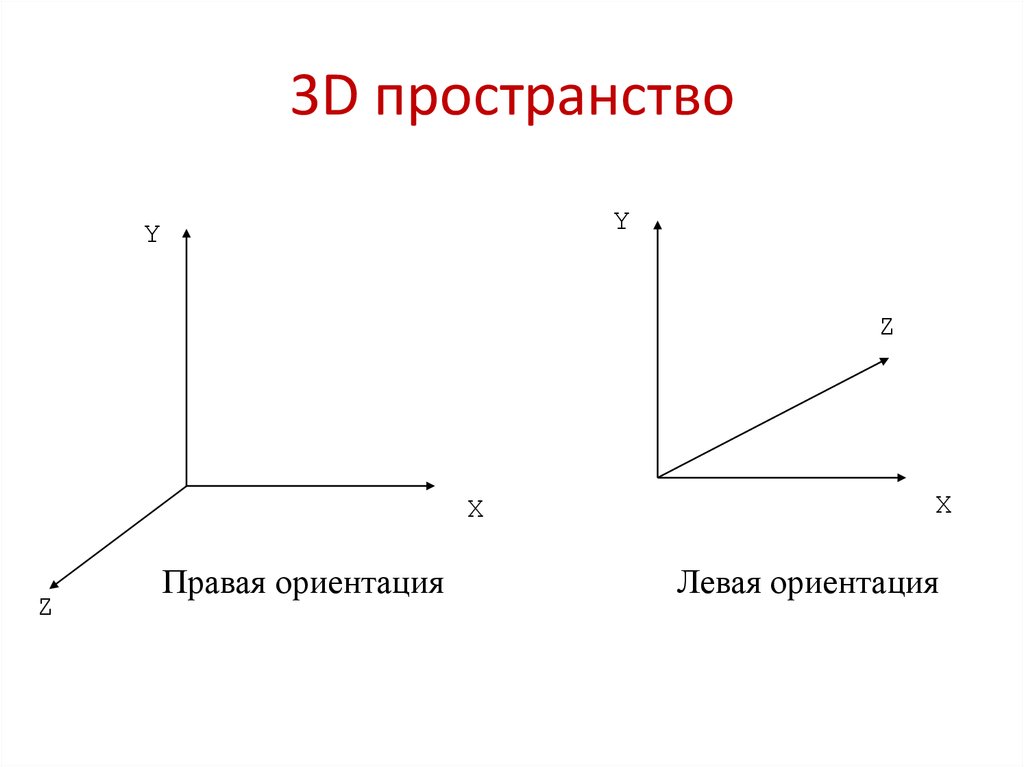
2. 3D пространство

Y
Y
Z
X
Z
Правая ориентация
X
Левая ориентация

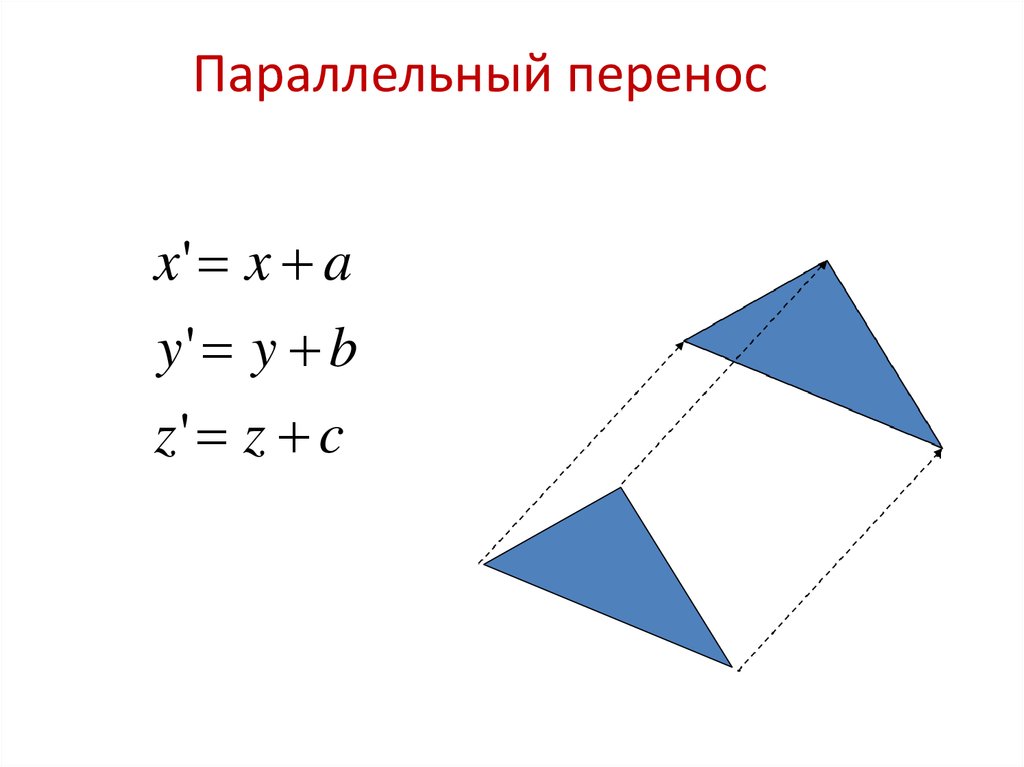
3. Параллельный перенос

x' x a
y' y b
z' z c

4. Параллельный перенос

x' x a
y' y b
z' z c
x' 1
y' 0
z' 0
1 0
0 0 a x
1 0 b y
0 1 c
z
0 0 1 1

5. 3D поворот

Рассматривается поворот осей координат вокруг
начала координат.
В матричном представлении: всякая ортогональная
3х3 матрица задает поворот:
– Строки и столбцы образуют ортонормированную
систему
– Определитель равен +1 или -1
– Обратная матрица совпадает с транспонированной.

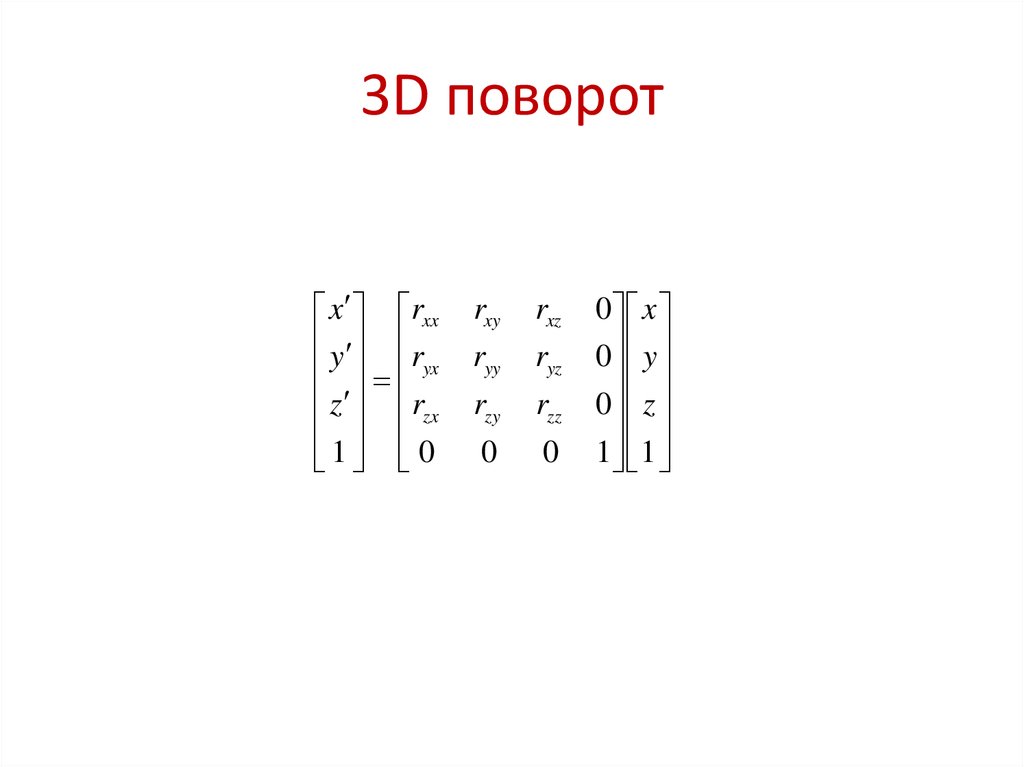
6. 3D поворот

x rxx
y r
yx
z rzx
1 0
rxy
ryy
rxz
ryz
rzy
0
rzz
0
0 x
0 y
0 z
1 1

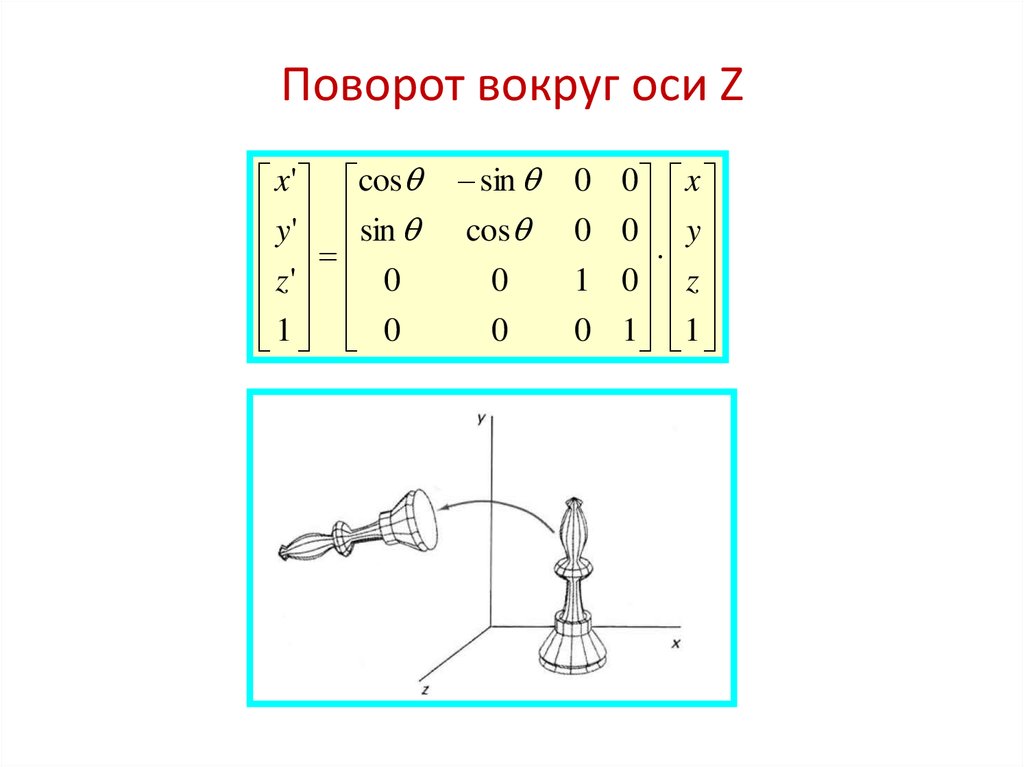
7. Поворот вокруг оси Z

x' cos
y ' sin
z' 0
1 0
sin
cos
0
0
0 0 x
0 0 y
1 0 z
0 1 1

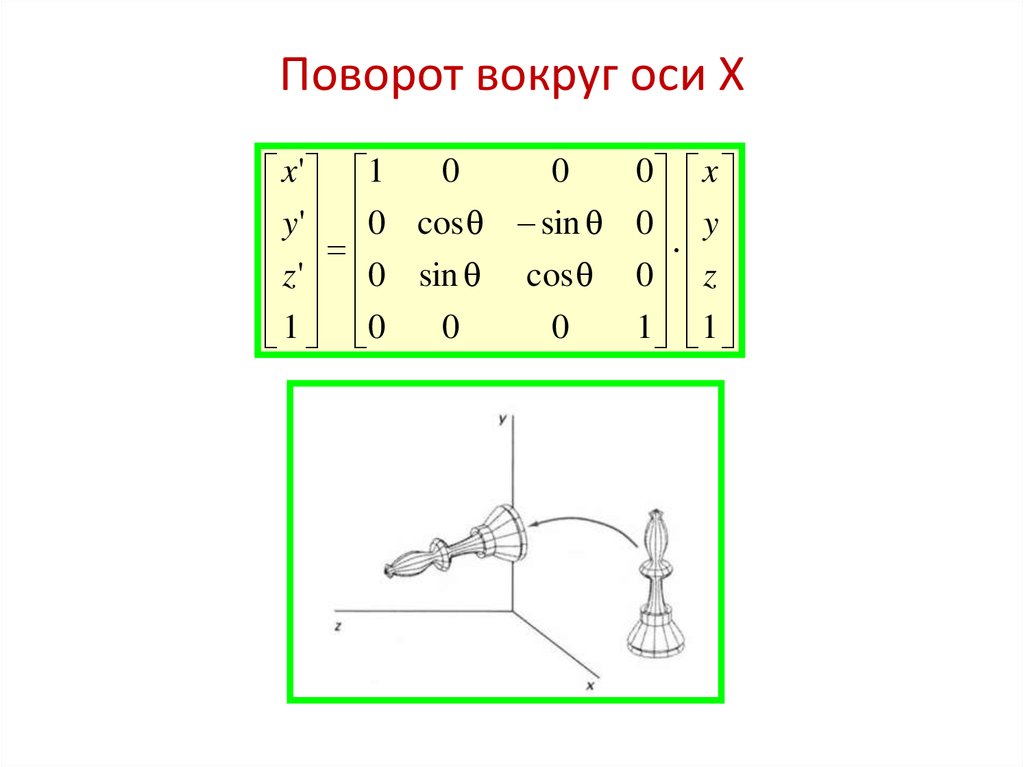
8. Поворот вокруг оси X

0
0
x' 1
y ' 0 cos sin
z ' 0 sin cos
0
0
1 0
0 x
0 y
0 z
1 1

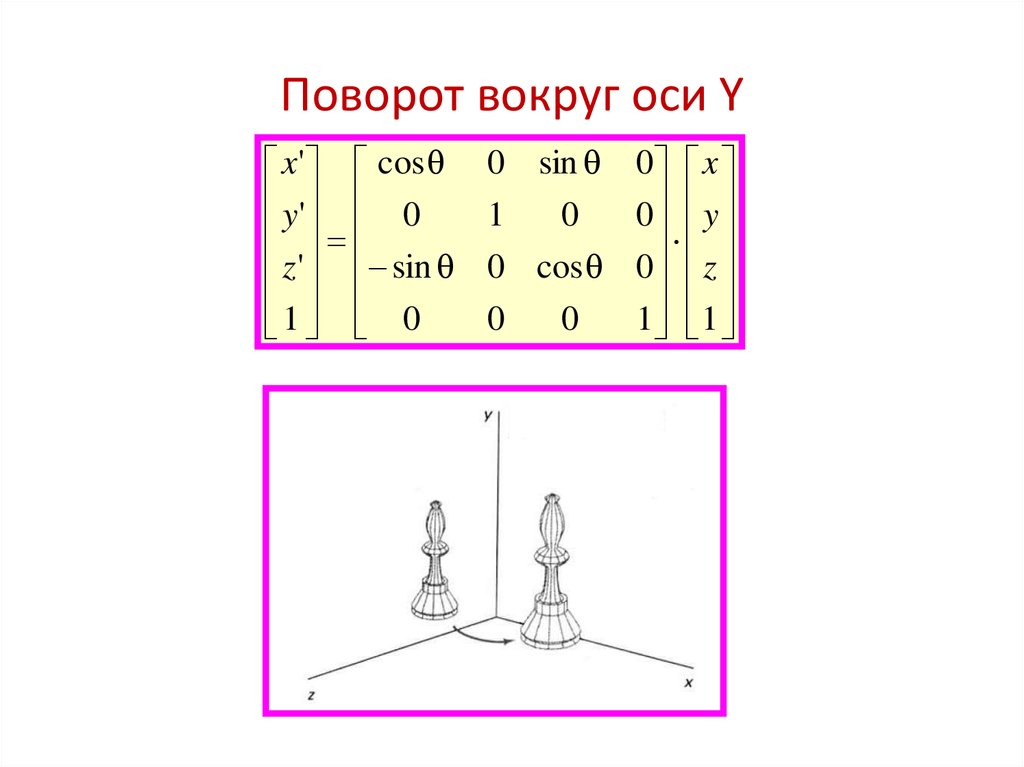
9. Поворот вокруг оси Y

x' cos
y ' 0
z ' sin
1 0
0 sin 0 x
1
0
0 y
0 cos 0 z
0
0
1 1

10. Уравнение поверхности 2-го порядка

Уравнение поверхности 2-го порядка
главная(квадратичная) часть
.
линейная часть
Основная задача состоит в умении по уравнению определить тип
поверхности, привести само уравнение к каноническому виду и
построить поверхность в системе координат. Сначала произведем
поворот системы координат.

11.

Составим матрицу
Так как матрица симметрическая, то существует
ортогональное преобразование (поворот),
приводящее главную часть
к главным осям, так что преобразованное уравнение имеет
вид
Хотя бы один из коэффициентов при квадратах отличен от
нуля, иначе матрица A была бы нулевой. Рассмотрим три
случая.

12. 1. Все собственные числа отличны от нуля.

1 x 2 2 y 2 3 z 2 2b1 x 2b2 y 2b3 z c 0
Выделим полные квадраты
1 ( x
b1
1
) 2 ( y
2
b2
2
) 3 ( z
2
выполним параллельный перенос
получим
2
2
2
1 ( x ) 2 ( y ) 3 ( z ) c 0
b3
3
) 2 c 0
x x
y y
z z
b1
1
b2
2
b3
3

13. 1. Все собственные числа отличны от нуля.

1 x 2 2 y 2 3 z 2 c 0
1.1. Если знаки 1 , 2 , 3 одинаковы и с=0, преобразуем
уравнение
x2
y2
z2
0
1
1
1
1
2
3
Получим каноническое уравнение точки (вырожденный
эллипсоид)
x2 y2 z 2
2 2 0
2
a
b
c

14. 1. Все собственные числа отличны от нуля.

1 x 2 2 y 2 3 z 2 c 0
1.2. Если знаки 1 , 2 , 3 и с одинаковы, то действительных
решений нет, преобразуем уравнение
x2
y2
z2
1
с
с
с
1
2
3
Получим каноническое уравнение мнимого эллипсоида
x2 y2 z 2
2 2 1
2
a
b
c

15. 1. Все собственные числа отличны от нуля.

1 x 2 2 y 2 3 z 2 c 0
1.3. Если знаки 1 , 2 , 3 , с одной стороны, и с различны,
то действительных решений нет, преобразуем уравнение
x2
с
1
y2
с
2
z2
с
1
3
Получим каноническое уравнение действительного
эллипсоида
x2 y2 z 2
2 2 1
2
a
b
c

16. Эллипсоид

Каноническое уравнение трехосного эллипсоида имеет вид
x2 y2 z 2
2 2 1
2
a
b
c
a, b, c
c
полуоси эллипсоида.
Центр этого эллипсоида находится
в начале координат.
Признаки уравнения эллипсоида:
1. Наличие квадратов всех трех переменных
2. Одинаковые знаки при квадратах переменных
a
b

17. 1. Все собственные числа отличны от нуля.

1 x 2 2 y 2 3 z 2 c 0
1.4. Знаки 1 , 2 , 3 различны, пусть знаки 1 , 2 0
отличаются от знака 3
и с =0, преобразуем уравнение
x2
y2
z2
1
1
1
1
2
0
3
Получим каноническое уравнение конуса
x2 y2 z 2
2 2 0
2
a
b
c

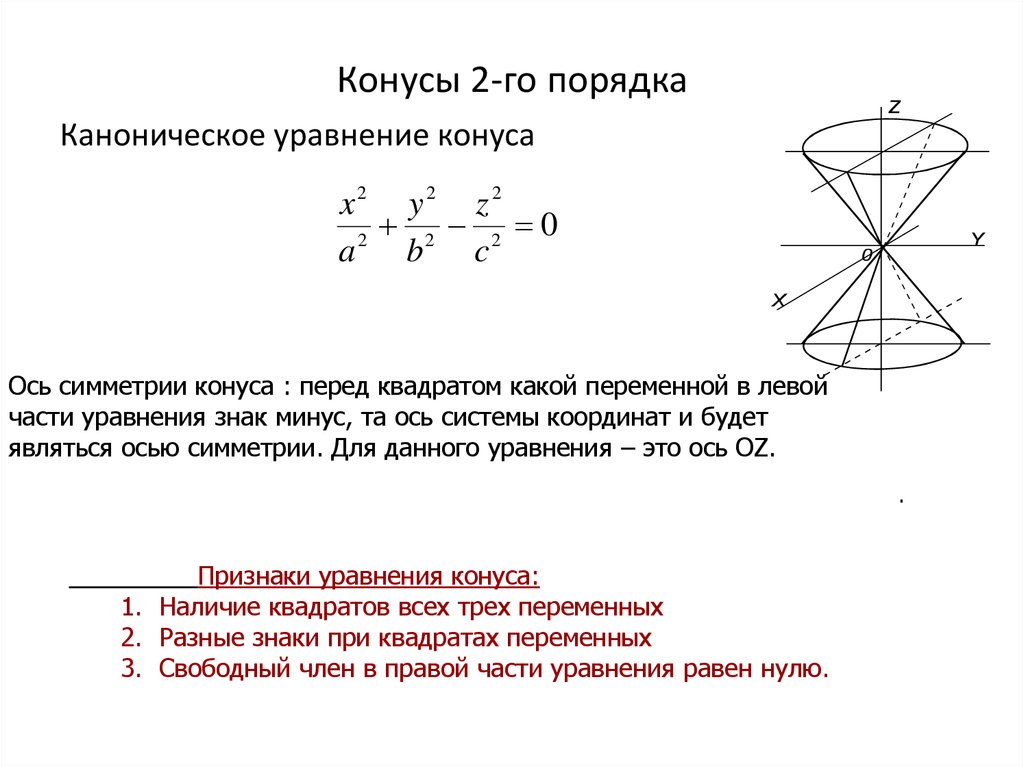
18. Конусы 2-го порядка

Каноническое уравнение конуса
x2 y2 z 2
2 2 0
2
a
b
c
Ось симметрии конуса : перед квадратом какой переменной в левой
части уравнения знак минус, та ось системы координат и будет
являться осью симметрии. Для данного уравнения – это ось OZ.
Признаки уравнения конуса:
1. Наличие квадратов всех трех переменных
2. Разные знаки при квадратах переменных
3. Свободный член в правой части уравнения равен нулю.

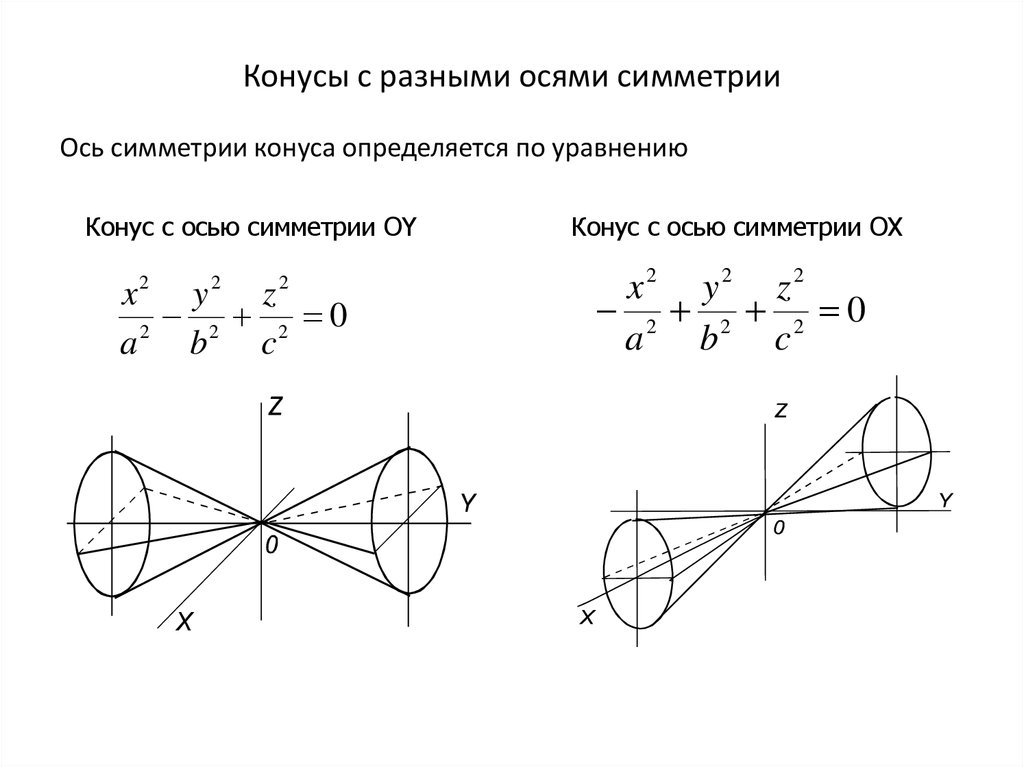
19. Конусы с разными осями симметрии

Ось симметрии конуса определяется по уравнению
Конус с осью симметрии OY
2
2
2
x
y
z
2 2 0
2
a b
c
Конус с осью симметрии OX
x2 y2 z 2
2 2 2 0
a
b
c

20. 1. Все собственные числа отличны от нуля.

1 x 2 2 y 2 3 z 2 c 0
1.5. Знаки 1 , 2 , 3 различны, пусть знаки 1 , 2 0
отличаются от знака 3
и с 0 , преобразуем
уравнение
x2
y2
z2
с
с
с
1
2
1
3
Получим каноническое уравнение гиперболоида
x2 y2 z 2
2 2 1
2
a
b
c

21. Гиперболоиды

Канонические уравнения гиперболоидов
x2 y2 z 2
2 2 1
2
a
b
c
В зависимости от знака перед единицей в правой
части гиперболоиды делятся на одно и двуполостные.
Каноническое уравнение однополостного
гиперболоида
a
b
x2 y2 z 2
2 2 1
2
a
b
c
a, b, c полуоси
1.
2.
3.
в
Признаки уравнения однополостного гиперболоида:
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Один знак минус при квадрате переменной в левой части уравнения,
правой части плюс 1.

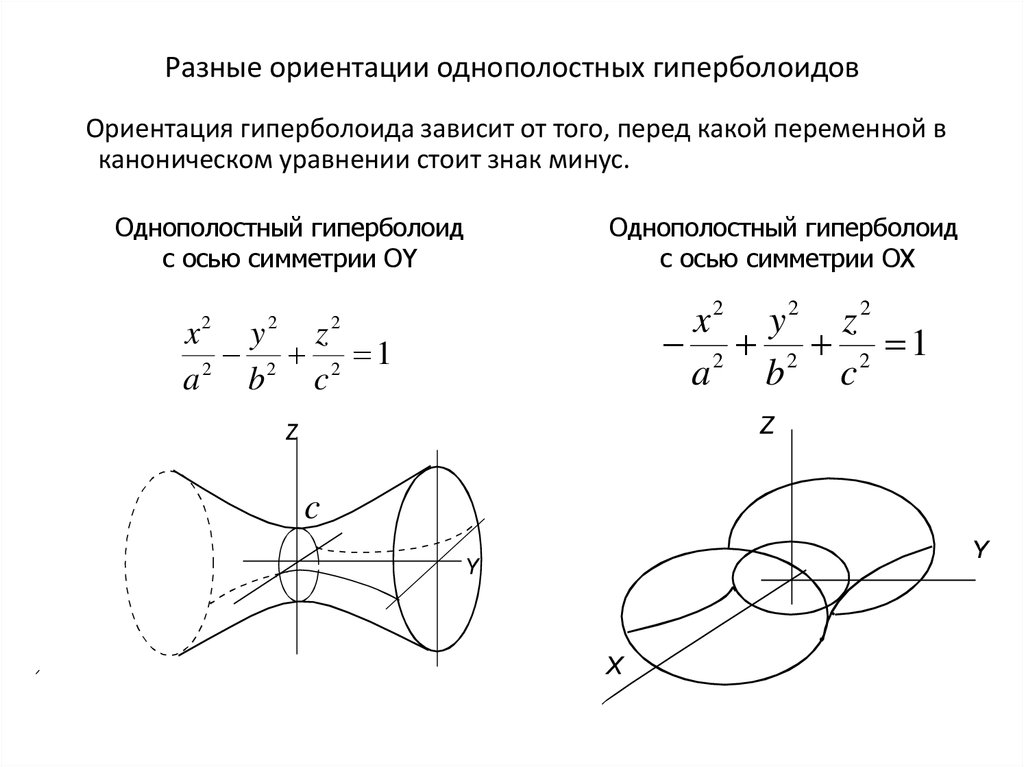
22. Разные ориентации однополостных гиперболоидов

Ориентация гиперболоида зависит от того, перед какой переменной в
каноническом уравнении стоит знак минус.
Однополостный гиперболоид
с осью симметрии OY
2
2
2
x
y
z
2 2 1
2
a b c
c
Однополостный гиперболоид
с осью симметрии OX
x2 y2 z 2
2 2 2 1
a b c

23. Гиперболоиды

Каноническое уравнение двуполостного гиперболоида
x2 y2 z 2
2 2 1
2
a
b
c
a, b, c
полуоси
Если из уравнения выразить z, то получим
Т.к.
x2 y2
z c
2 1
2
a
b
2
2
x
y
1 1 , то получается, что | z | c
2
2
a
b
c
c
Двуполостный гиперболоид на проходит через начало координат.
1.
2.
3.
в
Признаки уравнения двуполостного гиперболоида:
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Два знака минус в уравнении: один при квадрате переменной
левой части уравнения, другой в правой части при 1.

24. Разные ориентации двуполостного гиперболоида

Каноническое уравнение двуполостного гиперболоида содержит два
знака минус в уравнении.
Один знак минус оставляем в левой части уравнения, а второй
поставим перед единицей в правой части. В таком случае легко
определить ось симметрии гиперболоида: перед квадратом какой
переменной в левой части уравнения знак минус, та ось системы
координат и будет являться осью симметрии.
2
2
2
x
y
z
2 2 1
2
a b
c
| y | b
b
b
x2 y2 z 2
2 2 2 1
a
b
c
| x | a

25. 2. Одно из собственных чисел равно нулю ( ).

2. Одно из собственных чисел
равно нулю ( 3 0).
1 x 2 2 y 2 2b1 x 2b2 y 2b3 z c 0
Выделим полные квадраты
1 ( x
2.1. b3 0
получим
b1
1
) 2 ( y
2
b2
2
) 2 2b3 z c 0
, выполним параллельный перенос
1 ( x ) 2 ( y ) c 0
2
2
x x
y y
z z
b1
1
b2
2

26. 2. Одно из собственных чисел равно нулю ( ).

2. Одно из собственных чисел
равно нулю ( 3 0).
1 x 2 2 y 2 c 0
2.1.1. с=0, знаки 1 , 2 одинаковы. Получим
1 x 2 2 y 2 0
уравнение плоскости
2.1.2. с 0 , знаки 1 , 2 и с одинаковы:
нет решений:
x2 y2
2 1
2
a
b
x2
y2
1
с
с
1
2
-

27. 2. Одно из собственных чисел равно нулю ( ).

2. Одно из собственных чисел
равно нулю ( 3 0).
1 x 2 2 y 2 c 0
2.1.3. с 0 , знаки 1 , 2 одинаковы и отличаются от знака с:
x2
с
1
y2
с
1
2
x2 y2
2 1
2
a
b
- эллиптический цилиндр

28.

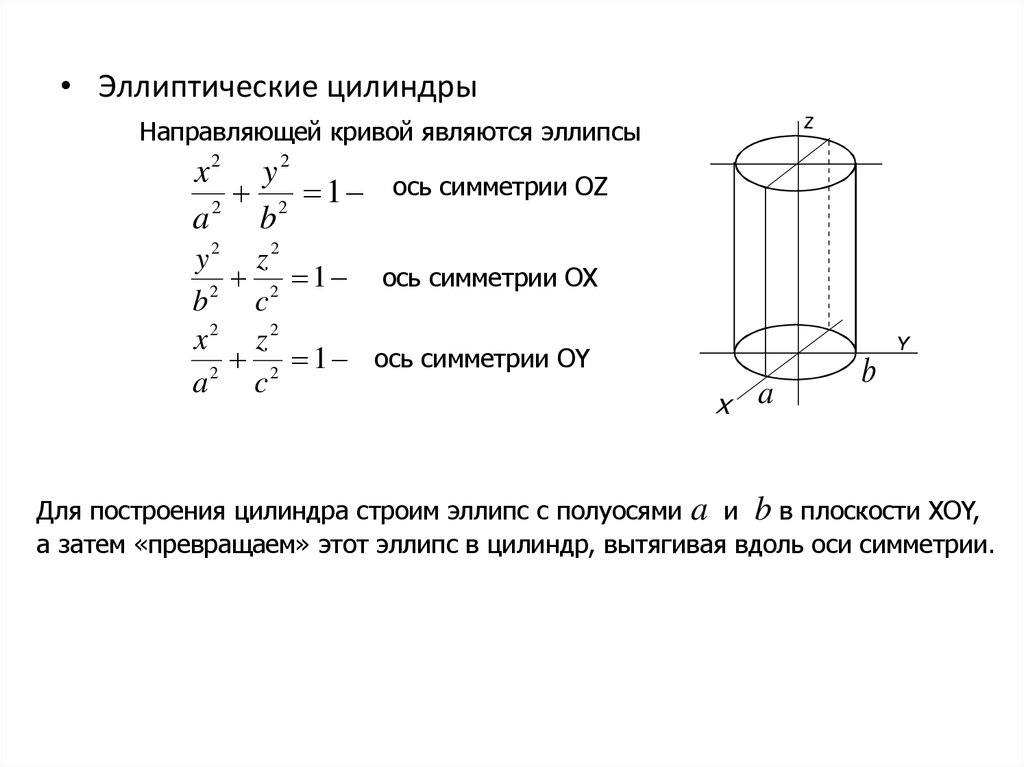
• Эллиптические цилиндры
Направляющей кривой являются эллипсы
x2 y2
2 1
2
a
b
ось симметрии OZ
y2 z2
2 1 ось симметрии OX
2
b
c
x2 z 2
2 1 ось симметрии OY
2
a c
a
b
Для построения цилиндра строим эллипс с полуосями a и b в плоскости XOY,
а затем «превращаем» этот эллипс в цилиндр, вытягивая вдоль оси симметрии.

29. 2. Одно из собственных чисел равно нулю ( ).

2. Одно из собственных чисел
равно нулю ( 3 0).
1 x 2 2 y 2 c 0
2.1.4. с=0, знаки 1 , 2 различны. Получим
1 x 2 2 y 2 0 y 2 x уравнение плоскостей
1
x2
y2
2.1.5. с 0 , знаки 1 , 2 различны:
с
с
получим гиперболический цилиндр:
x2 y2
2 1
2
a
b
1
2
1
-

30.

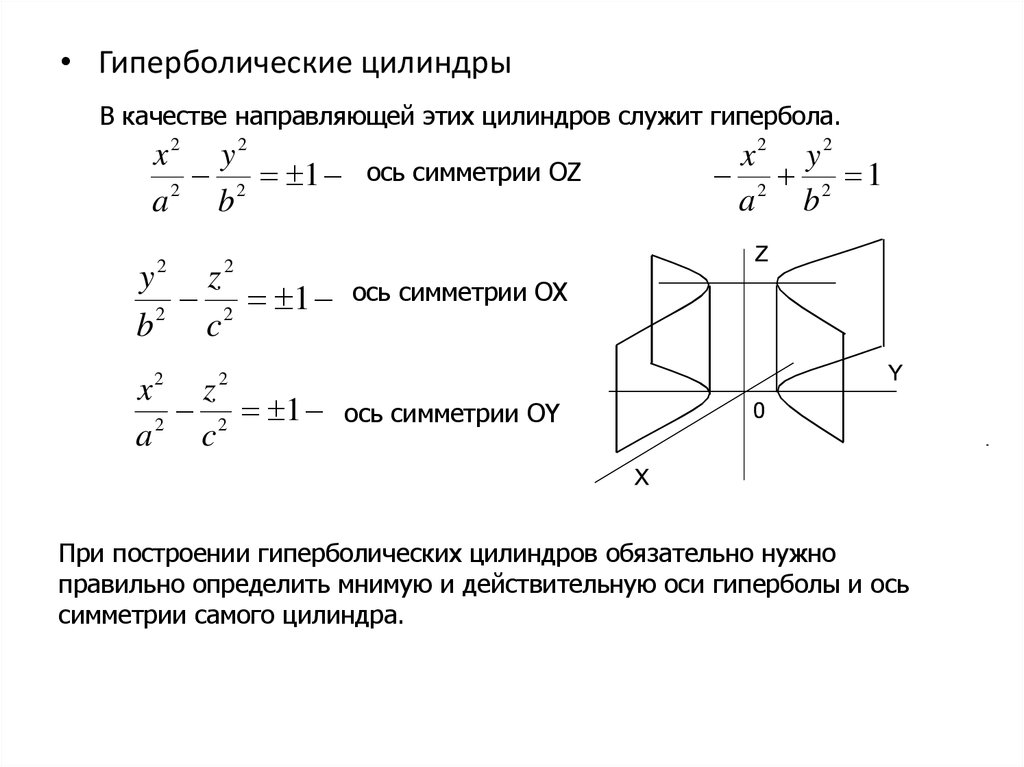
• Гиперболические цилиндры
В качестве направляющей этих цилиндров служит гипербола.
x2 y2
2 1
2
a b
y2 z2
2 1
2
b
c
x2 z 2
2 1
2
a c
ось симметрии OZ
x2 y2
2 2 1
a b
ось симметрии OX
ось симметрии OY
При построении гиперболических цилиндров обязательно нужно
правильно определить мнимую и действительную оси гиперболы и ось
симметрии самого цилиндра.

31. 2. Одно из собственных чисел равно нулю ( ).

2. Одно из собственных чисел
равно нулю ( 3 0 ).
1 x 2 2 y 2 2b1 x 2b2 y 2b3 z c 0
2.2. b3 0
Выделим полные квадраты
c
1 ( x ) 2 ( y ) 2b3 ( z
) 0
1
2
2b3
b1
2
b2
2
выполним параллельный перенос
x x
y y
2
2
(
x
)
(
y
)
2b3 z 0
получим
1
2
b1
1
b2
2
с
z z
2b3

32. 2. Одно из собственных чисел равно нулю ( ).

2. Одно из собственных чисел
равно нулю ( 3 0).
1 x 2 2 y 2 2b3 z 0
Преобразуем
x2
y2
2b3 z
1
1
1
2
Получим каноническое уравнение параболоида
x2 y2
2 2 pz
2
a
b

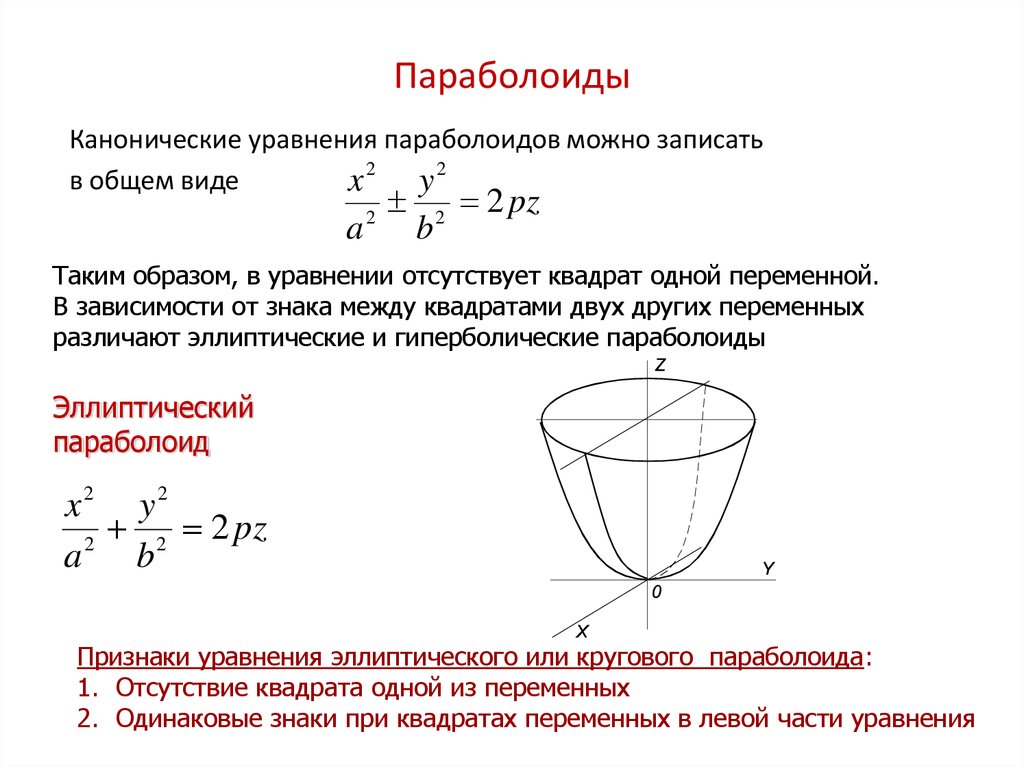
33. Параболоиды

Канонические уравнения параболоидов можно записать
в общем виде
x2 y2
a
2
b
2
2 pz
Таким образом, в уравнении отсутствует квадрат одной переменной.
В зависимости от знака между квадратами двух других переменных
различают эллиптические и гиперболические параболоиды
Эллиптический
параболоид
x2 y2
2 2 pz
2
a
b
Признаки уравнения эллиптического или кругового параболоида:
1. Отсутствие квадрата одной из переменных
2. Одинаковые знаки при квадратах переменных в левой части уравнения

34. Гиперболический параболоид

Каноническое уравнение гиперболического параболоида имеет вид
x2 y2
2 2 2 pz
a
b
Отличительным признаком уравнения гиперболического параболоида
является то что в левой части уравнения между квадратами
переменных знак минус.
Признаки уравнения гиперболического параболоида:
1. Отсутствие квадрата одной из переменных
2. Разные знаки при квадратах переменных в левой
части уравнения
Эта поверхность имеет форму седла.

35. 3. Два собственных числа равны нулю ( ).

3. Два собственных числа равны
нулю ( 2 , 3 0 ).
x 2 2b1 x 2b2 y 2b3 z c 0
Выделим полный квадрат
(x
b1
) 2 2b2 y 2b3 z c 0
выполним параллельный перенос
x x
Получим
y y
z z
( x ) 2 2b2 y 2b3 z c 0
b1

36. 3. Два собственных числа равны нулю ( ).

3. Два собственных числа равны
нулю ( 2 , 3 0 ).
x 2 2b2 y 2b3 z c 0
3.1. b2 , b3 0 , получим
x 2 c 0
Это есть либо уравнения пересекающихся плоскостей, либо
уравнение плоскости или нет решения.

37. 3. Два собственных числа равны нулю ( ).

3. Два собственных числа равны
нулю ( 2 , 3 0 ).
3.2. хотя бы один из
перенос: x x
y y c
2b2
b2 , b3 :0
c
x 2b2 ( y
) 2b3 z 0
2b2
2
x 2 2b2 y 2b3 z 0
z z
поворот:
x x
y y cos z sin ( x ) 2 2b ( y cos z sin ) 2b ( y sin z cos ) 0
2
3
z y sin z cos
( x ) 2 y (2b2 cos 2b3 sin ) z ( 2b2 sin 2b3 cos ) 0
Подбираем угол таким образом, чтобы пропал коэффициент при z:
- параболический цилиндр ( x ) 2 2b y 0
x 2 2 py

38.

• Параболические цилиндры
Направляющей этих цилиндров является парабола.
x 2 2 py
ось симметрии OZ
y 2 2 px
ось симметрии OZ
y 2 2 pz
ось симметрии OX
z 2 2 py
ось симметрии OX
x 2 2 pz
ось симметрии OY
z 2 2 px
x 2 2 py
ось симметрии OY
При построении цилиндра нужно определить основные параметры параболы:
координаты вершины, ось симметрии и направление ветвей, построить
параболу, а затем уже строить цилиндр с соответствующей осью симметрии.