Похожие презентации:
Поверхности второго порядка
1.
Поверхности второго порядка2. Содержание лекции
1. Основные понятия.2.Основные типы поверхностей второго порядка.
3.Методы построения поверхностей второго
порядка.
3.
Уравнение поверхности 2-го порядкаAx By Cz Dx Ey Fz G 0
2
2
Ax2 By 2 Cz 2
2
,
квадратичная часть
Dx Ey Fz G линейная часть
.
К поверхностям 2-го порядка относятся :
сфера, эллипсоид, гиперболоиды, конусы, параболоиды и цилиндры.
Основная задача состоит в умении по уравнению определить тип
поверхности, привести само уравнение к каноническому виду и
построить поверхность в системе координат.
4.
Поверхности второго порядкаГиперболоиды
Цилиндры
Гиперболический
2
2
x y
2 1
2
a b
Параболический
x 2 2 py
Однополостный
2
2
2
Эллиптический
2
2
Двухполостный
x y z
2 2 1
2
a b c
x y
2 1
2
a b
Параболоиды
Эллипсоид
Конус
Сфера
x2 y 2 z 2
2 2 1
2
a b c
x2 y2 z 2
2 2 0
2
a b c
x y z r
2
2
2
2
Эллиптический
Гиперболический
x2 y 2
2z
p q
x2 y2
2z
p q
5.
ЭЛЛИПСОИДЭллипсоидом называется поверхность, которая в некоторой декартовой
системе координат определяется уравнением
где a, b, c>0 — параметры (полуоси) эллипсоида. Это уравнение
называется каноническим уравнением эллипсоида, а система координат,
в которой эллипсоид описывается каноническим уравнением, называется
канонической.
Признаки уравнения эллипсоида:
1. Наличие квадратов всех трех
переменных
2. Одинаковые знаки при квадратах
переменных
3. Разные коэффициенты при
квадратах переменных
6.
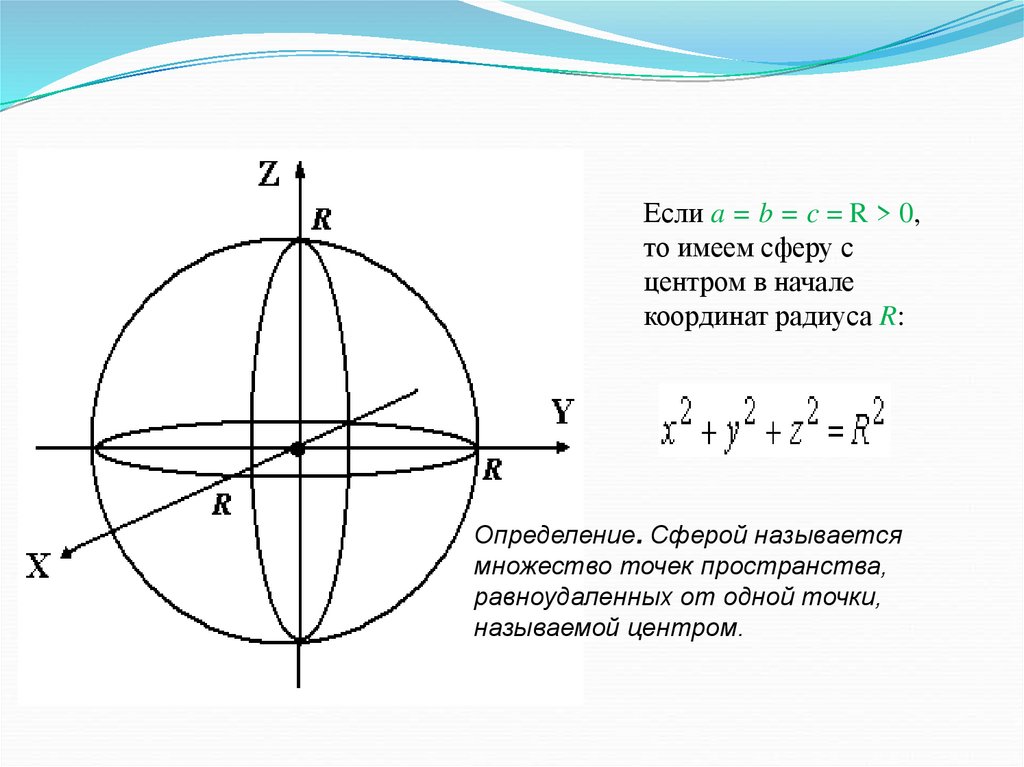
Если a = b = c = R > 0,то имеем сферу с
центром в начале
координат радиуса R:
Определение. Сферой называется
множество точек пространства,
равноудаленных от одной точки,
называемой центром.
7.
Уравнение сферы со смещенным центромO ' ( x0 ; y0 ; z0 )
( x x0 ) 2 ( y y0 ) 2 ( z z0 ) 2 R 2
!
В уравнение сферы входят квадраты трех переменных,
причем коэффициенты при квадратах и знаки
при них одинаковые.
8.
ГИПЕРБОЛОИДЫГиперболоидами называются поверхности, которые в некоторой
декартовой прямоугольной системе координат описываются уравнениями
Однополостным гиперболоидом
называется поверхность, которая в
канонической системе координат
описывается уравнением
Признаки уравнения однополостного гиперболоида:
1. Наличие квадратов всех трех переменных
2. Разные знаки при квадратах переменных
3. Один знак минус при квадрате переменной в левой части уравнения,
в правой части плюс 1.
9. Разные ориентации однополостных гиперболоидов
Ориентация гиперболоида зависит от того, перед какой переменной вканоническом уравнении стоит знак минус.
Однополостный гиперболоид
с осью симметрии OY
2
2
2
x
y
z
2 2 1
2
a b c
c
Однополостный гиперболоид
с осью симметрии OX
x2 y2 z 2
2 2 2 1
a b c
10.
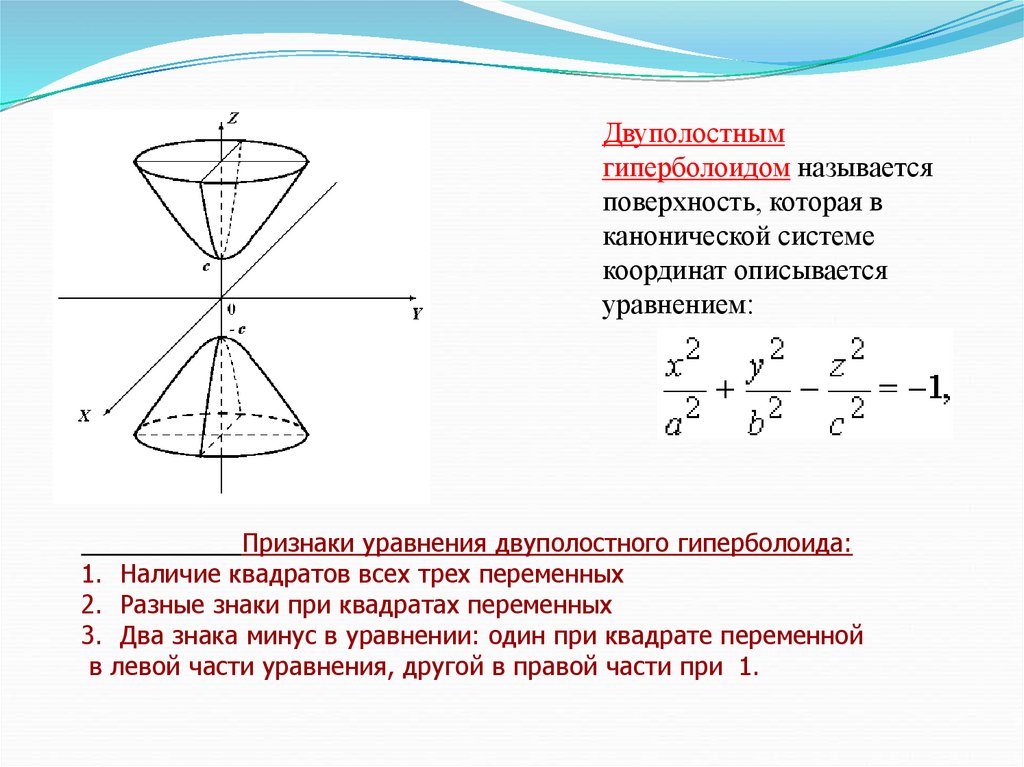
Двуполостнымгиперболоидом называется
поверхность, которая в
канонической системе
координат описывается
уравнением:
Признаки уравнения двуполостного гиперболоида:
1. Наличие квадратов всех трех переменных
2. Разные знаки при квадратах переменных
3. Два знака минус в уравнении: один при квадрате переменной
в левой части уравнения, другой в правой части при 1.
11. Разные ориентации двуполостного гиперболоида
Каноническое уравнение двуполостного гиперболоида содержит два знакаминус в уравнении.
Один знак минус оставляем в левой части уравнения, а второй поставим перед
единицей в правой части. В таком случае легко определить ось симметрии
гиперболоида: перед квадратом какой переменной в левой части уравнения
знак минус, та ось системы координат и будет являться осью симметрии.
2
2
2
x
y
z
2 2 1
2
a b
c
| y | b
b
b
x2 y2 z 2
2 2 2 1
a
b
c
| x | a
12.
ПАРАБОЛОИДЫПараболоидами называются поверхности, которые в некоторой декартовой
прямоугольной системе координат описываются уравнениями:
Эллиптическим параболоидом называется
поверхность, которая в канонической системе
координат описывается уравнением:
Признаки уравнения эллиптического или кругового параболоида:
1. Отсутствие квадрата одной из переменных
2. Одинаковые знаки при квадратах переменных в левой части уравнения
13.
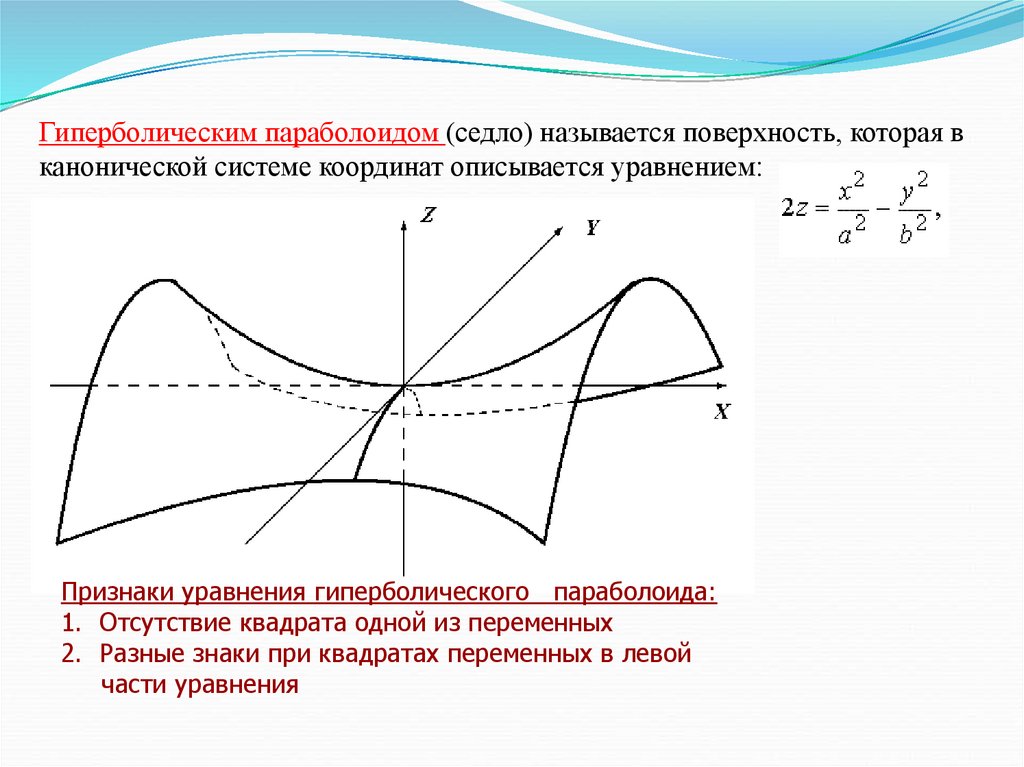
Гиперболическим параболоидом (седло) называется поверхность, которая вканонической системе координат описывается уравнением:
Признаки уравнения гиперболического параболоида:
1. Отсутствие квадрата одной из переменных
2. Разные знаки при квадратах переменных в левой
части уравнения
14. Цилиндрические поверхности
Цилиндрическая поверхность-это поверхность, которую описываетпрямая линия (образующая), которая оставаясь параллельно самой
себе движется вдоль некоторой кривой, называемой направляющей.
По названию направляющей получают свое название и цилиндры.
Если образующая параллельна какой-либо оси координат, то
каноническое уравнение цилиндра не содержит в уравнении
соответствующую переменную. В этом случае уравнение цилиндра
повторяет уравнение своей направляющей. Вариантов различных
уравнений цилиндров достаточно много.
Для построения цилиндра нужно построить направляющую в той
плоскости, в которой она задана, а затем «тянуть» эту линию вдоль той
оси, координата которой отсутствует в уравнении.
Признаки уравнения цилиндрической поверхности:
В уравнении цилиндрической поверхности отсутствует
одна переменная.
15.
16.
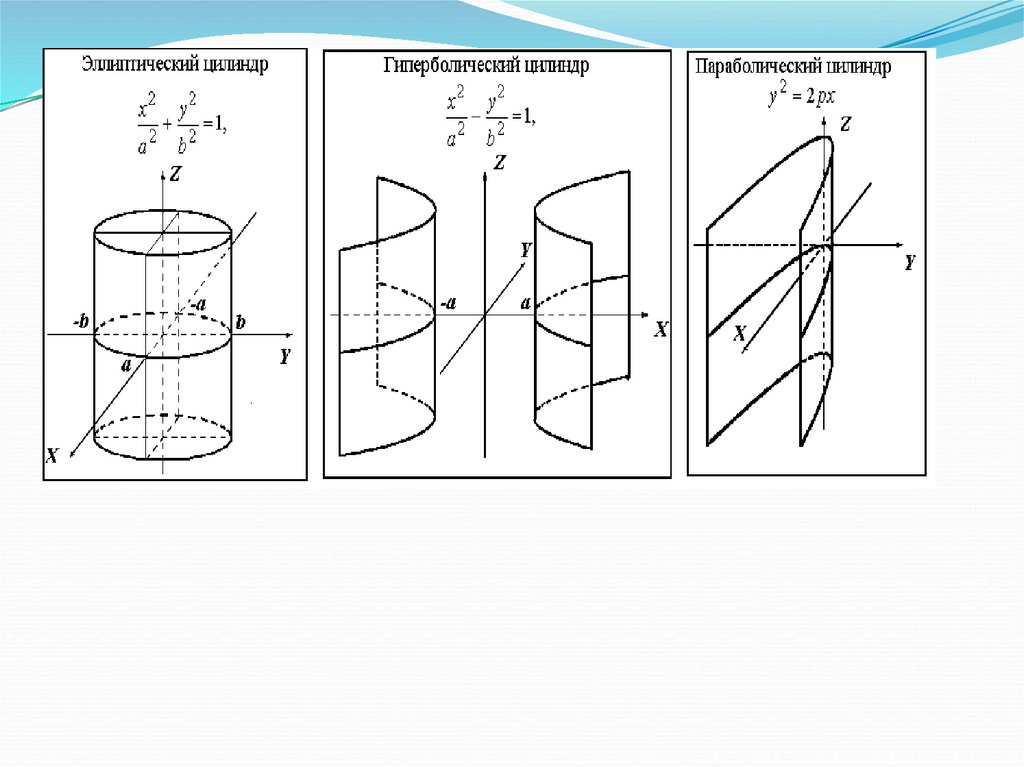
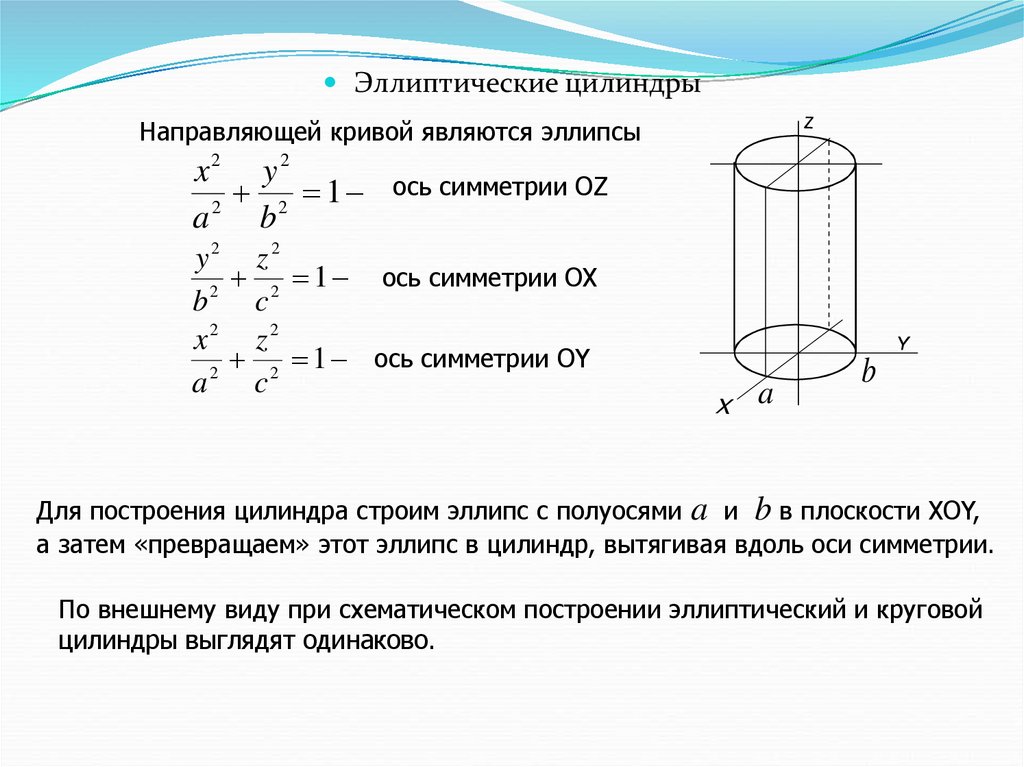
Эллиптические цилиндрыНаправляющей кривой являются эллипсы
x2 y2
2 1
2
a
b
ось симметрии OZ
y2 z2
2 1 ось симметрии OX
2
b
c
x2 z 2
2 1 ось симметрии OY
2
a c
a
b
Для построения цилиндра строим эллипс с полуосями a и b в плоскости XOY,
а затем «превращаем» этот эллипс в цилиндр, вытягивая вдоль оси симметрии.
По внешнему виду при схематическом построении эллиптический и круговой
цилиндры выглядят одинаково.
17.
Гиперболические цилиндрыВ качестве направляющей этих цилиндров служит гипербола.
x2 y2
2 1
2
a b
ось симметрии OZ
x2 y2
2 2 1
a b
y2 z2
2 1 ось симметрии OX
2
b
c
x2 z 2
2 1 ось симметрии OY
2
a c
При построении гиперболических цилиндров обязательно нужно
правильно определить мнимую и действительную оси гиперболы и ось
симметрии самого цилиндра.
18.
Параболические цилиндрыНаправляющей этих цилиндров является парабола.
x 2 2 py ось симметрии OZ
y 2 2 px
ось симметрии OZ
y 2 2 pz
ось симметрии OX
z 2 2 py
ось симметрии OX
x 2 2 pz
ось симметрии OY
z 2 2 px
ось симметрии OY
x 2 2 py
При построении цилиндра нужно определить основные параметры параболы:
координаты вершины, ось симметрии и направление ветвей, построить
параболу, а затем уже строить цилиндр с соответствующей осью симметрии.
19. Конусы 2-го порядка
Каноническое уравнение конусаx2 y2 z 2
2 2 0
2
a
b
c
Каноническое уравнение конуса от уравнений гиперболоидов
отличает то, что в правой части уравнения стоит не единица, а
ноль. Если один знак минус оставляем в левой части уравнения,
то ось симметрии конуса определится также, как и для
гиперболоидов: перед квадратом какой переменной в левой части
уравнения знак минус, та ось системы координат и будет являться
осью симметрии. Для данного уравнения – это ось OZ.
Признаки уравнения конуса:
1. Наличие квадратов всех трех переменных
2. Разные знаки при квадратах переменных
3. Свободный член в правой части уравнения равен нулю.
20. Конусы с разными осями симметрии
Ось симметрии конуса определяется по уравнениюКонус с осью симметрии OY
2
2
2
x
y
z
2 2 0
2
a b
c
Конус с осью симметрии OX
x2 y2 z 2
2 2 2 0
a
b
c
21.
МЕТОДЫ построения поверхностей второго порядкаА) (аналитический)
2
2
3
z
1
2
x
5
y
Построить поверхность
Уравнение определяет эллиптический параболоид (так как
коэффициенты при квадратах переменных различные) с осью симметрии OZ
(так как отсутствует квадрат переменной z) и смещенной также
по оси OZ вершиной
x2 y2
2 2 p( z z0 ),
2
a b
2 x 2 5 y 2 1 3z
2 x 2 5 y 2 3( z 1 / 3)
O ' (0;0;1 / 3) - вершина параболоида
Чаша параболоида направлена вниз, т.е. в отрицательном
направлении оси симметрии
Замечание: наличие коэффициентов при квадратах переменных при
таком схематичном построении можно не принимать во внимание.
22.
Б) (метод сечений)Построить поверхность
z
2
x
+ y2 = z
4
4
Сечение плоскостью YоZ:
x=0,
z=y2
Сечение плоскостью XоZ:
y=0,
z=x2 / 4.
1
2
1
Сечение плоскостью,
параллельной XоY:
z=4,
x2 y 2
1.
16 4
x
Эллиптический параболоид
В) (с использованием ПК…..)
2
у
23.
Проверьте себяОпределите тип поверхности:
1.
x2 y 2 z 2 2 y 9z 1
Сфера со смещённым центром
2.
x 2 y 2 ( z 1) 2
4 1
9
Конус
3.
x2 z 2 y 2
Параболоид (круговой)
4.
x2 z 2 2z
Круговой цилиндр
5.
8 y 2 5z
Параболический цилиндр


















 Математика
Математика








