This lesson is being recorded

1.

Recording Notice
This lesson is
being recorded

2.

King’s Interhigh Logo

3.

Learn 1: Hooke’s Law
Materials – Stiffness

4.

Objectives
Be able to use the Hooke’s law equation, where k is the
stiffness of the object:∆F = k∆x
Be able to draw and interpret force-extension and forcecompression graphs.
Understand the terms limit of proportionality, elastic limit, yield
point, elastic deformation…
…and plastic deformation and be able to apply them to these
graphs.

5.

Page Reference
UK pages 128-135
SLIDE:
5
International pages 84-91

6.

Revision Reminder: Flash cards
An effective retrieval method for regular self-quizzing [retrieve without looking, review
success, shuffle, go again]
SLIDE:
6
Additional tips on
how to create
these cards here

7.

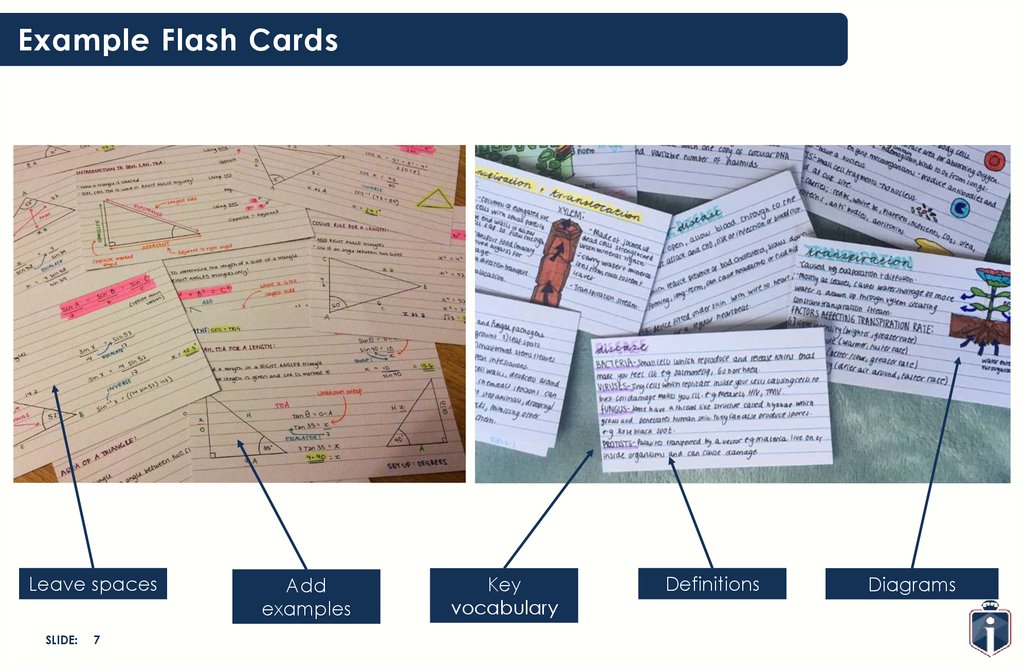
Example Flash Cards
Leave spaces
SLIDE:
7
Add
examples
Key
vocabulary
Definitions
Diagrams

8.

Self quizzing
A retrieval method that helps you master the content you need to know.
SLIDE:
8

9.

Starter
If the arrangement of springs (A) extends
by 1 cm what will (B) extend by?
A. 0.25 cm
B. 0.5 cm
C. 1 cm
D. 2 cm
E. 4 cm
A, they share the force and their
extensions don’t add.
SLIDE:
9
A
B

10.

Forces
Force can change an object’s…
• Speed
• Direction
• Shape
• It is the third one we are interested this week.
• This clip is of a controlled collapse but
somethings failures are not planned.
• Engineers need to understand material to
prevent failures.
Belfast Harbour 0.30 min
SLIDE:
10

11.

AFTER
DURING
BEFORE
AFTER
DURING
BEFORE
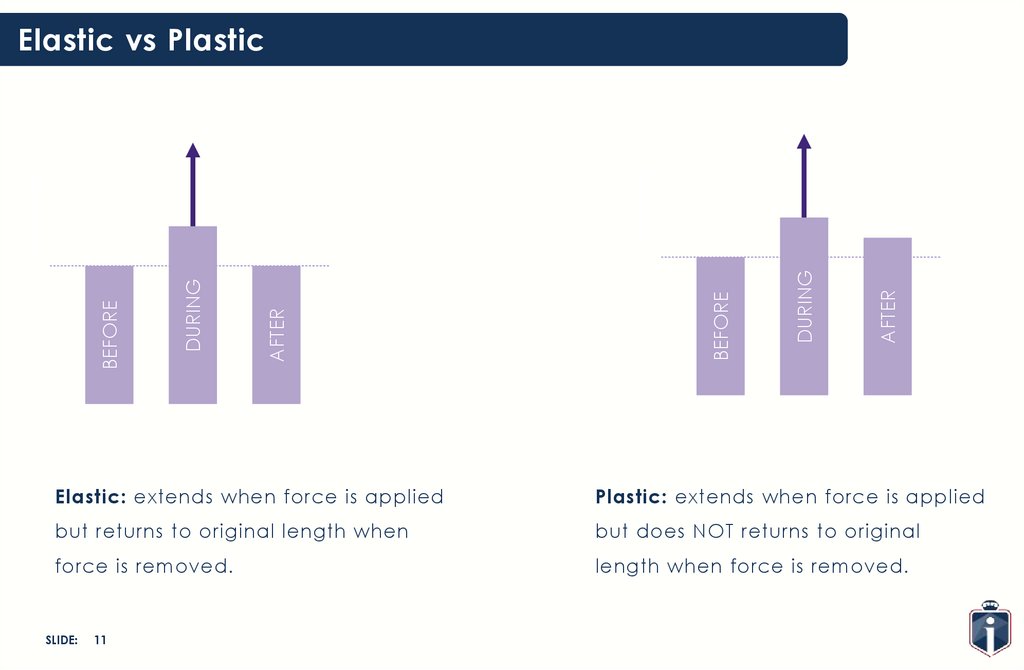
Elastic vs Plastic
Elastic: extends when force is applied
Plastic: extends when force is applied
but returns to original length when
but does NOT returns to original
force is removed.
length when force is removed.
SLIDE:
11

12.

Elastic vs Plastic
Elastic:
Plastic:
Before force
Before force
After force
After force
SLIDE:
12

13.

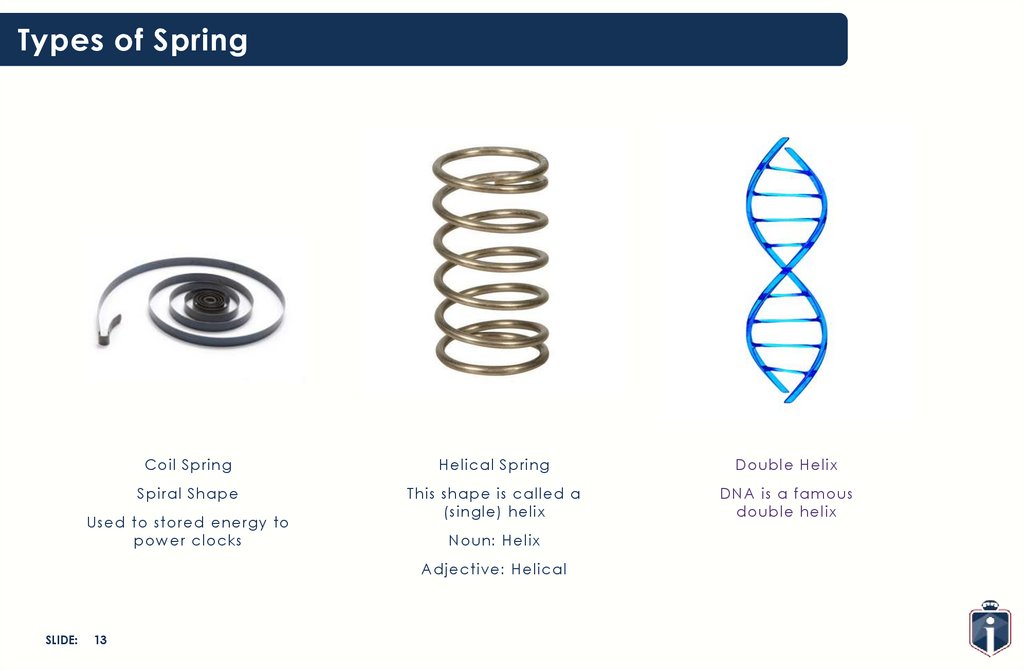
Types of Spring
Coil Spring
Helical Spring
Double Helix
Spiral Shape
This shape is called a
(single) helix
DNA is a famous
double helix
Used to stored energy to
power clocks
Noun: Helix
Adjective: Helical
SLIDE:
13

14.

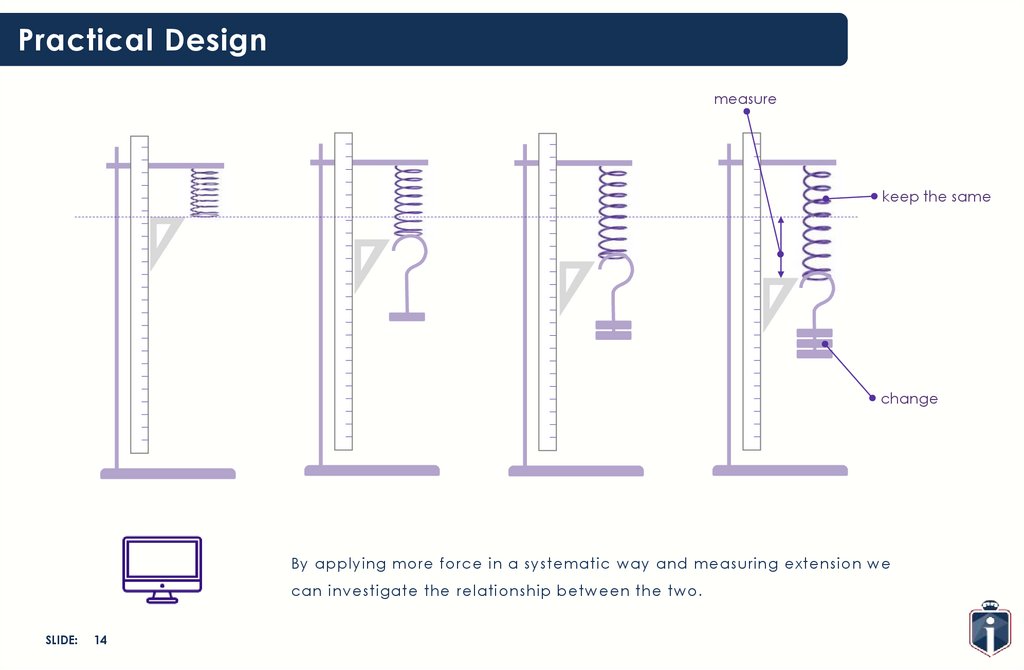
Practical Design
measure
keep the same
change
By applying more force in a systematic way and measuring extension we
can investigate the relationship between the two.
SLIDE:
14

15.

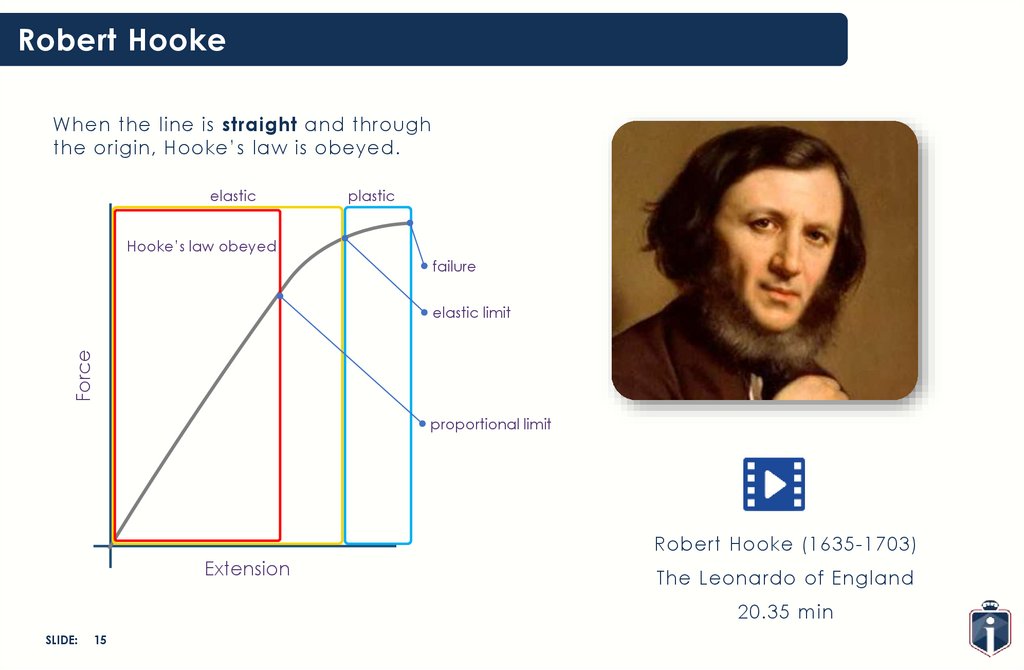
Robert Hooke
When the line is straight and through
the origin, Hooke’s law is obeyed.
elastic
plastic
Hooke’s law obeyed
failure
Force
elastic limit
proportional limit
Robert Hooke (1635-1703)
Extension
The Leonardo of England
20.35 min
SLIDE:
15

16.

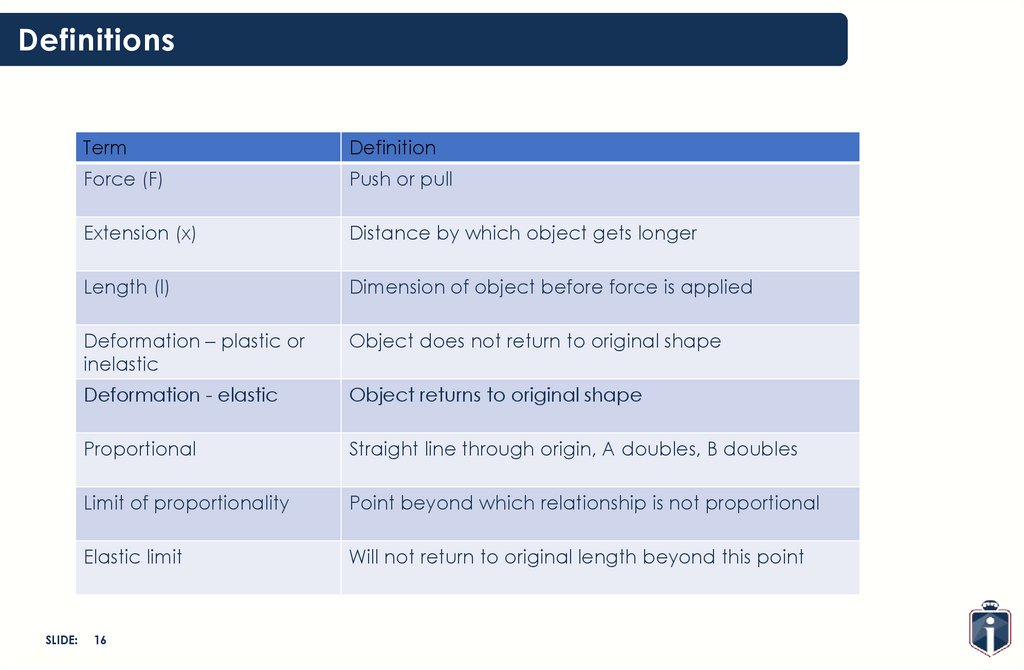
Definitions
SLIDE:
Term
Definition
Force (F)
Push or pull
Extension (x)
Distance by which object gets longer
Length (l)
Dimension of object before force is applied
Deformation – plastic or
inelastic
Object does not return to original shape
Deformation - elastic
Object returns to original shape
Proportional
Straight line through origin, A doubles, B doubles
Limit of proportionality
Point beyond which relationship is not proportional
Elastic limit
Will not return to original length beyond this point
16

17.

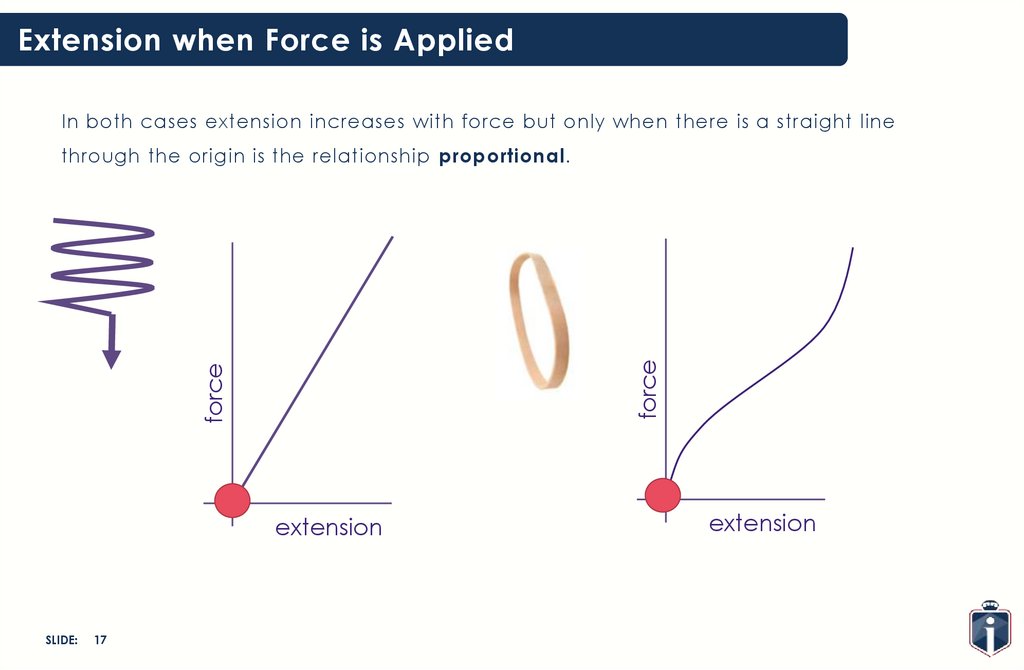
Extension when Force is Applied
In both cases extension increases with force but only when there is a straight line
force
force
through the origin is the relationship proportional.
extension
SLIDE:
17
extension

18.

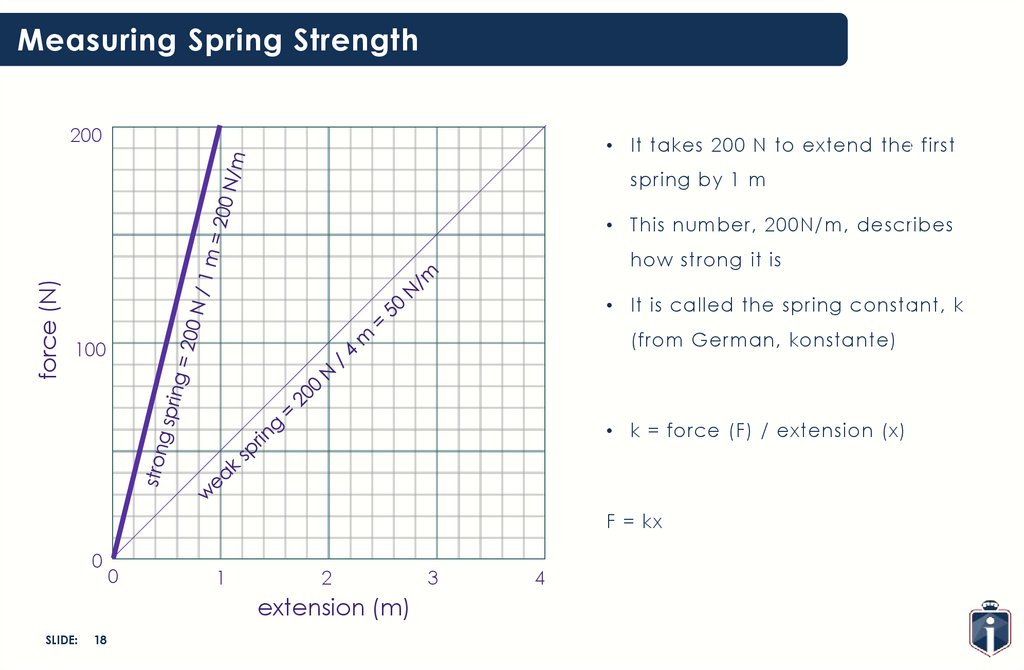
Measuring Spring Strength
200
• It takes 200 N to extend the first
spring by 1 m
• This number, 200N/m, describes
force (N)
how strong it is
• It is called the spring constant, k
(from German, konstante)
100
• k = force (F) / extension (x)
F = kx
0
0
1
2
extension (m)
SLIDE:
18
3
4

19.

F = kx
Words
Force
=
Spring
constant
×
Extension
Symbols
F
=
k
×
x
10N
=
5 N/m
×
2m
Units
F
k
SLIDE:
19
×
x

20.

Plenary
Which if these statements are correct?
While force is applied…
A. Plastic objects extend
B. Elastic objects extend
After force is removed…
C. Plastic objects return to their original length
D. Elastic objects return to their original length
Plasticine
A, B & D are correct.
SLIDE:
20

21.

Learn 2: Stress & Strain
Materials – Stiffness

22.

Objectives I
Be able to calculate the elastic strain energy E el in a deformed
material sample, using the equation: ΔEel = ½ FΔx
…and from the area under the force-extension graph.
The estimation of area and hence energy change for both
linear and non-linear force-extension graphs is expected
SLIDE:
22

23.

Objectives II
Understand how to use the relationships….
tensile or compressive stress = force/cross-sectional area
[σ = F / A]
tensile or compressive strain= change in length/original length
[ε = Δx / x]
SLIDE:
23

24.

Starter
Two business people want to start a
company. One is worth £1 million the
other has just gone bankrupt.
What is their mean net worth?
(1 + 0) / 2 = £0.5 million
SLIDE:
24

25.

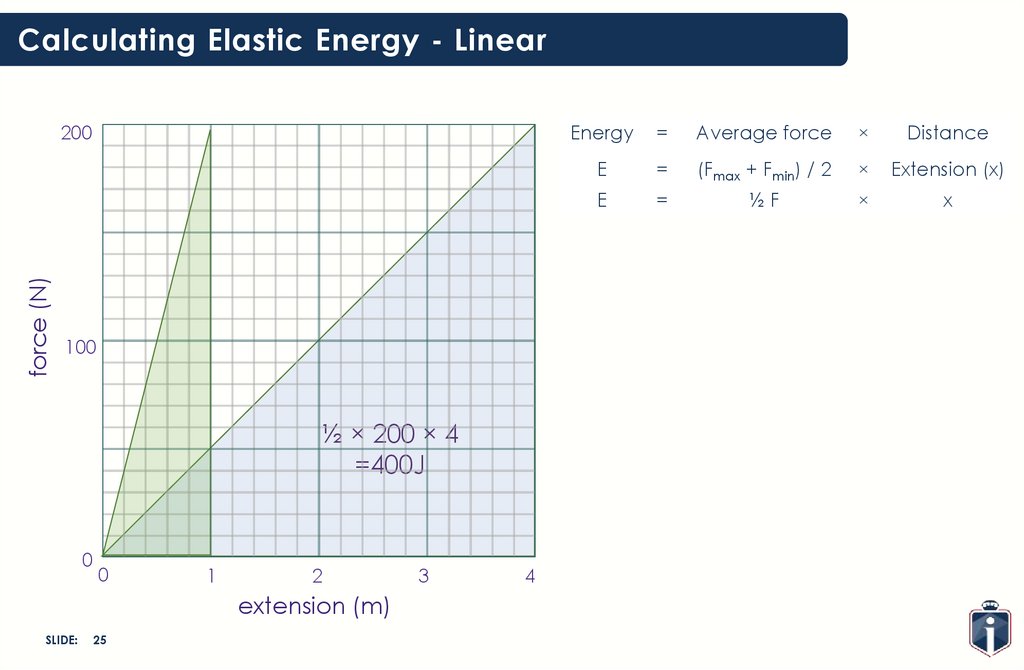
Calculating Elastic Energy - Linear
force (N)
200
100
½ × 200 × 4
=400J
0
0
1
2
extension (m)
SLIDE:
25
3
4
Energy
=
Average force
×
Distance
E
=
(Fmax + Fmin) / 2
×
Extension (x)
E
=
½F
×
x

26.

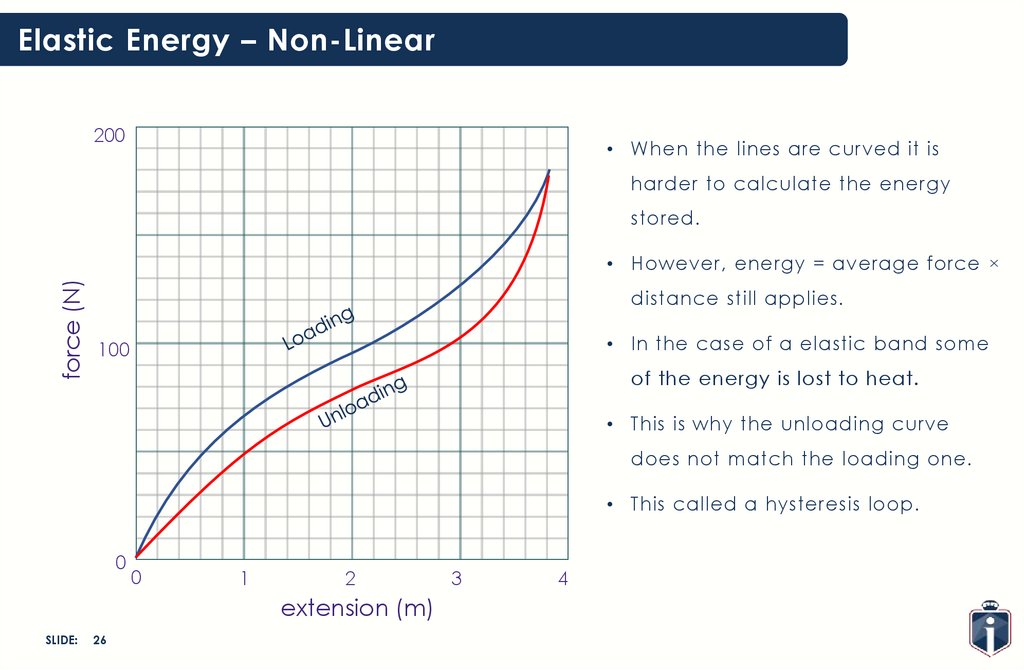
Elastic Energy – Non-Linear
200
• When the lines are curved it is
harder to calculate the energy
stored.
force (N)
• However, energy = average force ×
distance still applies.
• In the case of a elastic band some
100
of the energy is lost to heat.
• This is why the unloading curve
does not match the loading one.
• This called a hysteresis loop.
0
0
1
2
extension (m)
SLIDE:
26
3
4

27.

Substituting
• E = ½kx 2 is a useful new formula
F = kx
E=½
SLIDE:
27
F x =
• It allows us to calculate Energy
½kx2
without force

28.

Comparing Two Metals
In an experiment, the same force was
applied to the two cylinders of the
same start length.
• Was it a fair test?
• If not, why not?
• How could it be improved?
You should only change one variable
at a time by having the same crosssectional area.
SLIDE:
28

29.

Fairer test?
But what if you only had these results?
Is there still something you could do to
make the comparison fair?
• Yes.
• You could calculate force PER crosssectional area.
SLIDE:
29
Name
=
Stress
Formula
=
Force / Area
Symbol
=
σ (sigma)
Unit
=
Nm-2 Pascal (Pa)

30.

Comparing Two Lengths
Two cylinders of the different material, the
same area but different lengths are
compared.
• The left one extends more, can we
conclude it is less stiff?
No.
It is not a fair test, two factors are being
changed.
SLIDE:
30

31.

Fairer Test (Part 2)
Is there something we can do to make it fairer?
Yes.
We can calculate the proportion by which it
extends.
SLIDE:
31
Name
=
Strain.
Formula
=
Extension / Original Length
Symbol
=
ε (Epsilon)
Unit
=
There no unit, it is a ratio

32.

Definitions
SLIDE:
Term
Definition
Stress (σ, sigma)
Done to object: force per unit area
Strain (ε, epsilon)
How object responds: extension compared to original
length
32

33.

I’M FAST
Calculate the stresses on these cylinders, if their diameters are 50 cm and 60 cm.
SLIDE:
33
Step
Detail
Identify
Stress = ?
Mass = 1 kg
Diameter = 50 cm
Diameter = 60 cm
Match
Weight = mg = 1 × 9.81 = 9.81 N
Area = πr2 = 3.14 × 0.252 = 0.196 m2
Area = πr2 = 3.14 × 0.302 = 0.283 m2
Formula
P=F/A
Arrange
-
Substitute
Pblue = 9.81 / 0.196
Pred = 9.81 / 0.283
Total
Pblue = 50.0 Pa
Pred = 34.7Pa

34.

Plenary
Thinking by analogy.
Stress:
External fixed demand of a
situation.
Will the strain of landing a plane
be the same for all people?
• No, it will not.
• An experienced pilot will
experience very little strain.
• An untrained person would
experience massive strain.
SLIDE:
34

35.

Learn 3: Stiffness Value (Young’s Modulus)
Materials – Stiffness

36.

Objectives
Young’s modulus = stress/strain [E = σ / ε]
Be able to draw and interpret tensile or compressive stressstrain graphs…
…and understand the term breaking stress.
CORE PRACTICAL 05: Determine the Young's modulus of a
material.
SLIDE:
36

37.

Starter
Calculate the stresses on these cylinders, if their diameters are 20 cm and 30 cm.
SLIDE:
37
Step
Detail
Identify
Stress (σ) = ?
Mass = 1 kg
Diameter = 20 cm
Diameter = 30 cm
Match
Weight = mg = 1 × 9.81 = 9.81 N
Area = πr2 = 3.14 × 0.12 = 0.0314 m2
Area = πr2 = 3.14 × 0.152 = 0.07065 m2
Formula
σ=F/A
Arrange
-
Substitute
σblue = 9.81 / 0.0314
σred = 9.81 / 0.07065
Total
σblue = 312.4 Pa
σred = 138.9 Pa

38.

Stiffness
How do these factors affect extension?
Force
Length
Area
Stiffness
Extension =
SLIDE:
38

39.

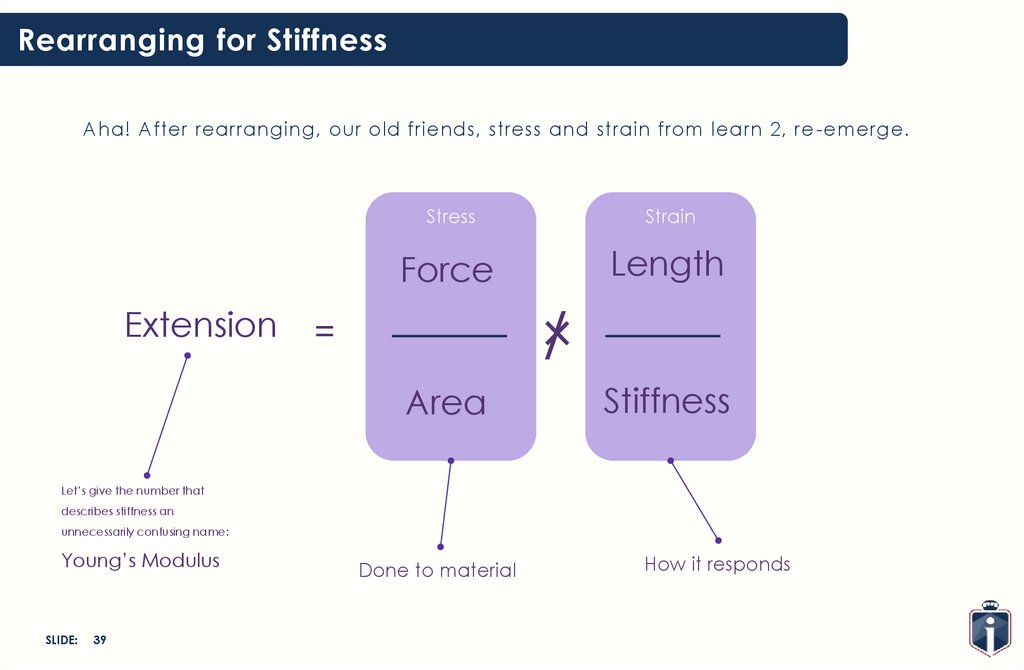
Rearranging for Stiffness
Aha! After rearranging, our old friends, stress and strain from learn 2, re -emerge.
Extension
Stress
Strain
Force
Length
×
/
=
Area
Stiffness
Let’s give the number that
describes stiffness an
unnecessarily confusing name:
Young’s Modulus
SLIDE:
39
Done to material
How it responds

40.

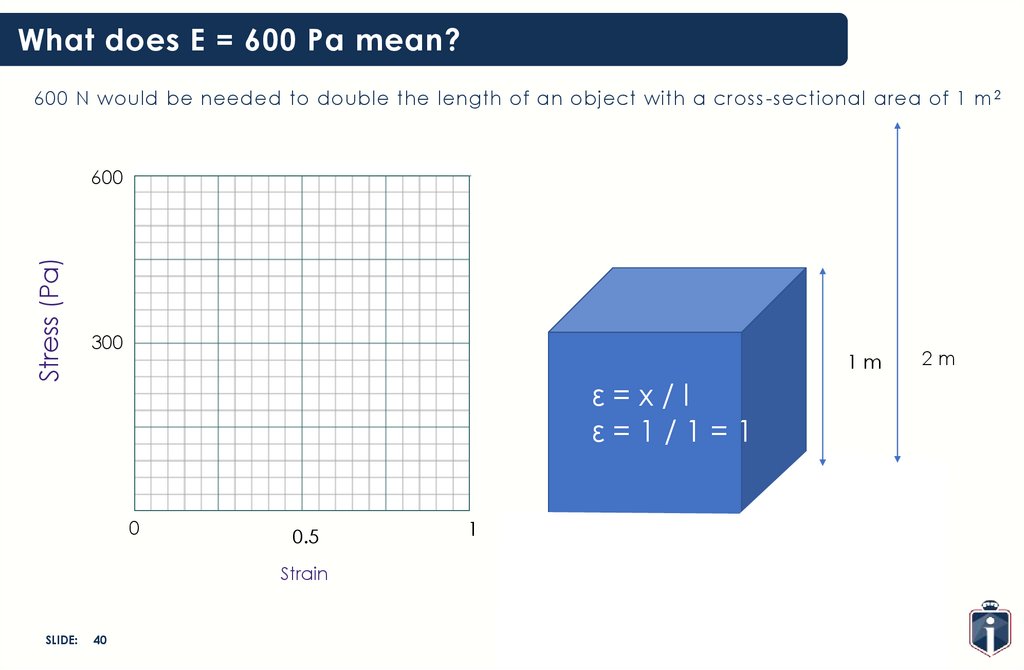
What does E = 600 Pa mean?
600 N would be needed to double the length of an object with a cross -sectional area of 1 m 2
Stress (Pa)
600
300
1m
ε=x/l
ε=1/1=1
0
0.5
Strain
SLIDE:
40
1
2m

41.

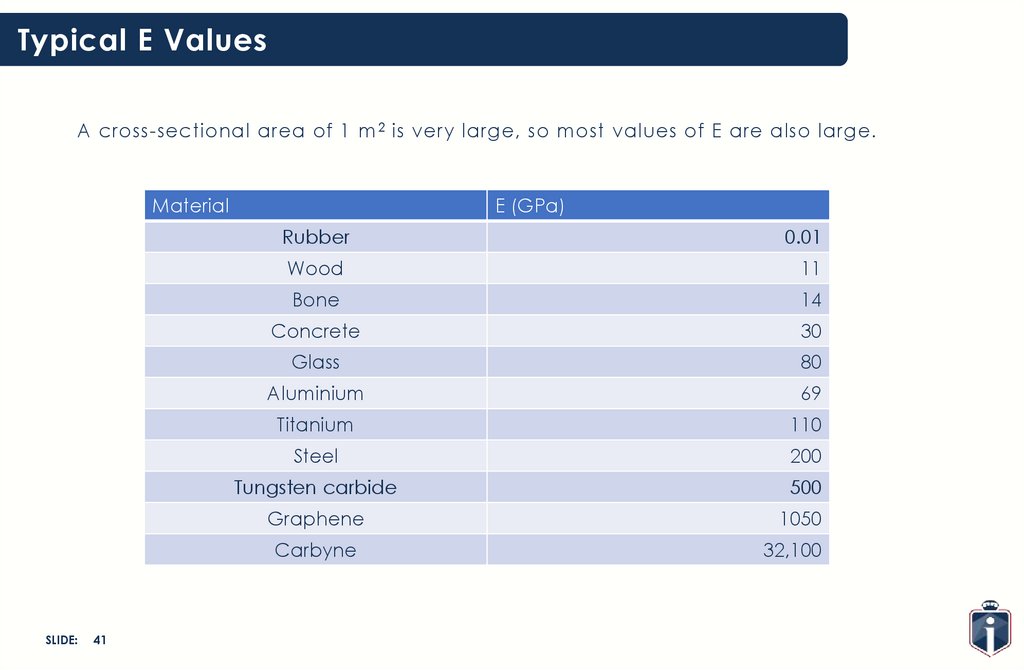
Typical E Values
A cross-sectional area of 1 m 2 is very large, so most values of E are also large.
Material
SLIDE:
41
E (GPa)
Rubber
0.01
Wood
11
Bone
14
Concrete
30
Glass
80
Aluminium
69
Titanium
110
Steel
200
Tungsten carbide
500
Graphene
1050
Carbyne
32,100

42.

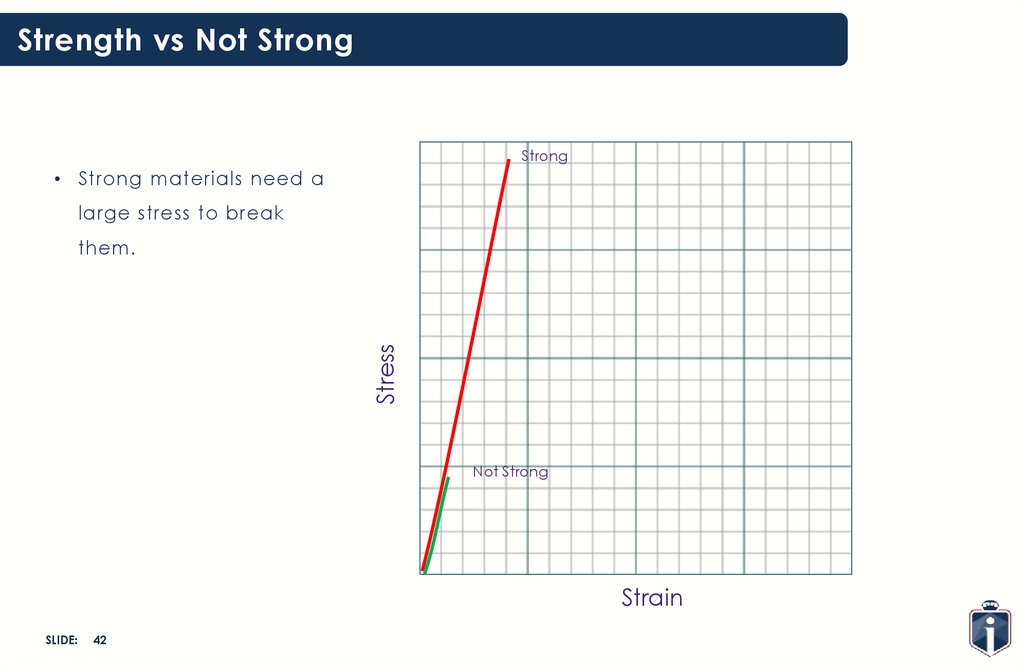
Strength vs Not Strong
Strong
• Strong materials need a
large stress to break
Stress
them.
Not Strong
Strain
SLIDE:
42

43.

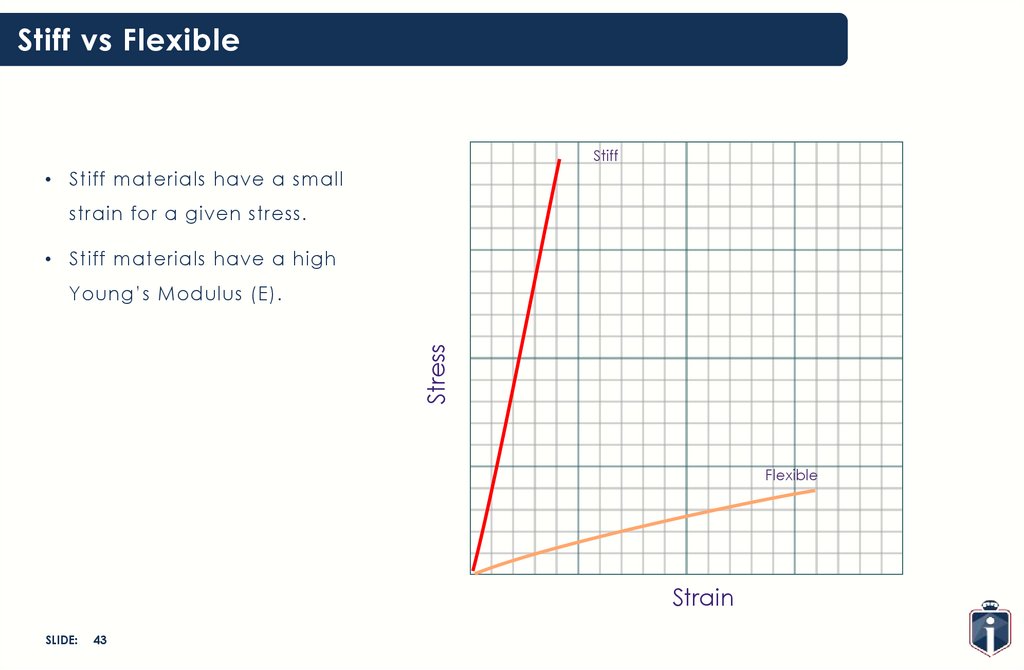
Stiff vs Flexible
Stiff
• Stiff materials have a small
strain for a given stress.
• Stiff materials have a high
Stress
Young’s Modulus (E).
Flexible
Strain
SLIDE:
43

44.

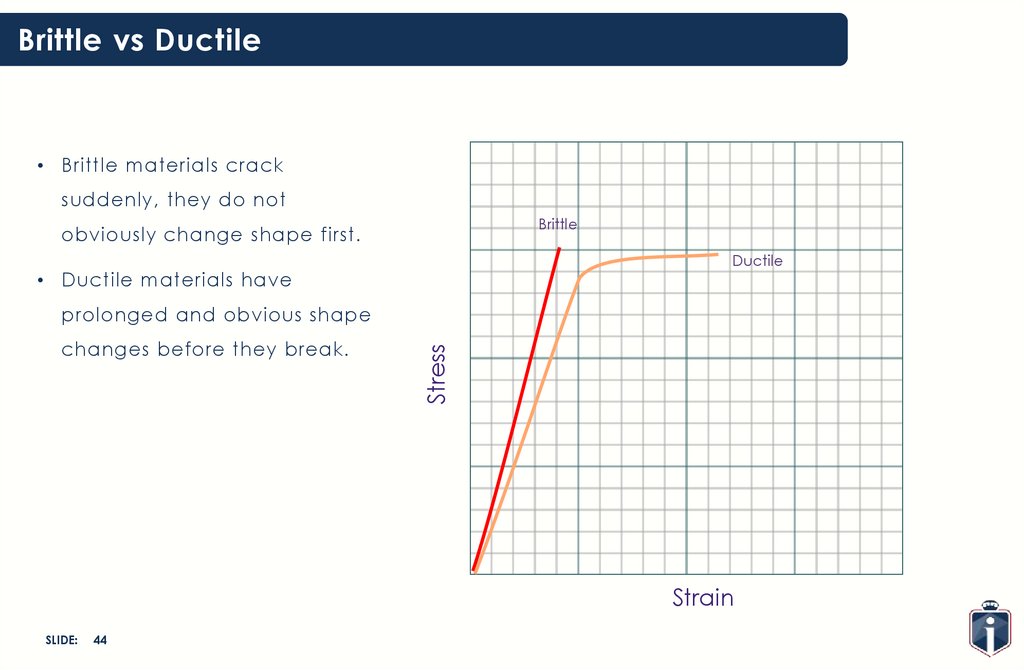
Brittle vs Ductile
• Brittle materials crack
suddenly, they do not
Brittle
obviously change shape first.
Ductile
• Ductile materials have
changes before they break.
Stress
prolonged and obvious shape
Strain
SLIDE:
44

45.

Tough vs Weak
• To be tough a material needs
to be strong and ductile.
• The are under the graph
represents this quantity.
Weak
Stress
Strong + Ductile = Tough
Weak
Strain
SLIDE:
45

46.

Hard vs Soft
• Hard materials resist indentation.
• Soft materials indent easily.
SLIDE:
46

47.

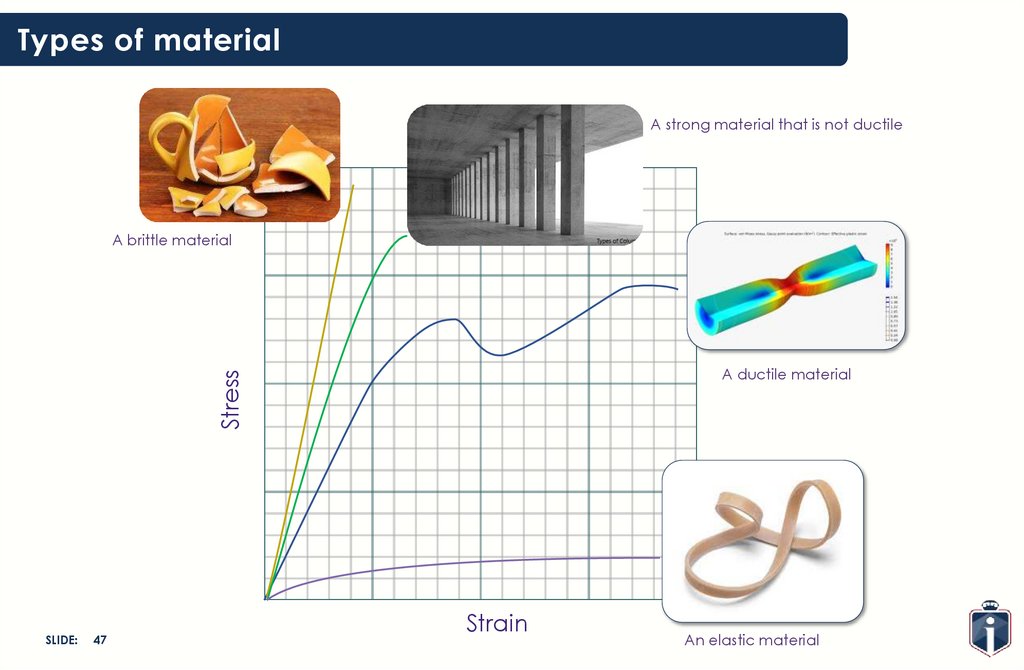
Types of material
A strong material that is not ductile
A brittle material
Stress
A ductile material
SLIDE:
47
Strain
An elastic material

48.

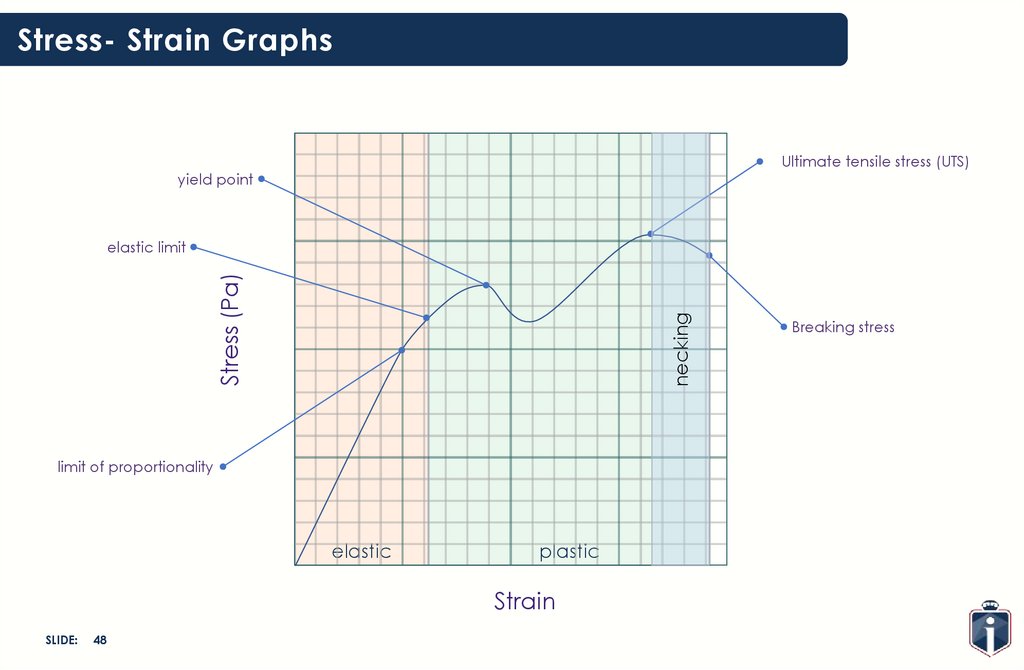
Stress- Strain Graphs
Ultimate tensile stress (UTS)
yield point
necking
Stress (Pa)
elastic limit
limit of proportionality
elastic
plastic
Strain
SLIDE:
48
Breaking stress

49.

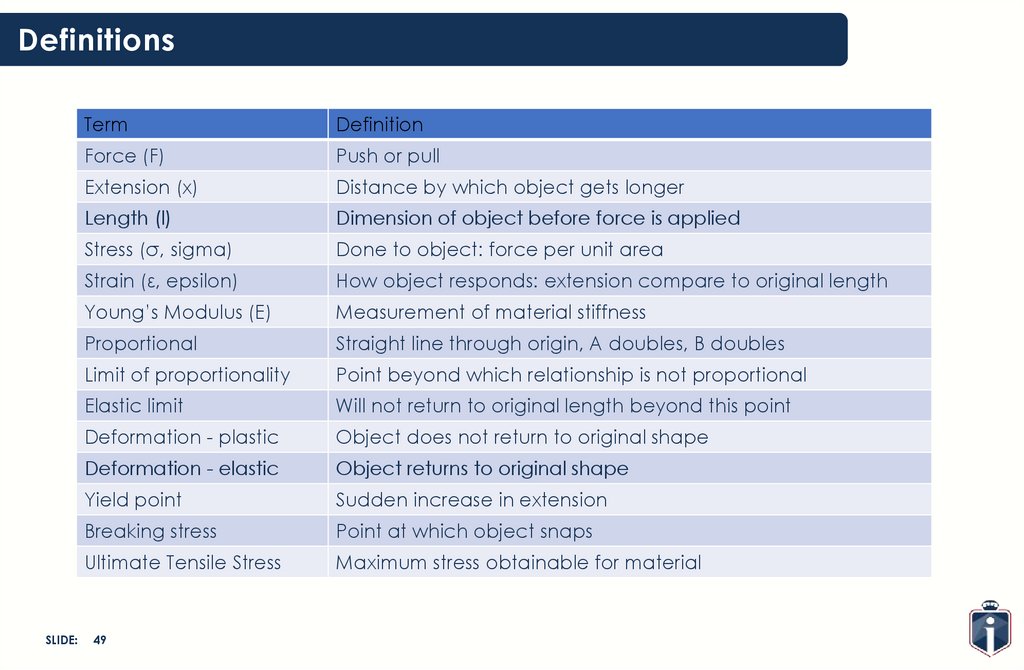
Definitions
SLIDE:
Term
Definition
Force (F)
Push or pull
Extension (x)
Distance by which object gets longer
Length (l)
Dimension of object before force is applied
Stress (σ, sigma)
Done to object: force per unit area
Strain (ε, epsilon)
How object responds: extension compare to original length
Young’s Modulus (E)
Measurement of material stiffness
Proportional
Straight line through origin, A doubles, B doubles
Limit of proportionality
Point beyond which relationship is not proportional
Elastic limit
Will not return to original length beyond this point
Deformation - plastic
Object does not return to original shape
Deformation - elastic
Object returns to original shape
Yield point
Sudden increase in extension
Breaking stress
Point at which object snaps
Ultimate Tensile Stress
Maximum stress obtainable for material
49

50.

Video
Material Properties 101 6.09 min
SLIDE:
50

51.

Optional Prep for next Topic using Century
SLIDE:
51

52.

Plenary
Write an equivalent sentence
F=ma
Mass is a number that allows us to calculate acceleration from force.
E = c mΔθ
Specific heat capacity is a number that allows us to calculate energy from mass and temperature change.
σ = E ε
………………………… is a number that allows us to calculate ……………from …………………
Young’s Modulus is a number that allows us to calculate strain from stress.
SLIDE:
52

53.

Lesson complete!
See you next lesson