Декартово произведение множеств. Лекция № 5.1

1.

ЛЕКЦИЯ №5.1
Декартово произведение
множеств.

2.

План
1. Понятие кортежа.
2. Декартово произведение множеств.

3.

При задании некоторого конечного множества
списком его элементов порядок указания элементов
этого множества не имеет значения. Например,
множества {a, b} и {b, a} совпадают, так как они
состоят из одних и тех же элементов, хотя порядок
указания элементов в этих записях различен. Кроме
этого, каждый элемент входит в множество в
точности один раз, то есть среди элементов
множества нет повторяющихся. Так, запись {a, a}
означает множество, состоящее из единственного
элемента a, то есть {a, a} = {a}.

4.

Введем
новое
исходное
понятие
упорядоченной пары (a, b), которая представляет
собой набор двух объектов a и b, не обязательно
различных, первым элементом которой является a,
а вторым – b.
Определение 1. Упорядоченные пары (a, b) и
(c, d) называются равными, если a = c и b = d.
Пишут (a, b) = (c, d).
В частности, (a, b) = (b, a) a = b .
Сравните: из равенства {a, b} = {b, a} не следует, что a = b.

5.

Обобщением понятия упорядоченной пары является
понятие кортежа – упорядоченного набора произвольных,
не обязательно различных n объектов. Кортеж, состоящий из
элементов x1, x2, …, xn , обозначается (x1, x2, …, xn).
Элементы xi (i = 1, 2, …, n) называются координатами или
компонентами кортежа. Число координат называется
длиной кортежа (размерностью вектора).
Кортежи длины 2 называют также упорядоченными
парами, кортежи длины 3 – упорядоченными тройками и
т.д., кортежи длины n – упорядоченными n-ками. Для
краткости в дальнейшем слово «упорядоченные» будем
опускать.
Кортеж, не содержащий ни одной координаты, т.е.
кортеж длины 0, называется пустым.

6.

Определение 2. Два кортежа (x1, x2, …, xn) и
(y1, y2, …, ym) называются равными, если:
1) n = m; 2) xi = yi (i = 1, 2, …, n).
Пишут (x1, x2, …, xn) = (y1, y2, …, ym).
Основные отличия понятий множества и кортежа
следующие:
в множестве порядок элементов не играет роли, а
кортежи, отличающиеся порядком элементов, различны,
даже в случае, когда они имеют одинаковый состав;
в множестве все элементы различны, а в кортеже
координаты могут повторяться.

7.

Рассмотрим множество В, состоящее из двух
элементов 0 и 1. Кортежи длины n из этих
элементов обозначим Вn. Такие кортежи называют
векторами. Они имеют широкое применение в
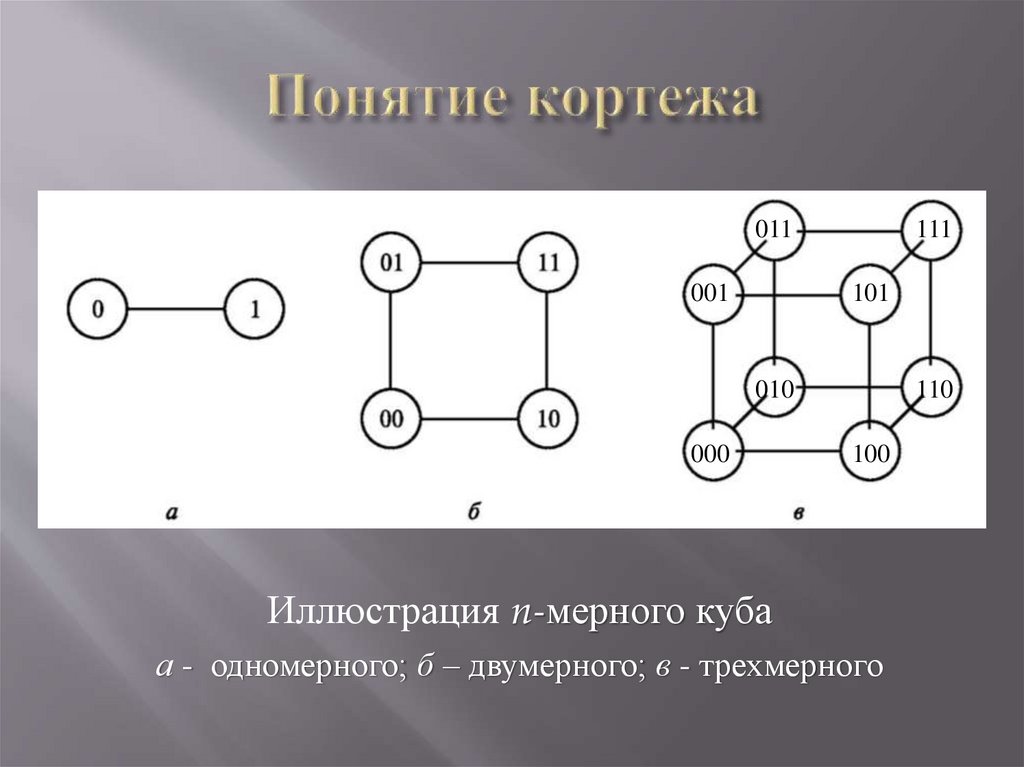
дискретной математике. Каждый такой n-мерный
вектор единственным образом определяет вершину
куба, построенного на единичных векторах. В
зависимости от величины n кубы могут быть
одномерными (а), двумерными (б), трехмерными (в)
и т.д.

8.

011
001
111
101
010
000
110
100
Иллюстрация n-мерного куба
а - одномерного; б – двумерного; в - трехмерного

9.

Вектор, состоящий
из нулей и единиц,
описывает состояние памяти вычислительных
машин, причем память может содержать числа,
тексты, команды и т.д.
Кортежи из нулей и единиц могут быть
сообщениями, передаваемыми по некоторому
каналу связи с помощью импульсов, каждый из
которых принимает одно из двух значений.
Сообщения могут характеризовать результаты
экспериментов: успех (1) или неудачу (0).

10.

Можно
описать
путь
по
некоторой
прямоугольной решетке, определив, например, шаг
вправо через 1, а шаг вверх – через 0. Тогда любой
путь по такой решетке можно задать кортежем.
Так, путь, указанный на
рисунке, определяет кортеж
(1;0;1;1;0;0;1;0;0;1;1;1;1;1;1;0)

11.

Кортеж из единиц и нулей используется также для
кодировки геометрического изображения. Такая
двухцветная
черно-белая
прямоугольная
сетка,
состоящая из черных столбцов на белом фоне, может
быть представлена в виде вектора. В вычислительной
технике широко используется точечное рисование как
растровый рисунок.
Практический прикладной характер кортежей
проявляется в использовании штриховых кодов
(barcodes), которые широко применяются в различных
информационных
системах
для
сообщения
определенной информации о характеристике объекта.

12.

Например, штрих-кодом снабжены товары на базе
или в супермаркете.
Кассовый
компьютер
быстро
считывает
зашифрованную в них информацию. Каждый символ
специальным образом однозначно кодируется
с
помощью полосок черного и белого цвета. Кортеж таких
полосок однозначно переводится в вектор из 0 и 1.

13.

Определение 3. Декартовым (прямым) произведением
множеств А и В называется множество А×В всех кортежей
длины 2 (упорядоченных пар), таких, что x Є A, y Є B, т.е.
A × B= {( x, y ) | x Є A, y Є B}.
Пример 1. Пусть A = {a, b, c} и B ={1, 2}. Тогда
A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)};
B × A = {(1, a), (2, a), (1, b), (2, b), (1, c), (2, c)};
Декартово произведение A × B называется прямым
произведением, а B × A – обратным .
В общем случае, для n множеств A1, A2,…, An
A1 ×A2 × … × An = {( x1, x2, …, xn) | x1Є A1, x2 Є A2, …, xn Є An}.

14.

Если множества А={a1,a2,…,ak} и B={b1,b2,…,bm}
конечны, то их декартово произведение в общем виде
может быть представлено таблицей из k строк и m
столбцов:
Если A1=A2=…=An=А, то множество A×A×…×A
называется n-кратным декартовым произведением
множества A или n-й степенью множества A.
Обозначается Аn. При этом будем считать, что A1 = A.

15.

Задание 1. Найдите декартовы произведения
А ×В, В × А, А ×А, В × В,
если А={1;3}, B={a;b;c}.
A B 1; a , 1; b , 1; c , 3; a , 3; b , 3; c
B A a;1 , b;1 , c;1 , a;3 , b;3 , c;3
A A 1;1 , 1;3 , 3;1 , 3;3
B B a; a , a; b , a; c , b; a , b; b , b; c , c; a , c; b , c; c

16.

Задание 2. Пусть даны множества
A={a,b,c,d,e,f,g,h}, B={1,2,3,4,5,6,7,8}.
Что представляет собой множество А ×В?

17.

Задание 3. Пусть В={0;1}.
Опишите множества В2 , В3 .
Чему равны мощности этих множеств?
Какова мощность множества Вn?
B 0;0 , 0;1 , 1;0 , 1;1
2
B3 0;0;0 , 0;0;1 , 0;1;0 , 0;1;1 , 1;0;0 , 1;0;1 , 1;1;0 , 1;1;1
B 4, B 8
2
3
B 2
n
n

18.

Легко подсчитать, что число элементов декартова
произведения A1 ×A2 × … × An равно
|A1 | |A2 | … |An |, т.е. имеет место формула
| A1 ×A2 × … × An |=|A1 | |A2 | … |An |.
Формулу
числа
элементов
декартова
произведения A1 ×A2 × … × An можно наглядно
изобразить с помощью чертежей особого вида,
называемых «деревьями».

19.

20.

Свойства декартового произведения:
1. Декартово произведение некоммутативно, т.е.
А ×В ≠ В × А.
Пусть А={1}, B={2;3}. Тогда А ×В ={(1;2),(1;3)}, В
×А ={(2;1),(3;1)}.
2. Декартово произведение неассоциативно, т.е.
((А ×В) ×С) ≠ (А×(В×С)).
Пусть А={1}, B={2}, С={3}. Тогда А×В ={(1;2)},
(А×В)×С={(1;2),3}. С другой стороны, В×С={(2;3)} и
А×(В×С) ={1,(2;3)}.

21.

Свойства декартового произведения:
3. Декартово произведение дистрибутивно, т.е.
(А uВ) × С = (А×С) u (В×С);
(А ∩В) × С = (А×С) ∩ (В×С).

22.

Рассмотрим
геометрическую
интерпретацию
декартового произведения двух числовых множеств A и
B – множество всех точек координатной плоскости xOy
с координатами (x, y) такими, что x Є A, а y Є B.
Тогда для двух заданных числовых множеств можно
наглядно изображать их декартово произведение и,
обратно, по изображению прямого произведения двух
множеств определять их элементы.

23.

Пример 2.2. Изобразить на координатной плоскости
xOy A×B, если:
а) A = {3, 5, 7}, B = {2, 4};
б) A = {3, 5, 7}, B = [2; 4];
в) A = [3, 7], B = [2; 4].
Решение.
y
y
y
4
2
4
2
4
2
0
3
а
5 7
х
0
3
б
5 7
х
0
3
в
7
х

24.

Пример 2.3. Определить, прямое произведение каких
множеств A и B изображено на рисунках:
а)
б)
в)
y
y
y
3
2
О
1
1 2 34
х О
1
Решение.
а) А = {1,2,3,4}; B={2}.
б) А = [1;6]; B=[1;3].
в) А = [3;5); B=R.
6
х
О
3
5
х

25.

Задание 4. Найдите декартовы произведения
А ×В, В × А, А ×А, В × В, если

26.

При разработке информационных систем часто
бывает необходимо описывать запросы на
получение информации. Для этого можно
использовать язык теории множеств.
Массивы однородных данных Мi представляют
собой множества, а файл базы данных является
подмножеством М их декартового произведения.
Рассмотрим пример базы данных сотрудников
некоторого отдела внутренних дел:

27.

На языке теории множеств эту таблицу можно описать как
множество М М1×М2×М3×М4×М5, которое представляет собой файл
базы данных, где значения полей данных содержатся в следующих
множествах:
М1 – фамилия, имя, отчество сотрудников
М2 – год рождения
М3 – занимаемая должность
М4 – год поступления на службу
М5 – звание

28.

Будем обозначать через x элементы множества М,
представляющие собой записи базы данных.
Каждый запрос к файлу представляет собой проекцию
множества М, полученную в соответствии с условиями
запроса.
Введем понятие проекции множества.
Пусть М М1×М2×…×Мn и x=(x1, x2, … , xn) –
произвольный вектор (кортеж) из М.
Проекцией вектора x є М на i-тую ось называется его iтая координата и обозначается прi x.
Проекцией множества М на i-тую ось называется
множество всех проекций {прi x, x є М}. Обозначается прi М.

29.

Составим запрос, согласно которому нужно определить
следователей моложе 35 лет со стажем работы в отделе более 5 лет
с указанием фамилий и званий.
Так, множество сотрудников моложе 35 лет есть множество
А1={x: пр2 x )2015-35}, множество следователей: А2={x: пр3 x =
следователь} и множество сотрудников со стажем работы более 5
лет: А3={x: пр4 x (2015-5}. Обозначим А= А1 ∩ А2 ∩ А3 - множество
всех записей о следователях моложе 35 лет и со стажем более 5 лет.
Таким образом, А={Сидоров С.С., 1985, следователь, 2009,
лейтенант милиции}.
Проекция Х = пр1,5 А определяет фамилии и звания требуемых
сотрудников, и, следовательно, является искомым множеством.
Итак, Х = {Сидоров С.С., лейтенант милиции}.