Похожие презентации:
Декартово произведение множеств
1.
ДЕКАРТОВО ПРОИЗВЕДЕНИЕМНОЖЕСТВ
2.
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВСвоё название декартово
произведение получило в честь
выдающегося французского
математика, философа, физика
и естествоиспытателя
Рене Декарта.
Рене Декарт (1596-1650)
3.
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВДекартовым произведением множеств A и B
называется множество АхВ, состоящее из всех
упорядоченных пар вида (а,b), при этом первым
элементом пары является элемент множества А, а
вторым – элемент множества В.
A B a, b a A, b B
4.
ПРИМЕР ДЕКАРТОВА ПРОИЗВЕДЕНИЯКОНЕЧНЫХ МНОЖЕСТВ
.
Задайте декартово произведение множеств A и B
перечислением элементов, если
A 1,3,5
B ,
Решение:
Сначала составим все пары, первое место в которых
займет первый элемент множества A – 1, а на втором
последовательно окажется каждый из элементов
множества В. Таких пар получим две:
1, , 1,
5.
.ПРИМЕР ДЕКАРТОВА ПРОИЗВЕДЕНИЯ
КОНЕЧНЫХ МНОЖЕСТВ
A 1,3,5 B ,
Затем составим все пары, первое место в которых
займет второй элемент множества A – 3, а на втором
последовательно окажется каждый из элементов
множества В. Таких пар получим две:
3, , 3,
6.
ПРИМЕР ДЕКАРТОВА ПРОИЗВЕДЕНИЯКОНЕЧНЫХ МНОЖЕСТВ
A 1,3,5 B ,
Составим все пары, первое место в которых займет
третий – последний элемент множества A – 5, а на
втором последовательно окажется каждый из
элементов множества В. Таких пар получим две:
5, , 5,
7.
ПРИМЕР ДЕКАРТОВА ПРОИЗВЕДЕНИЯКОНЕЧНЫХ МНОЖЕСТВ
A 1,3,5
B ,
A B 1, , 1, , 3, , 3, , 5, , 5,
8.
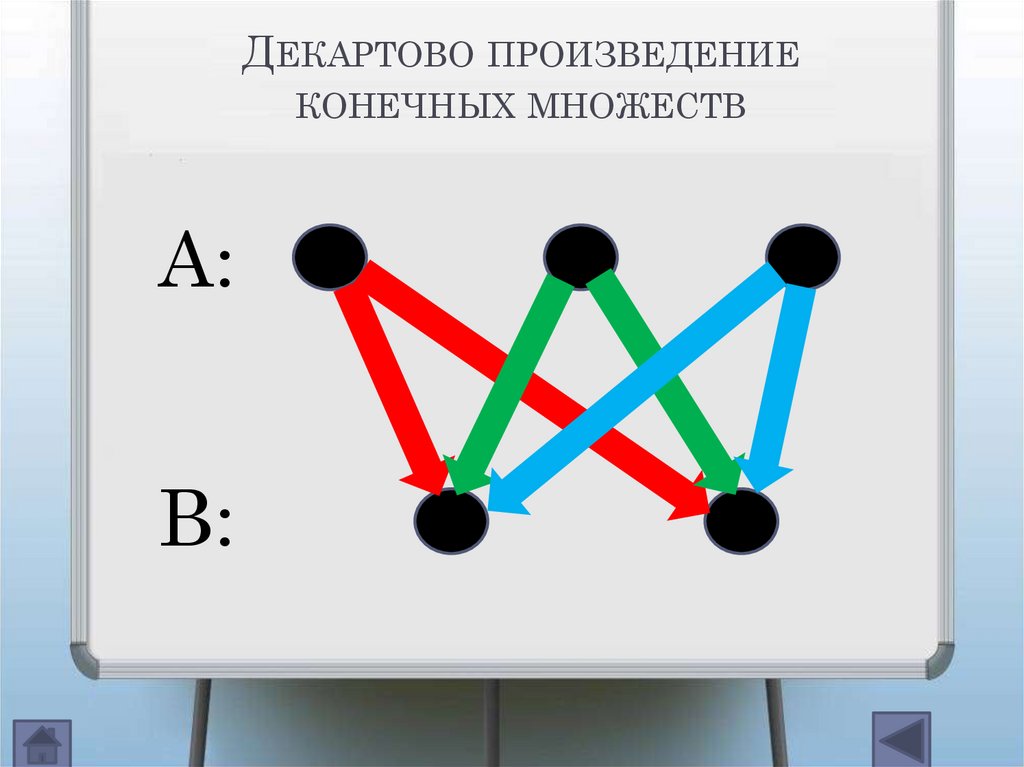
ДЕКАРТОВО ПРОИЗВЕДЕНИЕКОНЕЧНЫХ МНОЖЕСТВ
А:
B:
9.
ЗАДАНИЕ ДЕКАРТОВА ПРОИЗВЕДЕНИЯКОНЕЧНЫХ МНОЖЕСТВ ТАБЛИЦЕЙ
Декартово
произведение
двух
конечных
множеств В и А в ряде случаев удобно задавать
таблицей.
Для этого элементы множества В размещают в
первом столбце таблицы, элементы множества А – в
первой строке и формируют пары: элемент строки –
элемент столбца.
Пример:
Задайте декартово произведение множеств B и A
таблицей, если
B , A 1,3,5
10.
ЗАДАНИЕ ДЕКАРТОВА ПРОИЗВЕДЕНИЯКОНЕЧНЫХ МНОЖЕСТВ ТАБЛИЦЕЙ
B ,
B A
A 1,3,5
3
5
1
( , ) ( , ) ( , )
( , ) ( , ) ( , )
11.
ЗАДАНИЕ ДЕКАРТОВАПРОИЗВЕДЕНИЯ ЧИСЛОВЫХ МНОЖЕСТВ
ГЕОМЕТРИЧЕСКИ
Декартово
произведение
двух
числовых
множеств A и B можно задать геометрически в
прямоугольной декартовой системе координат на
плоскости.
Для этого элементы множества A откладываются
по оси абсцисс, а элементы множества B – по оси
ординат.
Элементами собственно декартова произведения
являются точки плоскости.
12.
ПРИМЕР ЗАДАНИЯ ДЕКАРТОВАПРОИЗВЕДЕНИЯ ЧИСЛОВЫХ МНОЖЕСТВ
ГЕОМЕТРИЧЕСКИ
Изобразите геометрически декартово произведение
множеств A и B, если:
A a a 1;3 B 3,1,2,4
13.
ПРИМЕР ЗАДАНИЯ ДЕКАРТОВАПРОИЗВЕДЕНИЯ КОНЕЧНЫХ МНОЖЕСТВ
ГЕОМЕТРИЧЕСКИ
A a a 1;3
B 3,1,2,4
y
4
2
1
-1 0
1
-3
3
x












 Математика
Математика








