Функция. Область определения и область значений функции. Урок 1

1.

30.01.2024
Классная работа
Уч. математики. Демидова Я.И.
МБОУ «Орловская СОШ»

2.

Разминка
• Вставьте пропущенные значения, если y
X
Y
-5
-3
0
3
= 2x+5
12
10
19
53
• Как называется зависимость, выраженная данной формулой
y = 2x+5 ?
• Какая переменная в этом случае независимая, x или y?
• Почему y называется зависимой переменной?
• Если дана функция, сколько значений может иметь переменная
y при каком-либо значении x?

3.

Тема урока
ФУНКЦИЯ. ОБЛАСТЬ
ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
ЗНАЧЕНИЙ ФУНКЦИИ.
Урок 1

4.

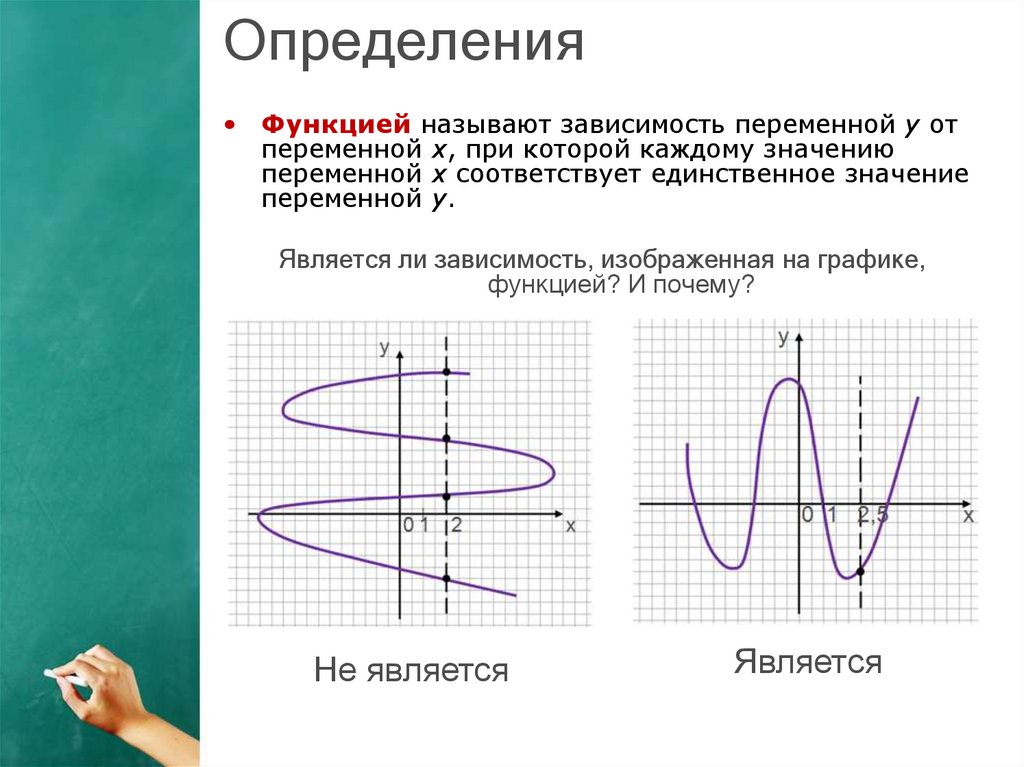
Определения
• Функцией называют зависимость переменной y от
переменной x, при которой каждому значению
переменной x соответствует единственное значение
переменной y.
Является ли зависимость, изображенная на графике,
функцией? И почему?
Не является
Является

5.

Определения
• Переменную x называют независимой переменой
или аргументом.
• Переменную y называют зависимой переменной или
функцией от x. Значения зависимой переменной
называют значениями функции.
Обозначение: y = f(x).
Замечание: вместо f может быть g, φ и др.
• Область определения функции – все значения
независимой переменной, обознач. D(f).
• Область значений функции – все значения
зависимой переменной, обознач. E(f).
Найти область определения функции:
f(x) = 3x²+27
(все значения х)
(x не равен 7)

6.

Практика
• Найдите значение функции при
заданном значении аргумента
1. f(x)=4x²-9
f(0)=? f(-2)=? f(1,5)=?
f(0)=4•0-9=-9,
f(-2)=4•(-2)²-9=4•4-9=16-9=7,
f(1,5)=4•1,5²-9=4•2,25-9=9-9=0.

7.

Практика
• Найдите значение функции при
заданном значении аргумента
2.
при x = 3; -2; 4.
f(3)=12,
f(-2)=2,
f(4)=Ø (нет решения).

8.

Практика
• Найдите значение функции при
заданном значении аргумента
3.
g(1)=?
g(-1)=?
При каком значении x решений
нет?
g(1)=1,
g(-1)=5,
g(1,5)=Ø (нет решения).

9.

Практика
4. Найдите значения x, при которых
φ(x)=0
1) φ(x)=2x(x-9)
x=±3
2)
x=-7
5. Известно, что g(x)=-6x+11. Найдите
значение x, при котором
g(x)=-1,
x=2,
g(x)=5,
x=1,
g(x)=20.
x=-1,5.

10.

Практика
6. Найдите область определения
функции
а) y=x²+2x
D(f)=(-∞;+∞) или xϵ(-∞;+∞)
б)
D(f)=(-∞;-1)U(-1;+∞)
или xϵ(-∞;-1)U(-1;+∞)
в)
D(f)=[-9;+∞)
или xϵ[-9;+∞)

11.

Домашнее задание
§1.п.1, № 1, 5, 7, 9.
Рефлексия
Урок
Я на уроке
Итог
1. Интересно
1. Работал
1. Понял
материал
2. Скучно
2. Отдыхал
2. Узнал больше,
чем знал
3. Безразлично
3. Помогал
другим
3. Не понял

12.

30.01.2024
Тема урока
ФУНКЦИЯ. ОБЛАСТЬ
ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
ЗНАЧЕНИЙ ФУНКЦИИ.
Урок 2. Графики функций

13.

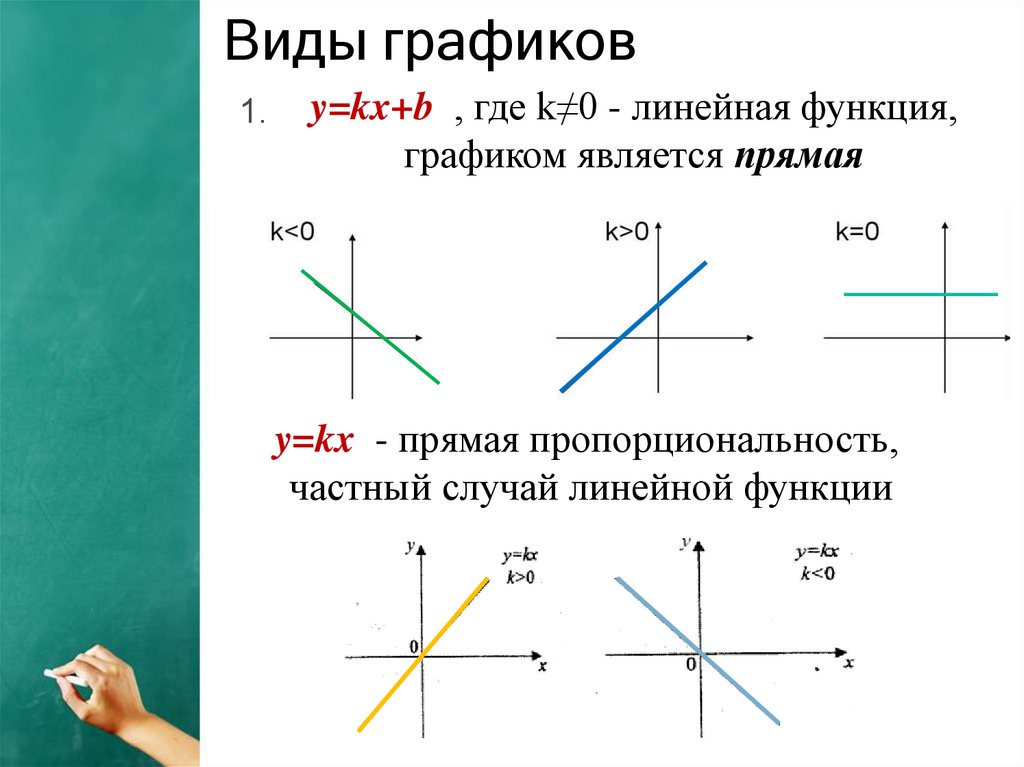
Виды графиков
1.
y=kx+b , где k≠0 - линейная функция,
графиком является прямая
y=kx - прямая пропорциональность,
частный случай линейной функции

14.

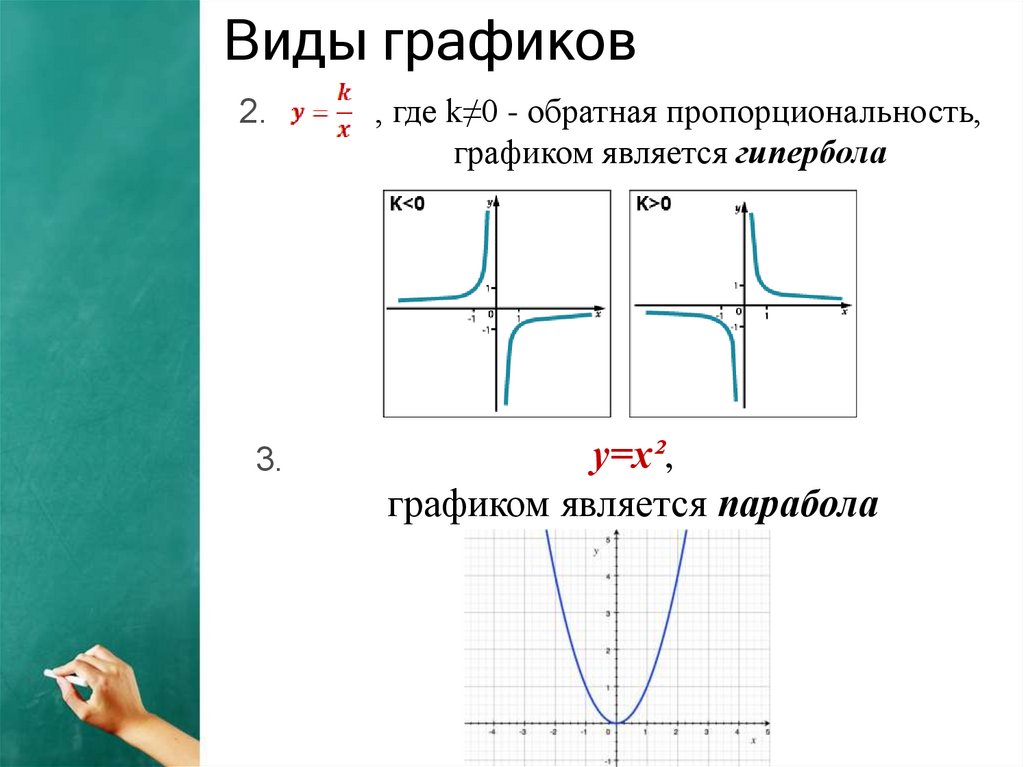
Виды графиков
2.
3.
, где k≠0 - обратная пропорциональность,
графиком является гипербола
y=x²,
графиком является парабола

15.

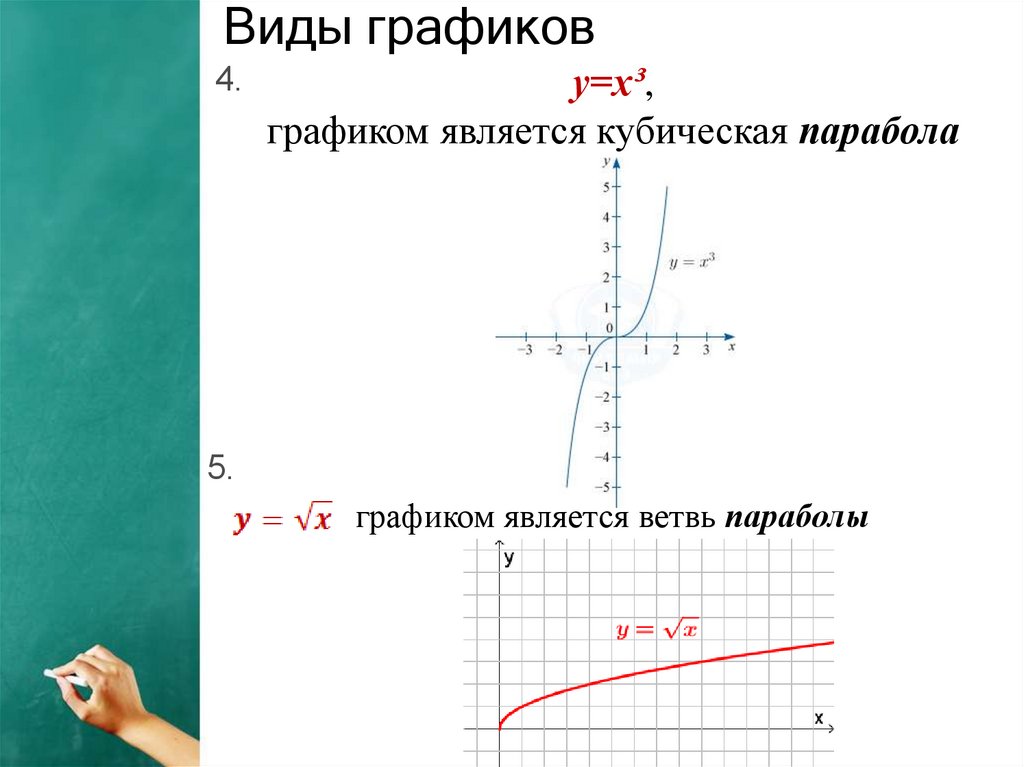
Виды графиков
4.
y=x³,
графиком является кубическая парабола
5.
графиком является ветвь параболы

16.

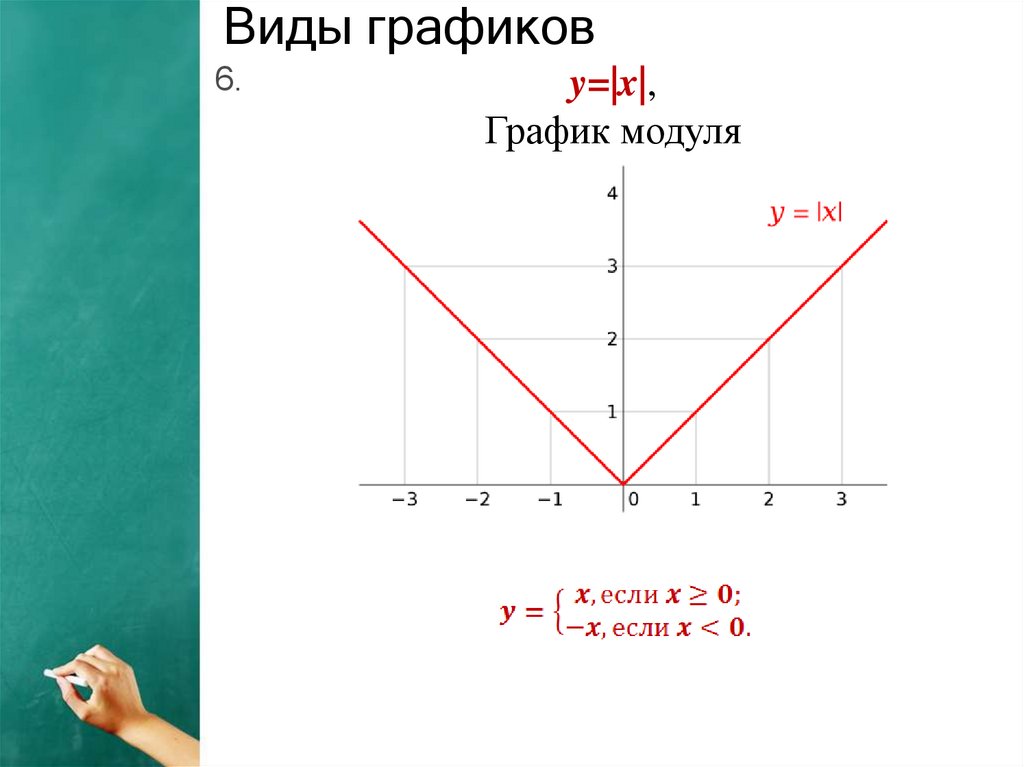
Виды графиков
6.
y=|x|,
График модуля

17.

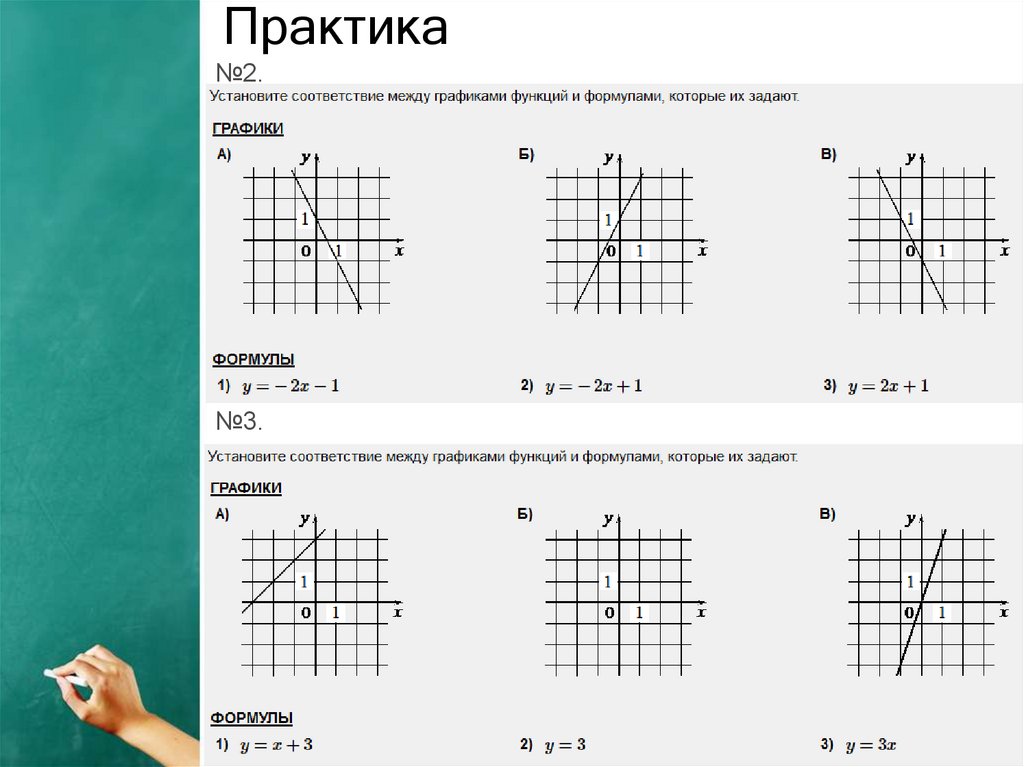
Практика
№1.

18.

Практика
№2.
№3.

19.

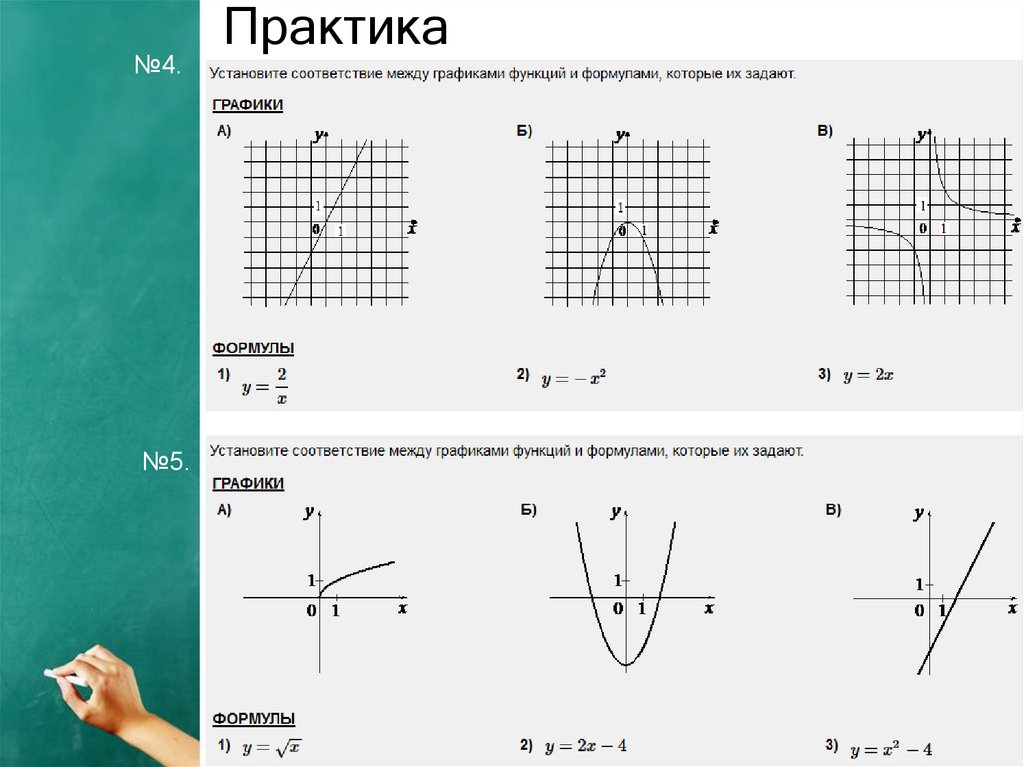
№4.
№5.
Практика

20.

Домашнее задание
§1.п.1. № 22, 23, 28
Рефлексия
1. Урок полезен, всё понятно
2. Лишь кое-что чуть-чуть неясно
3. Еще придется потрудиться
4. Да! Трудно все-таки учиться!