Область определения функции

1. Урок математики.

«С тех пор как существует
мирозданье,
Такого нет, кто б не нуждался
в знанье.
Какой мы ни возьмем язык и
век,
Всегда стремится к знанью
человек »

2.

3. Основные этапы урока:

Математическая
разминка.
Устная коллективная работа.
Самостоятельная работа в группах.
Рефлексия.

4. Разминка 1 команда.

Как называется переменная
образующая область определения
функции?
Какая ось определяет значения
аргумента?
Как кратко записать «область значения
функции»
Как называется функция, график
которой – прямая?

5. Продолжение разминки

Каким числом не может быть
показательная функции?
Что есть в земле, в слове и в уравнение?
Сколько корней может иметь квадратное
уравнение?
Как называется раздел математики,
который изучает свойства фигур?
Что такое функция?

6. Разминка 2 команда

Как называется переменная которая
образует область значения функции?
Какая ось определяет значения
функции?
Как кратко записать «область
определения функции»?
Как называется функции, графиком
которой является парабола?
Что такое уравнение?

7. Продолжение разминки

Сколько
корней может иметь
линейное уравнение?
Что легче 1 кг. Железа или 1 кг.
Пуха?
Как называется раздел математики,
который изучает производную и
первообразную функции?
Что общего между качелями,
музыкой и светом?

8. Основные вопросы урока.

Что
такое функция?
Что такое область определения
функции?
Что такое график функции?
Основные условия существования
функции?

9. Определение функции

Функцией
называется зависимость
одной переменной от другой, при
котором каждому значению
независимой переменной
соответствует единственное значение
зависимой переменной.
Обозначают: у= f(x)

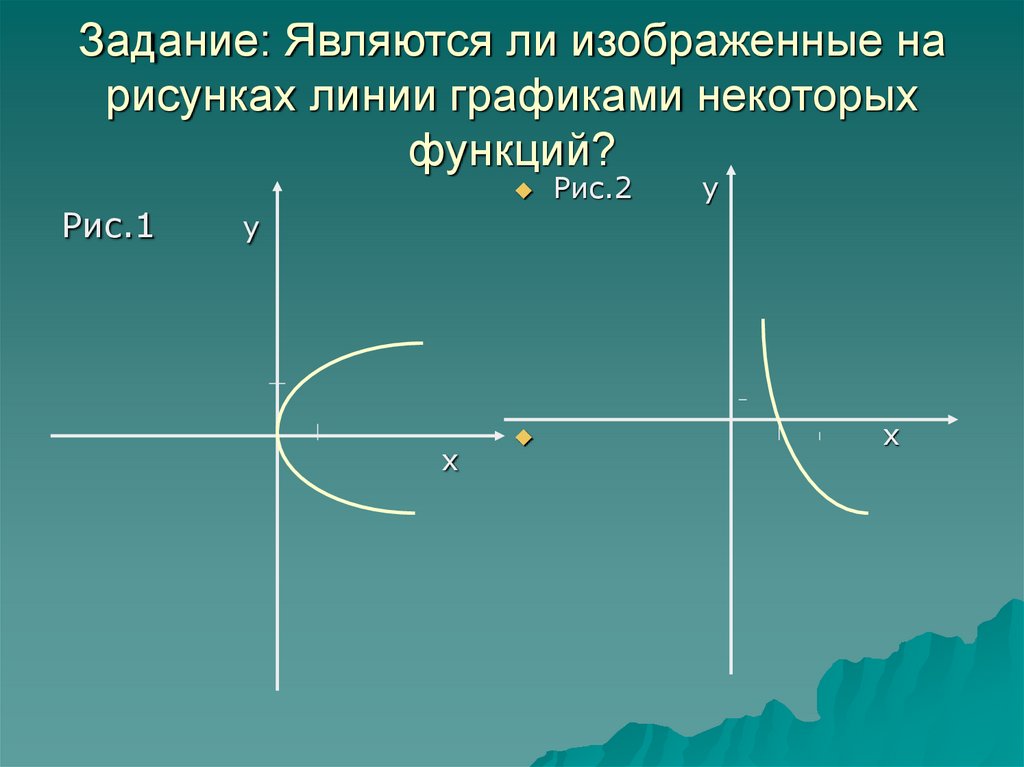
10. Задание: Являются ли изображенные на рисунках линии графиками некоторых функций?

Рис.1
Рис.2
у
у
х
х

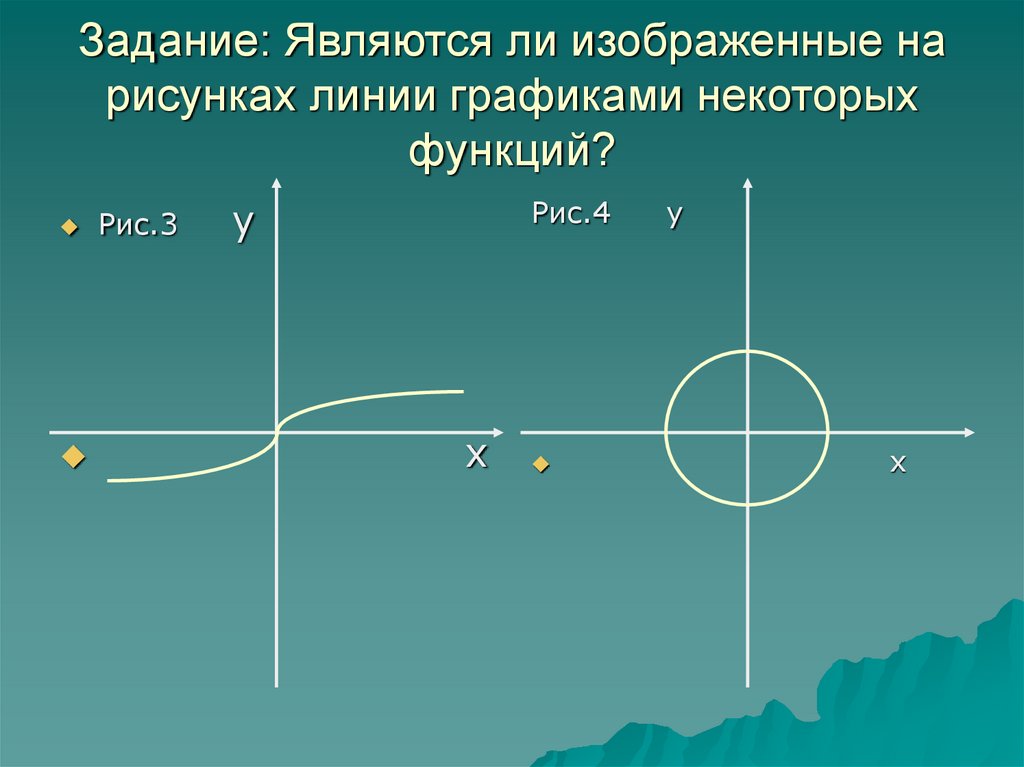
11. Задание: Являются ли изображенные на рисунках линии графиками некоторых функций?

Рис.3
у
Рис.4
х
у
х

12. Область определения функции

Областью
определения
функции называется
множество всех
значений независимой
переменной х, т.е.
аргумента.

13. Задание: найти область определения функции по ее графику

1) D(у) 4; 1 1;
2)
D( у) ;0 0;2
3)
D(у) 4; 1 1;
4)
D( у) 4;
у
-1
0
х

14. Задание: найти область определения функции по ее графику

1)
D( у) ;
2)
D(у) ;0 0;
3)
D(у) ;2 2;
4)
D( у) ;2
у
2
0
х

15. Задание: найти область определения функции по ее графику

1)
D(у) ;0 2;
у
2) D(у) ; 1 0;
3)
D( у) 0;2 2;
4)
D( у) 0;
0
-1
2
х

16. Условия существования функции

№
1
2
3
4
5
Формула
g ( x)
f ( x)
f ( x) 0
y 2n f ( x)
1
y
2n f ( x)
y log a f ( x)
f ( x) 0
y log g ( x) b
y
условия
f ( x) 0
f ( x) 0
6
y log g ( x) f ( x)
g ( x) 0;
g ( x ) 1.
g ( x) 0;
g ( x) 1;
f ( x ) 0.
7
8
9
y f ( x) p , где p нецелое, p 0
f ( x) 0 ;
y f ( x) p , где p нецелое, p 0
y tgt
f ( x) 0
10
y ctgt
n, гдеn Z
2
t n, гдеn Z
t

17. Найти область определения функции.

1.
y log 5 2 x 8
2.
y x 3x 4
6
2
y 6 3x
0 , 3
3.
4.
5
y tg 2 x
2

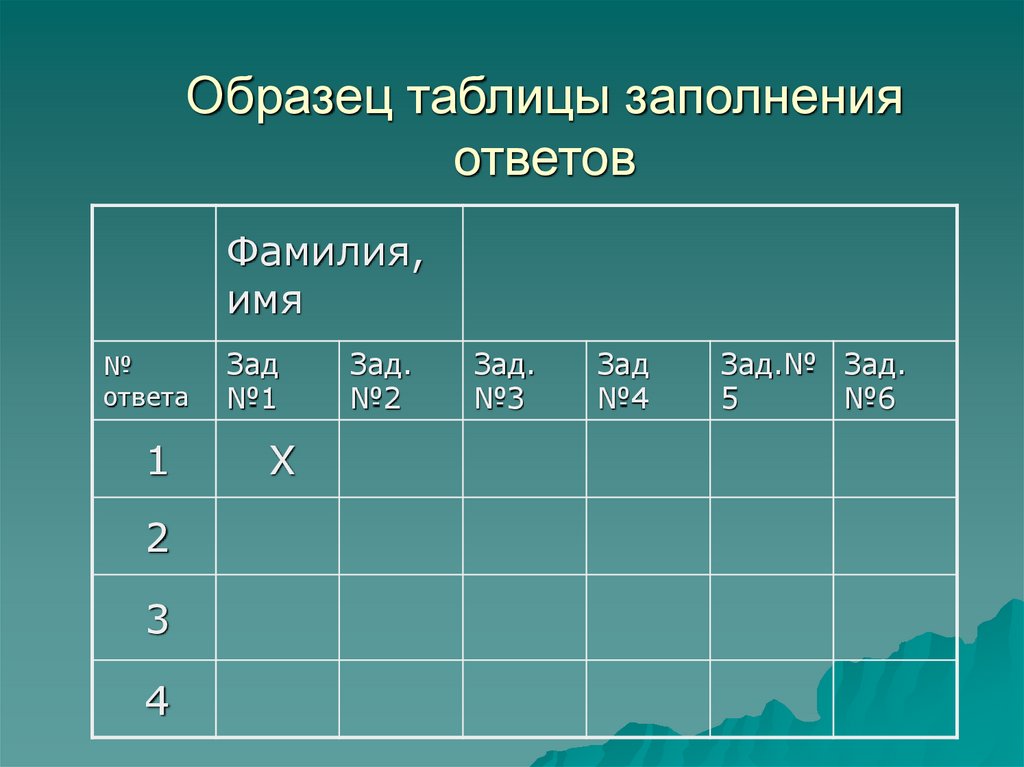
18. Образец таблицы заполнения ответов

Фамилия,
имя
№
ответа
1
2
3
4
Зад
№1
X
Зад.
№2
Зад.
№3
Зад
№4
Зад.№ Зад.
5
№6

19. Решите самостоятельно

Вариант I.
x
.
2x 6
2) ;3 3;
4) ;
1. Найти область определения функции: y
Ответы: 1) ;0 0;3 3;
3) ;0 0;
2. Найти область определения функции: y x 2 9 .
Ответы: 1) ; 3 3;
2) ;
3) ; 3 3;
4) 3;
3. Найти область определения функции: y log 2 2 x 7
Ответы: 1) 0;
2) ;3,5
3) 3,5;
4) 3,5;
4. Найти область определения функции: y 4 x 2 2
1
Ответы: 1) 0; 2) 0,5; 3) ; 4) ;
2
2
5. Найти область определения функции: y x x 6
Ответы: 1) ; 2 3; 2) 2;3
3) ; 2 3;
4) ; 3 2;
1
x
6. Найти область определения функции: y 2 tg sin x
Ответы: 1) x
n , где n Z
2
3) x 4 n , где n Z
4
2) x n , где n Z
4) x 2 4 n , где n Z

20. Решите самостоятельно

Вариант II
x
.
4x 8
Ответы: 1) ; 2) ; 2 2;0 0;
3) ;0 0;
4) ; 2 2;
1. Найти область определения функции: y
2. Найти область определения функции: y 4 x 2 .
Ответы: 1) ;
2) 0;
3) 2;
4) ; 2 2;
3. Найти область определения функции: y log 1 8 5 x
Ответы: 1) 0;
4) 1,6;
2) ;1,6
2
3) ;1,6
4. Найти область определения функции: y 0,2 x 4 5
Ответы: 1) 20; 2) 0; 3) 20; 4) ;20
5. Найти область определения функции: y x 2 4 x 5
Ответы: 1) ; 1 5;
2) 1;5
3) ; 1 5;
4) ; 5 1;
3
1
2
6. Найти область определения функции: y ctg 2 x cos x
Ответы: 1) x
n
, где n Z
2
n
3) x
, где n Z
4
2
2) x n , где n Z
4) x 2 n , где n Z