Похожие презентации:
Приближенное вычисление определенных интегралов
1.
ПРИБЛИЖЕННОЕВЫЧИСЛЕНИЕ
ОПРЕДЕЛЕННЫХ
ИНТЕГРАЛОВ
Марданова Гульсина Насиховна, учитель
информатики СОШ №9 г. Нижнекамска
2.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯКакая
фигура называется
криволинейной трапецией?
Как вводится равномерное
разбиение отрезка?
Объясните, что такое интеграл.
3.
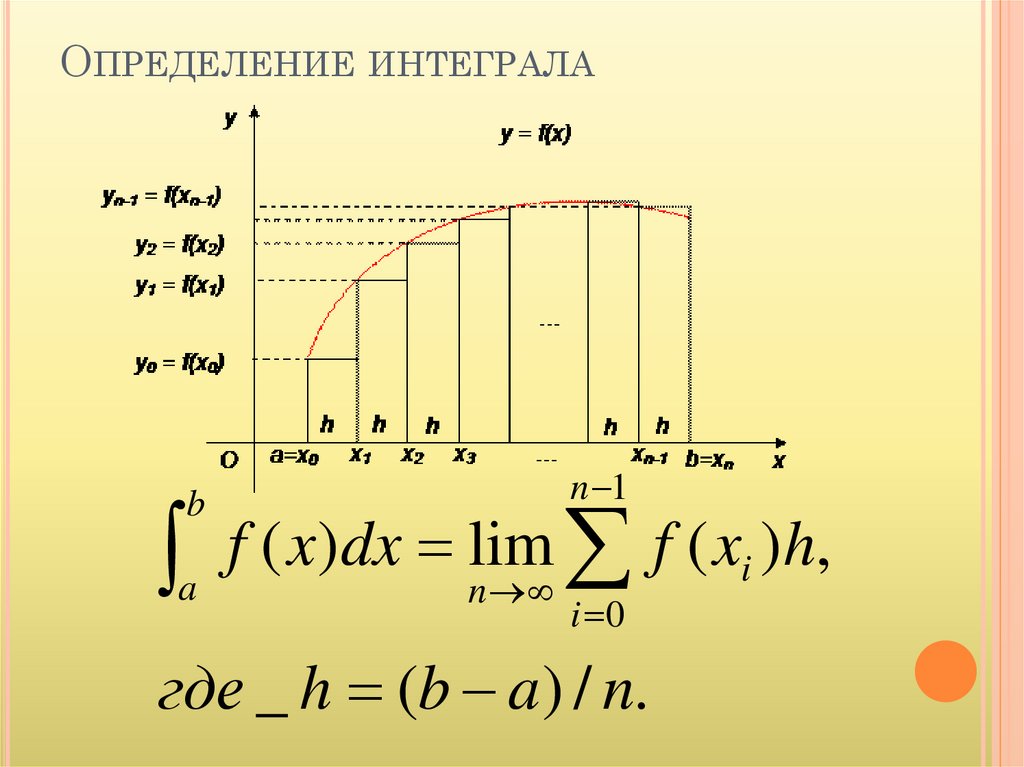
ОПРЕДЕЛЕНИЕ ИНТЕГРАЛАb
a
n 1
f ( x)dx lim f ( xi )h,
n
i 0
где _ h (b a ) / n.
4.
СПОСОБЫ ВЫЧИСЛЕНИЙ, ОСНОВАННЫЕ НАЗАМЕНЕ ИНТЕГРАЛА КОНЕЧНОЙ СУММОЙ
Формула
левых прямоугольников
Формула правых
прямоугольников
Формула центральных
прямоугольников
Формула трапеций
5.
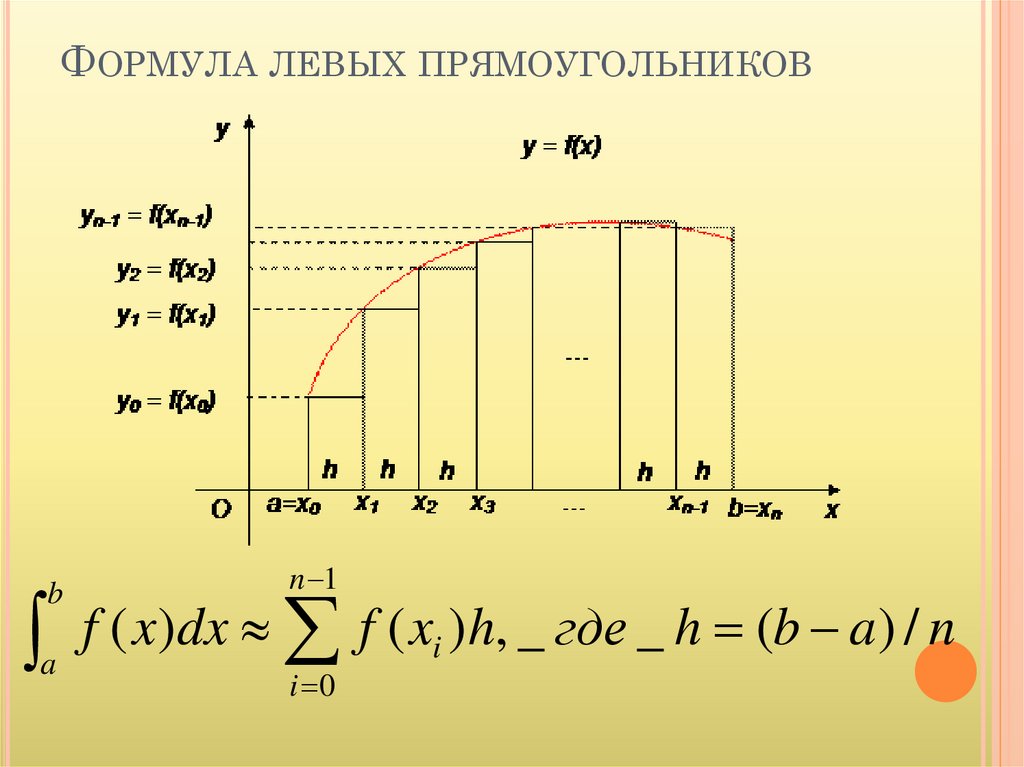
ФОРМУЛА ЛЕВЫХ ПРЯМОУГОЛЬНИКОВb
a
n 1
f ( x)dx f ( xi )h, _ где _ h (b a ) / n
i 0
6.
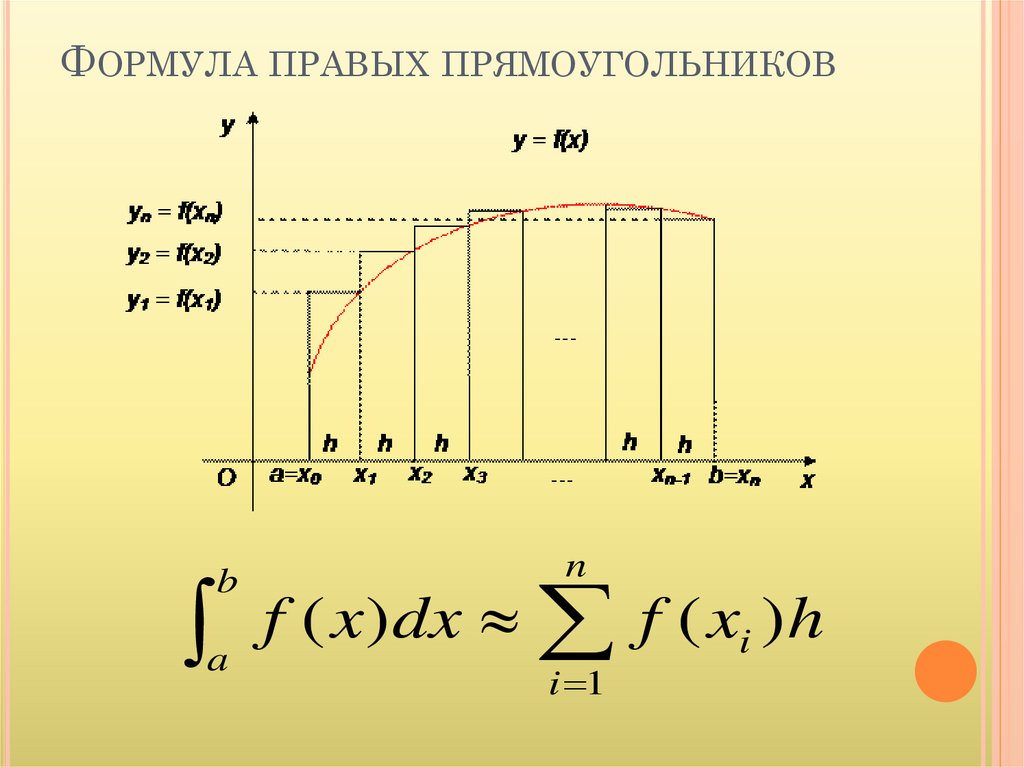
ФОРМУЛА ПРАВЫХ ПРЯМОУГОЛЬНИКОВb
a
n
f ( x ) dx f ( xi ) h
i 1
7.
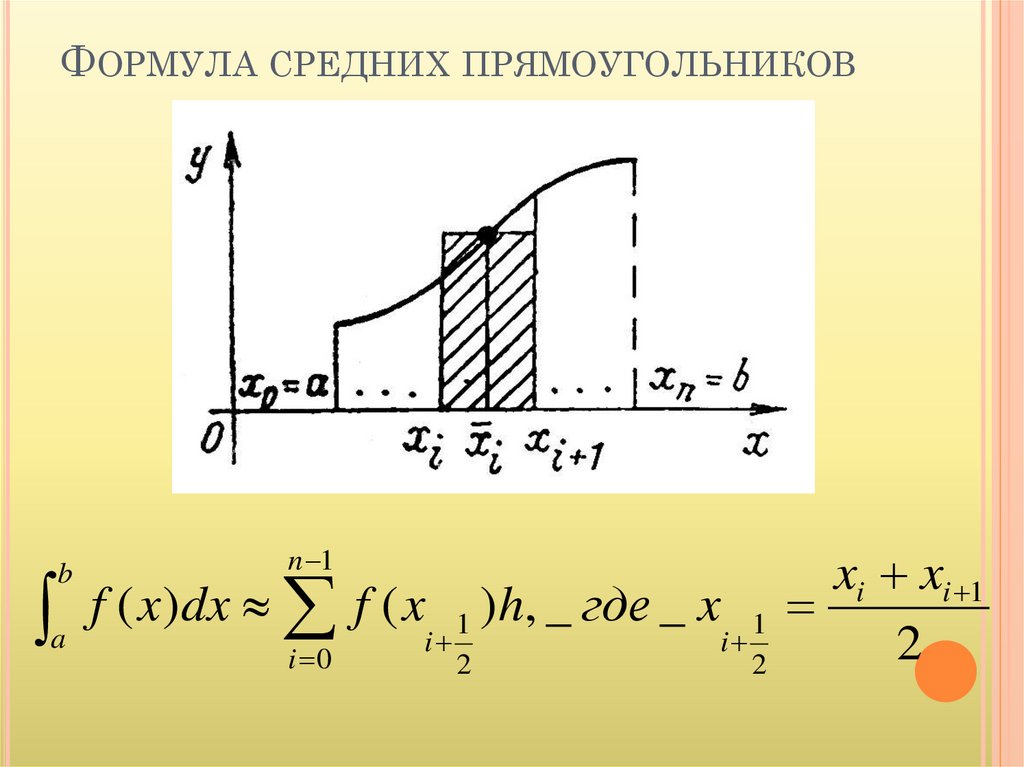
ФОРМУЛА СРЕДНИХ ПРЯМОУГОЛЬНИКОВb
a
n 1
f ( x)dx f ( x
i 0
1
i
2
)h, _ где _ x
i
1
2
xi xi 1
2
8.
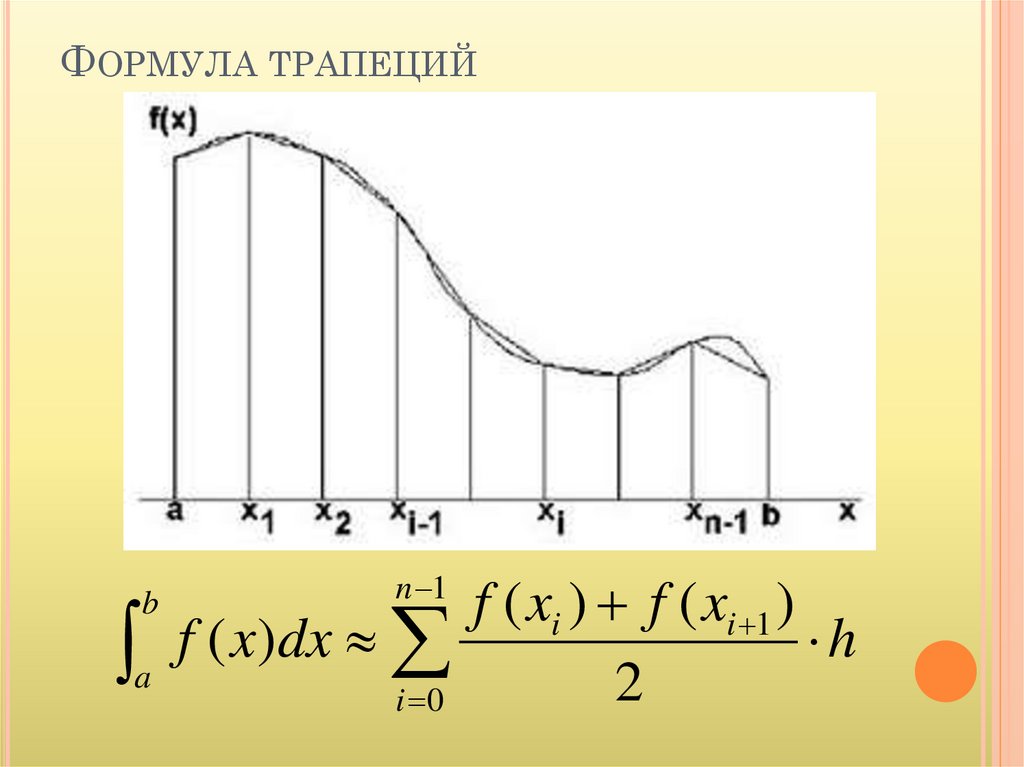
ФОРМУЛА ТРАПЕЦИЙb
a
n 1
f ( x)dx
i 0
f ( xi ) f ( xi 1 )
h
2
9.
ЗАДАЧАВычислить приближенно определенный
интеграл при n=10, n=20, n=30 в электронных
таблицах MS Excel.
3
0
4 x dx
2
10.
РЕШЕНИЕa=0,
b=3
n=10, 20, 30
h=(b-a)/n
f ( x) 4 x
2
11.
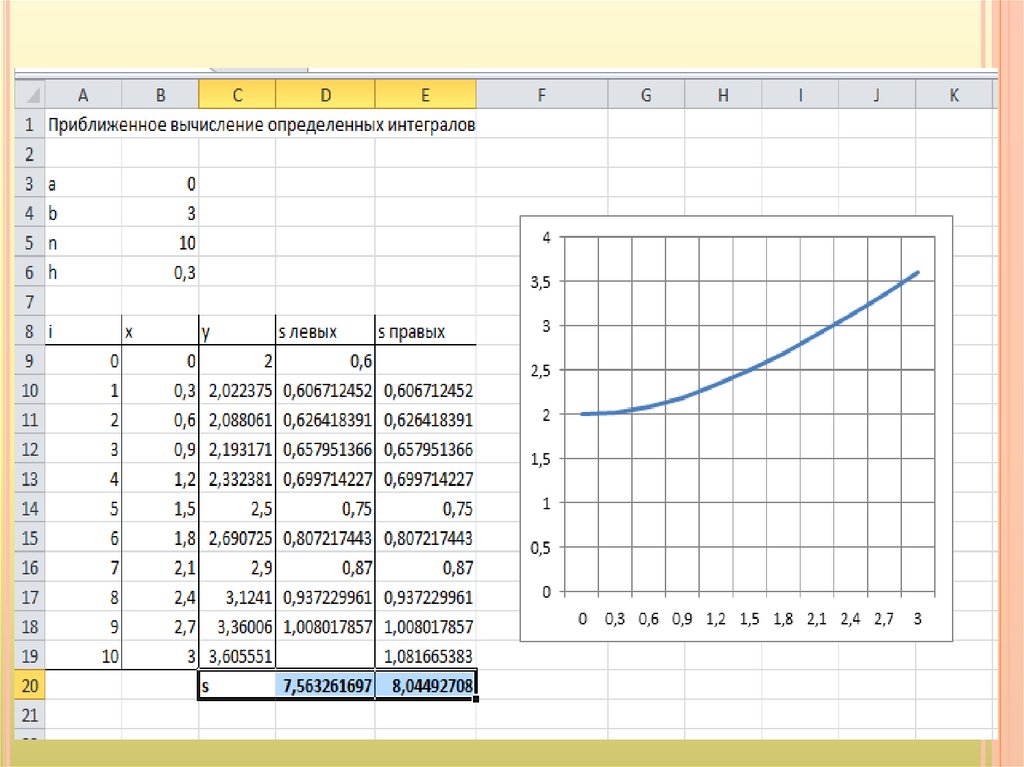
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫЗадать
начальные значения a, b, n, h.
Задать номера узлов i.
Задать значения х с вычисленным
шагом h.
Вычислить значения y по формуле.
Построить график функции.
Найти площади прямоугольников Si.
Найти сумму площадей
прямоугольников.
Записать результаты.
12.
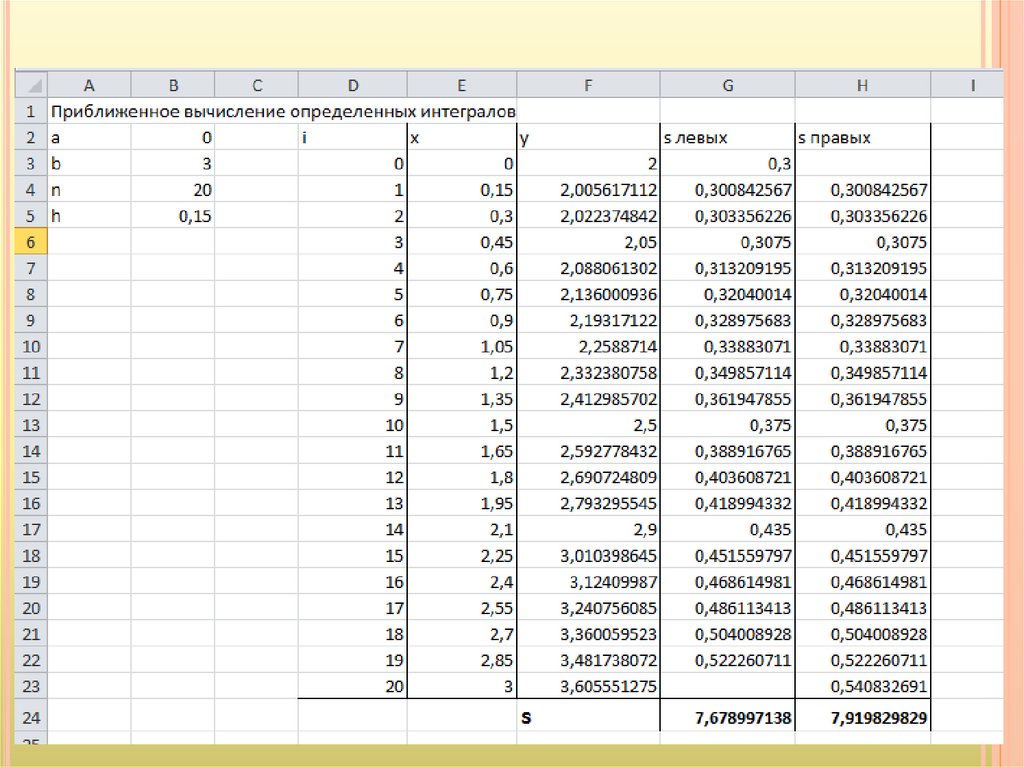
13.
14.
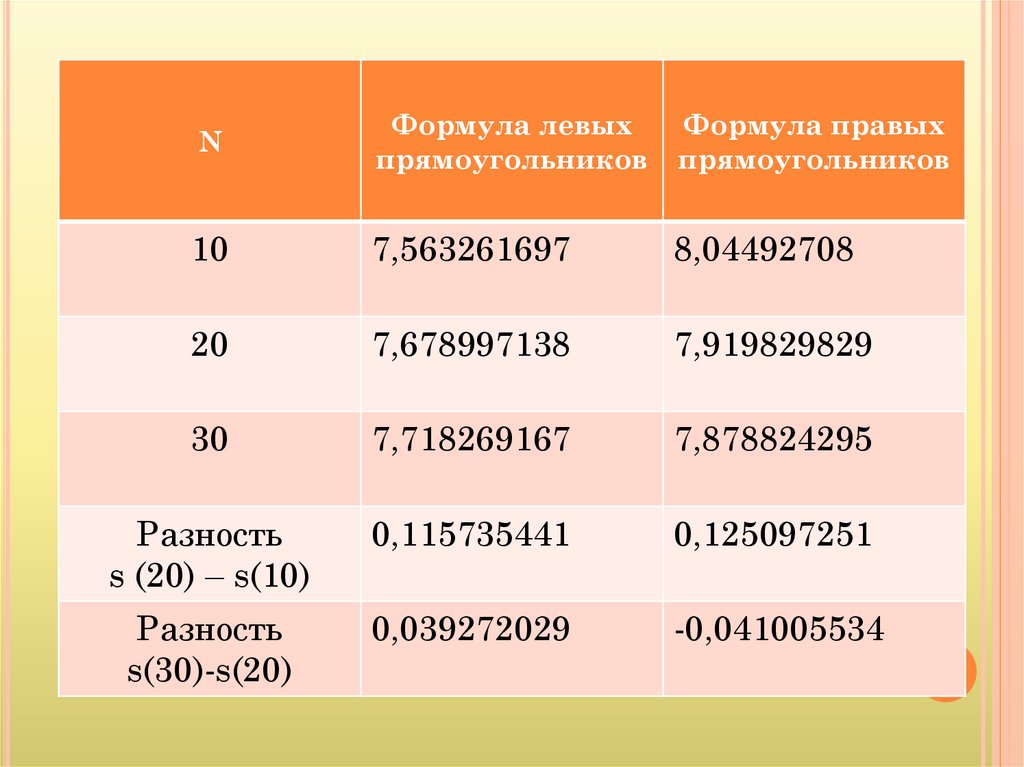
NФормула левых
прямоугольников
Формула правых
прямоугольников
10
7,563261697
8,04492708
20
7,678997138
7,919829829
30
7,718269167
7,878824295
Разность
s (20) – s(10)
0,115735441
0,125097251
Разность
s(30)-s(20)
0,039272029
-0,041005534
15.
ТОЧНОСТЬ ВЫЧИСЛЕНИЙЗадаем начальное значение n.
Для него рассчитываем значение суммы S1.
Увеличиваем n в два раза.
Для данного n вычисляем сумму S2.
Процесс увеличения n, а значит и вычислений
останавливаем , если достигнута точность
вычислений:
s1 s 2
16.
ЗАДАЧАСоставить
программу для
приближенного вычисления
определенного интеграла с точностью
0.001
3
0
4 x dx
2
17.
РЕШЕНИЕa=0,
b=3
eps=0.001
n=10
h=(b-a)/n
f ( x) 4 x
2
18.
ФОРМУЛА ЛЕВЫХ ПРЯМОУГОЛЬНИКОВb
a
n 1
f ( x)dx f ( xi )h, _ где _ h (b a) / n
i 0
ФОРМУЛА ПРАВЫХ ПРЯМОУГОЛЬНИКОВ
b
a
n
f ( x) dx f ( xi )h
i 1
19.
ПРОГРАММА МЕТОД ЛЕВЫХ ПРЯМОУГОЛЬНИКОВProgram SumL;
var a,b,h,s,s1,x,eps: real;
i,n: integer;
function f(z: real): real;
begin
f:= sqrt(4+z*z);
end;
20.
begina:=0; b:=3; eps:=0.001;
n:=5; s1:=15;
repeat
s:=s1; s1:=0;
n:=n*2; h:=(b-a)/n;
21.
for i:=0 to n-1 dobegin
x:=a+i*h;
s1:=s1+f(x)*h;
end;
until abs(s-s1)<eps;
writeln(‘s=‘,s);
End.
22.
ФОРМУЛА СРЕДНИХ ПРЯМОУГОЛЬНИКОВb
a
n 1
f ( x)dx f ( x
i 0
1
i
2
)h, _ где _ x
1
i
2
xi xi 1
2
ФОРМУЛА ТРАПЕЦИЙ
b
a
n 1
f ( x)dx
i 0
f ( xi ) f ( xi 1 )
h
2
23.
ПРОГРАММА МЕТОД СРЕДНИХ ПРЯМОУГОЛЬНИКОВProgram SumS;
var a,b,h,s,s1,x,eps: real;
i,n: integer;
function f(z: real): real;
begin
f:= sqrt(4+z*z);
end;
24.
begina:=0; b:=3; eps:=0.001;
n:=5; s1:=15;
repeat
s:=s1; s1:=0;
n:=n*2; h:=(b-a)/n;
25.
for i:=0 to n-1 dobegin
x:=a+i*h+h/2;
s1:=s1+f(x)*h;
end;
until abs(s-s1)<eps;
writeln(‘s=‘,s);
End.
26.
ПРОГРАММА МЕТОД ТРАПЕЦИЙProgram SumT;
var a,b,h,s,s1,x,x1,eps: real;
i,n: integer;
function f(z: real): real;
begin
f:= sqrt(4+z*z);
end;
27.
begina:=0; b:=3; eps:=0.001;
n:=5; s1:=15;
repeat
s:=s1; s1:=0;
n:=n*2; h:=(b-a)/n;
28.
for i:=0 to n-1 dobegin
x:=a+i*h;
x1:=a+(i+1)*h;
s1:=s1+(f(x)+f(x1))/2*h;
end;
until abs(s-s1)<eps;
writeln(‘s=‘,s);
End.
29.
ВЫЧИСЛИТЬ ПРИБЛИЖЕННО ИНТЕГРАЛЫ6
1)
0
dx
1 x
4
10
2) ( x 5) (10 x ) dx
2
0
3)
2
cos x
dx
x




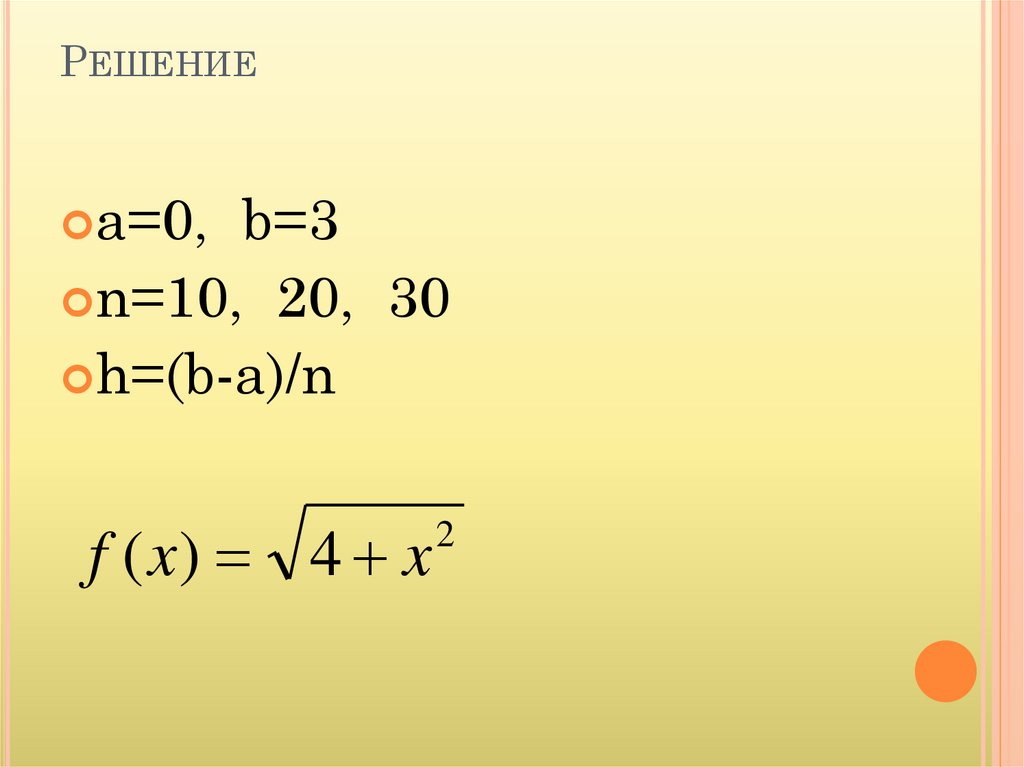



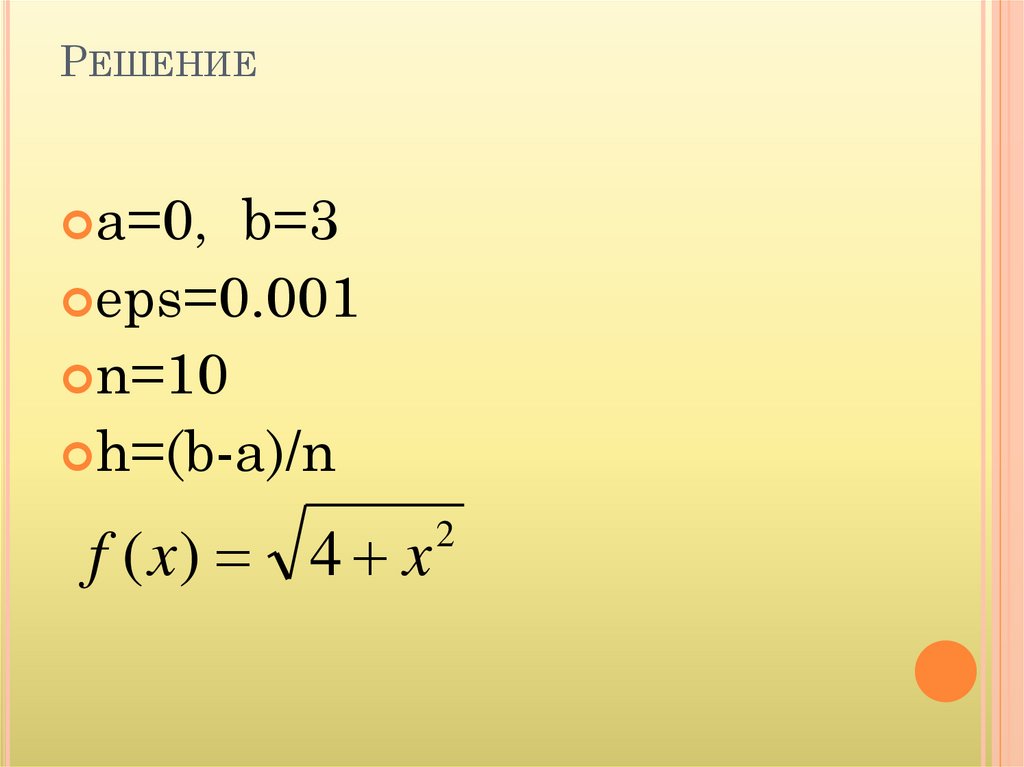
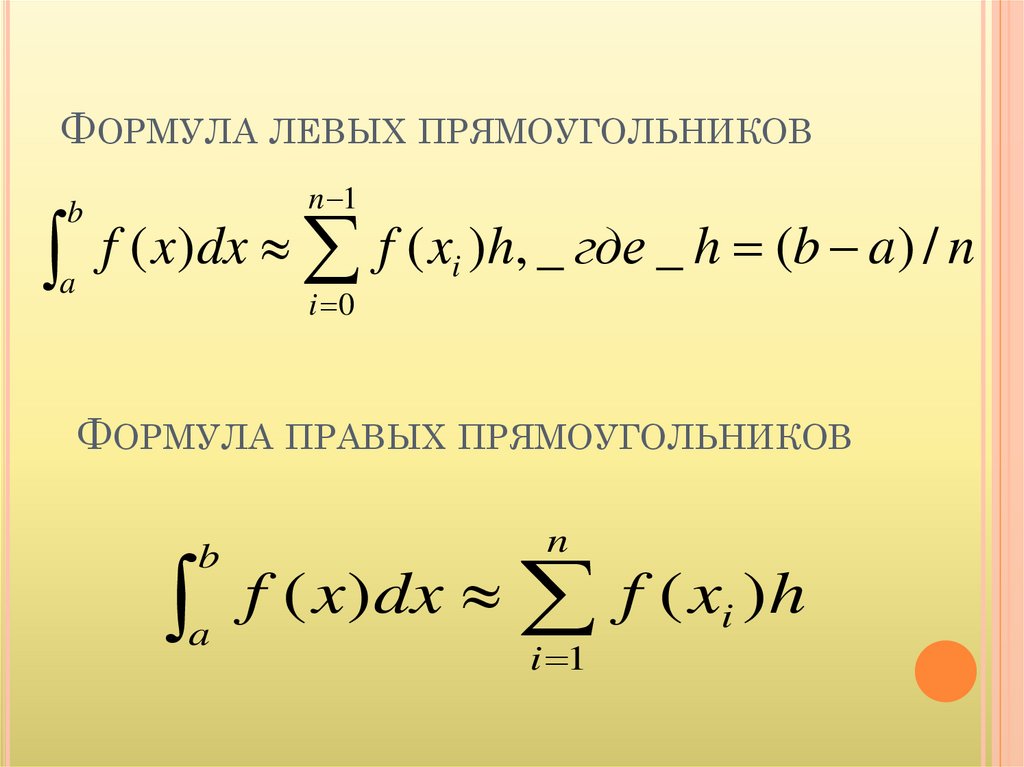


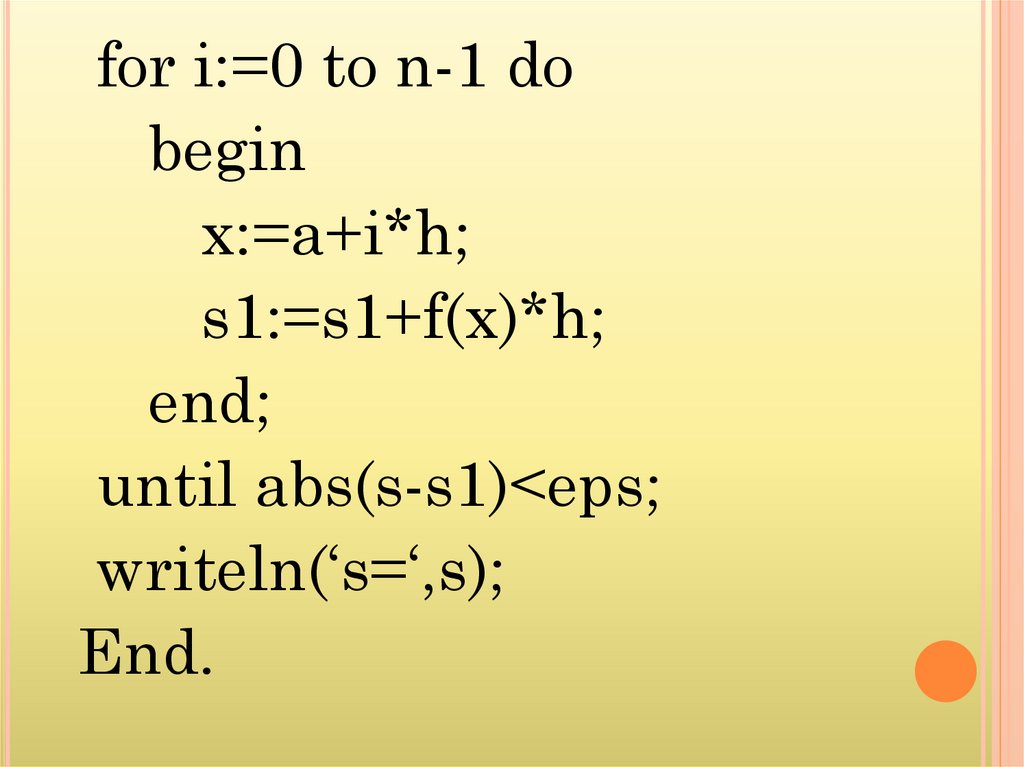



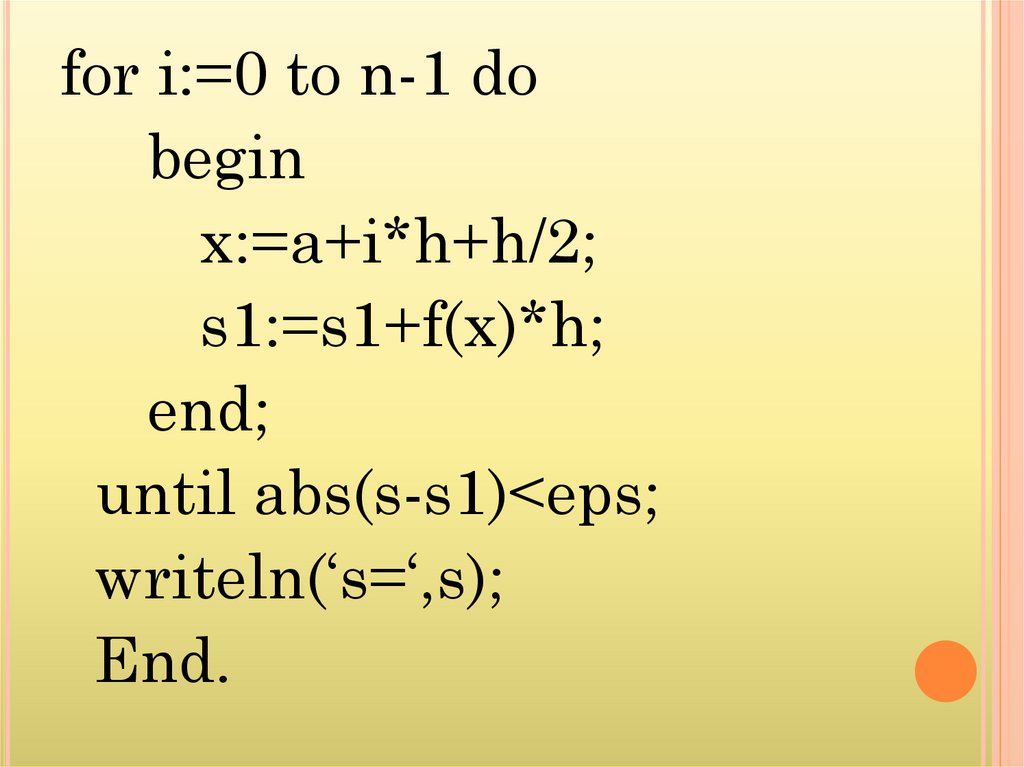




 Информатика
Информатика








