Похожие презентации:
Математический аппарат квантовой механики
1.
Русакова Н.П.Квантовая механика
и квантовая химия
Лекция № 2
Математический аппарат
квантовой механики
Часть первая
3 курс ХТФ
2. Квантовая модель атома Шредингера
2Русакова Н.П.
Квантовая механика и квантовая химия
Квантовая модель атома Шредингера
• Описал движение электрона-волны в пространстве с
помощью математического уравнения – волновой функции
–ψ
• - орбиталь – это пространство вокруг ядра, в котором
можно обнаружить заселивший
её электрон с вероятностью 95%
• Вероятность – из принципа неопределённостей Гейзенберга (нет точной
траектории – импульс и
координата одновременно
с максимально заданной
точностью неизмеримы).
2
3. Квантовая модель атома Шредингера
3Русакова Н.П.
Квантовая механика и квантовая химия
Квантовая модель атома Шредингера
• Существование уровней, орбиталей
различной формы
3
4. Квантовая теория атома -
4Русакова Н.П.
Квантовая механика и квантовая химия
Квантовая теория атома - это теоретическая модель
сложного природного явления –
атома. Позволяет предсказывать
многие (в том числе и неоткрытые)
свойства различных элементов
• Молекула – это система атомных ядер и
электронов
4
5.
Русакова Н.П.5
Квантовая механика и квантовая химия
Понятие оператора
Квантовомеханическое представление атома –
система ядра атома химического элемента и
движущихся в его поле электронов. Ядра
неподвижны по отношению к движению
электронов, их масса много больше.
Свойства атомов определяются характером
движения электронов в нём.
Движение электронов описывается волновой
электронной функцией - ψе.
Точными решениями ψе являются средние
значения операторов динамических физических
свойств
6.
Русакова Н.П.Квантовая механика и квантовая химия
Понятие оператора
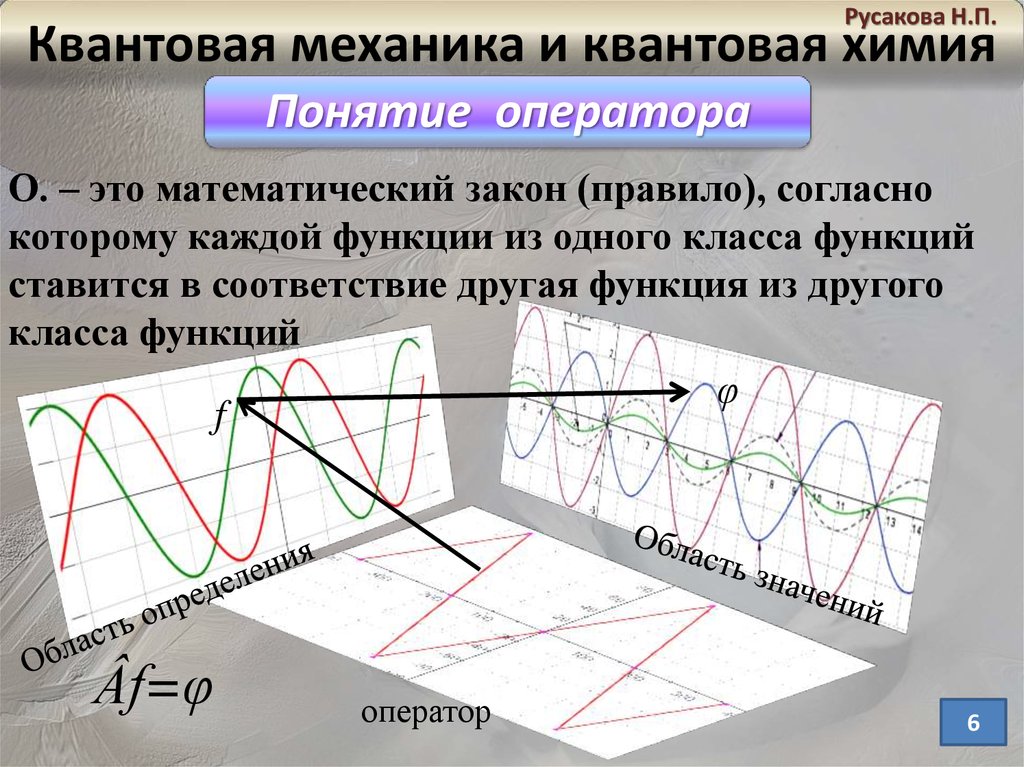
О. – это математический закон (правило), согласно
которому каждой функции из одного класса функций
ставится в соответствие другая функция из другого
класса функций
φ
f
Âf=φ
оператор
6
7.
Русакова Н.П.Квантовая механика и квантовая химия
Понятие оператора
Оператор – действие - функция, областью определения и
областью значений которой является множество числовых
функций.
Âf=φ
О. – задан, если указано множество функций, на которые
он действует
Âf= аf=φ
Это множество – область определения О., а О. – называется определённым (оператор Â переводит функцию f в φ )
В кв. мех – действуя О. на волновую функцию получаем
собственные значения и собственную функцию оператора
Âψ=aψ
7
8.
Русакова Н.П.Квантовая механика и квантовая химия
Свойства оператора
1. Произведением двух операторов Â и B называется оператор Â ·B ,
действие которого на функцию сводится к последовательному
действию сначала оператора B , а потом оператора Â на результат
действия B:
Изменим порядок действия этих операторов:
операторы нельзя переставлять местами:
8
9.
Русакова Н.П.Квантовая механика и квантовая химия
Свойства оператора
2. Суммой двух операторов Â и B называется оператор Â ± B ,
который действует на функцию f следующим образом:
Если операторы Â и B равны:
Операторы Â и B определены в одной и той же области и одинаково
действуют на функцию, т.е. переводят её в одну и ту же функцию.
Если действие оператора записывается, как Âf = 0, то Â = 0:
оператор Â переводит функцию в тождественный нуль
9
10.
Русакова Н.П.Квантовая механика и квантовая химия
Свойства оператора
3. Коммутация операторов. Выражение вида:
называется коммутатором операторов Â и B . Если [Â, B]=0, то
говорят, что операторы коммутируют. В противном случае
операторы не коммутируют.
В силу действия в кв. механике принципа неопределённостей
Гейзенберга одним из условий, накладываемых на операторы
разных динамических свойств (н.п.: импульс и координата),
является отсутствие их коммутации:
10
11.
Русакова Н.П.Квантовая механика и квантовая химия
Векторные операторы:
Набла , который определён на дифференцируемых функциях
трёх переменных:
где k j,i, – единичные, взаимно ортогональные векторы
Произведение двух векторных операторов даёт оператор
Лапласа. Он определён на функциях трёх переменных,
имеющих вторые частные производные
11
12.
Русакова Н.П.Квантовая механика и квантовая химия
оператора Â
12
13.
Русакова Н.П.Квантовая механика и квантовая химия
13
14.
Русакова Н.П.Квантовая механика и квантовая химия
14
15.
Русакова Н.П.Квантовая механика и квантовая химия
Вывод оператора импульса и координаты
Оператор импульса определяется через операторы его проекций
на оси:
Оператор координаты – координата. При действии им на любую
функцию – функция умножается на вектор, который определяется
координатами x, y, z:
xf x f
r ( x, y , z )
rf rf
yf y f
zf z f
15
16.
Русакова Н.П.Квантовая механика и квантовая химия
Вывод оператора кинетической энергии
2
2
2 2
m
p
m
,
p
m
Классическая формула: T
для импульса
2
16
17.
Русакова Н.П.Квантовая механика и квантовая химия
17
18.
Русакова Н.П.Квантовая механика и квантовая химия
Ограничения на операторы, соответствующие
реальным физическим величинам.
Линейность
Эрмитовость
где С1 и С2 – числа, а f1 и f2 –
функции, на которых определён
оператор Â
оператор Â, определённый на
функциях f1(x), f2(x) – самосопряжённый или эрмитовый
При действии оператором на
сумму двух, не равных функций,
получаем сумму действий на
каждую из функций этим
оператором
Интеграл первой функции, взятый по
элементу второй, на которую действует
оператор, равен интегралу второй
функции, взятому по элементу первой
функции, на которую действует этот
оператор
18
19.
Русакова Н.П.Квантовая механика и квантовая химия
Спасибо за внимание!
19
20. Задание на усвоение
Фамилия, Имя1. Дайте определение оператора
2. Перечислите ограничения, накладываемые на
операторы физических величин в квантовой
механике
3. Перечислите основные операторы квантовой
механики
4. Выражение для коммутатора двух
операторов
20



















 Химия
Химия