Похожие презентации:
Применение определенного интеграла к вычислению площадей плоских фигур
1.
2.
Понятиекриволинейной трапеции.
Определение площади фигуры при ее
различном расположении.
Решение типовых задач.
3.
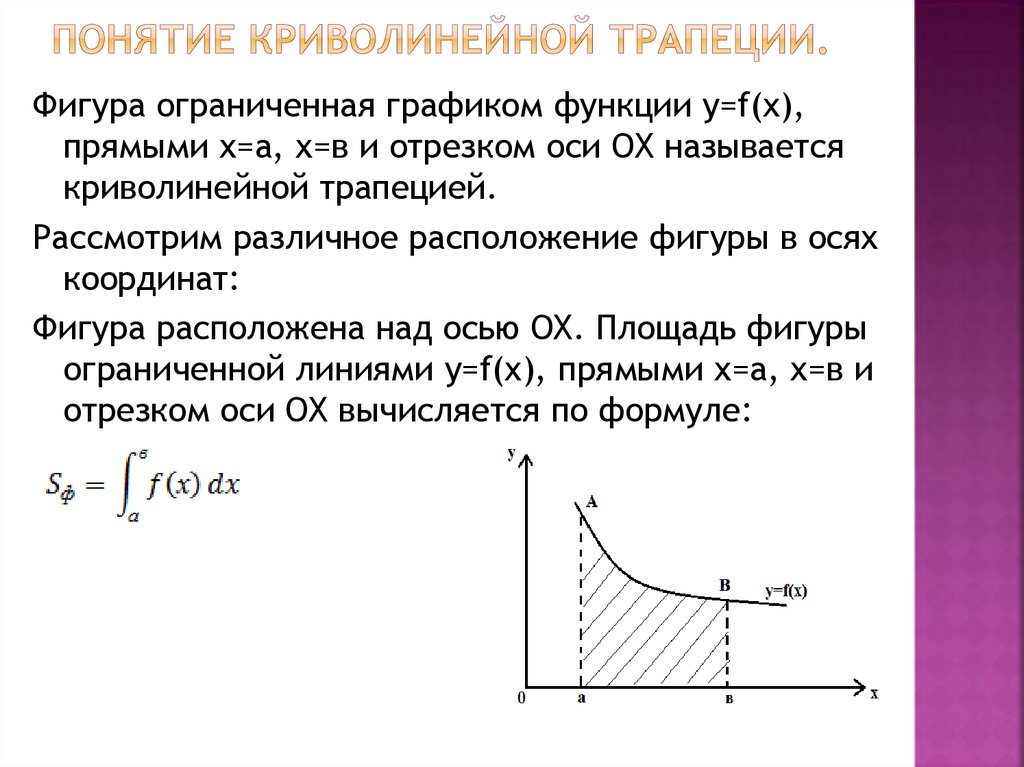
Фигура ограниченная графиком функции у=f(х),прямыми х=а, х=в и отрезком оси ОХ называется
криволинейной трапецией.
Рассмотрим различное расположение фигуры в осях
координат:
Фигура расположена над осью ОХ. Площадь фигуры
ограниченной линиями у=f(х), прямыми х=а, х=в и
отрезком оси ОХ вычисляется по формуле:
4.
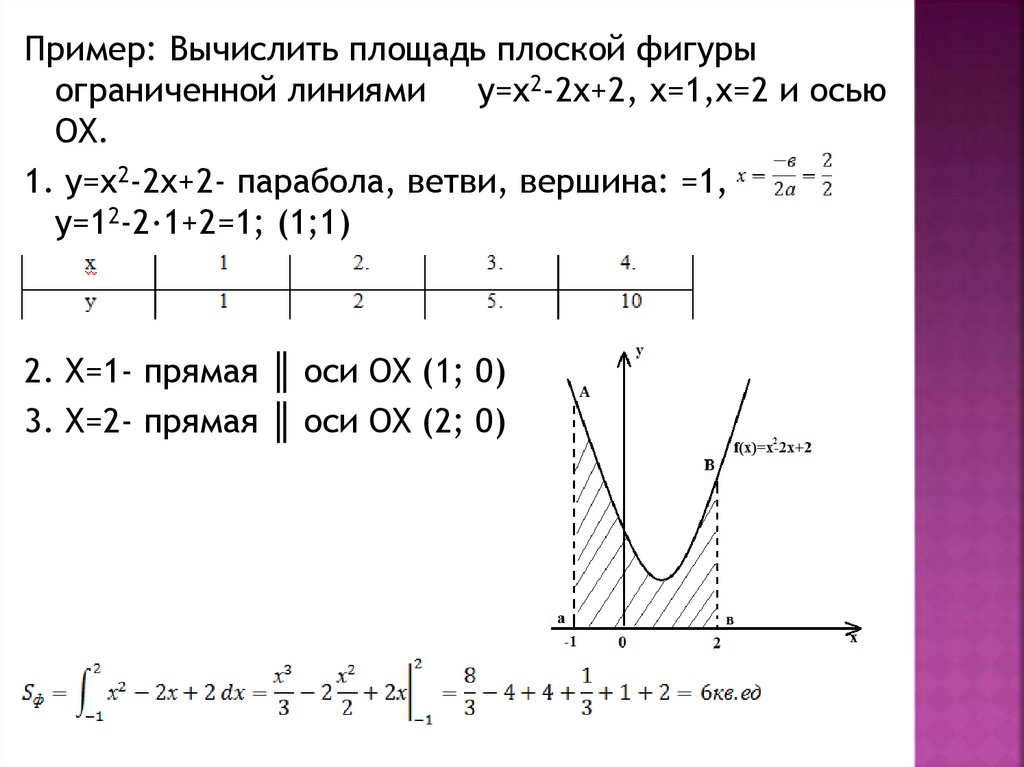
Пример: Вычислить площадь плоской фигурыограниченной линиями
у=х2-2х+2, х=1,х=2 и осью
ОХ.
1. у=х2-2х+2- парабола, ветви, вершина: =1,
у=12-2∙1+2=1; (1;1)
2. Х=1- прямая ║ оси ОХ (1; 0)
3. Х=2- прямая ║ оси ОХ (2; 0)
5.
Фигура расположена под осью ОХ. Пусть функцияу=f(х), неположительная непрерывная функция. В
этом случае график расположен под осью ОХ.
Рассмотрев вспомогательную функцию
у= - f(х)
получим площадь фигуры аА1В1в, ограниченной
графиком функции у= - f(х) . Так как фигуры
равны, то равны и их площади.
6.
Пример: Вычислить площадь фигуры ограниченнойлиниями
, х= - 1 и осью ОХ.
х= - 1 и осью ОХ.
1.
- кубическая парабола, 1 и 3 четверть
2. х= -1- прямая ║ оси ОХ (-1; 0)
3. у=0 – ось ОХ
7.
3. Фигура не является криволинейной трапецией.Рассмотрим фигуру ограниченную отрезками прямых
х=а, х=в и графиками функций у=f(x) и у=g(x). Эту
фигуру
можно рассматривать как разность криволинейных
трапеций аАВв и аМNв, поэтому формула для
вычисления площади примет вид:
8.
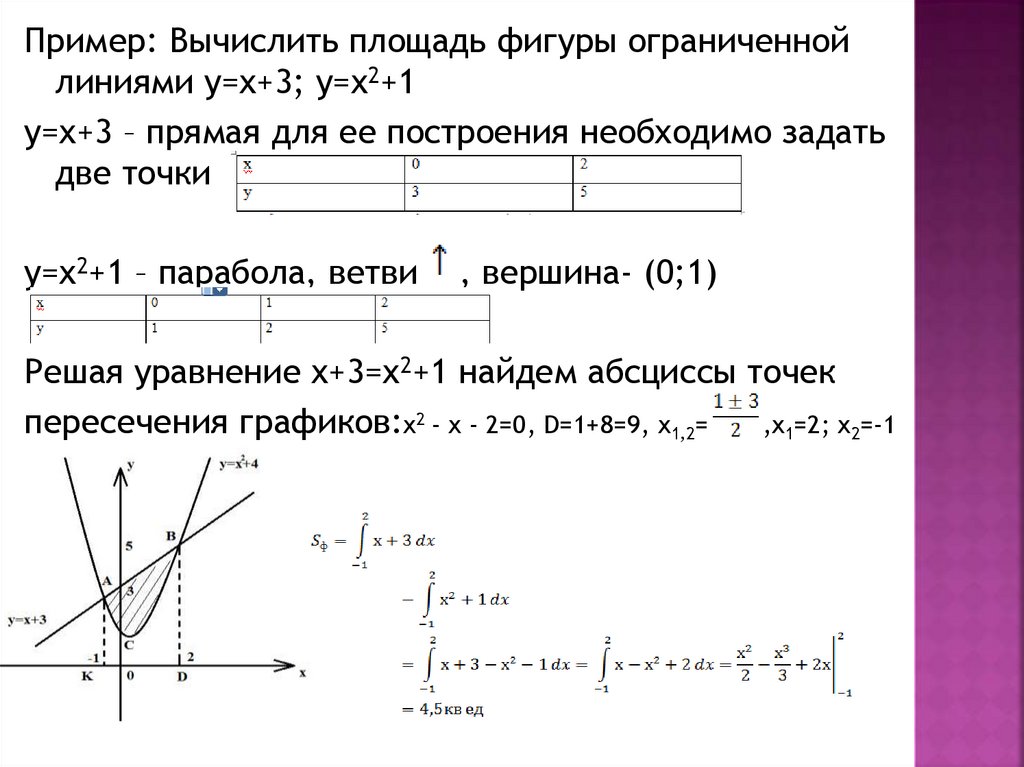
Пример: Вычислить площадь фигуры ограниченнойлиниями у=х+3; у=х2+1
у=х+3 – прямая для ее построения необходимо задать
две точки
у=х2+1 – парабола, ветви
, вершина- (0;1)
Решая уравнение х+3=х2+1 найдем абсциссы точек
пересечения графиков:х2 - х - 2=0, D=1+8=9, х1,2=
,х1=2; х2=-1
9.
4. Если требуется вычислить площадь плоскойфигуры более сложного вида, то стараются
выразить искомую площадь в виде суммы и
разности площадей криволинейных трапеций
входящих в ее состав.
10.
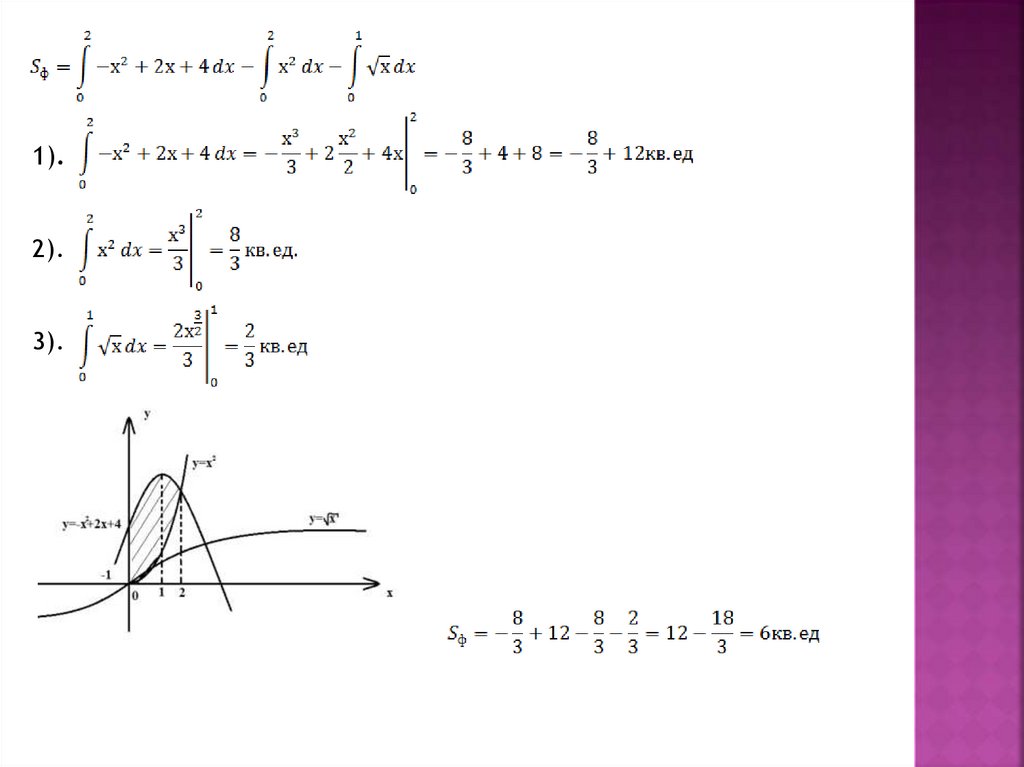
Пример: Вычислить площадь фигуры ограниченнойлиниями:
1).
2). У=х2 - парабола, ветви , вершина: (0;0)
3). У= - х2+2х+4 – парабола, ветви
1+2+4=5; (1;5)
, вершина ; у=-
11.
1).2).
3).
12.
Пример 1. Вычислить площадь фигуры,x 2 y 4 0,
y 0, x 3, x 2
1
ограниченной линиями 2 y x 4, y 2 x 2
Решение. Выполним построение фигуры.
Выразим из первого уравнения у через x.
Прямую строим по двум точкам (4;0) и (0;2)
1
1
S x 2 dx x 2 2 x 1 4 4 1 9 6 1 4 9 6 11 1 (кв. ед.)
2
4
4
3
4
4
3
4
4
2
13.
Пример 2. Вычислить площадь фигуры,ограниченной линиями x 2 y 4 0, x y 5 0, y 0
Решение.
Выполним построение фигуры. Построим прямую
1
x 2 y 4 0, 2 y x 4, y 2 x 2, x 0, y 2, A (0; 2). y 0, x 4, B ( 4; 0)
Построим прямую
x y 5 0, y x 5, x 0, y 5, C (0; 5).
y 0, x 5, D (0; 5).
Найдем точку пересечения прямых, решив систему
уравнений
1
3
1
y x 2
x 3 x 2, y 3
x
2
x
5
2
2
2
y x 5
M (2; 3)
14.
Для вычисления искомой площади разобьемтреугольник AMC на два треугольника
AMN и
NMC.
S S AMN S NMC
S AMN
2
1
1
1
1 2
x 2 dx x 2 x 4 4 16 8 1 4 4 8 9(кв.ед.)
2
4
4
4 4
4
S NMC
5
x2
25 25 4 10
( x 5)dx 5 x
12,5 25 2 10 4,5(кв.ед)
2
2
2
2
2
2
5
S 9 4,5 13,5 (кв.ед.)










 Математика
Математика








