Похожие презентации:
Применение интеграла к вычислению площадей различных фигур
1. Применение интеграла к вычислению площадей различных фигур
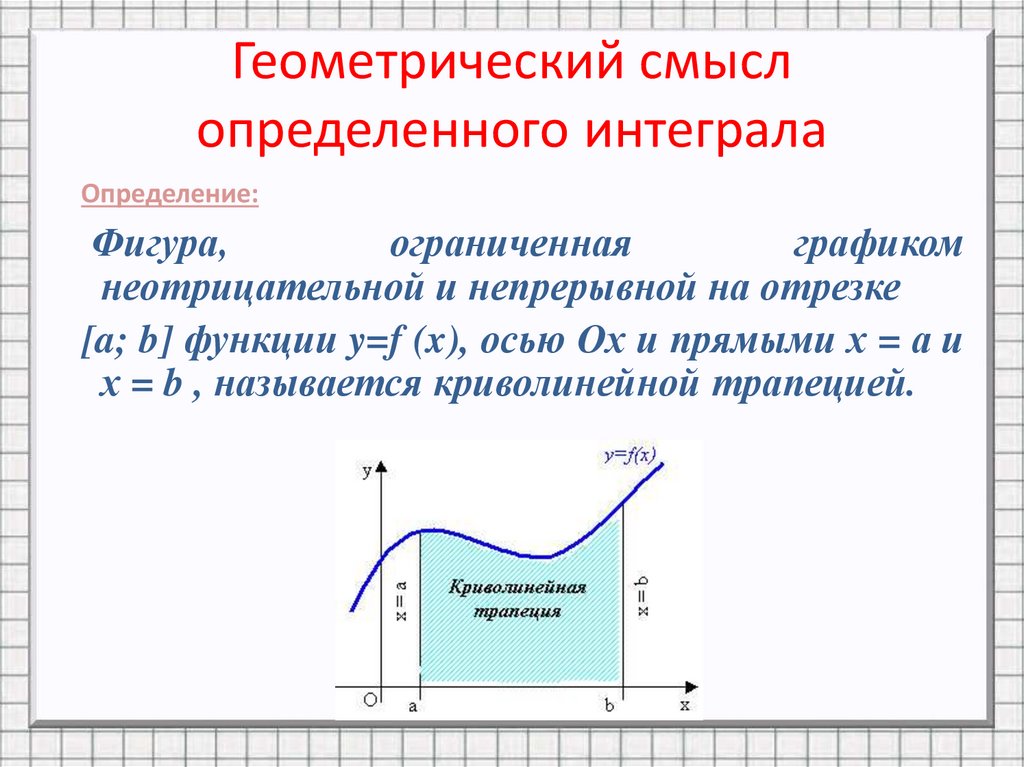
2. Геометрический смысл определенного интеграла
Определение:Фигура,
ограниченная
графиком
неотрицательной и непрерывной на отрезке
[a; b] функции y=f (x), осью Ох и прямыми х = а и
х = b , называется криволинейной трапецией.
3. Геометрический смысл определенного интеграла
Теорема:Определенный интеграл от a до b функции f(x) равен
площади S соответствующей криволинейной трапеции ,
b
т.е.
f x dx S
aBCb
a
Y
y=f(x)
C
B
S
а
b
X
4.
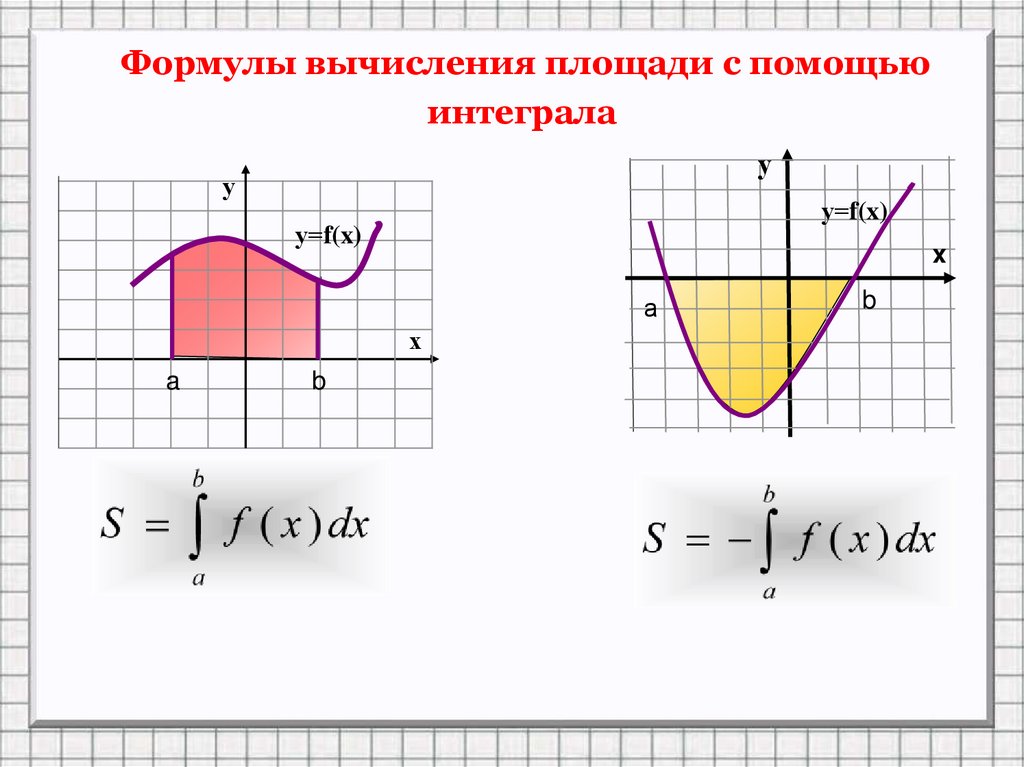
Формулы вычисления площади с помощьюинтеграла
у
у
у=f(x)
у=f(x)
x
а
х
a
b
b
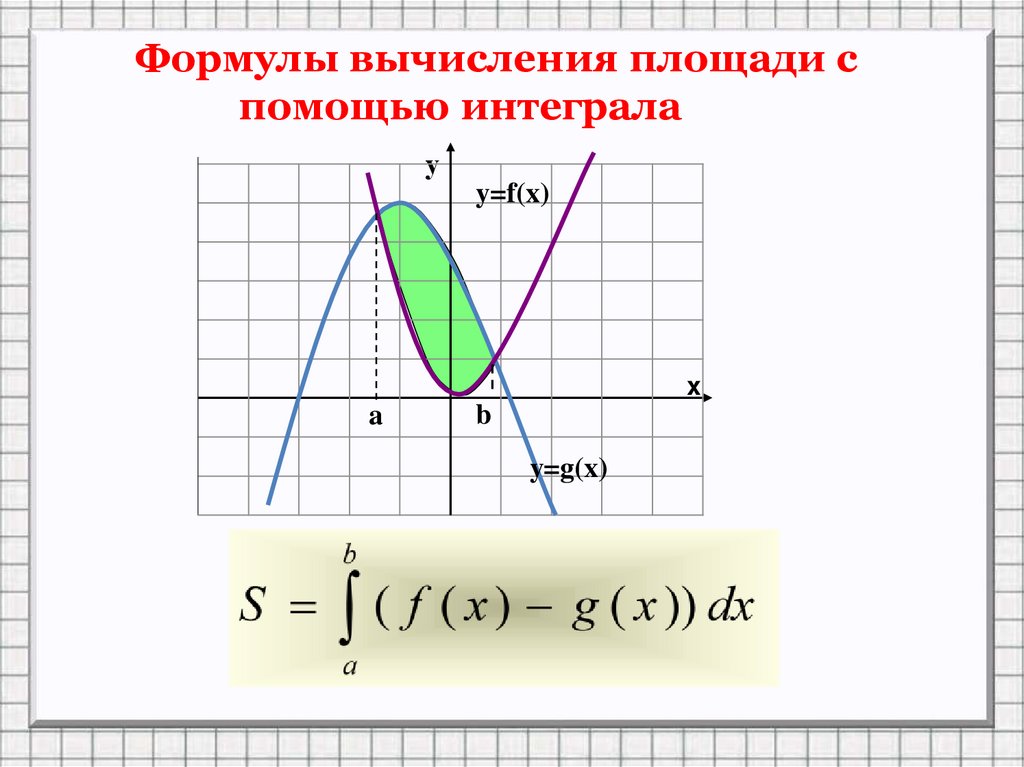
5.
Формулы вычисления площади спомощью интеграла
у
y=f(x)
x
a
b
y=g(x)
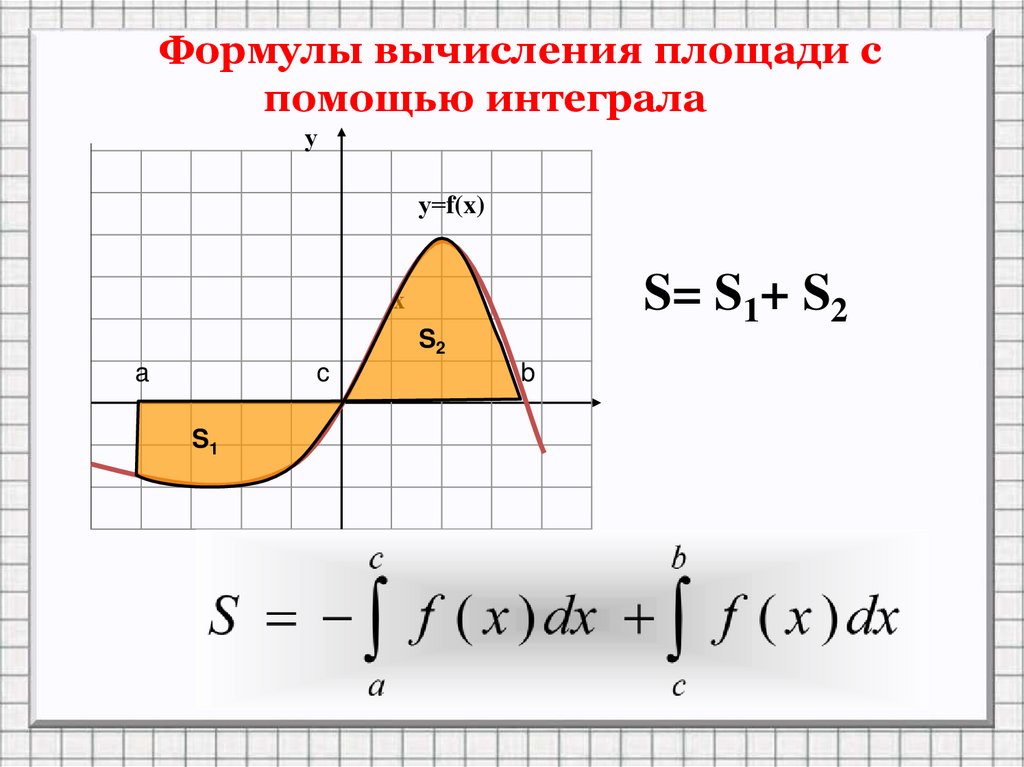
6.
Формулы вычисления площади спомощью интеграла
у
у=f(x)
S= S1+ S2
х
S2
a
c
S1
b
7. Построение графика линейной функции
Линейная функция:Определение: Линейной функцией называется функция вида у = кх +в
Графиком линейной функции является прямая.
Для построения прямой необходимо две точки:
х
У
у=х
5
4
3
2
1
x
5 4 3 2 11 0 1 2 3 4 5
2
3
4
5
x
7
8. Построение графика квадратичной функции
Квадратичная функцияОпределение: Квадратичной функцией называется функция вида
у = ax² + bx + c
Графиком линейной функции является парабола
Для построения необходимо определить:
1) направление ветвей :
если а>0, то ветви вверх
если а<0, то ветви вниз
в
2) вершина (х0, у0) : х0 = ,
у0 = у(х0)
2а
2
у=х
x x
5
4
3
2
1
5
4
3
2
11 0 1
2
3
4
5
x
2
3
4
5
8
9.
ПРАКТИКА:«Применение интегралов к
вычислению площадей»
10. Пример: Найдите площадь фигуры, ограниченной линиями
;Пример: Найдите площадь фигуры,
ограниченной линиями
у = -х2+2х+9,
x x 2x 9
3
у = 3х2-6х+5,
10
8
6
4
2
10 8
6
3
4
22 0 2
4
6
8
10
4
6
8 10
2
2 2
S (-х 2х 9)dx (3х 6 х 4)dx 34 24 10 ед
x
3
3
1
1
2
2
10
11. Задание 1: Найдите площадь фигуры, ограниченной линиями
;Задание 1: Найдите площадь фигуры,
ограниченной линиями
у=х2-8х+16,
у=6-х
11
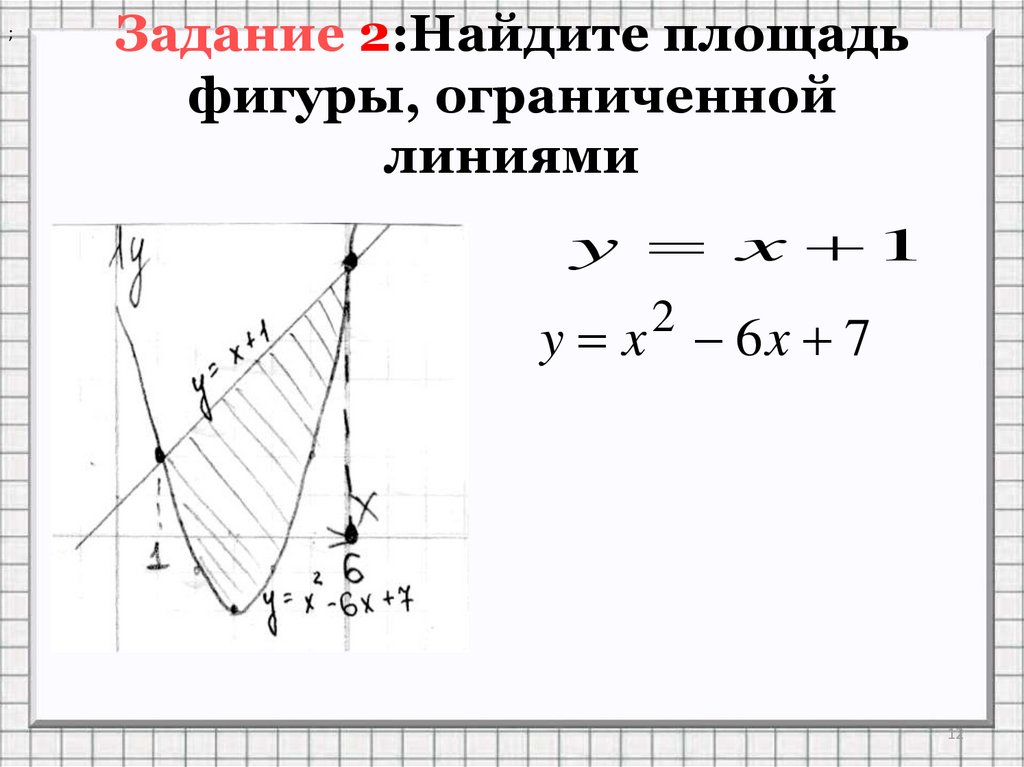
12. Задание 2:Найдите площадь фигуры, ограниченной линиями
;Задание 2:Найдите площадь
фигуры, ограниченной
линиями
y x 1
2
y x 6x 7
12







 Математика
Математика








