Похожие презентации:
Приложения определенного интеграла. Вычисление площади плоских фигур
1.
2. Вычисление площади плоских фигур
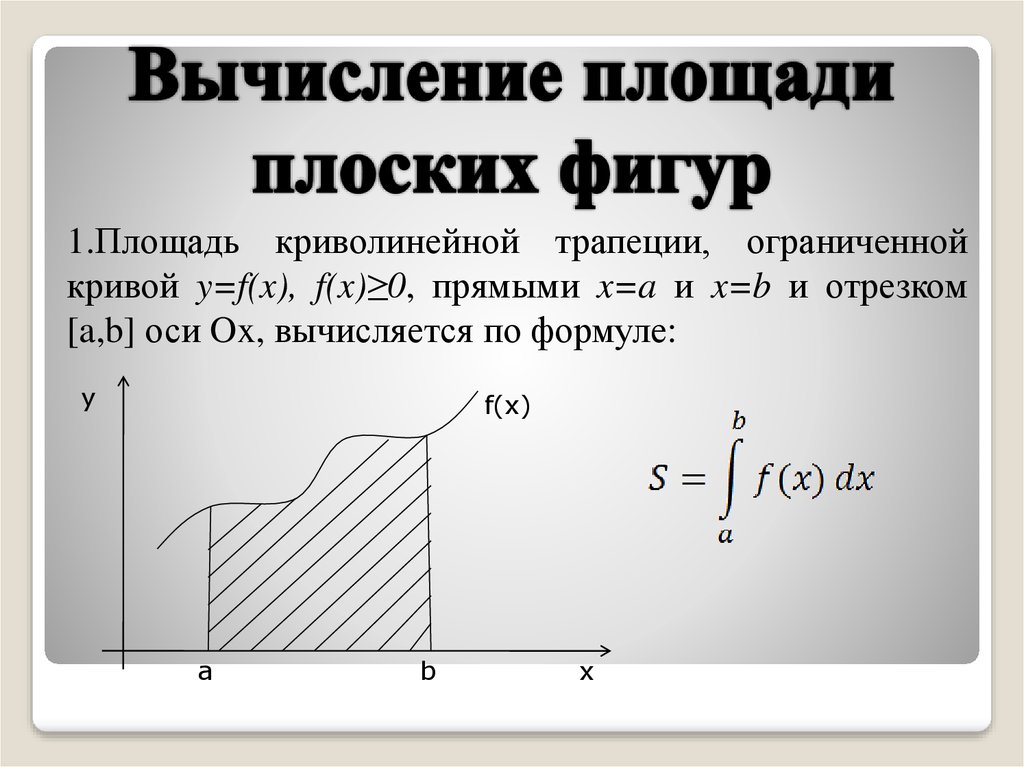
1.Площадь криволинейной трапеции, ограниченнойкривой y=f(x), f(x)≥0, прямыми x=a и x=b и отрезком
[a,b] оси Ox, вычисляется по формуле:
y
f(x)
a
b
x
3.
ya
x
f(x)
4.
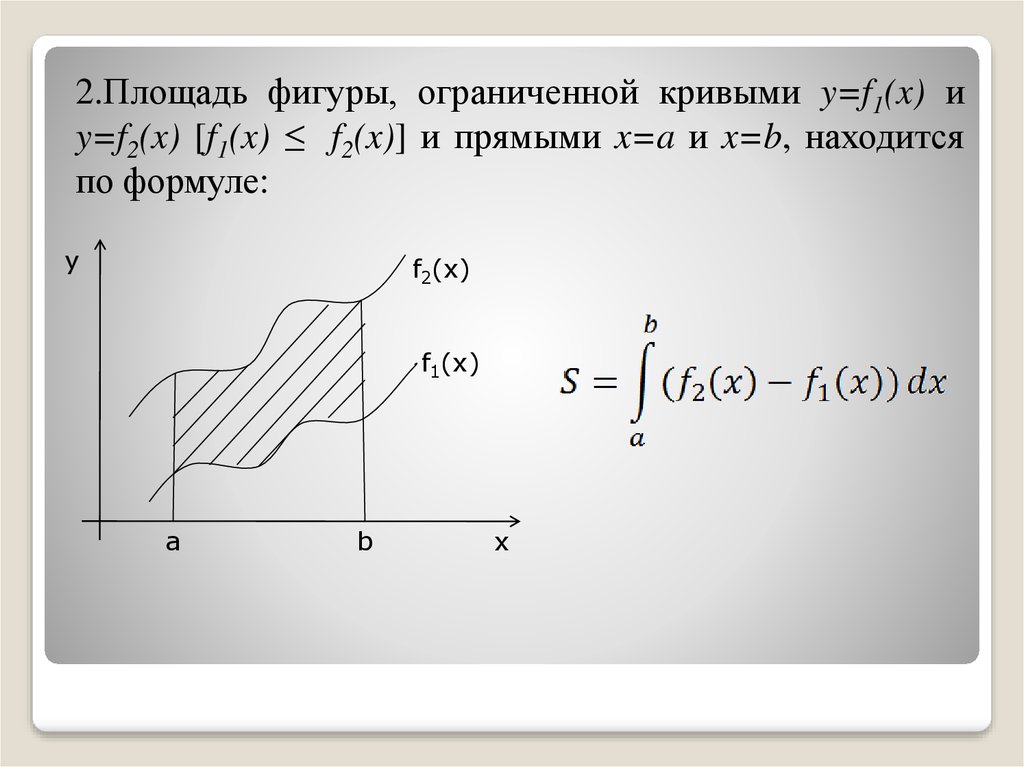
2.Площадь фигуры, ограниченной кривыми y=f1(x) иy=f2(x) [f1(x) ≤ f2(x)] и прямыми x=a и x=b, находится
по формуле:
y
f2(x)
f1(x)
a
b
x
5.
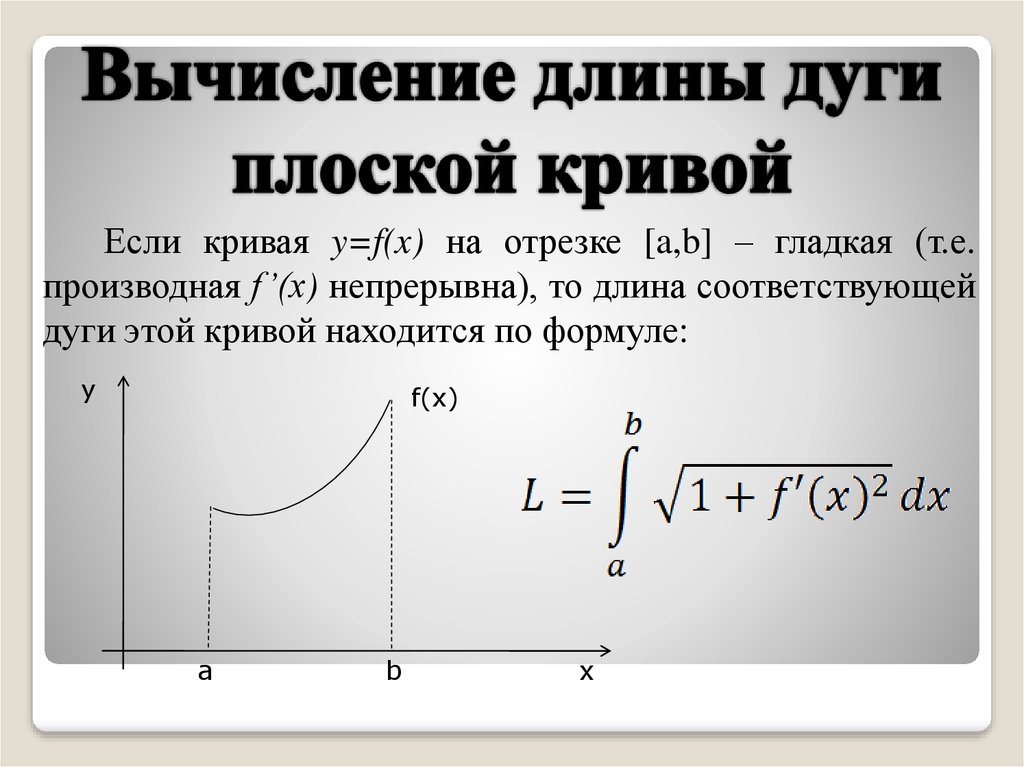
Если кривая y=f(x) на отрезке [a,b] – гладкая (т.е.производная f’(x) непрерывна), то длина соответствующей
дуги этой кривой находится по формуле:
y
f(x)
a
b
x
6.
Если криволинейная трапеция, ограниченная кривойy=f(x) и прямыми y=0, x=a, x=b, вращается вокруг оси
Ox, то объем тела вращения вычисляется по формуле:
f(x)
y
a
b
x
7.
Если криволинейная трапеция, ограниченнаякривой x=φ(y) и прямыми x=0, y=c, y=d, вращается
вокруг оси Oy, то объем тела вращения
вычисляется по формуле:
y
d
φ(x)
c
0
x
8.
Если фигура, ограниченная кривыми y1=f1(x) иy2=f2(x) [0≤f1(x)≤f2(x)] и прямыми x=a, x=b, вращается
вокруг оси Ox, то объем тела вращения находится по
формуле:
9.
Задача 1:Найти площади фигуры, ограниченной линиями:y=x2 и y=2x-x2
10.
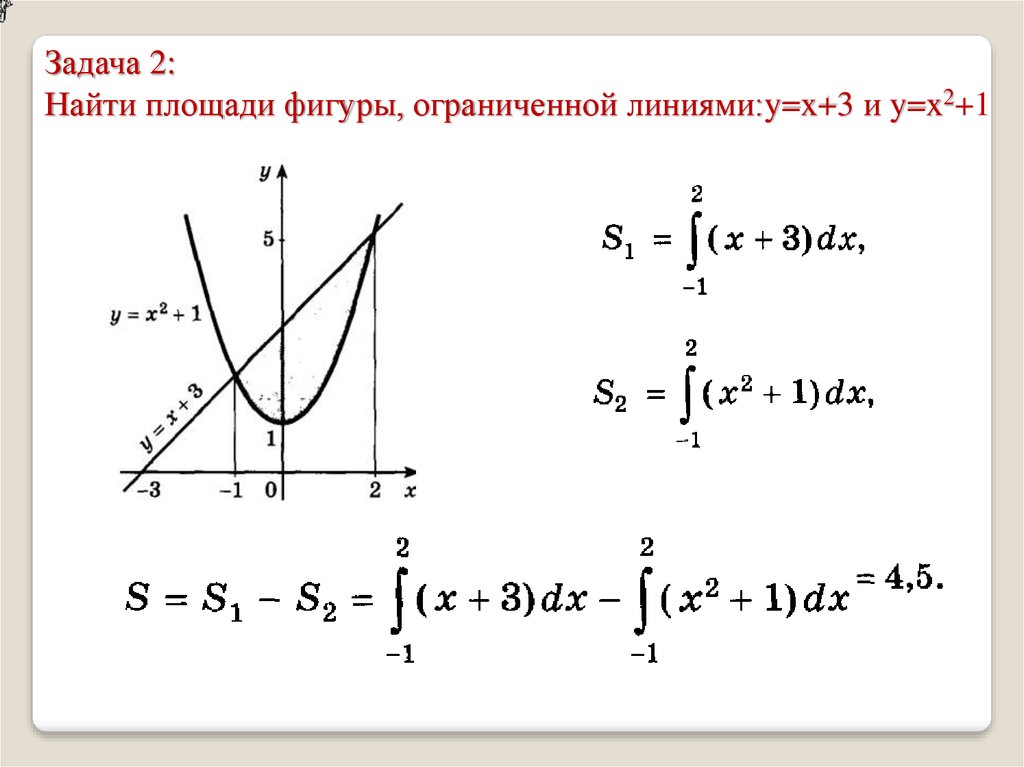
Задача 2:Найти площади фигуры, ограниченной линиями:y=x+3 и y=x2+1







 Математика
Математика








