Похожие презентации:
Уравнение касательной. Графиком какой функции является прямая?
1.
Уравнениекасательной
2. Ответьте на вопросы:
Графиком какой функции являетсяпрямая?
* Уравнение прямой?
* Как называется коэффициент при «х»?
* Чему равен угловой коэффициент
прямой?
* Что такое касательная?
* В каких точках кривой можно провести
касательну?
* Каким может быть взаимное
расположение касательной с осью абсцисс?
*
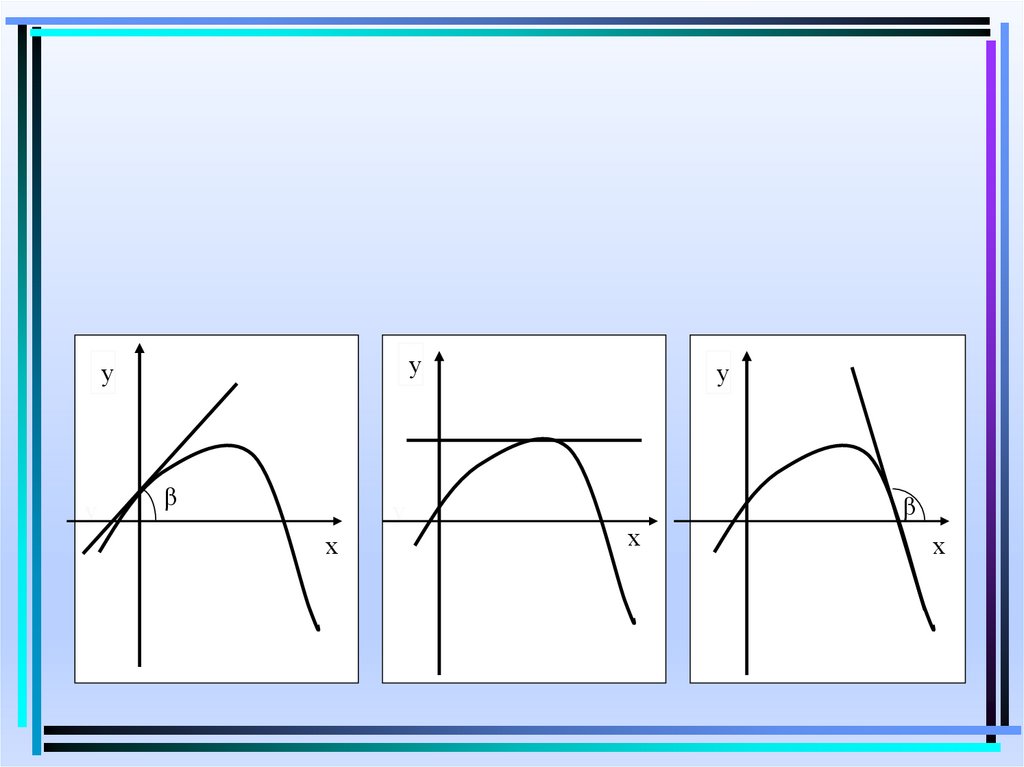
3.
уу
у
β
у
х
у
β
х
х
4. Итак:
Уравнение касательной имеетвид:
y = f(xo) + f `(xo)( x – xo)
5. Алгоритм
• Найти значение функции в точкехо, т.е f(xo)
• Вычислить производную
функции f `(x)
• Найти значение производной
функции в точке хо, т.е. f `(xo)
• Подставить полученные числа в
формулу y = f(xo) + f `(xo)( x – xo)
• Привести уравнение к
стандартному виду
6. Напишите уравнение касательной к графику функции f(х) = 2х - х² в точке с абсциссой х0= -1
y = f(x0) + f `(x0)( x – x0)1. f(x0) =.
f(– 1 ) = – 3;
2. f `(x) =
(2х - х² ) ’ = 2– 2x;
3. f `(x0) =
f `( – 1 ) = 4;
4. ( x – x0) = x + 1;
5. y = – 3 + 4( x + 1 );
y = 4x + 1 – уравнение касательной.
7.
y = f(x0) + f `(x0)( x – x0)8.
y = f (x0) + f `(x0)( x – x0)9.
Спасибо за урок!Всего доброго!
☺
☺








 Математика
Математика








