Похожие презентации:
Волны. Волновая поверхность
1. В о л н ы
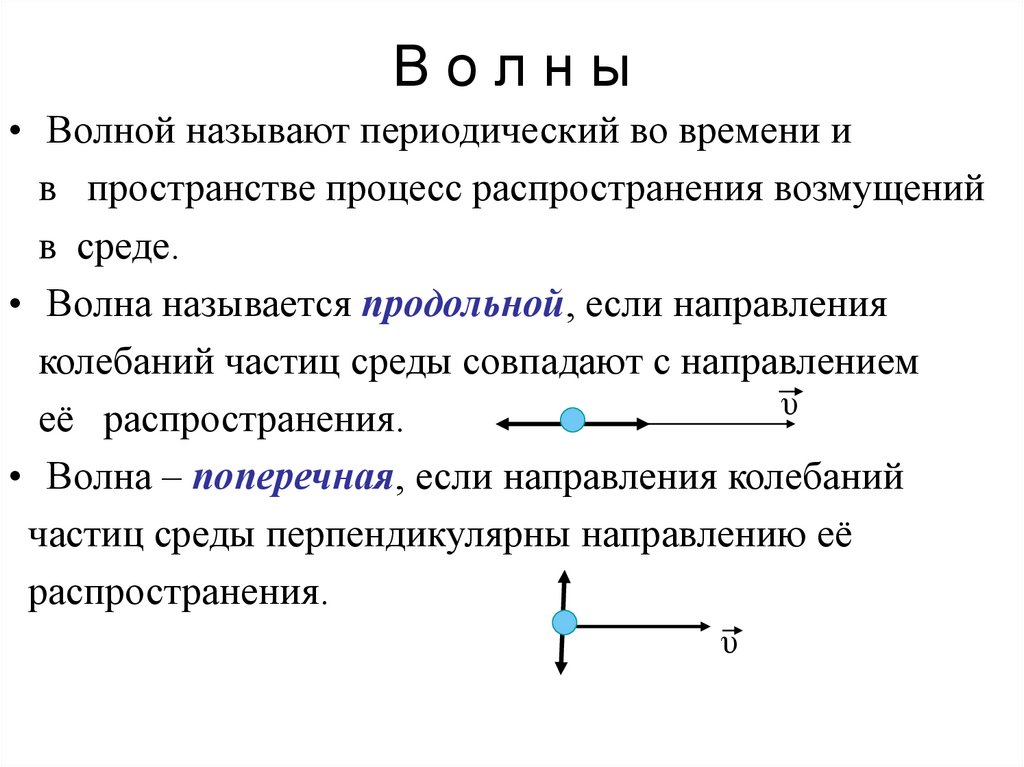
Волны• Волной называют периодический во времени и
в пространстве процесс распространения возмущений
в среде.
• Волна называется продольной, если направления
колебаний частиц среды совпадают с направлением
υ
её распространения.
• Волна – поперечная, если направления колебаний
частиц среды перпендикулярны направлению её
распространения.
υ
2.
• Волновая поверхность – геометрическое местоточек, колеблющихся в одинаковых фазах.
Фронт волны – граничная волновая поверхность,
до которой волна дошла в данный момент времени.
• Длина волны - расстояние между двумя
ближайшими волновыми поверхностями с
одинаковыми фазами (λ).
• Период – время одного полного колебания (Т)
• υ – фазовая скорость. Это расстояние, на которое
перемещается какая-либо фаза за единицу времени.
λ = υТ
3.
•ν – линейная частота колебаний, число колебанийв единицу времени.
•Связь циклической ω и линейной частоты ν с периодом:
ω = 2πν = 2π ⁄ Т
•k - волновое число, число длин волн, укладывающихся на
расстоянии 2π м:
k
k
2
2
T
2
k
k
4.
• Если в среде распространяется сложная волна,состоящая из колебаний нескольких частот, и
скорость волн зависит от их частоты ( имеет
место дисперсия), то форма волны непрерывно
меняется и для характеристики быстроты её
распространения используется групповая
скорость (u) – это скорость переноса энергии
волны.
u = υ – λ(dυ/dλ)
5. Уравнение волны
• Для описания колебаний точек среды в любой моментвремени при распространении волны вводится волновая
функция Ψ(r,t) – функция координат и времени.
Выражение, определяющее эту функцию, и есть
уравнение волны.
В точ. х = 0 Ψ(0,t) = Ψ0 (0)cosωt
А(х)
х
В т. А:
где τ = х/υ.
Для плоской волны:
Ψ(х,t) = Ψ0 (х)cosω(t –τ) ,
Ψ0 (0,t) = Ψ0 (х,t) = Ψ0
Ψ(х,t) = Ψ0 cos(ωt – ωх/υ) ,
Ψ(х,t) = Ψ0 cos(ωt – кх)
6. ВОЛНОВОЕ УРАВНЕНИЕ
Дифференциальное уравнение, решением которого являетсяуравнение волны, называется волновым уравнением. Для
гармонической волны, распространяющейся вдоль оси х, волновое
уравнение имеет вид:
2
d
d
2
=υ
,
2
2
dx
dt
2
где υ = ω/k.
r
Если волна распространяется вдоль некоторого
направления
r xi yj zk
то волновое уравнение примет вид:
d = υ2ΔΨ
dt 2,
2
2
2
2
где 2 2 2
x y z
- оператор Лапласа.
7.
Энергия волныdW = dWk + dWп
• dWk = υ2 dm /2 = υ2ρdV/2, ρ – плотность среды,
dV – элемент объёма.
• Можно показать, что dWп , равная работе по упругой
деформации среды, равна dWk, таким образом:
dW = 2dWk = υ2ρdV
Ψ(х,t) = Ψ0 cos(ωt – кх), υ= - Ψ0 ωsin(ωt - kx)
• dW = Ψ0 2ω2 ρsin2(ωt - kx)dV
dW~sin 2(ωt-kx)
8.
• Объёмная плотность энергии – энергия единицыобъёма:
w=dW/dV
• Поток энергии через поверхность S – энергия,
переносимая через эту поверхность в единицу
времени:
Фw = dW/dt = w u S ,
Фw = w u S
• Плотность потока энергии (вектор Умова) –
энергия, переносимая в единицу времени через
единицу площади:
j = wu
• Интенсивность волны:
J = <| j |> = < w>u
J ~ Ψ0 2
9.
Некоторые свойства электромагнитных волн□Электромагнитные волны – Е
процесс распространения в
среде электромагнитных
В
колебаний.
х
υ
Электромагнитная волна
поперечная: Е и Н .
Е, Н и υ образуют правовинтовую тройку векторов
Уравнение плоской гармонической электромагнитной
волны:
Е = Е0cos(ωt-kr )
Н = Н0cos(ωt-kr )
10.
• Скорость электромагнитной волны:1
0 0
с
• Плотность потока энергии (вектор Умова-Пойнтинга):
2
2
0 E 0 H
c
S w u w
2
S E, H
11.
Интерференция• В некоторую точку пространства приходят лучи от
двух когерентных источников:
Ψ1 = Ψ01соs(ωt kr1) = Ψ01соsφ1
Ψ2 = Ψ02соs(ωt kr2) = Ψ02соsφ2
М
S1
Ψ = Ψ1+ Ψ2= Ψ0соsφ
☼
Ψ02= Ψ012 + Ψ022 +2 Ψ01 Ψ02соsΔφ S☼
2
Δφ = |φ2 - φ1| = k | r2 - r1| = 2π Δr / λ
Δφ разность фаз, Δr – разность хода лучей.
r
2
|Ψ01- Ψ02| ≤ Ψ0 ≤ (Ψ01+ Ψ02)
Э
12.
•Если:или
Δφ = 0, 2π, 4π,…, (2mπ)
m = 0, 1, 2, 3,…
Δr = 0, λ, 2λ, 3λ, …, (m λ)
Ψ02= (Ψ012 + Ψ022 + 2 Ψ01 Ψ02 ) > (Ψ012 + Ψ022)
J = (J1+J2+2√J1J2 ) > (J1+J2)
или
Δφ = 2mπ
– условие максимума
Δr = m λ
•Если:
Δφ = π, 3π, 5π,…, (2m+1) π
или
Δr = λ/2, 3λ/2, …, (2m+1) λ/2
Ψ02= (Ψ012 + Ψ022 - 2 Ψ01 Ψ02 ) < (Ψ012 + Ψ022)
J = (J1+J2 - 2√J1J2 ) < (J1+J2)
или
Δφ = (2m+1)π
Δr = (2m +1)λ/2
– условие минимума











 Физика
Физика








