Похожие презентации:
Физика волновых процессов
1.
МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РФФедеральное государственное автономное образовательное учреждение высшего образования
КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ИНСТИТУТ ФИЗИКИ
ОТДЕЛЕНИЕ РАДИОФИЗИКИ
И ИНФОРМАЦИОННЫХ СИСТЕМ
И. А. Насыров
Конспекты лекций по курсу
ФИЗИКА ВОЛНОВЫХ ПРОЦЕССОВ
Электронное учебное пособие
Казань
2017
2.
УДК 530.19; 530.182Рекомендовано к изданию
Учебно–методической комиссией
Института физики
Казанского (Приволжского) федерального университета
(протокол №8 от 30 июня 2017 г.)
Рецензент:
доцент кафедры компьютерных систем КНИТУ–КАИ им. А. Н. Туполева,
к.ф.-м.н. Е. С. Белашова
Насыров И. А.
Конспекты лекций по курсу «Физика волновых процессов». Электронное учебное пособие — Казань: Институт физики КФУ, 2017. — 163 с.
Учебное пособие предназначено для студентов, обучающихся по направлению 03.03.03 — Радиофизика и подготовлено в поддержку курса «Физика
волновых процессов», который читается студентам бакалавриата третьего года обучения. Кроме этого, пособие будет полезно магистрантам и аспирантам
радиофизического профиля Университета для самостоятельного рассмотрения вопросов, связанных с изучением волновых процессов в линейном приближении.
Для эффективной работы с учебным пособием необходимо использовать
Adobe Acrobat Reader X (или более поздние версии), которому разрешить
использование интерактивного содержимого PDF–документа. Для доступа к
видеофрагментам, расположенным на YouTube, необходимо подключение к
сети INTERNET.
© И. А. Насыров, 2017.
© Институт физики КФУ, 2017.
3.
3Содержание
1 Волновое уравнение
1.1 Некоторые сведения из теории колебаний . . . . . . . . . . . . .
1.2 Волновой процесс . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1 Понятие волнового движения . . . . . . . . . . . . . . . .
1.2.2 Виды волн . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Волновое уравнение . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.1 Вывод уравнения поперечных волн на струне . . . . . . .
1.3.2 Решение волнового уравнения . . . . . . . . . . . . . . . .
1.3.3 Энергия поперечных колебаний струны . . . . . . . . . .
6
6
10
10
16
20
20
23
25
2 Основные понятия
28
2.1 Фазовая скорость . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.2 Импеданс . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.3 Отражение и прохождение волн . . . . . . . . . . . . . . . . . . 32
2.3.1 Два случая отношения импедансов граничащих сред . . 35
2.3.2 Согласование импедансов двух сред . . . . . . . . . . . . 37
2.4 Стоячие волны . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.4.1 Коэффициент стоячей волны . . . . . . . . . . . . . . . . 41
2.5 Дисперсия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2.5.1 Закон дисперсии для реальной струны пианино . . . . . 43
2.6 Групповая скорость . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.6.1 Бездисперссионная мода . . . . . . . . . . . . . . . . . . . 46
2.6.2 Дисперсионная мода . . . . . . . . . . . . . . . . . . . . . 48
3 Электромагнитные волны диапазона радиочастот
58
3.1 Волновое уравнение для электромагнитных волн . . . . . . . . . 60
3.1.1 Уравнения Максвелла . . . . . . . . . . . . . . . . . . . . 60
3.1.2 Вывод волнового уравнения для среды без потерь . . . . 65
3.1.3 Электромагнитные волны в средах с потерями . . . . . . 71
3.2 Критерий разделения сред на диэлектрики и проводники . . . . 76
3.3 Среда — полупроводник . . . . . . . . . . . . . . . . . . . . . . . 78
3.3.1 Частные случаи: среда — диэлектрик . . . . . . . . . . . 83
4.
43.3.2 Частные случаи: среда — проводник . . . . . . . . . . . . 85
3.4 Принцип Гюйгенса и зоны Френеля . . . . . . . . . . . . . . . . 89
4 Отражение и преломление электромагнитных волн
на плоской границе раздела двух сред
94
4.1 Основные соотношения . . . . . . . . . . . . . . . . . . . . . . . 94
4.1.1 Граничные условия . . . . . . . . . . . . . . . . . . . . . . 95
4.1.2 Принятые обозначения . . . . . . . . . . . . . . . . . . . . 96
4.1.3 Отражение и преломление плоских волн . . . . . . . . . . 97
4.2 Отражение при горизонтальной поляризации падающей волны . 99
4.3 Отражение при вертикальной поляризации падающей волны . . 101
4.4 Коэффициенты отражения для различных сред . . . . . . . . . 102
4.4.1 Среда 2 — диэлектрик . . . . . . . . . . . . . . . . . . . . 102
4.4.2 Среда 2 — полупроводник . . . . . . . . . . . . . . . . . . 105
4.4.3 Среда 2 — проводник . . . . . . . . . . . . . . . . . . . . 106
4.5 Влияние шероховатости отражающей поверхности . . . . . . . . 107
4.5.1 Критерий Релея . . . . . . . . . . . . . . . . . . . . . . . 107
4.5.2 Закон Ламберта . . . . . . . . . . . . . . . . . . . . . . . . 108
4.6 Отражение при произвольной поляризации падающей волны . . 110
5 Электромагнитные волны в волноводе
112
5.1 Общий вид решения волновых уравнений в волноводе . . . . . . 112
5.2 Дисперсия в волноводах . . . . . . . . . . . . . . . . . . . . . . . 114
5.2.1 Режим отсечки . . . . . . . . . . . . . . . . . . . . . . . . 116
5.3 Типы волн в волноводах . . . . . . . . . . . . . . . . . . . . . . . 117
5.3.1 Условия существования бездисперсионных волн в волноводе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
5.4 Прямоугольный волновод . . . . . . . . . . . . . . . . . . . . . . 119
5.4.1 T E–волны (Ez = 0) . . . . . . . . . . . . . . . . . . . . . 120
5.4.2 T M –волны (Hz = 0) . . . . . . . . . . . . . . . . . . . . . 123
5.5 Одномодовый диапазон . . . . . . . . . . . . . . . . . . . . . . . 124
5.5.1 Основная мода . . . . . . . . . . . . . . . . . . . . . . . . 124
5.5.2 Коаксиальный волновод . . . . . . . . . . . . . . . . . . . 128
5.
56 Радиоволны в неоднородных средах
132
6.1 Геометрооптическое приближение . . . . . . . . . . . . . . . . . 133
6.1.1 Уравнение луча . . . . . . . . . . . . . . . . . . . . . . . . 134
6.1.2 Геометрическая оптика слоисто–неоднородной среды . . 137
6.2 Рефракция лучей в плоско–слоистой среде . . . . . . . . . . . . 141
6.2.1 Случай монотонного увеличения показателя преломления с высотой . . . . . . . . . . . . . . . . . . . . . . . . . 141
6.2.2 Случай монотонного уменьшения показателя преломления с высотой . . . . . . . . . . . . . . . . . . . . . . . . . 142
6.3 Условия применимости геометрической оптики . . . . . . . . . . 143
6.3.1 Критерии применимости геометрической оптики . . . . . 144
6.4 Рефракция лучей в сферически–слоистой среде . . . . . . . . . 145
6.4.1 Электрические параметры ионосферы . . . . . . . . . . . 145
6.4.2 Расчет траекторий лучей . . . . . . . . . . . . . . . . . . 149
6.5 Дифракция радиоволн . . . . . . . . . . . . . . . . . . . . . . . . 158
6.5.1 Эффект «усиления препятствием» . . . . . . . . . . . . . 161
Список рекомендованной литературы
163
6.
6ТЕМА 1
Волновое уравнение
1.1
Некоторые сведения из теории колебаний
Под колебанием понимаем некоторый процесс повторяющегося движения около положения равновесия. То есть процесс, которой можно описать
некоторой периодической функцией U = f (t), такой, что при любом t и определенном T
f (t + T ) = f (t),
где T называется периодом функции.
Нетрудно показать, что если функция имеет период, то она имеет бесчисленное множество периодов. Действительно,
f (t + T + T ) = f (t + T ) = f (t).
Следовательно, 2T — тоже период, и вообще любое целое кратное от периода
есть период. Принято, говоря без каких-либо дальнейших указаний о периоде,
иметь в виду наименьший период.
Построить периодическую функцию можно весьма разнообразными способами. Можно, например, задать в некотором интервале (0, T ) любую функцию и затем повторять ее неограниченное число раз слева и справа. Следова-
Рисунок 1.1 — Произвольная периодическая функция
тельно, построенные таким путем функции в общем случае не будут непрерывны, а будут иметь скачки на границах интервала (0, T ).
Таким образом, в рассмотрение теории колебаний входят не только непрерывные, но и разрывные функции.
7.
7Функции, принадлежащие к классу периодических, весьма разнообразны. Среди них есть функции, образующие подкласс, играющий особую роль,
а именно синусообразные (гармонические) функции.
Рассмотрим опыты с маятником. Таким образом, в общем случае пове-
(Маятник и его осциллограмма)
Рисунок 1.2 — Маятник и его осциллограмма
дение маятника будет описываться синусообразной функцией вида:
U = f (t) = U0 cos
2π
T
!
t−ϕ .
(1.1)
Здесь U0 — максимальное откронение маятника от положения равновесия
(ампитуда колебаний); T — период колебаний маятника; ϕ — начальная фаза
(положение, из которого маятник был запущен).
Более употребимой является величина, обратная периоду колебания —
рад
2π
ω = , называемая циклической частотой, которая измеряется в
.
T
сек
8.
8Таким образом, синусообразную функцию (1.1) можно записать в виде:
U = U0 cos (ωt − ϕ) .
(1.2)
С точки зрения технических приложений более удобной является величи1
на f = , называемая линейной частотой, или просто частотой. Измеряется
T
!
1
в Герцах и обозначается Гц 1 Гц =
.
сек
Необходимо сказать однако, что вид осциллограммы, описываемой уравнением (1.2), будет сильно зависеть от начальных условий, как это видно из
анимации, представленной на рисунке 1.3.
(Зависимости от начальных условий)
Рисунок 1.3 — Зависимость характера колебаний от начальных условий
Теория колебаний и волн изучает общий характер движения, взятого
в целом, и здесь используются два основных подхода — кинематический и
динамический.
9.
9Суть кинематического подхода к описанию движения физической системы заключается в следующем: можно, например, нанести на одну диаграмму осциллограммы всех возможных функций вида (1.2), как это показано
на рисунке 1.4. По получившейся диаграмме находить общие зависимости в
движениях колебательной системы.
Рисунок 1.4 — Набор осциллограмм, получившихся при различных начальных условиях запуска маятника
Однако необходимо заметить, что в подавляющем большинстве случаев
такой подход к описанию колебательных систем является малопродуктивным. Большое количество осциллограмм, описывающих частные движения
колебательной системы, нанесённые на одну диаграмму, затрудняют проведение качественного анализа системы в целом. Кроме этого, как видно из
рисунка 1.4, на диаграмму можно нанести только ограниченный во времени
период работы колебательной системы. Таким образом, рассмотреть поведение этой системы за временны́ми пределами ограниченными осью абсцисс
диаграммы не представляется возможным.
Более продуктивным методом найти решение основных вопросов, которыми занимается Теория колебаний и волн, является динамический подход.
Суть динамического подхода сводится к следующему: строится дифференциальное уравнение, которому подчиняются все движения физической системы, независимо от начальных условий. Затем с помощью математических
10.
10рассуждений из дифференциального уравнения выводятся уравнения частных движений, удовлетворяющие тем или иным начальным условиям.
Для примера приведём уравнение гармонического осциллятора:
d2 x
dx
+
2γ
·
+ ω02 x = p(t),
2
dt
dt
(1.3)
где γ — параметр, описывающий потери в системе; ω0 — собственная частота
гармонического осцилятора; p(t) — некоторое периодическое внешнее воздействие на систему.
Для системы, не имеющей потерь (γ = 0) и совершающей свободные
колебания (p(t) = 0), это уравнение запишется в виде
d2 x
dt2
+ ω02 x = 0.
(1.4)
Далее, формулируя начальные условия, получаются решения, описывающие
частные движения колебательной системы.
Таким образом, колебательный процесс — это ограниченные в пространстве (и часто повторяющиеся) движения в окрестности некоторого среднего
положения. Колебательный процесс можно описать конечным набором параметров, изменяющихся во времени. Например, для математического маятника — это угол отклонения нити от вертикали; для связанных контуров —
напряжения и токи в первом и втором контурах.
Волна — это распространение колебаний в пространстве, происходящее
с конечной скоростью.
1.2
1.2.1
Волновой процесс
Понятие волнового движения
Колебательная система может отдавать энергию во внешнюю среду. Эта
передача энергии становится возможной благодаря тому, что вследствие упругости среды отдельные небольшие участки ее сами представляют собой миниатюрные колебательные системы.
Находясь в какой-либо среде, колебательная система взаимодействует с
непосредственно прилегающими к ней частицами. Совершая свои колебания,
она создает вокруг себя периодический ряд возмущений, т. е. действует на
11.
11прилегающие частицы как некоторая периодическая внешняя сила. Эта сила
заставляет частицы среды совершать колебания с частотой вынуждающей
силы, причем колебательный процесс благодаря взаимодействию частиц будет распространяться в среде с некоторой определенной, характерной для
свойств этой среды скоростью.
Очевидно, что частица среды, находящаяся на расстоянии x от места
начального возмущения (x = 0), начнет колебаться только тогда, когда до
нее дойдет распространяющийся в среде колебательный процесс.
Обозначим скорость распространения колебательного процесса через v.
Колебательный процесс дойдет до рассматриваемой частицы через промежуток времени
x
τ= .
v
Если колебания системы в начале координат можно выразить как
U (t, 0) = U0 sin(ωt),
то колебания рассматриваемой частицы с координатой x будут происходить
по такому же синусоидальному закону, но с запозданием на отрезок времени
τ ; таким образом, мы можем написать для частицы уравнение
h
x i
U (t, x) = U0 sin [ω (t − τ )] = U0 sin ω t −
.
v
(1.5)
Это уравнение определяет смещение частицы с координатой x в функции
от времени и от расстояния до начала координат. Если, однако, одновременно рассматривать точки, лежащие на одной прямой, проходящей через начальную точку, то, задавая для x различные значения, мы можем выяснить
посредством уравнения (1.5) распределение смещений вдоль выбранной нами
прямой. В этом случае мы рассматриваем выражение (1.5) как функцию от
одного только x, а изменение процесса во времени демонстрируется на нижней панели рисунка 1.5. Рисунок 1.5 поясняет, как начинается и происходит
передача колебательного движения в среде, когда частицы среды колеблются перпендикулярно к направлению передачи движения. Мы видим, что этот
процесс периодичен не только во времени, но и в пространстве. По сходству
явления с одним из его частных случаев (именно с волнами на поверхности воды) этот процесс называют волновым, а распространяющееся в среде
12.
12периодическое (или хотя бы мгновенное) возмущение — волной. Уравнение
(1.5) есть уравнение волн, распространяющихся в положительном направлении оси X.
(Понятие волнового движения)
Рисунок 1.5 — Распространение возмущения по системе связанных осцилляторов (верхняя панель) и осциллограмма движения осциллятора №1, отмеченного зеленым маркером на верхней панели (нижняя панель)
Чтобы с большей ясностью показать, что уравнение (1.5) выражает процесс, периодичный и во времени и в пространстве («волны»), мы можем поступить следующим образом.
Рассматривая сначала течение процесса в некоторой определенной точке
среды (x = const), мы можем представить себе начало координат именно в
этой точке; тогда x = 0 и уравнение (1.5) принимает вид
U (t) = U0 sin(ωt).
Это уравнение есть уравнение колебаний выбранной частицы с координатой x = const; оно определяет периодичность волнового процесса во времени
(нижняя панель на рисунке 1.5).
Интересуясь распределением смещений в пространстве в некоторый определенный момент времени (t = const), мы можем выбрать именно этот мо-
13.
13мент за начальный, т. е. положить t = 0; тогда
x
2π
U (x) = U0 sin ω
= U0 sin
x .
v
vT
Введём величину λ, определяемую равенством:
λ = vT,
(1.6)
перепишем уравнение (1.5) в следующем виде:
2π
U (x) = U0 sin
x .
λ
Последнее уравнение выражает пространственную периодичность процесса.
Введенная в него величина λ имеет простой физический смысл. Так как T
есть период колебаний, а v — скорость их распространения, то произведение vT определяет, очевидно, расстояние, на которое распространяется колебательный процесс за время одного периода. Следовательно, две частицы,
отделенные друг от друга интервалом λ = vT , колеблются с одной и той
же фазой; каждая из них проходит через нулевое положение одновременно с
другой. Величину λ называют длиной волны.
Критерий разделения процессов на колебательные и волновые
Если характерные размеры системы L < vT (v — скорость распространения возмущения; T — время заметного изменения возмущения), о процессе
можно говорить как о колебательном.
В случае L > vT процесс можно считать волновым, а систему распределенной.
Если говорить о радиотехнике, то теория колебаний была развита раньше, чем волновые принципы. Исторически это было связано с использованием на начальном этапе освоения радиодиапазона длин волн, намного превосходящих размеры радиоэлектронных устройств, и для анализа их работы
можно было ограничиться колебательными представлениями. С переходом к
более коротким волнам размеры передающих и приемных устройств оказались соизмеримы и больше длины рабочей волны. Это потребовало перехода
14.
14к представлениям о радиосистемах с распределенными параметрами, работу
которых можно было анализировать, используя волновые принципы.
Частота и волновое число
Из теории колебаний известно, что величина, обратная периоду колебания, назвается циклической частотой:
ω=
2π
.
T
(1.7)
С другой стороны, длина волны λ, которая по своей сути является пространственным периодом, также имеет обратную величину — волновое число, которое играет роль «пространственной частоты».
k=
2π
.
λ
(1.8)
Таким образом, уравнение (1.5), описывающее распространение гармонической волны вдоль оси X, мы можем переписать в виде:
U (t, x) = U0 sin (ωt − kx) .
(1.9)
Фактически, волновое число определяется скоростью возрастания фазового угла, приходящейся на единицу длины, для фиксированного момента
времени и равно
ω
k= .
(1.10)
v
Выражение (1.5) записано для случая гармонической волны, бегущей вправо
(в направление возрастания положительных x). Если волна бежит влево, то
знак величины фазового угла надо изменить на обратный, т. к. колебания
в точке x начинаются раньше, чем в x = 0. Поэтому аргумент (ωt − kx)
соответствует волне, распространяющейся вправо, а (ωt + kx) — влево.
Общие для волн всех типов характеристики
Волновые процессы в настоящее время интенсивно изучаются в различных областях физики:
- электродинамике,
15.
15- физике плазмы,
- оптике,
- радиофизике,
- акустике,
- гидродинамике
и других областях науки.
Механизмы распространения возмущений в этих областях сильно различаются друг от друга. Однако имеются характеристики, общие для волн всех
типов. Важнейшими среди них являются
- энергия,
- импульс,
- скорость распространения возмущения.
Подобно движущемуся объекту, бегущие волны несут энергию и обладают
импульсом. Для распространения волны между двумя точками пространства
нужно определенное время. Это означает, что волны обладают конечной скоростью. Ясно, что ее величина в различных средах сильно отличается. По
приведенным выше характеристикам волны внешне схожи с каким-либо движущимся объектом. Однако необходимо иметь в виду, что отдельные частицы
среды не распространяются с волнами. Они колеблются относительно своих
положений равновесия в поперечном или продольном направлении. В качестве волн наблюдается не распространение частиц (отдельных осцилляторов)
в среде, а их фазовые соотношения.
Важно уяснить себе, что частицы среды не увлекаются движущейся
волной; они совершают лишь колебательные движения около положения равновесия. Щепка, брошенная на поверхность непроточной воды, лишь колеблется вверх и вниз, оставаясь в одном и том же месте поверхности. Скорость
волны не есть скорость движения материальных частиц, это есть скорость
распространения импульса, вызывающего смещение частиц.
При волновом движении существуют три скорости, представляющие различные физические величины.
1. Скорость частиц — это скорость гармонических колебаний осциллятора
около положения равновесия;
2. волновая (или фазовая) скорость — скорость распространения в среде
поверхностей с одинаковой фазой;
16.
163. групповая скорость — скорость распространения группы волн (или волнового пакета).
Перенос энергии в среде осуществляется с групповой скоростью. Для монохроматических волн фазовая и групповая скорости совпадают.
Для многих видов волн характерно свойство линейности. Волны называют линейными, если они не влияют на распространение других волн и
вследствие этого их совокупность представляет собой простую сумму этих
волн. Многие волны близки к линейным. В общем же случае волны бывают
нелинейными. В настоящее время нелинейные волновые процессы интенсивно исследуются в различных областях физики (изучение нелинейных процессов при распространении мощных звуковых волн, эффекты взаимодействия
световых волн, генерируемых оптическими квантовыми генераторами, эффекты взаимодействия мощного электромагнитного излучения с плазмой и
т.д.). Увеличение мощности используемых в физическом эксперименте и на
практике источников звуковых волн, световых и радиополей привело к тому, что нелинейные эффекты при распространении волн приобрели столь же
большое значение, как и нелинейные процессы в теории колебаний.
В настоящем лекционном курсе мы рассмотрим ряд особенностей электромагнитных волн радиодиапазона. Многие фундаментальные свойства электромагнитных волн изучаются в курсах «Оптика» и «Электродинамика». Мы
повторим ряд сведений из этих курсов. Однако основное внимание будет уделено вопросам распространения электромагнитных волн, которые не затрагиваются в этих курсах.
Ряд важных фундаментальных величин и понятий физики радиоволн,
являющихся общими для волн любой природы, вводится на примере простейших типов волн — поперечных волн на струне. Это сделано для упрощения
выводов и для облегчения понимания обсуждающихся вопросов. К ним относится вывод волнового уравнения, понятие импульса, фазовой и групповой
скорости, согласование сред с различными импедансами.
1.2.2
Виды волн
Продольные волны
В газах и жидкостях при попытке сблизить два соседних слоя или удалить их друг от друга возникают возвращающие силы, препятствующие де-
17.
17Рисунок 1.6 — Продольная волна
формации сжатия или растяжения. Колебания частиц происходят в направлении возвращающих сил, поэтому в таких средах возможны лишь волны, в
которых колебания частиц совпадают с направлением распространения волны (рисунок 1.6). Такие волны называют продольными.
Продольные волны представляют собой чередующийся ряд сгущений и
разрежений, причем длина волны λ — расстояние между двумя соседними
сгущениями или разрежениями.
Поперечные волны
Рисунок 1.7 — Поперечная волна
В твердом теле деформация сдвига вызывает волну, распространяющуюся в направлении, перпендикулярном к направлению смещения частиц. Волна, в которой колебательное движение совершается перпендикулярно к направлению распространения колебаний, называется поперечной.
18.
18Примеры поперечных волн:
- волны, бегущие вдоль натянутой струны;
- крутильные волны, вызываемые попеременным закручиванием и раскручиванием конца длинного стержня.
Продольные и поперечные колебания волно-несущей среды представляют собой частные случаи волнового процесса. Существуют и другие волны, в
которых колебательные движения складываются из одновременных продольных и поперечных смещений.
Волны вздутия
Рисунок 1.8 — Волны вздутия
Если ударить молотком по торцевому срезу круглого стержня, то вдоль
него бежит волна, смещения частиц будут продольными только вдоль оси
стержня, по мере приближения к поверхности частицы стержня будут совершать поперечные колебания возрастающей амплитуды (рисунок 1.8). Такие
волны назвают волнами вздутия.
Волны вздутия возникают в жидкостях (и газах), заключенных в трубы с податливыми стенками. Условием возникновения таких волн является
возможность смещения частиц перпендикулярно к поверхности.
19.
19Рисунок 1.9 — Поверхностные волны
Поверхностные волны
Законы распространения поверхностных волн более сложны, чем законы
распространения прочих видов волн.
Рисунок 1.10 — Частицы волнующейся жидкости движутся по круговым (эллиптическим) орбитам
Колебательные траектории частиц, участвующих в распространении поверхностной волны, не являются прямолинейными; частицы описывают замкнутые эллиптические орбиты, как это показано на рисунке 1.10.
Простые синусоидальные волны на поверхности могут существовать только при амплитудах, малых сравнительно с длиной волны; таковы, например,
волны морских приливов, длина которых может доходить до сотен километров.
20.
20Обычные же волны, например корабельные волны или волны от брошенного камня, имеют профиль, резко отличающийся от синусоиды: плоские
длинные впадины и острые короткие верхушки на рисунке 1.10). Поверхностная волна большой амплитуды увлекает с собой колеблющиеся частицы,
которые в этом случае описывают уже не круговые, а более сложные траектории. Именно поэтому большие волны выбрасывают на берег плавающие на
них предметы.
Волны возникают не только на свободной поверхности жидкости, но вообще на поверхности раздела двух жидкостей, например масла и воды или
соленой и пресной воды, а также на диффузионной границе двух газов различной плотности. Возникновением волн на поверхности раздела пресной и
соленой воды объясняется интереснейшее явление — так называемая «мертвая вода», наблюдаемая недалеко от устьев рек, особенно в скандинавских
фиордах. Идущие корабли вдруг тормозятся вследствие того, что корабль,
попав на поверхность раздела пресной и соленой воды, разводит на ней невидимую с поверхности моря волну.
1.3
Волновое уравнение
В теории волн фундаментальное значение имеет линейное волновое уравнение в частных производных второго порядка гиперболического типа:
∆U −
1 ∂ 2U
= 0,
v 2 ∂t2
(1.11)
где ∆ — оператор Лапласа
∂ 2U ∂ 2U ∂ 2U
∆U =
+
+
.
∂x2
∂y 2
∂z 2
Роль этого уравнения аналогична роли уравнения гармонического осциллятора (1.4) в теории колебаний. Уравнения типа (1.11) называют уравнениями
д’Аламбера.
1.3.1
Вывод уравнения поперечных волн на струне
Выведем волновое уравнение для поперечных бегущих волн в непрерывной среде. В качестве модели среды рассмотрим непрерывную однородную
струну, левый конец которой находится в точке x = 0.
21.
21Воздействуем на конец струны поперечной гармонической силой. Рассмотрим вертикальное смещение U короткого отрезка струны, который можно считать простым гармоническим осциллятором. Вертикальные смещения
U этого осциллятора изменяются в зависимости от времени t и координаты
x. Волновое уравнение связывает смещение U с t и x. Будем считать поперечные волны на струне плоскополяризованными, т. е. смещения струны проис~ перпендикулярен оси
ходят только в плоскости (x, U ), а вектор смещения U
x в любой момент времени. Тогда процесс колебания можно описать одной
функцией U (x, t), характеризующей вертикальное перемещение струны.
Пусть линейная плотность струны равна ρ, а натяжение вдоль струны —
N . Полагаем величину натяжения постоянной величиной, не зависящей от
смещения U и координаты x.
Рисунок 1.11 — Струна под воздействием поперечной силы
Рассмотрим участок струны длиной
s
ds =
1+
∂U
∂x
2
dx.
(1.12)
На одном конце элемента действует натяжение N , направленное под
углом θ к оси x, на другом — под углом θ + dθ (см. рисунок 1.11). Если
∂U
величина
мала, то
∂x
2
∂U
1.
∂x
22.
22Можем считать, что согласно (1.12) ds ≈ dx, и тогда масса элемента струны
будет:
m = ρds ≈ ρdx.
(1.13)
Запишем уравнение элемента струны, используя второй закон Ньютона:
∂ 2U
F =m 2
∂t
(1.14)
Сила, действующая на элемент ds в направлении положительных смещений U , будет равна:
F = N [sin(θ + dθ) − sin θ] .
(1.15)
Для малых значений угла θ справедливо соотношение
∂U
.
sin θ ∼
= tg θ =
∂x
Следовательно, можно записать:
F =N ·
∂U
∂x
−
x+dx
∂U
∂x
(1.16)
.
x
Таким образом, из (1.14) и (1.15) следует, что
∂ 2U
m · 2 = N · [sin(θ + dθ) − sin θ] .
∂t
Воспользуемся соотношениями (1.13) и (1.16), и перепишем верхнее выражение в виде:
∂ 2U
ρdx · 2 = N ·
∂t
∂U
∂x
−
x+dx
∂U
∂x
.
(1.17)
x
∂U
Разность в квадратных скобках равна произведению функции
на dx.
∂x
Следовательно, сила будет равна
2
∂ U
dx.
F =N
∂x2
23.
23Перепишем выражение (1.17) в виде:
∂ 2U
∂ 2U
N
dx = ρ 2 dx ⇒
∂x2
∂t
∂ 2U
ρ ∂ 2U
=
.
∂x2
N ∂t2
N
Соотношение
имеет размерность квадрата скорости v 2 . Это позволяет
ρ
переписать предыдущее уравнение в виде:
∂ 2U
1 ∂ 2U
−
= 0.
∂x2
v 2 ∂t2
(1.18)
Волновое уравнение связывает ускорение гармонического осциллятора в среде со второй производной его смещения по координате x. В этом уравнении
vф — волновая (или фазовая) скорость, с которой перемещаются плоскости
одинаковой фазы. Для данного примера
s
vф =
N
.
ρ
(1.19)
Здесь значением N определяются упругие свойства среды распространения волны, а величиной ρ — инерция среды, связанная с накоплением энергии. Связь волновой скорости со свойствами упругости среды (связанной с
накоплением потенциальной энергии в среде) и ее инерционными свойствами
(связанной с накоплением кинетической или индуктивной энергии) проявляется для всех типов волн, в том числе и для электромагнитных волн.
1.3.2
Решение волнового уравнения
Решением волнового уравнения является любая функция вида:
U = f1 (vt − x)
или
U = f2 (vt + x).
Полное решение является суперпозицией частных решений:
U = f1 (vt − x) + f2 (vt + x).
(1.20)
Покажем, что (1.20) действительно является полным решением волнового уравнения.
24.
24(Решение волнового уравнения)
Рисунок 1.12 — Решение уравнения д’Аламбера для треугольного импульса
Обозначим через f10 производную функции f1 по аргументу ct − x. Тогда
производные по координате:
∂U
/
= −f1 (vt − x),
∂x
∂ 2U
//
= f1 (vt − x).
2
∂x
Производные по времени:
∂U
/
= vf1 (vt − x),
∂t
∂ 2U
//
= v 2 f1 (vt − x).
2
∂t
Подставив значения частных производных по x и по t в волновое уравнение
(1.18), легко убедится, что функция f1 (vt − x) действительно является его
решением. Аналогично можно убедится в том, что функция f2 (vt + x) также
является решением уравнения (1.18).
Эквивалентны следующие формы записи функции U = f (vt − x):
h
2π
x i
U (x, t) = A · sin
· (vt − x) = A · sin 2π · f t −
=
λ
λ
h
x i
= A · sin ω · t −
= A · sin (ωt − kx) .
v
Здесь используются следующие соотношения:
ω=
h рад i
2π · v
= 2π · f — циклическая (круговая) частота
,
λ
сек
f — линейная частота Гц, сек−1 .
(1.21)
25.
252π
ω
= — волновое число.
λ
v
Часто бывает удобно использовать функцию U (x, t) в виде
k=
(1.22)
U = A · ei(ωt−kx) .
1.3.3
Энергия поперечных колебаний струны
Найдем выражение для энергии поперечных колебаний струны. В общем
случае энергия есть
W = K + P,
(1.23)
где K — кинетическая и P — потенциальная энергия.
Найдём кинетическую энергию струны. Элемент струны dx, движущий∂U
, обладает кинетической энергией
ся со скоростью v =
∂t
2
1 2 1
∂U
mv = ρ(x)dx
2
2
∂t
(m = ρdx).
Кинетическая энергия всей струны равна
1
K =
2
Zl
2
∂U (x, t)
ρ(x)
dx.
∂t
(1.24)
0
Теперь запишем выражение для потенциальной энергии струны.
Потенциальная энергия поперечных колебаний струны, имеющей при t =
t0 форму U (x, t0 ) = U0 (x), равна работе, которую надо совершить, чтобы
струна перешла из положения равновесия в положение U0 (x). Пусть функция
U (x, t) дает профиль струны в момент t, причем
U (x, 0) = 0,
U (x, t0 ) = U0 (x).
Элемент dx под действием равнодействующей сил натяжения
∂U
∂ 2U
∂U
N
−N
=N
dx
∂x x+dx
∂x x
∂x2
26.
26∂U (x, t)
за время dt проходит путь
dt.
∂t
Работа, производимая всей струной за время dt, равна
l
Z
0
∂ 2 U ∂U
Zl
l
∂U ∂U
∂U ∂ 2 U
− N0
N0 2
dt = N0
dx dt =
∂x ∂t
∂x ∂t 0
∂x ∂x∂t
0
(1.25)
l
Z
l
2
1d
∂U
∂U ∂U
dt.
= −
N0
dx + N0
2 dt
∂x
∂x ∂t 0
0
Интегрируя (1.25) по t от 0 до t0 , получаем:
1
−
2
Zl
N0
∂U
∂x
Zt0
t0
2
+
dx
0
0
=−
1
2
Zl
0
N0
l
∂U ∂U
dt =
N0
∂x ∂t 0
∂U (x, t0 )
∂x
Zt0
2
dx +
0
0
(1.26)
l
N0
∂U ∂U
dt.
∂x ∂t 0
Определим физический смысл последнего члена в правой части равенства (1.26).
∂U
- N0
— величина натяжения струны на конце x = 0.
∂t
x=0
-
∂U (0, t)
dt — перемещение конца x = 0.
∂t
Интеграл
Zt0
∂U ∂U
N0
dt
∂x ∂t x=0
0
представляет работу, которую надо затратить на перемещение конца x = 0.
Аналогично при x = l.
Если концы струны закреплены, то работа на концах будет равна нулю
(0,t)
(при этом U (0, t) = 0 и ∂U∂t
= 0). При перемещении такой струны из положения равновесия U = 0 в положение U0 (x) работа не зависит от способа
перевода струны в это положение и равна потенциальной энергии в момент
27.
27t = t0 с обратным знаком.
1
P=
2
Zl
N0
∂U0 (x)
∂x
2
(1.27)
dx.
0
Теперь можем записать выражение для полной энергии струны, совершающей поперечные колебания:
1
W =K +P =
2
2
2 #
Zl "
∂U
∂U
N0
+ ρ(x)
dx.
∂x
∂t
0
Если струна однородна (ρ(x) = const) и величина натяжения в каждой
точке не меняется со временем (N0 = N ), тогда
W =
1
2
Zl "
0
N
∂U
∂x
2
+ρ
∂U
∂t
2 #
dx.
(1.28)
28.
28ТЕМА 2
Основные понятия
2.1
Фазовая скорость
Очень важной величиной для гармонической бегущей волны является
фазовая скорость. Она характеризует скорость, с которой возмущение передается по системе осцилляторов.
(Понятие волнового движения)
Рисунок 2.1 — К определению фазовой скорости
Таким образом, фазовую скорость можно выразить как:
vф =
dx
.
dt
(2.1)
Определим фазовую функцию ϕ(x, t) волны как аргумент волновой функции sin(ωt − kx) , т. е.
ϕ = ωt − kx.
(2.2)
Соотношение между x и t для точек постоянной фазы определяется из
равенства полного дифференциала от фазы нулю.
dϕ =
∂ϕ
∂t
!
dt +
∂ϕ
∂x
!
dx = ωdt − kdx = 0.
29.
29Исходя из данного соотношения, с учетом (2.1) имеем
vф =
dx
dt
=
ω
k
(2.3)
.
Учитывая известные соотношения:
ω=
2π
1
2π
, f = , ω = 2π · f, k =
,
T
T
λ
получаем несколько выражений для фазовой скорости:
vф =
2.2
ω
k
=λ·f =
λ
T
.
(2.4)
Импеданс
При описании бегущих волн величиной, характеризующей среду, является фазовая скорость. Выражение для фазовой скорости в случае волн на
струне является комбинацией параметров N и ρ, определяющих возвращающую сипу и инерцию (смотри уравнение (1.19)).
Бегущие волны переносят энергию и импульс. Величиной, характеризующей скорость, с которой энергия распространяется вдоль среды при возбуждении ее внешней силой, является характеристический импеданс (или просто
импеданс, или волновое сопротивление) для волн в среде.
Рисунок 2.2 — Подключение «передатчика» к бесконечной струне в точке с
координатой x = 0
Получим выражение в случае волн на непрерывной струне, на которую
в её начале (точка x = 0) действует поперечная гармоническая сила. Будем
считать, что струна в точке x = 0 возбуждается «передатчиком». В состоянии равновесия поперечная составляющая силы, действующая со стороны на
«передатчик», отсутствует.
30.
30Рисунок 2.3 — Излучение «передатчиком» волн, бегущих по бесконечной
струне
При возбуждении волны возникает поперечная составляющая силы, с
которой левый конец струны в точке x = 0 действует на «передатчик»:
sin Θ
= N0 tg Θ = N0
∂U
.
(2.5)
cos Θ
∂x
Если струна бесконечной длины, в ней распространяются бегущие волны:
FU = N sin Θ = N cos Θ
U = U0 cos(ωt − kx).
Продифференцируем это выражение:
∂U
∂x
= kU0 sin(ωt − kx),
∂U
∂t
= −ωU0 sin(ωt − kx).
(2.6)
ω
Воспользуемся выражением для фазовой скорости в виде vФ = , тогда
k
из (2.6) следует:
∂U
1 ∂U
=−
.
∂x
vФ ∂t
Подставляя это выражение в (2.5) для поперечной составляющей силы,
имеем:
N0 ∂U
FU = −
.
vФ ∂t
∂U
Величина
— поперечная скорость струны в точке её возбуждения. При
∂t
«излучении» бегущих волн сила, с которой среда (струна) воздействует на
31.
31передатчик, является демпфирующей силой. Она обратно пропорциональна
фазовой скорости распространения волн в среде.
N0
Величину Z =
называют характеристическим импедансом среды.
vФ
Для струны импеданс является поперечным импедансом и равен:
Z=
N
v
=
поперечная сила
поперечная скорость
.
s
Для поперечных бегущих волн на струне vФ =
N0
ρ0
, поэтому
N0 p
Z=
= N0 ρ0 = ρ0 vФ .
vФ
Самым важным свойством демпфирующей силы является то, что она вызывает поглощение (рассеяние) энергии. В рассматриваемом примере со струной излучаемая «передатчиком» мощность равна произведению поперечной
силы, с которой передатчик воздействует на струну в точке x = 0, на поперечную скорость струны в этой точке.
Для мгновенной мощности в случае бегущих волн
2
∂U ∂U
∂U
P (t) = Z
=Z
.
∂t ∂t
∂t
(2.7)
Мощность P (t) можно выразить через поперечную силу, действующую
на выходной зажим «передатчика»:
2
2
∂U
vФ
∂U
1
∂U
∂U
· −vФ
=
−N0
=
−N0
.
P (t) = −N0
∂x
∂x
N0
∂x
Z
∂x
(2.8)
Выражения (2.7) и (2.8) эквивалентны.
Излучаемая передатчиком в точке x = 0 мощность равна энергии, переносимой волной в единицу времени в направлении распространения. В произвольной точке x:
2
1
∂U (x, t)
P (x, t) =
−N0
.
(2.9)
Z
∂x
Мощность волны пропорциональна квадрату ее напряженности (амплитуды).
32.
32Рассмотрим гармоническую волну, записав ее в виде:
U = U0 cos(ωt − kx + ϕ).
(2.10)
Мгновенное значение мощности P (t) пропорционально U 2 . Выберем коэффициент пропорциональности равным 2 (это достигается соответствующим
выбором единиц измерения величины U ). Тогда
P (t) = 2U 2 = 2U02 cos2 (ωt − kx + ϕ) = U02 [1 + cos (2(ωt − kx + ϕ))] . (2.11)
Из (2.11) видно, что мгновенная мощность изменяется во времени с удвоенным значением круговой частоты — 2ω. Среднее значение cos (2(ωt − kx + ϕ))
равно нулю. Поэтому средняя мощность равна P̄ = U02 . Мгновенная мощность изменяется от 0 до 2P с частотой 2ω.
Мощность волны — это величина, имеющая направление. Мощность волны P (t) в направлении +x равна мощности волны — P (t) в направлении −x.
2.3
Отражение и прохождение волн
Большинство задач, решаемых в теории и практике распространения
волн, связано с изучением распространения волн в неоднородных средах. Одной из самых простых задач является исследование процессов при падении
волны на границу раздела двух сред с различными свойствами. Рассмотрим
поведение бегущей волны на границе раздела двух сред, воспользовавшись
ранее введенным понятием импеданса.
Передатчик, воздействующий на открытую среду, возбуждает бегущие
волны. Со стороны среды на выходные зажимы передатчика действует сила сопротивления, пропорциональная характеристическому импедансу. Если
заменить антенну радиопередатчика ее активным эквивалентным сопротивлением, каких-либо изменении в работе передатчика мы не обнаружим. Т. е.
передатчик этой замены не «чувствует». В случае струны мы можем нагрузить «передатчик», возбуждающий ее, непосредственно на поршень, демпфирующий колебания на выходе «передатчика». В этом случае на выход
передатчика будет действовать точно такая же сила сопротивления, как и
в случае присоединения его к бесконечной струне. Это возможно в случае
33.
33равенства импедансов струны и ее эквивалента (демпфирующего поршня):
p
Zэкв = Z = N0 ρ0 .
В этом случае можно считать, что импеданс нагрузки согласован с импедансом среды распространения (струны).
Нас будет интересовать вопрос, как отреагируют волны, распространяющиеся в среде, на резкое изменение импеданса в какой-либо точке.
Рассмотрим бесконечно простирающуюся от x = −∞ до x = +∞ струну,
состоящую из двух частей с различными линейными плотностями ρ1 и ρ2 ,
соединенных в точке x = 0. Натяжение N считаем неизменным по всей длине
струны. Волновые скорости и импедансы для отрезков 1 и 2 различаются и
равны:
s
s
N
N
, v2 =
, Z1 = ρ1 v1 , Z2 = ρ2 v2 .
v1 =
ρ1
ρ2
Если бы выполнялось условие Z1 = Z2 , то волна не почувствовала бы
наличие границы, разделяющей среды в точке x = 0. В интересующем нас
случае Z1 6= Z2 можно представить распространение волны на струне следующим образом. В точке x = −∞ находится «передатчик», генерирующий
волну, бегущую в сторону положительных значений x. Запишем уравнение
этой волны, считая её гармонической, в форме:
Uпад (x, t) = U0 cos(ωt − kx).
В точке x = 0 струна подсоединена к эквивалентной нагрузке с импедансом Z2 . Уравнение волны в точке x = 0:
Uпад (0, t) = U0 cos(ωt).
В случае неравенства импедансов отрезка N1 струны и нагрузки (отрезок
N2 ) в точке x = 0 на струну N1 действует избыточная сила
Fизб = Z1
∂Uотр (0, t)
,
∂t
34.
34приводящая к распространению волны в направлении −x (т. е. к отражению).
В непосредственной близости от точки x = 0 смещение струны справа и слева
от границы раздела равны, т. е. должно выполняться условие:
Uпад |x=0 + Uотр |x=0 = Uпрох |x=0 .
(2.12)
Здесь Uпад , Uотр , Uпрох — амплитуды падающей, отраженной и проходящей
волн.
Запишем эти волны в виде:
Uпад = U0 cos(ωt − k1 x),
Uотр = U1 cos(ωt + k1 x),
(2.13)
Uпрох = U2 cos(ωt − k2 x).
Отсюда получим условие для амплитуд на границе раздела двух сред:
(2.14)
U0 + U1 = U2 .
Другим условием, выполняющимся в точке x = 0, является непрерыв∂U
ность поперечной силы N
. Согласно этому условию:
∂x
N
∂
∂
[U0 cos(ωt − k1 x) + U1 cos(ωt + k1 x)] = N
U2 cos(ωt − k2 x),
∂x
∂x
или
−U0 N k1 sin(ωt − k1 x) + k1 U1 sin(ωt + k1 x) = −U2 k2 N sin(ωt − k2 x).
Учитывая, что
k1 =
ω
ω N
; k2 = ;
= ρ1 v1 = Z1 ;
v1
v2 v1
N
= ρ2 v2 = Z2 ,
v2
в точке x = 0 имеем
Z1 (−U1 + U0 ) = Z2 U2 .
(2.15)
35.
35Из уравнений (2.14) и (2.15) находим коэффициент отражения (по амплитуде):
Uотр
Z1 − Z2
R12 =
=
(2.16)
Uпад
Z1 + Z2
и коэффициент пропускания:
T12 =
Uпрох
2Z1
=
.
Uпад
Z1 + Z2
(2.17)
Эти коэффициенты не зависят от частоты ω, действительны и не вносят фазовых сдвигов. Значения R и T полностью определяются отношениями
импедансов. Точно таким же выражением определяются коэффициенты отражения и прохождения для других типов волн.
2.3.1
Два случая отношения импедансов граничащих сред
Рассмотрим два случая отношения импедансов.
Первый случай: если Z2 Z1 , то отношение импедансов будет стремиться к бесконечности:
Z2
→ ∞.
Z1
Тогда коэффициент отражения будет равен
R12 =
Z1 − Z2
−Z2
≈
= −1.
Z1 + Z2
Z2
В этом случае при сложении падающей и отраженной волн смещение
(амплитуда) в точке x = 0 будет равно нулю. Падающая волна отражается
полностью, при этом её фаза изменяется на π, как это показано на рисунке 2.4.
Случай, показанный на рисунке 2.4, соответствует возбуждению стоячих
волн. Положительный импульс в падающей волне становится отрицательным
после отражения. Сила, действующая на струну в точке x = 0, в два раза
больше, чем при полном согласовании. Избыточная сила затрачивается на
образование отраженной волны с амплитудой, равной по величине, но противоположной по знаку амплитуде падающей волны.
36.
36(Отражение)
Рисунок 2.4 — Отражение падающей волны при R12 = −1 (Z2 Z1 )
Второй случай: если Z2 Z1 , то отношение импедансов будет стремиться к нулю:
Z2
→ 0.
Z1
Тогда коэффициент отражения будет равен
R12 =
Z1 − Z2
Z1
≈
= +1.
Z1 + Z2
Z1
В этом случае не наблюдается изменения фазы волны при её отражении.
Отражение импульса от свободного конца струны иллюстрирует рисунок 2.5
Рассмотрим, что происходит с энергией волны при ее падении на границу раздела сред с разными импедансами. Ясно, что скорость поступления
энергии на границу x = 0 равна энергии, переносимой волной в единицу времени. Падающая на границу энергия уносится отраженной и преломленной
волнами. Если рассматривать единичный отрезок струны как гармонический
осциллятор, совершающий колебания около равновесного положения с частотой ω волны, то он обладает энергией
1
2
E = ρω 2 Uпад
.
2
37.
37(Отражение)
Рисунок 2.5 — Отражение падающей волны при R12 = +1 (Z2 Z1 )
Скорость переноса энергии вдоль струны определяется произведением E
на скорость распространения волны:
1
1
2
2
ρ1 c1 ω 2 Uпад
= Z1 ω 2 Uпад
.
2
2
Скорость уноса энергии:
!
2
2
U
U
1
1
1
прох
отр
2
2
2
=
Z1 ω 2 Uотр
+ Z2 ω 2 Uпрох
=
ω 2 Uпад
Z1 2 + Z2 2
2
2
2
Uпад
Uпад
#
"
2
2
1 2 2
(Z1 − Z2 )
(2Z1 )
1 2
2
=
ω Uпад
ω Z1 Uпад
.
Z1
+
Z
=
2
2
2
2
2
(Z1 + Z2 )
(Z1 + Z2 )
Таким образом было показано, что вся энергия, переносимая падающей волной к границе раздела двух сред, уносится от нее отраженной и преломленной
волнами. При согласовании импедансов (Z1 = Z2 ) энергия не отражается.
2.3.2
Согласование импедансов двух сред
Целью согласования импедансов является создание режима бегущей волны при распространении ее из одной среды в другую. Например, в радиотехнике такая задача возникает при подключении передатчиков и приемников
при помощи фидеров к антеннам, либо подключении различных измеритель-
38.
38ных приборов к испытываемой аппаратуре и т. д. Возможно несколько путей
решения этой задачи.
Мы рассмотрим один из вариантов, пригодный для согласования импедансов в узкой полосе частот. Способ состоит в ведении между средами с
импедансом Z1 и Z3 дополнительной среды с импедансом Z2 . Необходимо
определить значение Z2 и толщину (протяжность) согласующей среды (l).
Рисунок 2.6 — Схема согласования импедансов двух сред в узком диапазоне
частот
Пусть среда 1 простирается от x = −∞ до x = 0 (см. рисунок 2.6), среда
3 от x = l до x = +∞. Между ними располагается согласующая среда 2 с
импедансом Z2 . Согласование будем проводить для волн с частотой ω.
Запишем выражение для падающей волны:
Uпад (x, t) = U0 cos(ωt − k1 x).
(2.18)
Эта волна частично отражается в точке x = 0, т. к. здесь существует скачок
импеданса. Амплитуда отраженной волны равна:
Uотр (0, t) = R12 U0 cos(ωt + k1 x).
(2.19)
На границе x = 0 волна (2.18) частично преломляется в среду 2 с коэффициентом T12 , отражается на границе x = l с коэффициентом отражения R23 ,
пройдя по среде 2 расстояние 2l, преломляется на границе x = 0 с коэффи-
39.
39циентом T21 . Амплитуда этой волны, прошедшей в среду 1, равна:
Uотр (l, t) = T12 R23 T21 U0 cos(ωt + k1 x − 2k2 l).
(2.20)
Если коэффициенты отражения малы в сравнении с единицей (а это
справедливо, если импедансы Z1 , Z2 , Z3 мало отличаются друг от друга),
можно пренебречь вкладом многократно отраженных волн и ограничиться
рассмотрением только первых двух отражений. Если значения R12 и R21 малы, то можно считать, что
2
T12 T21 = (1 − R12 ) (1 − R21 ) = 1 − R12
≈ 1.
Отраженные в среду 1 волны (2.18) и (2.20) будут интерферировать, и результирующая амплитуда волны будет равна:
Uотр ≈ R12 U0 cos(ωt + k1 ) + R23 U0 cos(ωt + k1 − 2k2 l).
(2.21)
Путем подбора значения импеданса Z2 можно добиться равенства коэффициентов отражения R12 = R23 . Учитывая, что
R12 =
Z2 − Z3
Z1 − Z2
, R23 =
,
Z1 + Z2
Z2 + Z3
для Z2 получаем:
Z2 =
p
Z1 Z3 .
(2.22)
При этом отраженную волну в среде можно представить в виде:
Uотр = R12 U0 [cos(ωt + k1 x) + cos(ωt + k1 x − 2k2 l)] = 0.
(2.23)
Значение Uотр равно нулю, если 2k2 l = π. Таким образом, волна в согласующей среде 2 должна пройти расстояние
2l =
λ
2
и протяженность этой среды должна быть равна:
l=
λ
.
4
(2.24)
40.
40Рассмотренный способ согласования пригоден лишь для узкого интервала частот. Согласования в широкой полосе частот можно добиться с помощью
устройства (среды), в котором импеданс монотонно изменяется на длине l, а
на длине, равной четверти длины любой из передаваемых волн, изменяется
на очень маленькую величину.
2.4
Стоячие волны
В реальных средах не всегда удается добиться согласования импедансов
при распространении волны из одной среды в другую. Поэтому часто энергия
отражается на границе. Посмотрим, что произойдет, если импеданс второй
среды равен бесконечности. При этом падающая волна полностью отражается с изменением фазы на ∆ϕ = π радиан. Поэтому амплитуды отраженной
и падающей волн связаны соотношением:
Uпад = −Uотр .
(2.25)
В результате сложения падающей и отраженной волн образуется стоячая волна. Для примера рассмотрим струну длиной l, жестко закрепленную на концах.
Пусть в сторону положительных x распространяется волна:
U = Uпад = U0 ei(ωt−kx) ,
(2.26)
а в сторону отрицательных x:
U = Uотр = U0 ei(ωt+kx) .
(2.27)
Смещение в любой точке будет равно:
U = U0 eiωt (e−ikx − eikx ) = −2iU0 eiωt sin(kx).
Подставим решение (2.28) в волновое уравнение
1 ∂ 2U
∂ 2U
− 2 · 2 = 0.
∂x2
v
∂t
(2.28)
41.
41Возьмём производные по t:
∂U
= iωU0 eiωt (e−ikx − eikx ),
∂t
∂ 2U
= −ω 2 U0 eiωt (e−ikx − eikx ) = −ω 2 U,
2
∂t
отсюда:
∂ 2U
∂ 2U ω2
+ 2U =
+ k 2 U = 0.
(2.29)
2
2
∂x
v
∂x
Мы получили стационарное (не зависящее от времени) волновое уравнение, описывающее стоячие волны.
На закрепленных концах струны амптитуда равна нулю, т. е. U = 0 при
x = 0 и x = l. Поэтому из (2.28) следует
ω
ωl
sin(kl) = sin
l = 0 т. е.
= n · π.
v
v
На струне в данном случае могут существовать колебания с частотами
ωn =
nπv
;
l
fn =
nv
2l
Это так называемые нормальные частоты, соответствующие нормальным
модам.
Если n > 1, то на струне будет ряд точек, остающихся неподвижными.
Их положение определяется из уравнения:
sin
ωn x
nπx
nπx
= sin
= 0, или
= mπ
v
l
l
(m = 0 . . . n).
Это так называемые узловые точки или узлы (см. рисунок 2.7).
2.4.1
Коэффициент стоячей волны
Если отражение от границы среды не полное, то бегущие в разных направлениях волны не точно компенсируют друг друга и не образуют идеальных узлов с нулевой амплитудой. В этом случае вводится понятие коэффициент стоячей волны (КСВ).
42.
42(Стоячая волна)
Рисунок 2.7 — Стоячая волна. Нормальные моды. Узлы
Если выразить амплитудный коэффициент отражения следующим образом,
Uпад
= r,
Uотр
максимальная амплитуда волны будет равна (Uпад + Uотр ), минимальная —
(Uпад − Uотр ), тогда коэффициент стоячей волны будет равен
КСВ =
1+r
Uпад + Uотр
=
.
Uпад − Uотр
1−r
(2.30)
В режиме стоячей волны полная энергия, переносимая в одном направлении, в точности равна энергии, переносимой в противоположном направлении. Поэтому полный поток энергии (т. е. энергия, переносимая в единицу
времени через единичную площадь) в стоячей волне равен нулю.
2.5
Дисперсия
Ранее мы получили, что фазовая скорость определяется характеристиками среды
s
N
vФ =
.
ρ
43.
43С другой стороны получили, что
vФ =
dx
dt
=
ω
k
.
Таким образом можем записать
s
ω
N
= .
ρ
k
Отсюда получаем, что
s
ω=
N
k.
ρ
(2.31)
Данное равенство даёт соотношение между частотой и волновым числом нормальных мод струны.
Выражение, определяющее частоту как функцию волнового числа, называется дисперсионным соотношением.
2.5.1
Закон дисперсии для реальной струны пианино
Пространственная конфигурация мод реальной струны совпадает с кон1
1
фигурацией мод совершенно упругой струны: λ1 = 2l, λ2 = λ1 , λ3 = λ1 ,
2
3
. . . , так как граничные условия в обоих случаях одни и те же.
Однако наличие изгибной жесткости, отличающей реальную струну от
идеальной, приводит к дисперсии, в результате чего поперечные волны различной длины распространяются вдоль струны с различными скоростями.
Поэтому обертоны высших порядков имеют частоты, прогрессивно завышенные относительно гармонического ряда.
Отсюда возникают такие дефекты звучания музыкального инструмента,
как «металлические» басы и «стеклянные» дисканты фортепьяно. На рисунке 2.8 показаны значения коэффициентов негармоничности для струн пианино «Ноктюрн»1 , поизводства ленинградской фабрики «Красный Октябрь».
1
А. Аскенфелт, А. С. Галембо. Исследования спектральной негармоничности музыкального звука с помощью алгоритмов экстракции высоты //Акустический журнал. — 2000. — Т. 46, №2. — С. 157–169.
44.
44Рисунок 2.8 — Измеренные значения коэффициента негармоничности для
струн пианино «Ноктюрн»
В данном случае дисперсионное соотношение можно записать как:
p
fn = nf0 1 + n2 B,
где fn — частота n-ой моды собственных колебаний; f0 — частота основного тона для идеально гибкой струны; B — коэффициент негармоничности,
который равен:
π 3 Y r3
B=
64N L
Y — модуль Юнга; N — натяжение; L — длина и r — радиус струны.
Рассмотренный в этом параграфе случай называется материальной дисперсией, т. к. здесь дисперсия связана с материальными свойствами среды
распространения. В следующих лекциях мы рассмотрим случаи волновой и
временно́й дисперсий.
45.
452.6
Групповая скорость
Во всех рассмотренных ранее случаях под скоростью распространения
волн мы понимали фазовую скорость, т. е. скорость, с которой распространяется поверхность одинаковых фаз.
Ранее мы определили, что фазовая скорость
vф =
ω
.
k
(2.32)
В общем случае синусоидальные волны различных частот имеют различные фазовые скорости и, следовательно, различные значения волнового
параметра (числа)
2π
k= .
(2.33)
λ
Соотношение ω = f (k) между частотой и волновым числом (или периодом и длиной волны), называемой дисперсионным соотношением, приведено
на рисунке 2.9.
Рисунок 2.9 — График бездисперсионной моды
В точке с координатами (ω, k) кривой ω = f (k) волновая скорость будет
равна
ω
vф = ,
k
т. е. определятся наклоном прямой, проведенной из начала координат в точку
с координатами (ω, k).
46.
46Если функция ω = f (k) имеет вид прямой линии, проведённой из начала
координат (как показано на рисунке 2.9), то фазовая скорость одинакова для
волн любой частоты. Такая мода называется бездисперсионной.
2.6.1
Бездисперссионная мода
Рассмотрим пакет из двух волн с одинаковыми амплитудами, но разными
частотами ω1 и ω2 . Полагаем, что разность частот ∆ = |ω2 − ω1 | мала. Будем
описывать волны на частотах ω1 и ω2 в форме (см. рисунок 2.10):
U1 = U0 cos(ω1 t − k1 x);
(2.34)
U2 = U0 cos(ω2 t − k2 x).
Рисунок 2.10 — Две синусоидальных волны с одинаковыми амплитудами
(U0 = 1) и близкими частотами (∆ω = ω1 − ω2 = 0,1)
Сложим колебания, применив тригонометрическое преобразование для
суммы косинусов двух углов:
α+β
cos α + cos β = 2 cos
2
α−β
cos
2
47.
47U = U1 + U2 = U0 cos (ω1 t − k1 x) + U0 cos (ω2 t − k2 x) =
(ω1 t − k1 x) + (ω2 t − k2 x)
(ω1 t − k1 x) − (ω2 t − k2 x)
= 2U0 cos
cos
=
2
2
(ω1 t + ω2 t) − (k1 x + k2 x)
(ω1 t − ω2 t) − (k1 x − k2 x)
= 2U0 cos
cos
=
2
2
k1 + k2
k1 − k2
ω1 − ω2
ω1 + ω2
t−
x cos
t−
x .
= 2U0 cos
2
2
2
2
Для суммарной волны окончательно получили:
ω1 + ω 2
k1 + k2
ω1 − ω2
k1 − k2
U = 2U0 cos
t−
x cos
t−
x .
2
2
2
2
Рисунок 2.11 — Суммарная волна с частотой
ω 1 − ω2
и амплитудой, равной 2U0
2
(2.35)
ω1 + ω2
, огибающей с частотой
2
Из рисунка 2.11 видно, что амплитуда суммарной волны изменяется значительно медленнее с изменениями t и x, чем амплитуда «заполняющей»
волны. При этом вспомним, что разность частот мы обозначили через ∆ω, а
разность волновых чисел через ∆k. Следовательно, выражение (2.35) можно
рассматривать как уравнение плоской волны с амплитудой
∆ω
∆k
U (t, x) = 2U0 cos
t−
x
2
2
.
(2.36)
48.
48Результирующая амплитуда получается в результате сложения, следовательно, будут максимумы и минимумы амплитуды. Максимум амплитуды будет
определяться условием
∆k
∆ω
t−
xmax = ±mπ,
2
2
где m = 1, 2, . . . , xmax — координата максимума амплитуды.
Каждый из этих максимумов можно рассматривать как центр соответствующей группы волн. Решив это уравнение относительно xmax , получим:
xmax =
∆ω
t + const;
∆k
(const = 2πm).
Таким образом, скорость распространения суммарной волны (волнового пакета) равна
∆ω
— групповая скорость.
(2.37)
vгр =
∆k
Если среда распространения не имеет дисперсии, т. е.
vф =
ω1
k1
=
ω2
k2
,
то фазовая скорость совпадает с групповой
vф = vгр .
Если скорости отдельных частотных составляющих различаются, то одна из них будет опережать другую. При этом форма огибающей не будет
сохранятся в процессе распространения.
2.6.2
Дисперсионная мода
Рассмотрим распространение сигнала посредством дисперсионной моды.
В общем случае волну с модулированной амплитудой можно представить в
виде произведения (свертки) низкочастотного импульса с частотой Ω и высокочастотной волны с частотой ω0 (обычно эту волну назвают несущей).
Результат умножения этих двух волн будет (см. рисунок 2.12):
Um (t) = U0 cos(Ωt) cos(ω0 t).
(2.38)
49.
49Рисунок 2.12 — Свертка высокочастотного колебания и низкочастотного импульса
Максимум интенсивности приходится на центр группы волн. Поэтому
скорость переноса энергии равна групповой скорости.
Перепишем выражение (2.38) в виде:
Um (t) =
1
[cos (ω0 + Ω) t + cos (ω0 − Ω) t] .
2
При передаче составляющих с круговыми частотами ω0 + Ω и ω0 − Ω
посредством дисперсионной моды они будут распространятся с различными
скоростями. Обозначим через k0 волновой параметр составляющей с частотой
ω0 . Наклон касательной к кривой ω = f (k) в точке ω = ω0 будет равен
(смотри рисунок 2.13):
∆Ω
S=
.
|∆k|
50.
50Рисунок 2.13 — Дисперсионная кривая для амплитудно модулированной волны
Таким образом, приближенные значения k− и k+ для частотных составляющих ω0 − Ω и ω0 + Ω будут равны:
Ω
,
S
Ω
k+ = k(ω0 + Ω) ≈ k0 + .
S
k− = k(ω0 − Ω) ≈ k0 −
После прохождения волнами расстояния x их произведение U (x, t) будет равно:
1
Ωx
Ωx
U (x, t) =
cos (ω0 + Ω) t − k0 x −
+ cos (ω0 − Ω) t − k0 x +
=
2
S
S
h
1n h
x i
x io
=
cos (ω0 t − k0 x) + Ω t −
+ cos (ω0 t − k0 x) − Ω t −
.
2
S
S
Это выражение можно переписать в виде:
h
x i
U (x, t) = cos Ω t −
cos [ω0 t − k0 x] .
S
(2.39)
Из выражения (2.39) следует, что фазовая скорость несущей частоты
равна
ω0
vф = .
k0
51.
51Модулирующая волна cos(Ωt) движется с групповой скоростью
vгр =
∆ω
.
∆k
В пределе выражение для групповой скорости примет вид:
vгр =
dω
.
dk
(2.40)
Это так называемая групповая скорость, равная скорости распространения
максимальной энергии волнового пакета.
Выражение (2.40) справедливо для центра группы произвольного числа
волн. Выражению для групповой скорости можно придать другой вид. Т.к
ω = vф k, следовательно
vгр =
Выразим
dvф
dk
dvф
d(vф k)
= vф + k
.
dk
dk
через длину волны λ:
dvф dλ
2π dλ
2π
λ
dvф
=
· ; λ=
;
=− 2 =− .
dk
dλ dk
k
dk
k
k
Таким образом,
dvф
dk
=−
dvф λ
· , и тогда
dλ k
vгр = vф − λ
dvф
.
dλ
(2.41)
Из выражения (2.41) следует, что в дисперсионной среде, в зависимости от
dvф
знака производной
, групповая скорость может быть больше или меньше
dλ
фазовой. Дисперсионные кривые для всех возможных случаев показаны на
рисунке 2.14.
Максимум интенсивности приходится на центр группы волн. Поэтому
скорость переноса энергии равна групповой скорости.
Рассмотрим распространение волнового пакета, введенного выражением (2.38) и представленного на нижней панели рисунка 2.12, для различных
типов дисперсионных кривых, показанных на рисунке 2.14.
52.
52Рисунок 2.14 — Дисперсионные кривые. Прямая 1 — бездисперсионная мода.
dvф
dvф
Прямая 2 —
> 0; vгр < vф — нормальная дисперсия. Прямая 3 —
< 0;
dλ
dλ
vгр > vф — аномальная дисперсия.
Бездисперсионная мода
Бездисперсионная мода соответствует прямой 1 на рисунке 2.14. В этом
случае групповая скорость будет равна фазовой, т. е.
vгр = vф .
Данный случай рассмотрен на рисунке 2.15.
(Бездисперсионная мода)
Рисунок 2.15 — Бездисперсионная мода. Круглым синим маркером отмечена фазовая скорость распространения несущей волны, имеющей частоту ω0 .
Красным треугольным маркером отмечена групповая скорость распространения волнового пакета
53.
53Из рисунка хорошо видно, что скорость переноса энергии волной совпадает с фазовой скоростью.
Нормальная дисперсия
Случай нормальной дисперсии, который соответствует прямой 2 на риdvф
сунке 2.14. Здесь
> 0, т. е. групповая скорость будет меньше фазовой:
dλ
vгр < vф .
Данный случай рассмотрен на рисунке 2.16. Как видно из рисунка 2.16, при
(Нормальная дисперсия)
Рисунок 2.16 — Случай нормальной дисперсии. Обозначения соответствуют
рисунку 2.15
распространении волны в её «хвостовой» части возникают всё новые максимумы, которые постепенно перемещаются вперёд, достигают головной части
и там исчезают. Таким образом, скорость распространения максимума интенсивности волнового пакета действительно меньше скорости распространения
несущей.
Такую дисперсию называют также отрицательной, поскольку с ростом
волнового числа k фазовая скорость волны убывает. Примеры сред с нормальной дисперсией — вещества, прозрачные для оптических волн, волноводы, изотропная плазма и др.
54.
54Аномальная дисперсия
Случай анормальной дисперсии, который соответствует прямой 3 на риdvф
сунке 2.14. Здесь
< 0, т. е. групповая скорость будет больше фазовой:
dλ
vгр > vф .
Данный случай представлен на рисунке 2.17.
(Аномальная дисперсия)
Рисунок 2.17 — Случай анормальной дисперсии. Обозначения соответствуют
рисунку 2.15
Как видно из рисунка 2.17, максимумы и минимумы появляются в передней части сигнала, перемещаются назад и исчезают в его хвосте, т. е. скорость распространения волнового пакета выше, чем скорость распространения несущей.
Аномальная дисперсия характерна для капиллярных волн на поверхности воды (vгр = 2vф ), для электромагнитных и акустических волн в средах с
резонансным поглощением, а также при определенных условиях — для волн
в периодических структурах (кристаллы, замедляющие системы и т. п.). При
этом возможна даже ситуация, при которой групповая скорость направлена
противоположно фазовой.
Обратные волны
Вообще говоря, скорость всегда имеет направление, т. е. скорость — это
векторная величина. Понятие скорости имеет физический смысл только в
том случае, если определено направление движения.
55.
55Как было замечено в предыдущем параграфе, при определенных условиях для волн в периодических структурах (кристаллы, замедляющие системы и т. п.) возможна ситуация, при которой групповая скорость направлена
противоположно фазовой. Волны, обладающие этим свойством, называются
обратными. Пример обратной волны приведён на рисунке 2.18.
(Отрицательная групповая скорость)
Рисунок 2.18 — Обратная волна, для случая когда |vгр | = |vф |, но при этом
vгр < 0
Нулевая групповая скорость
Частным случаем отрицательной групповой скорости может быть ситуация, когда групповая скорость будет равна нулю. Возможное развитие
подобной ситуации показано рисунке 2.19.
(Нулевая групповая скорость)
Рисунок 2.19 — Нулевая групповая скорость: vф > 0, vгр = 0
Здесь, однако, необходимо сказать, что подобные решения будут весьма
неустойчивы, т. к. развитие подобной ситуации возможно только в средах с
56.
56очень сильной дисперсией. В этом случае даже очень незначительная немонохромность либо несущей, либо модулирующей волны приведет к тому, что
групповая скорость будет отличной от нуля. Необходимо помнить, что задача генерации абсолютно монохромного излучения не решена до настоящего
времени. Даже лазерное излучение, строго говоря, нельзя считать абсолютно
монохромным.
«Медленный свет»
Все знают, что свет переносит сигналы с максимально возможной в природе скоростью, почти ∼ 300 000 км/с. Правда, в любой прозрачной среде
световые волны распространяются несколько медленней (в 1,33 раза в воде,
в 1,5–2 раза в стекле и пластмассе, в 1,0003 раза в атмосферном воздухе).
Даже в алмазе, который превосходит все природные материалы по величине коэффициента преломления, скорость света равна 125 000 км/с. Ученые
полагали, что снизить ее еще больше вряд ли возможно. Однако за последние
годы физики смогли замедлить свет . . . вплоть до полной остановки.
В 1999 году группа гарвардских ученых под руководством Лене Вестергаард Хау произвела научную сенсацию2 , сообщив, что облучение лазером почти не прозрачного сверххолодного газа (который охлаждали до температур в
несколько нанокельвин) из атомов натрия в состоянии Бозе–эйнштейновского
квантового конденсата заставляет его пропускать свет со скоростью 17 м/с,
что соответствует скорости автобуса, поднимающегося в крутую горку.
Профессор Хау и ее коллеги измеряли скорости миллисекундных лазерных вспышек, скомпонованных из монохроматических волн разной частоты.
При наложении друг на друга эти волны частично гасятся и частично усиливаются, в результате чего формируется короткий световой импульс — волновой пакет. Данный волновой пакет перемещается с групповой скоростью,
которая в общем случае не совпадает с фазовыми скоростями составляющих его волн. Бозе–эйнштейновский конденсат принадлежит к числу сред с
очень сильной дисперсией и потому может замедлить световые импульсы во
многие миллионы раз. Аналогичной способностью обладают некоторые менее
2
Hau L. V., Harris S. E., Behroozi C. H. Light speed reduction to 17 meters per second in an ultracold atomic
gas. Natire, v. 397, p. 594–598 (1999)
57.
57экзотические среды, такие как горячий атомный пар и оптические волокна,
допированные атомами эрбия.
В 2001 году ее группа на короткое время сначала полностью заморозила
свет внутри такого же конденсата, а потом высвободила его для дальнейшего
движения. Задержка составила лишь одну миллисекунду, но спустя восемь
лет гарвардские физики смогли задержать свет дольше, чем на секунду.
Замороженный свет может хранить и переносить информацию, что также доказали Лене Хау и ее сотрудники. В 2007 году они пленили лазерную
вспышку в бозе-эйнштейновском конденсате, а потом перенесли его атомы
в другой такой же конденсат. Когда его облучили лазером и сделали оптически прозрачным, он породил световой сигнал — точную копию исходного
лазерного импульса3 .
Основные свойства групповой скорости
- Групповая скорость — это скорость переноса энергии волны в среде.
- Групповая скорость не может быть выше скорости света.
- Групповая скорость может быть отрицательной.
- Групповая скорость имеет физический смысл, когда она является действительной величиной.
Это возможно, если среда обладает малым поглощением. Если не учитывать это, то можно получить физически нереальный случай превышения групповой скоростью скорости света в вакууме.
3
Алнксей Левин. Стекло, которое замедляет свет //Популярная механика. — №12. — декабрь 2012.
(http://www.popmech.ru/magazine/2012/122-issue/)
58.
58ТЕМА 3
Электромагнитные волны диапазона радиочастот
Радиоволны занимают часть спектра электромагнитных волн, ограниченную пределами 3 · 103 ÷ 3 · 1012 Гц.
В таблице 3.1 приведена классификация длин радиоволн по диапазонам
и соответствующая ей номенклатура частотных полос, принятая Международным консультативным комитетом по радио (МККР)1 в 1959 г.
Таблица 3.1 — Деление радиочастот по диапазонам
Классификация по длинам волн
Длина волны
Диапазон в свободном
Метрические
пространстве
подразделение
волн
(вакууме)
волн
в метрах
СДВ
105 ÷ 104
мериаметровые
4
3
ДВ
10 ÷ 10
километровые
СВ
103 ÷ 102
гектометровые
КВ
102 ÷ 10
декаметровые
10 ÷ 1
метровые
1 ÷ 0.1
дециметровые
УКВ
0.1 ÷ 0.01
сантиметровые
0.01 ÷ 0.001
миллимитровые
10−3 ÷ 10−4 субмиллимитровые
Классификация по частотам
Диапазон
Сокращённые
частот (исключая
буквенные
нижний и влючая обозначения
верхний предел)
полос
3 ÷ 30 кГц
30 ÷ 300 кГц
300 ÷ 3000 кГц
3 ÷ 30 МГц
30 ÷ 300 МГц
300 ÷ 3000 МГц
3 ÷ 30 ГГц
30 ÷ 300 ГГц
300 ÷ 3000 ГГц
ОНЧ
НЧ
СЧ
ВЧ
ОВЧ
УВЧ
СВЧ
КВЧ
В современной технической литературе всё чаще встречаются буквенные обозначения отдельных выделенных диапазонов радиочастот. Кодовые
буквенные обозначения были введены англичанами во время второй мировой войны для обеспечения секретности. Затем эти обозначения перешли в
открытое употребление.
Изначально для обозначения частотных диапазонов использовались буквы — P , L, S, X и K. Позднее, с началом использования новых диапазонов,
были введены буквы — C, Ku и Ka . Буквы P и K в настоящее время практически не используются. Буквенные обозначения приведены в таблице 3.2.
Ранее мы на примере волн на струне показали, что скорость распространения волн в среде определяется инерцией среды и ее упругостью, т. е.
1
Чёрный Ф. Б. Распространение радиоволн. М.: Сов. Радио. 1972.
59.
59Таблица 3.2 — Буквенные обозначения частотных диапазонов
Обозначение диапазона
Частоты
VHF (очень высокие частоты, ОВЧ)
30 ÷ 300 МГц
UHF (ультравысокие частоты, УВЧ) 300 ÷ 1000 МГц
P (иногда включается в L–диапазон) 230 ÷ 1000 МГц
L
1 ÷ 2 ГГц
S
2 ÷ 4 ГГц
C
4 ÷ 8 ГГц
X
8 ÷ 12.5 ГГц
Ku
12.5 ÷ 18 ГГц
K
18 ÷ 26.5 ГГц
Ka
26.5 ÷ 40 ГГц
Миллимитровые волны
свыше 40 ГГц
свойствами, характеризующими способность среды запасать энергию волн.
То же самое относится к волнам иной физической природы, например, звуковым волнам, волнам в направляющих структурах и т. д., включая процесс
распространения электромагнитных волн.
Инерция среды при распространении электромагнитных волн связана
с индуктивными свойствами среды и характеризуется магнитной проницаемостью. Упругость среды соответствует ее электрической емкости, характеризуется диэлектрической проницаемостью. Иными словами, накопление
магнитной энергии обусловлено магнитной проницаемостью µ, а накопление
потенциальной энергии, или энергии электрического поля, обусловлено диэлектрической проницаемостью ε. Если материал — диэлектрик, то процесс
распространения радиоволн определяется только величинами ε и µ. Поэтому чисто волновое уравнение будет справедливо как для вектора магнитного
~ так и для вектора электрического поля E.
~ Если среда — проводник,
поля H,
и характеризуется ε, µ и проводимостью σ, то происходит поглощение энергии волн. В этом разделе мы рассмотрим распространение электромагнитных
волн в средах с удельной проводимостью, равной нулю. К таким средам относятся чистые диэлектрики.
60.
603.1
3.1.1
Волновое уравнение для электромагнитных волн
Уравнения Максвелла
В основе теории излучающих систем лежат уравнения Максвелла.
Первое уравнение Максвелла
Теорема Гаусса утверждает, что
ΦE = 4πQ.
Здесь ΦE — поток через замкнутую поверхность, границу объема V ; Q —
сумма зарядов в объеме V .
Теорема доказывается для неподвижных зарядов. По предположению
Максвелла, формулировка теоремы остается справедливой и для движущихся зарядов. Все следствия из этого предположения согласуются с опытом,
следовательно, так оно и есть.
Факультативно. Физический смысл дивергенции: дивергенция — объемная плотность потока. Другими словами: дивергенция — производная во все
стороны.
Запишем электростатическую теорему Гауса в дифференциальной форме.
ΦE
4πQ
1
=
.
ΦE = 4πQ | · ⇒
V
V
V
V →0
Отсюда:
~ = 4πρ,
div E
(3.1)
здесь ρ — объёмная плотность заряда.
Из курса общей физики по электричеству хорошо известно, что в случае,
когда мы имеем дело не с вакуумом (свободным пространством), а с реальной
средой, то уравнение (3.1) запишется в виде:
~ = 4πρ.
div D
(3.2)
Второе уравнение Максвелла
Закон электромагнитной индукции Фарадея гласит, что при изменении по~ через контур в контуре возникает э.д.с. индуктока ΦB магнитного поля B
61.
61ции Eind
1 dΦB
Eind = − ·
.
(3.3)
c dt
Э.д.с. возникает, и если поток ΦB изменяется при перемещении или деформации контура, и если контур неподвижен, а поток ΦB изменяется за счет
~
изменения магнитного поля B.
Однако закон Фарадея можно доказать только для случая, когда поле
~ не изменяется во времени.
B
Максвелл предположил, что изменение магнитного поля вызывает появление вихревого электрического поля, и это поле приводит к появлению Eind
~
1 ∂B
~
.
rot E = − ·
c ∂t
(3.4)
В выражении (3.4) полная производная по времени заменена частной,
чтобы подчеркнуть неподвижность контура, неизменность его пространственных координат.
~ = 0. Для переменных
Необходимо сказать, что в электростатике rot(E)
~ 6= 0 и поле E
~ — вихревое, не потенциальное.
полей rot(E)
Третье уравнения Максвелла
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю, иными словами:
ΦB = 0,
или в дифференциальной форме:
~ = 0,
div B
(3.5)
что означает отсутствие магнитных зарядов, т. е. линии магнитного поля замкнуты (не рвуться).
Четвертое уравнение Максвелла
Хорошо известное из магнитостатики уравнение
4π
~ = ~j
rot H
c
(3.6)
62.
62противоречит уравнению непрерывности
∂ρ
div ~j +
= 0,
∂t
т. е., в общем случае изменение заряда в системе, в которой присутствует
электрический ток, не будет равным нулю:
∂ρ
∂t
6= 0.
Действительно, с одной стороны:
h
i h
i
~
~
~
~
~
~
~
div rot H
= ∇, ∇, H = H, ∇, ∇ = 0.
С другой стороны, при
∂ρ
∂t
6= 0:
~
div rot H
= div
4π
~j
c
!
4π 4π
= div ~j =
·
c
c
−
∂ρ
∂t
!
6= 0.
∂ρ
6= 0, можно предположить,
Чтобы обобщить уравнение (3.6) на случай
∂t
что
4π
~
~ = ~j + X,
(3.7)
rot H
c
~ — необходимая поправка к уравнению магнитостатики.
где X
Действительно:
~
0 = div rot H
= div
4π
~
~j + X
c
!
=
4π
c
~ .
~
div j + div X
Учтем, что
∂ρ
div ~j = − ,
∂t
и получим
4π ∂ρ
~ .
0=− ·
+ div X
c ∂t
63.
63Учтем теперь, что
~ ,
4πρ = div D
и получим
!
~
~
1 ∂D
1 ∂ div D
~ − ·
~ = div X
0=− ·
+ div X
= 0.
c
∂t
c ∂t
Таким образом, мы получили:
~
1 ∂D
~ − ·
div X
c ∂t
!
= 0.
(3.8)
Из того, что дивергенция некоторого поля
равна нулю, вовсе не следует,
~ = 0 не означает, что B
~ = 0.
что само поле равно нулю. Например, div B
Максвелл сделал предположение, что в уравнении (3.8)
~ −
X
~
1 ∂D
·
= 0.
c ∂t
В этом случае необходимую поправку к уравнению магнитостатики (3.7) можно записать в виде
~
1 ∂D
~
X= ·
.
c ∂t
Размерность величины
~
∂D
∂t
=
∂
∂t
~
εE =
заряд
время × площадь
совпадает с размерностью тока, приходящегося на единицу площади.
Таким образом, Максвелл получил:
4π
~
1 ∂D
~
~
rot H = j + ·
.
c
c ∂t
(3.9)
Максвелл ввел понятие токов смещения:
~
~jd ≡ 1 · ∂ D .
4π ∂t
(3.10)
64.
64Данный ток получил такое название потому, что он выражается через вектор
~
электрического смещения D.
Тогда
4π
~
~
~
rot H =
j + jd .
(3.11)
c
Таким образом, можем записать, что
4π
~ =
~j + ~jd ,
rot H
c
div rot H
~
= 0.
Отсюда следует, что
~
~
div j + jd = 0 ⇒ Φ~j+~jd = 0.
(3.12)
Таким образом мы получили, что плотность потока вектора суммарного
тока (~j + ~jd ) через любую замкнутую поверхность равна нулю, т. е. линии
суммы токов проводимости и токов смещения замкнуты (не рвутся).
Из уравнения (3.12) Максвеллом был сделан очень важный вывод о возможности излучения и распространения электромагнитных волн в диэлектрике и свободном пространстве (вакууме). Справедливость этого вывода
была доказана экспериментально немецким физиком Генрихом Герцем.
Окончательно, запишем уравнения Максвелла в дифференциальной форме. Теория электромагнитного поля сводится к четырем соотношениям2 , образующим систему уравнений Максвелла (3.13), два из которых являются
стационарными, а два других зависят от времени (динамические уравнения).
Динамические уравнения устанавливают связь между изменениями во времени магнитной индукции с пространственными изменениями электрического
поля и наоборот, между изменениями во времени электрического поля с про2
Здесь все уравнения записаны в системе СИ
65.
65странственными изменениями магнитного поля.
~ = ρ;
div D
~
∂B
~
rot E = − ;
∂t
~
div B = 0;
~
∂D
rot H
~ = ~j +
.
∂t
(3.13)
Чтобы уравнения имело смысл решать относительно электрического и
магнитного полей, нужно дополнить их так называемыми материальными
уравнениями:
~
~
D = εE, ε = ε0 εr ;
~ = µH,
~
(3.14)
B
µ = µ0 µr ;
~
~
j = σ E.
Кроме того, заряды и токи связаны уравнением непрерывности:
∂ρ
div ~j +
= 0.
∂t
(3.15)
Таким образом, полная система уравнений Максвелла — это 8 одномер~ (Ex ,
ных уравнений для 6 одномерных неизвестных — проекций векторов E
~ (Hx , Hy , Hz ). В системе дифференциальных уравнений для
Ey , Ez ) и H
нескольких функций одной и той же переменной, как и для системы обычных
алгебраических уравнений, нужно, чтобы число уравнений совпадало с числом неизвестных. Произвол, который содержится в решении дифференциальных уравнений с одной переменной — это несколько произвольных констант
интегрирования в решении уравнений. Если уравнения содержат функции
нескольких переменных и это уравнения в частных производных, то произвол решений гораздо больше. Для устранения этого произвола и необходимы
дополнительные дифференциальные уравнения.
3.1.2
Вывод волнового уравнения для среды без потерь
Инерция среды при распространении электромагнитных волн связана с
индуктивными свойствами среды и характеризуется магнитной проницаемо-
66.
66стью (µ). Упругость среды соответствует её электрической емкости, которая
характеризуется диэлектрической проницаемостью ε.
Иными словами, накопление магнитной энергии обусловлено магнитной проницаемостью среды распространения (µ), а накопление потенциальной энергии, или энергии электрического поля, обусловлено диэлектрической
проницаемостью среды (ε). Так как мы приняли, что среда распространения
не имеет потерь, то проводимость среды σ будет равна нулю.
Ранее было показано, что при анализе распространения электромагнитных волн необходимо учитывать два вида тока:
~
1. ток проводимости, подчиняющийся Закону Ома: J~ = σ E;
~
∂D
.
2. ток смещения с плотностью
∂t
В среде с конечными µ и ε, но σ = 0, ток смещения будет единствен~ иH
~ определяются чисто волновым уравнением.
ном током. В этом случае E
Затухания волн не будет.
При σ 6= 0 появляется ток проводимости, приводящий к потерям. Амплитуда волны будет уменьшаться с расстоянием. Относительная величина
этих токов зависит от частоты поля.
Рассмотрим плоские волны, т. е. волны, у которых поверхности равных
фаз являются плоскостями. Будем считать, что свойства волн не изменяются
в плоскости XY . Если свойства среды не зависят от X и Y , то ∂/∂x = 0,
∂/∂y = 0.
Запишем уравнения Максвелла, зависящие от времени.
h
i
~
~
∂B
∂H
~
~
~
rot(E) = ∇, E = −
= −µ
:
∂t
∂t
−µ
−µ
−µ
∂Hx
∂t
∂Hy
∂t
∂Hz
∂t
=
=
=
∂Ez
∂y
∂Ex
∂z
∂Ey
∂x
−
−
−
∂Ey
∂z
∂Ez
∂x
∂Ex
∂y
;
;
.
h
i ∂D
~
~
∂E
~
~
~
rot(H) = ∇, H =
=ε
:
∂t
∂t
ε
(3.16)
ε
ε
∂Ex
∂t
∂Ey
∂t
∂Ez
∂t
=
=
=
∂Hz
∂y
∂Hx
∂z
∂Hy
∂x
−
−
−
∂Hy
∂z
∂Hz
∂x
∂Hx
∂y
;
;
(3.17)
.
Распишем стационарные уравнения Максвелла. Предположим, что среда
однородна и величины µ и ε не зависят от координат. Тогда первое стацио-
67.
67нарное уравнение (3.1) запишется в виде:
∂Ex
~ = ∇,
~ D
~ =ε
div(D)
∂x
∂Ey
+
∂y
+
∂Ez
!
= ρ,
∂z
где ρ — объемная плотность заряда.
Уравнение означает, что изменение электрической индукции в малом
элементе объема dV = dx · dy · dz с плотностью зарядов ρ зависит от величины ∂ρ/∂t.
Если внутри малого объема dV зарядов нет (т. е. ρ = 0), то первое стационарное уравнение перепишется в виде:
ε
∂Ex
∂x
+
∂Ey
∂y
+
∂Ez
!
(3.18)
= 0.
∂z
Уравнение (3.18) означает, что число линий потока электрической индукции, входящих в элемент объема dV , равно числу линий потока, выходящих
из этого объема.
Второе стационарное уравнение записывается так:
~ = ∇,
~ B
~ =µ
div(B)
∂Hx
∂x
+
∂Hy
∂y
+
∂Hz
!
∂z
= 0.
(3.19)
Согласно второму стационарному уравнению Максвелла, число линий
потока магнитной индукции, входящих и выходящих из элемента объёма dV ,
должны быть равны между собой.
Волновое уравнение для электромагнитных волн
Для плоских волн в выбранной нами системе координат все производные
по x и y равны нулю. Поэтому из уравнений (3.16) и (3.19) для напряженности
магнитного поля можем записать:
−µ
∂Hz
∂t
= 0;
∂Hz
∂z
= 0.
Это возможно, если Hz постоянна в пространстве и времени. Она не
может влиять на волновое движение, поэтому можно считать Hz = 0.
68.
68Аналогично из уравнений (3.17) и (3.18) для напряженности электрического поля придем к Ez = 0.
Постоянство значений Hz и Ez означает, что колебания (изменения) происходят в направлениях, ортогональных оси Z.
Упростим задачу. Будем рассматривать плоскополяризованные волны.
Положим, что колебания электрического поля осуществляются вдоль оси X,
т. е. будем рассматривать поле Ex , полагая Ey = 0.
В этом случае из уравнений Максвелла (3.16) и (3.17), зависящих от
времени следует, что:
−µ
∂Hy
∂t
=
∂Ex
∂z
;
(3.20)
ε
∂Ex
∂t
=
∂Hy
∂z
.
(3.21)
Учитывая соотношения
∂2
∂2
=
∂z · ∂t ∂t · ∂z
и взяв производные от уравнения (3.20) по t и уравнения (3.21) по z, найдем
волновое уравнение для Hy .
−µ
∂ 2 Hy
∂t2
=
∂ 2 Ex
∂z · ∂t
,
2
∂ 2 Ex = − ∂ Hy .
ε
∂z 2
∂t · ∂z
Отсюда получаем, что
∂ 2 Hy
∂ 2 Hy
= µε 2 .
(3.22)
∂z 2
∂t
Аналогично, дифференцируя (3.21) по t, а (3.20) по z, получим волновое
уравнение для Ex :
∂ 2 Ex
∂ 2 Ex
= µε 2 .
(3.23)
∂z 2
∂t
Таким образом, оба поля, Ex и Hy , подчиняются одному и тому же волновому уравнению, распространяясь вдоль оси Z с одинаковой скоростью:
v2 =
1
µε
(3.24)
69.
69В свободном пространстве скорость распространения волны v равна скорости света c (v = c):
1
c2 =
.
µ0 ε0
Здесь µ0 — магнитная постоянная, физическая константа, определяющая
плотность магнитного потока в вакууме; ε0 — электрическая постоянная,
определяющая диэлектрическую проницаемость свободного пространства (вакуума).
Известно, что в системе СИ µ0 = 1.26·10−6 Гн/м [(В·с)/(А·м)], ε0 = 8.85·
10−12 Ф/м [(А·с)/(В·м)], тогда получаем значение скорости распространения
электромагнитной волны в свободном пространстве (скорости света):
c= √
1
µ0 ε0
= 2.998 · 108
м
с
.
Для плоских волн, т. е. волн, у которых поверхности равных фаз представляют собой плоскости, решение волновых уравнений могут быть записаны в виде:
Ex = E0 sin
2π
λ
!
(vt − z) ,
Hy = H0 sin
2π
λ
!
(vt − z) ,
(3.25)
где E0 , H0 — амплитуды полей E и H; λ — длина волны; v — фазовая скорость
волны.
То, что решение получено в виде sin (cos), связано с отсутствием поглощения (σ = 0).
Векторное произведение
h
i
~
~
~
Π = E, H
(3.26)
называется вектором Пойнтинга, или вектором Умова–Пойнтинга.
Электромагнитная волна является поперечной волной, т.к. Ez и Hz постоянны и равныh нулю.i Направление её распространения совпадает с направ~ H
~ = Π.
~
лением вектора E,
~ = Ex · Hy и направлен вдоль оси Z.
В рассмотренном случае Π
70.
70Рисунок 3.1 — Электромагнитная волна (Ex ,Hy ), распространяющаяся вдоль
оси Z. Векторы электрического поля Ex и магнитного поля Hy таковы, что
электрическая и магнитная составляющие взаимно перпендикулярны. Если
среда не проводящая (т. е. σ = 0), то электрическая и магнитная составляющие электромагнитной волны находятся в фазе
Это векторное произведение имеет размерность:
напряжение × ток
длина × длина
электрическая мощность
.
площадь
=
h
i
~ H
~ определяет плотность потока энерТаким образом, вектор Пойнтинга E,
гии.
Подставим решения (3.25) в уравнение (3.20), получим соотношение:
µv · Hy = Ex .
Учтем, что
v2 =
1
µε
и преобразуем эти соотношения к виду
√
µHy =
Отсюда следует
√
εEx .
s
Z=
Ex
Hy
=
µ
ε
[Ом] .
(3.27)
71.
71Данная величина имеет размерность сопротивления и называется волновым сопротивлением (импедансом) среды распространения.
Для свободного пространства
s
Z0 =
3.1.3
µ0
ε0
= 376.7 Ом.
Электромагнитные волны в средах с потерями
В природе не существует чистых диэлектриков, и любая реальная среда
(вещество) обладает некоторой проводимостью. Электромагнитные волны в
таких средах затухают. Ниже мы получим волновое уравнение для сред с
проводимостью σ 6= 0.
Для определенности будем рассматривать поведение электрического поля волны, считая, что магнитная составляющая ведёт себя аналогично. Запишем волновое уравнение для сред с нулевой проводимостью:
∂ 2 Ex
∂z 2
− µε
∂ 2 Ex
∂t2
(3.28)
= 0.
~ = εE,
~ где D
~ —
Материальное уравнение среды мы приняли в форме D
~ следующим образом:
вектор электрической индукции. Можно представить D
~ =E
~ + 4π P~ ,
D
где P~ — вектор поляризации среды. Если среда изотропна, то вектор P~ кол~ В слабых полях вектор P~ связан с E
~ зависимостью:
линеарен вектору E.
~
P~ = χE.
Перепишем уравнение (3.28) в виде:
2
"
∂ Ex
∂
∂z
∂t ∂t
−µ
2
∂
#
(εEx ) =
2
∂ Ex
∂z
−µ
2
"
#
∂ ∂Dx
= 0.
∂t ∂t
72.
72∂Dx
Здесь учитывается только ток смещения
!
∂t
. Если σ 6= 0, необходимо
~
учитывать ещё и ток проводимости, плотность которого равна ~j = σ E.
Тогда уравнение Максвелла, связывающее пространственные изменения
магнитного поля с временными изменениями электрического поля, примет
вид:
∂D
~
~ =
+ ~j.
(3.29)
rot H
∂t
~ на ось x:
Будем рассматривать проекцию поля E
−
∂Hy
∂z
=ε
∂Ex
∂t
(3.30)
+ σEx .
Из уравнения Максвелла (3.16), связывающего пространственные изменения
~ с временными изменениями H,
~ следует:
E
−µ
∂Hy
∂t
=
∂Ex
∂z
(3.31)
.
Продифференцируем уравнение (3.30) по t, а уравнение (3.31) по z:
ε
∂ 2 Ex
∂t2
+σ
∂Ex
∂t
=−
∂ 2 Hy
∂z∂t
;
1 ∂ 2 Ex
∂ 2 Hy
=−
.
µ ∂z 2
∂z∂t
Так как правые части обоих уравнений одинаковы, можем записать:
1 ∂ 2 Ex
∂ 2 Ex
∂Ex
µ ∂z
∂t
∂t
=ε
2
+σ
2
и окончательно получим:
∂ 2 Ex
∂ 2 Ex
∂Ex
∂z
∂t
∂t
= µε
2
+ µσ
2
.
(3.32)
Таким образом, учет проводимости среды привел
к добавлению в волно!
∂Ex
, приводящего к затуханию
вое уравнение диффузионного члена µσ
∂t
волн.
73.
73Произведение (µσ)−1 имеет размерность [м−2 с−1 ] и называется магнитным коэффициентом диффузии.
Пусть зависимость Ex имеет гармонический характер:
Ex = E0 eiωt .
Подставим Ex в уравнение (3.32):
∂ 2 Ex
∂z
2
−
iωµσ
−
ω
µε
Ex = 0
2
и перепишем его в виде
∂ 2 Ex
∂z 2
− γ 2 Ex = 0,
(3.33)
где γ 2 = iωµσ − ω 2 µε.
Таким образом мы свели волновое уравнение к уравнению Гельмгольца.
Это уравнение имеет решения, содержащие члены типа e−γz и eγz . Будем
рассматривать волну Ex , бегущую в положительном направлении оси z, т. е.
рассматривать решения типа
Ex = E0 eiωt e−γz .
(3.34)
Это уравнение описывает волну в среде с потерями, бегущую в положительном направлении оси Z. Электромагнитная волна, распространяясь
в среде с конечной проводимостью, не остается постоянной по амплитуде, а
убывает по экспоненциальному закону. Это вызвано тем, что в такой среде
электромагнитная энергия рассеивается (в конечном итоге в тепло).
Оценим относительное значение членов, входящих в правую часть уравнения (3.32), для различных сред.
Электромагнитные волны в диэлектриках
В диэлектриках преобладают токи смещения, поэтому выполняется соотношение:
J~
~
∂D
∂t
, или σ ωε.
74.
74∂Ex
Тогда диффузионным членом µσ
в уравнении (3.32) можно прене∂t
бречь.
∂ 2 Ex
При учёте только члена µε 2 выражение для γ 2 можем записать в
∂t
виде
√
γ 2 = −ω 2 µε ⇒ γ = iω µε.
Запишем выражение для поля в следующем виде:
√
Ex = E0 eiωt e−γ·z = E0 ei(ω·t−ω εµ·z )
Учтем, что
1
v=√
µε
и
k=
ω
c
.
Окончательно получим
Ex = E0 ei(ω·t−k·z)
(3.35)
уравнение плоской волны, распространяющейся без затухания в направлении
положительных значений оси Z.
Электромагнитные волны в проводниках
В проводниках преобладают токи проводимости
~
∂D
~
J
, или σ ωε
∂t
В этом случае в уравнении (3.32) можно пренебречь членом µε
тогда выражение для γ 2 запишется в виде:
γ 2 = iσωµ.
Учтем, что
√
1+i
i = √ , и получим:
2
r
ωµσ
.
γ = (1 + i)
2
∂ 2 Ex
∂t2
,
75.
75Запишем выражение для поля:
Ex = E0 eiωt e−γ·z = E0 e
1
ωµσ 2
i ωt−( 2 ) ·z
−( ωµσ
2 ) ·z
1
2
e
(3.36)
Таким образом,h амплитуда волны
в процессе распространения уменьшаi
1
ется по закону exp (−ωµσ/2) 2 · z . Т. е. в проводнике поле экспоненциально
затухает и уменьшается в e раз на расстоянии
s
δ=
2
ωµσ
.
(3.37)
Здесь δ определяет толщину скин–слоя.
Выражение (3.37), в частности, объясняет возможность осуществления
радиосвязи с субмаринами, находящимися в подводном
h
i положении.
Электрическая проводимость воды σ = 3 Сименс
метр ; магнитная проницаh
i
емость воды µ = 1.257 · 10−6 Генри
метр . Выберем самую нижнюю частоту из
радиочастотного диапазона f = 3 · 103 Гц.
s
2
δ=
≈ 5.3 м.
2πf · µ · σ
Таким образом, для осуществления сеанса связи с командным пунктом
подводной лодке необходимо подвсплыть на глубину, обеспечивающую нахождение приёмной антенны на расстоянии ∼ 3 ÷ 4 м от поверхности воды.
Наличие в проводниках свободных электронов приводит к появлению
~ Именэлектрического тока при приложении внешнего электрического поля E.
но поэтому, в частности, в приёмных антеннах возникает электрический ток,
который по фидерному тракту поступает в радиоприемное устройство.
Известно, что у воздуха относительная магнитная проницаемость µr =
1.00000037 ≈ 1, а относительная диэлектрическая проницаемость εr = 1.000594
≈ 1. Таким образом, волновое сопротивление воздуха составляет:
s
µr µ0
≈ 377 Ом.
ZВ =
εr ε0
76.
763.2
Критерий разделения сред на диэлектрики и проводники
~ постоянно, то поле внутри проводника равно нулю, т. к. внешЕсли E
нее поле скомпенсировано полем, образованным зарядами, которые под его
воздействием сместились к поверхности проводника.
~ то потребуется некоторе
Если резко изменить напряжённость поля E,
время τ для того, что бы электроны сместились и было создано внутренне
поле, компенсирующее внешнее. Время τ −1 определяет граничную частоту
ωгр . Волны с частотой, больше граничной, успевают больше проникнуть в
проводник, т. к. при ω > τ −1 электроны не успевают занять положение, при
котором достигается компенсация внешнего поля, и волны с частотой ω > ωгр
будут распространяться в проводнике.
На очень высоких частотах электроны вообще не будут успевать реагировать на внешнее поле, и среда становится прозрачной для этих частот.
Отношение плотности тока проводимости к плотности тока смещения
равно
J~
~
∂D
=
σ
εω
.
(3.38)
∂t
По отношению этих токов и определяется, к какому классу веществ следует относить среду при распространении электромагнитных волн. Важны
не только значения ε и σ, но и частоты ω. На разных частотах одно и то же
вещество может проявлять различные свойства. Поясним это.
Рисунок 3.2 — Критерий разделения сред на диэлектрики и проводники
77.
77Среду можно представить в виде простой схемы, состоящей из конденсатора и сопротивления, соединенных параллельно, между которыми распределен полный ток в среде, как это показано на рисунке 3.2.
Если проводимость σ велика, то большая часть тока проходит через со1
противление; если реактанс ωε
мал, то основная часть тока проходит по емкостной цепи в виде тока смещения. Поэтому при σ ωε среду относим к
проводникам, при σ ≈ ωε — к полупроводящим средам, а при σ ωε — к
диэлектрикам.
Частота, при которой токи проводимости и смещения равны, называется
граничной частотой:
σ
(3.39)
ωгр = .
ε
На высоких частотах ω ωгр из-за преобладания токов смещения среда
проявляет свойства диэлектрика для распространяющейся электромагнитной
волны. На низких частотах ω ωгр в среде преобладают токи проводимости,
и ее можно рассматривать как проводник.
i
h
сименс
7
Для примера рассмотрим медь. Её проводимость σ = 5.8 × 10
метр .
h
i
Диэлектрическая проницаемость ε = 9 × 10−12 фарада
метр . Тогда отношение
σ
εω
≈
1018
частота
.
На частотах до области ультрафиолета (f 6 1016 Гц)
σ
εω
> 100,
т. е. медь является полупроводником. На частоте f = 1020 Гц (рентгеновское
излучение)
σ
< 100
εω
и медь является диэлектриком. Это, в частности, объясняет тот факт, что
медный лист является прозрачным для рентгеновских лучей.
Для иллюстрации в таблице 3.3 приведены граничные частоты для различных сред, представляющих интерес при распространении радиоволн в атмосфере Земли.
78.
78Таблица 3.3 — Граничные частоты для различных сред
№
Среда
Граничная частота
Диапазон волн
3
1.
Сухая почва
∼ 3 × 10 Гц
Средние волны
7
2. Влажная почва
∼ 10 Гц
Короткие волны
5
3. Пресная вода
∼ 2 × 10 Гц
Короткие волны
9
4. Морская вода
∼ 3 × 10 Гц
Сантиметровые волны
3.3
Среда — полупроводник
В предыдущем разделе было показано, что в природе не существует чистых (абсолютных) диэлектриков или проводников. Всё определяется соотношением (3.38). Таким образом, при распространении электромагнитных волн
в реальной среде необходимо учитывать её проводимость.
Удобно рассматривать распространение электромагнитных волн в полупроводящей среде, используя понятие комплексной диэлектрической проницаемости:
σ
ε0 = ε − i .
(3.40)
ω
Это величина, учитывающая потери в среде, обусловленные наличием
проводимости. Ее использование позволяет в средах с потерями пользоваться
теми же зависимостями (по форме записи), что и для диэлектриков.
Рассмотрим уравнение Максвелла:
~
~
∂E
∂H
~
~
~
.
rot H = σ E + ε ; rot E = −µ
∂t
∂t
(3.41)
Предполагаем, что поля изменяются по гармоническому закону:
~ =E
~ 0 eiωt ;
E
~ =H
~ 0 eiωt .
H
~ иH
~ в уравнение Максвелла:
Подставим E
!
σ
~ = (σ + iωε)E
~ = iω ε − i
~ = iωε0 E,
~
rot H
E
ω
~ = −iωµH.
~
rot E
(3.42)
79.
79Таким образом, мы получили уравнения, позволяющие рассматривать
полупроводник как диэлектрик с комплексной диэлектрической постоянной.
Это позволяет пользоваться результатами, полученными на предыдущих лекциях, заменив вещественную диэлектрическую постоянную ε на комплексную ε0 .
Введем комплексное значение фазового множителя k 0 и представим его
в виде:
k 0 = k − iα,
(3.43)
где k и α — вещественные числа. Комплексный фазовый множитель полностью характеризует движение волны. Вещественная часть имеет тот же
смысл, что и волновой параметр k в диэлектриках, т. е. определяет фазовую
скорость. Член α определяет пространственное затухание волны. Выражение
~ принимает вид:
для E
~ =E
~ 0 e−ik0 z eiω·t E
~ 0 e−i(k−iα)z eiω·t E
~ 0 e−ikz e−α·z eiω·t E
~ 0 e−α·z ei(ω·t−k·z) .
E
Комплексный характер фазового множителя означает, что волна, распространяясь вдоль оси z, затухает. Причиной затухания является поглощение
энергии из-за наличия проводимости.
Введем комплексное волновое сопротивление Z 0 . Z — модуль комплексного волнового сопротивления; ϕ — его аргумент.
В таблице 3.4 записаны основные соотношения, определяющие параметры распространения электромагнитной волны в среде, имеющей комплексный характер диэлектрической проницаемости. Для сравнения в левой колонке таблицы 3.4 приведены те же соотношения для среды, представлющей
собой диэлектрик.
Таким образом, для того чтобы определить характер распространения
гармонической волны в среде, имеющей некоторую проводимость, нам необходимо найти следующие параметры:
- α — коэффициент затухания;
- k — фазовый множитель;
- Z и ϕ модуль и аргумент комплексного волнового сопротивления;
- vф — фазовую скорость для полупроводящей среды.
80.
80Таблица 3.4 — Основные соотношения для гармонической волны, бегущей в
положительном направлении оси z
Волна в диэлектрике
Волна в полупроводнике
~ =E
~ 0 e−ikz eiωt
~ =E
~ 0 e−ik0 z eiωt
E
E
~0
~0
E
E
0
−ikz iωt
~
~
H= e
e
H = 0 e−ik z eiωt
Z
Z
√
ω
ω
√
k = = ω εµ
k 0 = 0 = ω ε0 µ
v
v
— волновое
число
—
комплексное
волновое число
r
r
µ
µ
Z=
— волновое
Z0 =
— комплексное
ε
ε0
сопротивление
волновое сопротивление
Выражение для комплексного волнового числа (3.43) с учетом определения, данного для фазовой скорости (2.2), можно записать в виде:
k 0 = k − iα =
ω
v0
.
(3.44)
С учетом выражения для комплексной диэлектрической проницаемости (3.40),
а также выражения для комплексного волнового числа, приведенного в таблице 3.4, соотношение (3.44) можно переписать в виде:
v
!
u
u
p
σ
k 0 = ω ε0 µ = ω t ε − i
µ.
ω
С другой стороны:
v
! 2
u
σ
ω 2 σµ
u
2
t
ε−i
µ = ω εµ − i
= ω 2 εµ − iσµω= γ 2 .
ω
ω
ω
Т. е. получили, что:
γ 2 = (k 0 )2 = (k − iα)2 = k 2 − i(2kα) − α2 .
(3.45)
81.
81Таким образом,
(3.46)
k 2 − i(2kα) − α2 = ω 2 εµ − iσµω.
Приравняем действительную и мнимую части в выражении (3.46):
k 2 − α2 = ω 2 εµ,
(3.47)
2kα = σµω.
Найдем модуль комплексного k 0 :
s
p
|k | = k 2 + α2 =
0
q
2
2
2
(ω 2 µε) + (σµω) = ω µ ε2 +
σ2
ω2
(3.48)
.
Используя (3.48) и (3.47), получим:
r
2k 2 = ω 2 εµ + ω 2 µ
ε2 +
σ2
ω2
"
r
= ω 2 εµ · 1 +
1+
σ 2
ωε
#
.
Аналогично можно получить выражение для α.
В итоге получим модуль и аргумент для комплексного волнового числа
(волнового параметра):
v
u
2
u
ω
εµ
2
· +1 + t1 +
k =
2
v
u
2
u
ω
εµ
2
α =
· −1 + t1 +
2
σ
!2
,
ωε
σ
!2
ωε
(3.49)
.
Из второго уравнения системы (3.46) следует, что
2kα = σµω
→
k=
σµω
.
2α
Результат подставим в выражение для фазовой скорости и получим:
vф =
ω
k
=
2α
µσ
.
(3.50)
82.
82Найдем модуль (Z) и аргумент (ϕ) комплексного волнового сопротивления полупроводящей среды Z 0 .
s
Z0 =
µ
µ
=
√ .
ε0
µε
Учтём, что
k0 = ω
p
ωµ
µε0 , тогда k 0 = 0 .
Z
Отсюда следует, что
Z0 =
ωµ
ωµ
k
k − iα
=
0
= Zeiϕ .
Модуль комплексного волнового сопротивления Z 0 равен:
Z=√
ωµ
ωµ
=
=r
q
k 2 + α2
2
ω 2 µ ε2 + ωσ 2
2
µ
2
ε2 + ωσ 2
! 41
.
(3.51)
Перепишем выражение (3.51) в виде:
s
Z=
v
v
u
u
u
µ u
1
1
u
·u
=
Z
диэлектрика u
!2
!2 .
4
4
ε u
u
u
t1 + σ
t1 + σ
ωε
ωε
(3.52)
Найдем аргумент (ϕ) комплексного волнового сопротивления Z 0 :
ϕ = arctg
v
v
u
u
u
u
u
t−1 + t1 +
!
α
= arctg v
v
u
k
u
u
u
u
t
+1 + t1 +
σ
!2
ωε
.
!2
σ
ωε
(3.53)
83.
83Таким образом, при помощи выражений (3.49), (3.50), (3.52) и (3.53) можно определить характер распространения гармонической волны в полупроводящей среде. Рассмотрим несколько частных случаев.
3.3.1
Частные случаи: среда — диэлектрик
Рассмотрим частный случай. Пусть среда представляет собой диэлектрик. В этом случае σ ωε.
Найдём модуль и аргумент комплексного волнового числа (k и α): для
этого воспользуемся выражениями (3.49).
Найдём k:
v
!2
u
u
σ
ω 2 εµ
2
· +1 + t1 +
k =
.
2
ωε
При условии, что σ ωε,
σ
→ 0,
ωε
(3.54)
тогда
√ i ω 2 εµ
ω 2 εµ h
k =
· +1 + 1 =
· [+1 + 1] = ω 2 εµ.
2
2
Следовательно,
√
k = ω · εµ.
2
Найдем α:
v
u
2
u
ω
εµ
2
α =
· −1 + t1 +
2
σ
!2
ωε
ω 2 εµ
· [−1 + 1] = 0.
=
2
Следовательно,
α = 0.
Теперь определим фазовую скорость волны, для это воспользуемся выражением (3.50).
ω
ω
1
vф = = √ = √
k ω εµ
εµ
84.
84При помощи соотношения (3.52) найдем модуль комплексного волнового
сопротивления среды.
s v
u
µu
1
u
Z=
!2 .
4
εu
u
t1 + σ
ωε
С учётом соотношения (3.54) можем записать:
r r
r
µ4 1
µ
Z=
=
.
ε 1
ε
Теперь, при помощи выражения (3.53), найдем аргумент комплексного
волнового сопротивления.
v
v
u
u
u
u
u
t−1 + t1 +
ϕ = arctg v
v
u
u
u
u
u
t+1 + t1 +
σ
!2
ωε
.
!2
σ
ωε
С учётом соотношения (3.54) можем записать:
ϕ = arctg
p
√ !
−1 + 1
p
= arctg
√
+1 + 1
0
√
2
!
= arctg (0) .
Таким образом,
ϕ = 0.
Окончательно, для среды, в которой выполняется неравенство σ εµ,
справедливы следующие основные соотношения:
k=ω·
√
1
εµ, vф = √ , Z =
εµ
r
µ
,
ε
поглощение в среде отсутствует (α = 0). То есть мы пришли к выражениям,
полученным ранее для диэлектриков (смотри левую колонку таблицы 3.4).
85.
853.3.2
Частные случаи: среда — проводник
Теперь рассмотрим случай, когда среда распространения представляет
собой проводник, т. е. σ ωε. В этом случае
σ
→ ∞.
ωε
(3.55)
Найдем действительную (k) и мнимую (α) части комплексного волнового
параметра (k 0 ).
Запишем первое уравнение из системы (3.49):
v
u
2
u
ω
εµ
2
· +1 + t1 +
k =
2
σ
!2
ωε
.
Вообще говоря, если мы к бесконечности в квадрате прибавим единицу, то
получим бесконечность в квадрате, поэтому, с учетом соотношения (3.55)
предыдущее выражение можем переписать в виде:
ω 2 εµ h
σ i ω 2 µε ω 2 µεσ
ω 2 µε ωµσ
k ≈
· +1 +
=
+
=
+
.
2
ωε
2
2ωε
2
2
2
В силу того, что σ ωε, первое слагаемое в этом выражении можно будет
не учитывать, т. к. оно будет давать очень маленький вклад по сравнению со
вторым слагаемым. Таким образом мы получаем:
ω 2 εµ + ωµσ
ωµσ
k =
≈
.
2
2
2
Аналогичные рассуждения по отношению к α (смотри второе уравнение
системы (3.49)) позволят нам записать:
ωµσ
−ω 2 εµ + ωµσ
≈
.
α =
2
2
2
Таким образом, для проводника получили:
s
k=
s
ωµσ
2
, α=
ωµσ
2
.
(3.56)
86.
86Найдём выражение для фазовой скорости:
vф =
√
ω
ω 2
=√
=
k
ωεµ
s
2ω
µσ
.
(3.57)
Найдем модуль Z комплексного волнового сопротивления Z 0 . Запишем
выражение (3.52) для модуля импеданса и сделаем несколько простых математических преобразований:
v
v
s
u !2
u
u
2
µ u
1
1
(ωε)2
u µ
4 µ
u
u
·
Z=
!2 = u
!2 = ε2 · (ωε)2 + σ 2 =
4
4
ε u
ε
u
u
σ
t1 + σ
t
1+
ωε
ωε
s
s
2 2 2
µεω
µ2 ω 2
4
4
=
=
.
ε2 (ω 2 ε2 + σ 2 )
ω 2 ε2 + σ 2
s
Учитывая то, что среда является проводником, т. е. σ ωε, первым
слагаемым в знаменателе этого выражения можно пренебречь и переписать
его следующим образом:
s
4
Z≈
2 2
s
µω
µω
σ
σ
=
2
.
Найдем аргумент ϕ комплексного волнового сопротивления Z 0 .
s
ϕ = arctg
α
!
k
ωµσ
2
= arctg s
= arctg (1) .
ωµσ
2
Соответственно получаем, что
π
ϕ= .
4
(3.58)
87.
87Запишем комплексное волновое сопротивление для проводника в виде:
s
Z0 =
Ex
Hy
=
µω
σ
· exp i
π
4
!
.
(3.59)
π
Таким образом, согласно (3.59), в проводниках Hy отстает от Ex на по
4
фазе, что иллюстрируется на рисунке 3.3.
Рисунок 3.3 — Распространение плоскополяризованной электромагнитной
волны в случае, когда σ ωε. Магнитная компонента Hy отстаёт от электрической Ex на 45°
В хорошо проводящих средах волновое число k и коэффициент затухания α равны друг другу. Из-за высокой проводимости затухание волн велико
и растет с увеличением частоты. Фазовая скорость vф мала, соответственно
vф
мала и длина волны λ =
. В проводящих средах мало и волновое сопроf
тивление.
Ранее для диэлектрика было получено, что плотность энергии электрического и магнитного поля равны между собой, т. е.
1
2
µHy2 =
1
2
εEx2
88.
88В проводниках модуль импеданса, согласно выражению (3.59), есть
s
Z=
Ex
µω
=
Hy
σ
.
(3.60)
Из (3.60) следует:
1
2
1
µHy2
=
µ σ
ε ωµ
=
σ
.
ωε
εEx2
2
Из-за высокой проводимости это отношение очень велико и равно отношению тока проводимости к току смещения. Поэтому энергия магнитного
поля значительно превышает энергию электрического поля.
Учитывая, что между напряженностью электрического и магнитного поπ
лей существует сдвиг фаз ϕ = , среднее значение вектора Умова–Пойтинга
4
за период волны равно:
~ =
Π
1
1
~ H.
~
EH cos(ϕ) = √ E
2
2 2
С учетом того, что
~ =Z ·H
~ =H
~
E
получаем:
~2
ωµ
,
σ
s
ωµ
.
(3.61)
2
2σ
В проводниках распространение электромагнитной волны уже нельзя
рассматривать как волновой процесс, т. к. происходит быстрое, на масштабе
длины волны, затухание поля. Фазовая скорость связана с показателем преc
ломления соотношением n =
. Т. к. согласно (3.56) vф очень мала, то в
vф
проводящей среде велико значение показателя преломления. Этим объясняется хорошая отражательная способность проводников на высоких частотах,
включая оптический диапазон длин волн, это, в частности, объясняет тот
факт, что все металлы блестят.
~ =
Π
H
r
89.
89Согласно (3.56) фазовая скорость в проводнике зависит от частоты, поэтому электрический проводник является дисперсионной средой. В провод∂vф
< 0, следовательно, они обладают аномальной дисперсией, в рениках
∂λ
зультате этого групповая скорость в них выше фазовой.
3.4
Принцип Гюйгенса и зоны Френеля
Определим область пространства, в которой распространяется основная
часть радиоволны, формирующая сигнал в точке приёма. Размер и конфигурация такой области определяются принципом Гюйгенса–Френеля, согласно которому каждая точка фронта распространяющейся волны, созданной
каким-то первичным источником A, сама является источником новой сферической волны (рисунок 3.4).
Рисунок 3.4 — Представление фронта распространяющейся волны как совокупности элементарных излучателей Гюйгенса
Полное поле в точке приема B может быть определено либо непосредственно как поле первичных источников, либо путем суммирования элементарных полей, создаваемых вторичными источниками, распределенными по
замкнутой поверхности, охватывающей первичные источники. В теории такой вторичный источник называется элементарным источником Гюйгенса, и
диаграмма направленности его излучения имеет форму кардиоиды (F (ϕ) =
0.5 (1 + cos(ϕ))). Рассмотрим построение, предложенное Френелем (рисунок 3.5).
Пусть в точку A помещён излучатель, а в точку B — приёмная антенна.
Источник создаёт сферическую волну, т. е. волну, поверхностью равных фаз
которой является сфера с центром в точке A. Построим конические поверхности с вершиной в точке B и осью AB такие, чтобы длины образующих
соответствующих конических поверхностей отличались между собой на ве-
90.
90Рисунок 3.5 — Зоны Френеля
личины, пропорциональные
m
λ
2
(m = 1, 2, . . . ).
Тогда должны выполняться следующие равенства:
BN1 − BN0 = BN2 − BN1 = . . . = BNn − BNn−1 =
λ
2
(3.62)
Пересечение конусов с фронтом волны образует на сферической поверхности семейство коаксиальных окружностей. Участки поверхности сферы, заключённые между смежными окружностями, называются зонами Френеля.
Первая, или главная, зона Френеля — часть сферы, ограниченная окружностью N1 , зоны высших порядков представляют собой кольцевые области. Из
(3.62) следует, что фазы радиоволн, излучаемых виртуальными источниками
смежных зон, отличаются в среднем на π.
Рисунок 3.6 — Векторы напряжённости поля от зон Френеля
91.
91Разобьём каждую зону Френеля на большое количество колец конечной
ширины и просуммируем векторы напряжённости поля в точке приёма от
каждого кольца, как это показано на рисунке 3.6. Пусть Ei — результирующая амплитуда напряжённости поля волны в точке приёма от i-ой зоны
Френеля. Векторы от соседних зон направлены в противоположные стороны,
т. к. их фазы отличаются на π. С ростом i амплитуда Ei будет убывать как за
счёт удаления вторичных источников от точки приёма, так и потому, что направление максимума их излучения всё более отклоняется от направления на
точку приёма. Результирующую амплитуду волн от вторичных источников
всех зон Френеля можно представить в виде знакопеременного сходящегося
ряда
E = E1 − E2 + E3 − E4 + E5 − . . . =
E1
E3
E3
E5
E1
+
− E2 +
+
− E4 +
+ ... .
=
2
2
2
2
2
(3.63)
Обычно расстояние между передающей и приёмной антеннами значительно превышает длину волны, т. е.
l1 + l2 λ.
(3.64)
Тогда амплитуды Ei от соседних зон мало отличаются друг от друга и
можно считать, что
Ei−1 + Ei+1
,
Ei ≈
2
т. е. выражения в скобках в (3.63) близки к нулю. Таким образом, в результате
взаимной компенсации сигналов от соседних зон высших порядков результирующая амплитуда поля от всех зон Френеля
E≈
E1
,
2
т. е. эквивалентна излучению половины первой зоны Френеля (реально полной компенсации соседних зон не происходит, поэтому более точно E21 < E <
E1 ). В первом приближении полагают, что поверхность первой зоны Френеля и есть область пространства, ответственная за создание сигнала в точке
приёма.
92.
92Рисунок 3.7 — К определению радиусов зон Френеля
Зоны Френеля могут быть построены на поверхности произвольной формы. Найдём радиус n-й зоны Френеля на плоскости S, перпендикулярной направлению распространения, в предположении, что распространяется плоская радиоволна. Согласно обозначениям рисунка 3.7,
λ
ANn + Nn B − (l1 + l2 ) = n .
2
(3.65)
Если выполняется условие l1 , l2 λ, то
q
R2
ANn = l12 + Rn2 ≈ l1 + n ,
2l1
q
Rn2
2
2
Nn B = l2 + Rn ≈ l2 +
.
2l2
(3.66)
Подставив выражения (3.66) в (3.65), нетрудно получить выражение для радиуса n-й зоны Френеля:
r
nλl1 l2
Rn =
.
(3.67)
l1 + l2
Зафиксируем на плоскости S, перпендикулярной трассе AB, точки образующей n-й зоны Френеля и будем перемещать S вдоль трассы (рисунок 3.8).
Из (3.65) следует, что в этом случае выполняется равенство
ANn + Nn B = (l1 + l2 ) + n
λ
= const.
2
(3.68)
Математически (3.68) есть уравнение эллипса, следовательно, границы
зон Френеля в пространстве представляют собой поверхности эллипсоидов
вращения с фокусами в точках A и B. Области пространства между двумя со-
93.
93Рисунок 3.8 — Построение границ пространственных зон Френеля
седними эллипсоидами называют пространственными зонами Френеля. МакAB
симума радиус сечения эллипсоида плоскостью S достигает при l1 = l2 =
:
2
s
2 √
nλ AB
n · λ · AB
Rn max =
=
.
(3.69)
AB
2
2
94.
94ТЕМА 4
Отражение и преломление электромагнитных волн
на плоской границе раздела двух сред
4.1
Основные соотношения
Предположим, что во всех точках пространства электрические векторы
падающей волны параллельны друг другу. Такие волны называют плоско–
параллельными. В радиофизике принято плоскостью поляризации называть
~ электромагнитной волплоскость, содержащую электрическую компоненту E
ны.
Рассмотрим два частных случая, показанных на рисунке 4.1:
1. Волна поляризована нормально плоскости падения. Такую волну будем
~ ⊥ ).
называть волной с горизонтальной поляризацией (E
2. Волна поляризована в плоскости падения. Такую волну будем называть
~ || ).
волной с вертикальной поляризацией (E
Рисунок 4.1 — К определению поляризации электромагнитной волны
Будем считать, что среды являются полубесконечными и однородными
и границей их раздела является плоскость. На рисунке 4.2 приведены поло~ электромагнитной волны при отражении
жения вектора магнитного поля H
и преломлении волны.
~ 0, H
~ R, H
~ T — магнитные компоненты падающей, отраНа рисунке 4.2 H
женной и преломленной волн; Θ0 , ΘR , Ψ — углы падения, отражения, пре-
95.
95~ при отражении и
Рисунок 4.2 — Ориентация вектора магнитного поля H
преломлении электромагнитной волны
ломления; ~n0 , ~nR , ~nT — единичные векторы в направлении распространения
падающей, отраженной и преломленной волн. Поля считаем плоскими с заданными постоянными распространения k1 и k2 . Это позволяет решить задачу, не обращаясь непосредственно к уравнениям Максвелла. При решении
задачи необходимо удовлетворить граничным условиям на поверхности раздела сред. Рассмотрим их.
4.1.1
Граничные условия
При решении задачи необходимо удовлетворить граничным условиям на
поверхности раздела сред:
1. равенство тангенциальных составляющих напряженности магнитного
поля → Hτ 1 = Hτ 2 ;
2. равенство нормальных составляющих магнитной индукции → µ1 Hn1 =
µ2 Hn2 ;
3. равенство тангенциальных составляющих напряженностей электрического поля → Eτ 1 = Eτ 2 ;
4. равенство, вытекающее из уравнения Максвелла div(ε0 E) = ρ при ρ =
0 → ε01 En1 = ε02 En2 .
Если проводимость равна нулю (σ = 0), это условие превращается в
равенство нормальных составляющих электрической индукции на границе
96.
96раздела сред
ε1 En1 = ε2 En2 .
Для дальнейшего анализа достаточно любой пары граничных условий
~ или E).
~
(для H
4.1.2
Принятые обозначения
Запишем выражения для импедансов среды 1 и среды 2:
v
u
u µ1
t
0
Z1 =
,
ε01
v
u
u µ2
t
0
Z2 =
,
ε02
(4.1)
здесь ε01 и ε02 — комплексные диэлектрические проницаемости среды 1 и среды
2 соответственно. Ориентация векторов в плоской волне показана на рисунке 4.3.
Рисунок 4.3 — Ориентация векторов в плоской волне, ~r — расстояние вдоль
направления распространения волны.
Введём понятие волнового вектора
~k = k~n.
Здесь ~n — единичный вектор, нормальный к плоскости границы раздела двух
√
√
сред; k1 = ω µ1 ε1 и k2 = ω µ2 ε2 — волновые числа для среды 1 и среды 2.
Таким образом, запишем выражения для векторов напряженностей электромагнитного поля.
Падающая волна:
h
i
~
~n0 E0
i[k1 (~n0~r)−ωt]
~
~
~
E1 = E0 e
, H1 =
ei[k1 (~n0~r)−ωt] .
ρ1
97.
97Отраженная волна:
~R = E
~ 1 ei[k2 (~nR~r)−ωt] ,
E
h
i
~
~nR E1
~
HR =
ei[k1 (~nR~r)−ωt] .
ρ1
Преломленная волна:
~T = E
~ 2 ei[k2 (~nT ~r)−ωt] ,
E
4.1.3
i
h
~
~nT E2
~T =
H
ei[k2 (~nT ~r)−ωt] .
ρ2
Отражение и преломление плоских волн
Для границы раздела двух сред из граничного условия 3 следует (смотри
подраздел 4.1.1):
~ 1τ + E
~ Rτ = E
~Tτ .
E
Следовательно,
~ 0τ eik1 (~n0~r) + E
~ 1τ eik1 (~nR~r) = E
~ 2τ eik2 (~nT ~r) .
E
Это условие выполняется для любой точки границы раздела сред, что
возможно при равенстве всех фазовых множителей
k1 (~n0~r) = k1 (~nR~r) = k2 (~nT ~r) .
Учтем, что на плоскости раздела сред ~n~r = 0.
Используем известные зависимости:
~r (~n~n) = ~r = ~n (~n~r) − [~n [~n~r]] = − [~n [~n~r]] .
Следовательно, мы можем записать:
k1~n0 [~n [~n~r]] = k1~nR [~n [~n~r]] = k2~nT [~n [~n~r]] .
Осуществим циклическую перестановку векторов:
k1 [~n0~n] [~n~r] = k1 [~nR~n] [~n~r] = k1 [~nT ~n] [~n~r] .
98.
98Отсюда получаем:
k1 [~n0~n] = k1 [~nR~n] = k2 [~nT ~n] .
(4.2)
Из равенства (4.2) следует:
1. падающий, отраженный и преломленный лучи лежат в одной плоскости — плоскости падения.
2. [~n0~n] = [~nR~n] → sin Θ0 = sin ΘR → Θ0 = ΘR .
Это закон отражения: угол падения равен углу отражения (зеркальное
отражение).
3. k1 [~n0~n] = k2 [~nT ~n] → k1 sin Θ0 = k2 sin Ψ.
При равенстве импедансов двух сред (Z1 = Z2 ) получим закон преломления Снеллиуса.
Закон преломления Снеллиуса
Закон преломления Снеллиуса следует из необходимости равенства фазовых скоростей вдоль границы раздела двух сред для всех волн (падающей,
отраженной и преломлённой). Отсюда следует условие равенства импедансов
двух сред вдоль границы раздела этих сред. Таким образом, когда Z1 = Z2 ,
для волновых чисел можем записать:
√
√
√
√
k1 = ω µ0 ε0 µ1 ε1 ; k2 = ω µ0 ε0 µ2 ε2 .
(4.3)
Учтём, что скорость света в вакууме
c= √
1
µ0 ε0
.
√
√
Обозначим через n1 = µ1 ε1 и n2 = µ2 ε2 показатели преломления
относительно вакуума.
С учётом этого перепишем (4.3) в виде:
k1 =
ω
c
n1 ,
k2 =
ω
c
n2 .
99.
99Тогда закон преломления Снеллиуса можем записать в виде:
sin Θ k2
n2
=
= .
sin Ψ k1
n1
(4.4)
Зеркальное отражение возникает благодаря интерференции волн, излучаемых электронами на границе раздела сред, находящимися под действием падающей волны. Направление зеркального отражения луча является направлением, соответствующим максимуму нулевого порядка в интерференционной картине. Если расстояние между атомами среды меньше длины волны
падающего излучения, наблюдается лишь один максимум под углом, соответствующим зеркальному углу.
4.2
Отражение при горизонтальной поляризации падающей
волны
~ иH
~ электромагнитного поля в слуРассмотрим ориентацию векторов E
чае горизонтальной поляризации падающей волны.
~ при отражении и
Рисунок 4.4 — Ориентация вектора магнитного поля H
преломлении электромагнитной волны
~ 0, H
~ R, H
~ T — магнитные компоненты падающей, отраНа рисунке 4.4 H
женной и преломленной волн; Θ0 , ΘR , Ψ — углы падения, отражения, преломления; ~n0 , ~nR , ~nT — единичные векторы в направлении распространения
падающей, отраженной и преломленной волн.
Для анализа воспользуемся первой парой граничных условий, рассмотренных нами в подразделе 4.1.1. С учетом законов отражения и преломления
100.
100эти условия перепишутся так:
s
k12 2
(H0 − HR ) cos Θ0 = HT 1 − 2 sin Θ0 ;
k2
k1
µ1 (H0 + HR ) sin Θ0 = µ2 HT sin Θ0 .
k2
(4.5)
При получении уравнений (4.5) учтено, что
s
p
(H0 − HR ) cos Θ0 = HT cos Ψ = HT 1 − sin2 Ψ = HT
k12 2
1 − 2 sin Θ0 ,
k2
Hτ1 = H0 cos Θ0 , Hτ2 = −HR cos Θ0 .
Введем в рассмотрение коэффициенты отражения и преломления при
горизонтальной поляризации падающей волны (так называемые коэффициенты Френеля)
R⊥ =
HR
H0
и r⊥ =
HT
H0
Решая систему уравнений (4.5), получим:
p
µ2 k10 cos Θ0 − µ1 k22 − k12 sin2 Θ0
p
R⊥ =
.
µ2 k10 cos Θ0 + µ1 k22 − k12 sin2 Θ0
(4.6)
p
p
Здесь k10 = ω µ1 ε01 и k20 = ω µ2 ε02 , а ε01 и ε02 — комплексные диэлектрические
постоянные.
Выражение для r⊥ получается аналогично, далее мы его рассматривать
не будем.
В общем случае R⊥ — комплексная величина. Ее можно представить в
виде:
R⊥ = |R⊥ | e−iϕ⊥ ,
|R⊥ | — модуль, ϕ⊥ — аргумент коэффициента отражения.
При отражении волны фаза изменяется на угол ϕ⊥ . Можно представить
H–составляющую отраженной волны в виде
HR = Hτ1 R⊥ = H0 R⊥ exp [−iωt + ik10 (~n0~r) − iϕ⊥ ] .
101.
101В практике радиосвязи, рассматривая задачу отражения от поверхности
Земли (например, при анализе диаграмм направленности антенн), можно для
воздуха (среда 1) положить σ1 = 0, µ1 = µ0 , ε1 = ε0 . Для Земли (среда
2) в большинстве случаев µ2 = µ0 . В этом случае выражение (4.6) можно
переписать в виде:
√
sin A − ε0 − cos2 A
√
R⊥ =
,
(4.7)
sin A + ε0 − cos2 A
ε2
σ2
где A = 90°−Θ0 — угол скольжения, ε0 = − i
= ε − i(60λ)σ — комплексε0 ωε0
ная относительная диэлектрическая проницаемость.
Таким образом, величина R⊥ в приведенном примере зависит от угла
скольжения, длины волны, параметров почвы.
4.3
Отражение при вертикальной поляризации падающей
волны
~ 0, E
~ R, E
~ T для этого случая приведена на рисунОриентация векторов E
ке 4.5. Коэффициент отражения равен
Rk =
ER
.
E0
~ при отражении и
Рисунок 4.5 — Ориентация вектора электрического поля E
преломлении вертикально поляризованной электромагнитной волны
102.
102По аналогии со случаем горизонтальной поляризации, заменив µ2 на ε02
и µ1 на ε01 , получим:
k10 ε02 sin A − ε01
p
k22 − k12 cos2 A
p
Rk = 0 0
= Rk e−iϕk .
0
2
2
k1 ε2 sin A + ε1 k2 − k1 cos2 A
(4.8)
Если, например, мы рассматриваем падение радиоволны из воздуха на
землю, то для воздуха (среда 1) можно положить σ1 = 0, µ1 = µ0 , ε1 ≈ 0.
Для земли (среда 2) — µ2 = µ0 , тогда:
√
ε0 sin A − ε0 − cos2 A
√
Rk =
.
ε0 sin A + ε0 − cos2 A
4.4
(4.9)
Коэффициенты отражения для различных сред
Проанализируем коэффициенты отражения для трех видов среды 2. Первую
среду считаем вакуумом (воздухом).
4.4.1
Среда 2 — диэлектрик
В этом случае для второй среды λσ ε.
Рассмотрим случай горизонтальной поляризации. Здесь коэффициент
|R⊥ | — вещественная величина. Зависимость |R⊥ | и ϕ⊥ от угла скольжения
A приведена на рисунке 4.6.
Рисунок 4.6 — Зависимость модуля |R⊥ | (левая панель) и аргумента ϕ⊥ (правая панель) коэффициента отражения от угла скольжения A при горизонтальной поляризации падающей волны
103.
103Исходя из соотношения (4.7), понятно, что при A = 0 коэффициент отπ
ражения будет равен R⊥ = −1. При A = коэффициент отражения будет
2
√
ε−1
R⊥ = − √
.
ε+1
Фаза при отражении изменяется на π, как видно из рисунка 4.6.
Рассмотрим случай вертикальной поляризации (рисунок 4.7).
В этом случае коэффициент отражения будет равен:
√
ε sin A − ε − cos2 A
√
.
Rk =
ε sin A + ε − cos2 A
(4.10)
Рисунок 4.7 — Зависимость Rk и ϕk от угла скольжения A при вертикальной
поляризации
Из выражения (4.10) следует, что при A = 0 коэффициент отражения
π
будет равен Rk = −1, а при A = :
2
√
ε−1
Rk = √
ε+1
Из рисунка 4.7 хорошо видно, что при некотором угле A = A0 коэффициент отражения Rk = 0. Угол A0 называют углом Брюстера (угол полного
преломления).
104.
104Для того, чтобы Rk = 0, должно выполнятся равенство:
p
1
ε sin A0 = ε − cos2 A0 → sin A0 = √
.
ε+1
(4.11)
При угле A = A0 отражение отсутствует и вся электромагнитная энергия проходит в среду 2. При угле полного преломления имеет место полное
согласование импедансов сред 1 и 2, что и приводит к отсутствию отражения.
При угле падения Брюстера выполняется условие θk + ψ = 90°. Электроны в среде 2 находятся под действием преломленной волны и колеблются
~ T ). При
в направлениях, перпендикулярных преломленному лучу (вектор H
угле падения θk компонента движения электронов, параллельная плоскости
чертежа, направлена по лучу ~nR . Поэтому ее вклад в излучение в этом направлении равен нулю. Это приводит к тому, что отраженная волна полностью поляризована в направлении, перпендикулярном плоскости чертежа.
В частности, эта особенность лежит в основе построения таких интересных устройств, как георадар (показан на рисунке 4.8).
Рисунок 4.8 — Георадар. Рисунок является гиперссылкой на YouTube–ресурс.
Для просмотра видео необходимо подключение к INTERNET
105.
1054.4.2
Среда 2 — полупроводник
Пусть среда 2 является полупроводником, т. е. λσ ≈ ε.
В случае горизонтальной поляризации падающей волны коэффициент
отражения будет комплексной величиной, зависимость модуля и аргумента
комплексного коэффициента отражения от угла скольжения A представлена
на рисунке 4.9.
Рисунок 4.9 — Зависимость |R⊥ | и ϕ⊥ от угла скольжения A при горизонтальной поляризации
Для случая вертикальной поляризации подающей волны поведение модуля и аргумента комплексного коэффициента отражения приведены на рисунке 4.10.
Рисунок 4.10 — Изменение Rk и ϕk от угла скольжения A для вертикальной
поляризации падающей волны
106.
106Характер изменения Rk и ϕk такой же, как и для диэлектрика, но Rk
в ноль не обращается, т. е. угла полного преломления нет.
4.4.3
Среда 2 — проводник
В заключении рассмотрим случай, когда среда 2 является проводником,
т. е. λσ ε.
В этом случае коэффициент отражения также будет комплексной величиной. Зависимость модуля и аргумента коэффициента отражения от угла
скольжения A для случаев горизонтальной и вертикальной поляризации падающей волны показана на рисунке 4.11.
Рисунок 4.11 — Модули коэффициентов отражения и аргументы для двух
случаев поляризации падающего излучения
В случае горизонтальной поляризации падающей волны R⊥ = −1 для
всех углов A, т. е. вся энергия, падающая на границу раздела, отражается.
Электромагнитная энергия в проводник не преломляется.
В случае вертикальной поляризации падающей волны Rk ≈ −1 для всех
A. Энергия падающей электромагнитной волны также полностью отражается.
π
Как видно из рисунка 4.11 при углах A = 0 и A =
2
|R⊥ | = Rk .
Для произвольных значений A
|R⊥ | > Rk .
107.
107Поэтому в радиолокации, например, используют антенны с горизонтальной поляризацией, т. к. для них коэффициент отражения от Земли выше, чем
для антенн с вертикальной поляризацией. Для сравнения на рисунке приведены коэффициенты отражения и фаза для двух случаев поляризации падающего излучения.
4.5
Влияние шероховатости отражающей поверхности
Выражения для коэффициентов R⊥ и Rk были получены в предположении ровной отражающей поверхности, по крайней мере, в пределах области формирования отраженной волны. Однако реальная земная поверхность
никогда не бывает абсолютно гладкой. Даже равнинная местность покрыта
большим числом хаотически расположенных неровностей. Если небольшие
неровности в среднем расположены равномерно, такую поверхность называют шероховатой (для УКВ это, например, взволнованная поверхность моря; для СВ и ДВ — небольшие холмы и здания). Отражение от неровной
поверхности является рассеянным, поэтому напряженность поля в направлении зеркального отражения будет меньше, чем для гладкой поверхности.
Это ослабление можно учесть с помощью эффективного коэффициента отражения Rэфф , расчет которого достаточно сложен. Качественно «гладкость»
поверхности можно оценить с помощью критерия Релея.
4.5.1
Критерий Релея
Пусть плоская волна отражается от неровной поверхности с максимальным размером неоднородностей h, как показано на рисунке 4.12. Часть мощ-
Рисунок 4.12 — К выводу критерия Релея
108.
108ности падающей волны отразится на верхнем уровне (b), часть — на нижнем
(a). Плоскость m − m0 является плоскостью равных фаз падающей волны.
Определим фазовые отношения на плоскости, перпендикулярной направлению отражения волны n − n0 . Наибольшая разность фаз ∆ϕ будет между
волнами, отраженными в точках D и B. Разность хода лучей mDn и m0 Bn0
∆r = ABC = 2AB = 2h sin(θ),
отсюда
4πh
sin θ.
λ
Считается, что отражающую поверхность можно считать гладкой, если допустимые фазовые искажения на плоскости n − n0
∆ϕ = k∆r =
∆ϕдоп =
4πhдоп sin(θ) π
< ,
c
2
отсюда, собственно, критерий Релея
h < hдоп =
λ
8 sin(θ)
(4.12)
Из (4.12) следует, что чем более полога траектория и чем больше λ,
тем слабее возмущающее действие неровностей. Например, для волны длиной
λ = 10 см при угле скольжения 5° hдоп = 14 см, а при уменьшении θ до 0.5°
hдоп возрастает до 1.4 м.
Критерий Релея носит приближенный характер, поскольку не учитывает
форму неровностей, вид поляризации и т. п. Однако качественно он правильно оценивает степень шероховатости отражающих поверхностей.
4.5.2
Закон Ламберта
Если отражающая поверхность является матовой, т. е. покрыта неоднородностями с h > hдоп по Рэлею, наблюдается диффузное, или рассеянное,
отражение, при котором «яркость» отражающей поверхности во всех направлениях при равных углах скольжения примерно одинакова (рисунок 4.13).
Зависимость интенсивности J рассеянного сигнала от угла ϕ описывается
законом Ламберта
J = J0 cos(ϕ),
(4.13)
109.
109Рисунок 4.13 — Иллюстрация к закону Ламберта
здесь J0 — значение J при ϕ = 0. Закон Ламберта был установлен в результате экспериментальных исследований яркости светящихся поверхностей. Закон Ламберта выполняется при наличии следующих условий:
1. концентрация неровностей постоянна на всей отражающей поверхности,
2. отражающая поверхность в среднем не отклоняется от плоскости,
3. неоднородности не создают теневых областей, что справедливо, если
размеры неоднородностей 6 λ.
Отражающая поверхность Земли не бывает идеально гладкой или только шероховатой, поэтому отражение радиоволн зачастую носит полурассеянный характер с максимумом в направлении зеркального отражения (рисунок 4.14).
Рисунок 4.14 — Полурассеянное отражение
Чем короче волна, тем вероятнее выполнение условий, при которых отражение близко к диффузному. Это в первую очередь относится к сантиметровым и более коротким волнам.
110.
1104.6
Отражение при произвольной поляризации падающей
волны
~ иH
~ падающей волны произвольно
Рассмотрим случай, когда векторы E
ориентированы относительно плоскости падения. Для того, чтобы определить
поле отраженной волны, разложим вектор E~0 падающей волны на составляющие в плоскости падения и перпендикулярно плоскости падения. Можно
считать, что падающая волна раскладывается на две волны: вертикально по~ k и горизонтально поляризованную E
~ ⊥.
ляризованную с напряженностью E
Отраженная волна есть результат сложения соответствующих отраженных
волн.
Можно записать:
~1 ,
~1 = E
~1 + E
E
⊥
k
~R .
~R = E
~R + E
E
⊥
k
(4.14)
~ 1 . Используем систему координат с осью
~ R = R⊥ E
~1 и E
~ R = Rk E
Здесь E
⊥
⊥
k
k
~
~ R и осью OZ, совпадаOX, совпадающей с направлением ER⊥ , осью OY — с E
k
ющей с направлением распространения отраженной волны, как это показано
на рисунке 4.15.
Рисунок 4.15 — Отражение при произвольной поляризации падающей волны
Пусть падающая волна:
~1 = E
~ 0 ei(ωt−kz) .
E
111.
111Тогда
ERx = |R⊥ | E0x cos (ωt − kz − ϕ⊥ − ψ)
ERy = Rk E0y cos ωt − kz − ϕk − ψ ,
(4.15)
ψ — фаза колебаний падающей волны в точке падения. Уравнения при фиксированном z представляют уравнение эллипса (за один период в плоскости
z = const вектор описывает эллипс в плоскости XY ), как это показано на
рисунке 4.16.
Рисунок 4.16 — Эллиптическая поляризация электрической компоненты
электромагнитной волны
Рассмотрим частные случаи:
1. Граница раздела — проводник или диэлектрик: ϕ⊥ + ϕk = 0 или π. Эллипс превращается в линию, т.е. мы получили линейную поляризацию.
При угле полного преломления отраженная волна, как бы ни был ори~ падающей волны, всегда горизонтально поляризоентирован вектор E
вана. Поэтому угол θk называют углом полной поляризации.
2. Граница раздела сред — полупроводник. Разность фаз ϕ⊥ +ϕk принимает значения от 0 до π. Отраженная волна эллиптически поляризована.
В частном случае ϕ⊥ + ϕk = π и |R⊥ | E0x = Rk E0y получаем волну с
круговой поляризацией.
112.
112ТЕМА 5
Электромагнитные волны в волноводе
5.1
Общий вид решения волновых уравнений в волноводе
Рассмотрим регулярный волновод, имеющий сечение в поперечной плоскости , одинаковое вдоль оси z, как показано на рисунке 5.1. Положим, что
потери энергии в металлических стенках и заполняющей среде отсутствуют
(т. е. σ = 0).
Рисунок 5.1 — Регулярный волновод
Полученные ранее волновые уравнения для векторов напряженностей
~ иH
~ эквивалентны шести скалярным
электрического и магнитного полей E
уравнениям д’Аламбера для проекций и для среды без потерь (т. е. σ = 0)
имеют следующую структуру:
∆F + k 2 F = 0,
(5.1)
здесь под F (x, y, z, t) нужно понимать любую из проекций вектора электрического или магнитного поля на координатные оси. Будем считать, что электрическое и магнитное поля изменяются по гармоническому закону
F (t) ∼ exp(iωt).
Из проведенного ранее анализа волновых процессов понятно, что поля
в волноводе можно представить в общем виде как суперпозицию падающих
и отраженных волн, которые распространяются вдоль волноводов (ось z), и
искать решение волновых уравнений в виде:
F (x, y, z, t) = F + (x, y)ei(ωt−Kz) + F − (x, y)ei(ωt+Kz) .
(5.2)
113.
113Необходимо принять допущение, что волновое число в волноводе имеет
величину K 6= k, то есть считать, что в общем случае в волноводе длина
2π
2π
не равняется длине волны λ =
в свободном пространстве и
волны Λ =
K
k
ω
соответственно фазовая скорость vф =
волны вдоль волновода отличается
K
ω
от скорости света c = . Подобная ситуация имеет место при наклонном
k
падении плоской волны на отражающую поверхность.
Функции F ± (x, y) характеризуют распределение полей в поперечной плоскости волновода и играют роль амплитуд падающей и отраженной волн. Эти
функции подобны и отличаются только постоянным множителем, так как
удовлетворяют одному и тому же дифференциальному уравнению. Если зависимость полей от продольной координаты определена, то вид волновых
уравнений упрощается.
∂
= ±iK, а
Подставим (5.2) в волновые уравнения (5.1) и учтем, что
∂z
∂2
= −K 2 , получим
2
∂z
∆x,y F ± (x, y) + k 2 − K 2 F ± (x, y) = 0.
(5.3)
Здесь ∆x,y — оператор Лапласа, который включает в себя производные только
по поперечным координатам.
Функции F ± (x, y), характеризующие распределение полей в поперечном
сечении волновода, подобны. Поэтому для выяснения их общих закономерностей достаточно ограничиться рассмотрением лишь падающей волны. Уравнение типа (5.3) в частных производных удобно решать методом разделения
переменных.
Обозначим F + (x, y) = X(x)Y (y), выполним процедуру разделения переменных и получим вместо (5.3) два уравнения:
d2 X
d2 Y
dx
dy 2
+ kx2 X = 0,
2
+ ky2 Y = 0.
(5.4)
114.
114Здесь через kx и ky обозначены так называемые постоянные разделения, для
которых выполняется равенство kx2 + ky2 = k 2 − K 2 , или
kx2 + ky2 + K 2 = k 2
(5.5)
и которые иногда называют (по аналогии с k и K) поперечными волновыми
числами, несмотря на то, что в поперечном направлении распространения
волн не происходит.
Решение уравнений (5.4) можно представить в виде гармонических функций:
sin
sin
X(x) = Cx
(kx x + ϕx ) , Y (y) = Cy
(ky y + ϕy ) .
cos
cos
Двойная запись означает, что исходя из удобства, можно выбирать любую из функций, пока постоянные интегрирования ϕx и ϕy не определены.
Полученные выражения позволяют записать общий вид решения волновых уравнений для любой из составляющих электрического и магнитного
полей в форме
F + (x, y) = C +
sin
sin
(kx x + ϕx )
(ky y + ϕy ) .
cos
cos
(5.6)
Выражение (5.6) показывает, что гармонические изменения напряженности аналогичны полям стоячей волны в поперечном сечении, а в продольном
направлении в волноводе существует волновой процесс, который характеризуется продольным волновым числом K. Постоянные интегрирования ϕx и
ϕy и постоянные разделения kx и ky обычно находятся из граничных условий,
которые могут быть сформулированы для каждого конкретного волновода.
5.2
Дисперсия в волноводах
Определим, что означает отличие волновых чисел в волноводе и свободном пространстве. Для этого обозначим разницу (k 2 − K 2 ) выражением
!2
2π
, которое по форме совпадает с выражением для волновых чисел чеλкр
рез соответствующие длины волн. Сократив все члены этого равенства на
115.
115(2π)2 , получим
1
λ2кр
=
1
1
−
, откуда
λ2 Λ2
Λ=v
u
u
t1 −
λ
(5.7)
!2 .
λ
λкр
Поскольку фазовая скорость распространения волны в волноводе связана с длиной волны в волноводе соотношением vф = Λf (f — линейная
частота), то
c
(5.8)
vф = v
!2 .
u
u
λ
t1 −
λкр
Поясним физический смысл величины λкр .
В выражении (5.8) заменим под корнем отношение длин волн обратным
отношением соответствующих частот (fкр = c/λкр ) и запишем:
c
vф = v
u
u
t1 −
Λ=v
u
u
t1 −
fкр
!2 ,
f
λ
v
u
u
K = k t1 −
fкр
(5.9)
!2 ,
f
fкр
f
!2
.
Первое из соотношений (5.9) показывает, что фазовая скорость зависит
от частоты, и характеризует закон дисперсии для волновода, который изображен графиком на рисунке 5.2.
Важной особенностью этой зависимости является то, что в волноводе
vф > c. Не менее важная особенность данного закона связана с тем, что
116.
116Рисунок 5.2 — Закон волновой дисперсии в волноводе
действительные значения фазовой скорости, а значит, и нормальное распространение электромагнитных волн по волноводу возможно лишь для области
частот f > fкр .
Таким образом, критическая частота (fкр ) — это предельная частота, которая разделяет диапазон нормального распространения электромагнитных
полей в виде волн и так называемый диапазон отсечки (f < fкр ). Критическая длина волны (λкр ) — это некоторое предельное значение длины волны
(измеренное в свободном пространстве). Условие распространения в терминах длин волн формулируется в виде неравенства λ < λкр , однако длина
волны в волноводе другая, чем (на той же частоте) в свободном пространстве; она всегда больше (Λ > λ), и при приближении к критическому режиму
стремится к бесконечности.
5.2.1
Режим отсечки
Если будем пытаться возбуждать волновод на частоте ниже критической, то в соответствии с (5.9) фазовая скорость, длина волны, а значит, и
волновое число в волноводе должны быть мнимыми величинами. Поэтому
волновые множители в (5.2) принимают форму e±Kz eiωt , которая показывает, что составляющие поля во всех точках волновода колеблются синфазно
во времени, а амплитуда колебаний вдоль волновода уменьшается экспоненциально. Это явление не является следствием поглощения, так как оно наблюдается в волноводах без потерь.
117.
117Кроме рассмотренного в данном разделе явления, дисперсия в волноводе
возможна также за счет потерь в стенках волновода или в заполняющем
диэлектрике подобно тому, как это имеет место в случае плоской волны.
5.3
Типы волн в волноводах
Для выяснения вопроса о классификации волн по разным типам сделаем
сначала некоторые формальные превращения. Воспользуемся выражениями
уравнений Максвелла в проекциях на оси координат и будем считать для
упрощения, что в волноводе распространяется только падающая волна. Это
не изменит общность выводов, так как функции F + (x, y) и F − (x, y) подобны.
Поскольку характер изменения полей вдоль оси задается выражением
F (x, y, z, t) = F + (x, y)ei(ωt−Kz) + F − (x, y)ei(ωt+Kz) ,
то в уравнениях Максвелла примем, что
∂
= −iK.
∂z
Теперь получим выражения для поперечных составляющих поля, выраженные через продольные составляющие:
−i
Ex =
;
(k 2 − K 2 )
−i
Hy =
∂Hz
z
ωε ∂E
∂x + K ∂y
;
(k 2 − K 2 )
−i
Ey =
∂Hz
z
K ∂E
∂y + ωµ ∂x
∂Hz
z
ωε ∂E
∂y + K ∂x
(k 2 − K 2 )
(5.10)
;
(k 2 − K 2 )
−i
Hx =
∂Hz
z
K ∂E
∂x + ωµ ∂y
.
Первое слагаемое в числителе определяется продольной составляющей
электрического поля, второе — продольной составляющей магнитного поля.
Т. е. возможно существование таких волн, в которых отсутствует продольная
118.
118составляющая или электрического, или магнитного поля. Таким образом, выделяют две группы волн — T E–волны и T M –волны.
Волны T E типа
Характеризуются отсутствием продольной составляющей электрического поля (Ez = 0, «магнитные волны»). Одна из особенностей таких волн
состоит в том, что отношение поперечных составляющих электрического и
магнитного полей не зависит от координат. Это отношение называется волновым сопротивлением волновода, причем
Z0T E =
Ey
Ex
E⊥
ZC
ωµ
Λ
=
=
= ZC = r
=
2 .
Hy
Hx
H⊥
K
λ
f
1 − fкр
(5.11)
Волны T M типа
Характеризуются отсутствием продольной составляющей магнитного поля (Hz = 0, «электрические волны»). Волновое сопротивление волновода для
этих волн
s
2
E
K
E
λ
fкр
E
⊥
y
x
=
=
=
= ZC = ZC 1 −
.
(5.12)
Z0T M =
Hy
Hx
H⊥
ωε
Λ
f
Волны T EM типа
Возможно ли существование таких электромагнитных волн, в которых
обе продольные составляющие отсутствуют (Ez = Hz = 0)?
Да, возможно! В случае, когда K → k, т. е. когда знаменатель в уравнениях (5.10) также обращается в нуль.
Такие волны называются T EM –волнами, и необходимым условием их
существования является K = k. Для таких волн характерно отсутствие дисперсии (vф = c).
Целесообразность проведенной классификации заключается в том, что
сравнительно легко можно количественно анализировать лишь отдельные типы волн, а любые сложные поля можно подать как их суперпозицию.
119.
1195.3.1
Условия существования бездисперсионных волн
в волноводе
Формулы (5.9) справедливы, если (k 2 − K 2 ) > 0. Именно это неравенство
было исходным для последующих выводов о характере дисперсии в волноводах. И если возможно существование бездисперсионных волн, то необходимым условием этого является равенство K = k. Оно означает, что скорость
распространения таких волн равна скорости света (vф = c) в среде, которая
заполняет волновод, и длина волны в волноводе равна длине волны в свободном пространстве (Λ = λ). Эти же равенства можно получить, если в (5.9)
формально принять λкр → ∞, или fкр → 0.
Принимая во внимание физическое содержание fкр , можно сделать вывод, что волны без дисперсии не имеют режима отсечки, то есть их распространение в волноводе возможно на любых частотах, включая самые низкие.
О характере полей в волноводе без дисперсии можно судить из уравнения
(5.3), если в нем принять k = K:
∆x,y F ± (x, y) = 0.
(5.13)
Данное выражение по форме совпадает с двумерным уравнением Лапласа,
которое описывает статические поля. Но поскольку граничные условия на
стенках волновода и для переменных, и для статических полей одинаковы,
можно сделать следующие выводы.
Во–первых, характер распределения полей в поперечном сечении волновода для волн без дисперсии такой же, как и для статических полей.
Во–вторых, распространение волн без дисперсии возможно лишь в волноводах, которые допускают существование статических полей. К ним относятся такие линии передачи, как коаксиальный волновод, полосковая
линия и тому подобные, которые имеют как минимум два проводника
и допускают присоединение источника постоянного напряжения.
5.4
Прямоугольный волновод
Самая простая модель для количественного исследования процессов распространения электромагнитных волн в волноводах — прямоугольный вол-
120.
120новод, то есть металлическая труба с прямоугольным поперечным сечением
размерами a × b.
Рисунок 5.3 — Прямоугольный волновод с поперечным сечением a × b
Прямоугольные волноводы широко используются при передаче электромагнитных волн в сантиметровом и миллиметровом диапазонах, особенно при
высоких уровнях мощности. Для упрощения будем считать, что потери в
стенках волновода и в заполняющем его диэлектрике отсутствуют. Это даёт
возможность проще сформулировать граничные условия: на стенках волновода отсутствует касательная составляющая электрического поля (Ez = Ey = 0
при x = 0 и x = a; Ez = Ex = 0 пpи y = 0 и y = b).
Чтобы не определять постоянные интегрирования для каждой составляющей поля, воспользуемся таким приемом: запишем выражения для продольной составляющей поля в форме
F + (x, y) = C +
sin
sin
(kx x + ϕx )
(ky y + ϕy ) ,
cos
cos
(5.14)
а поперечные найдем из соотношений (5.10).
Тогда можно обойтись без формулировки граничных условий для магнитного поля. Допущение о бесконечной длине волновода позволяет рассматривать лишь падающую волну.
5.4.1
T E–волны (Ez = 0)
Запишем выражение для амплитуды (волновой множитель опускаем)
продольной составляющей магнитного поля:
Hz = iH0 cos (kx x + ϕx ) cos (ky y + ϕy )
(5.15)
121.
121Подставляя (5.15) в (5.10), получаем выражения для поперечных составляющих:
H0 ky ωµ cos (kx x + ϕx ) sin (ky y + ϕy )
Ex = −
;
(k 2 − K 2 )
H0 kx ωµ sin (kx x + ϕx ) cos (ky y + ϕy )
Ey = −
;
(k 2 − K 2 )
(5.16)
H0 ky K sin (kx x + ϕx ) cos (ky y + ϕy )
;
Hx = −
(k 2 − K 2 )
H0 kx K cos (kx x + ϕx ) sin (ky y + ϕy )
Hy = −
.
(k 2 − K 2 )
В соответствии с граничными условиями принимаем, что
mπ
- Ey = 0 при x = 0 и x = a, тогда ϕx = 0 и kx =
, где m = 0, 1, 2, 3 . . . ;
a
- Ex = 0 на широких стенках волновода (y = 0, y = b), тогда ϕy = 0 и
nπ
ky =
, где n = 0, 1, 2, 3 . . . .
b
Определение постоянных интегрирования и постоянных разделения позволяет получить выражения для T E–волн:
nπx
H0 Z0T E ky K cos mπx
sin
a
b
Ex = −
;
2
2
kx + ky
nπx
sin
H0 Z0T E kx K cos mπx
a
b
;
Ey = −
2
2
kx + ky
nπx
H0 kx K sin mπx
cos
a
b
Hx = −
;
2
2
kx + ky
nπx
H0 ky K cos mπx
sin
a
b
Hy = −
;
2
2
kx + ky
mπx
nπx
Hz = iH0 cos
cos
.
a
b
(5.17)
Постоянная H0 может быть определена из начальных условий или, например, при известной мощности, которая передается по волноводу.
Очень важный результат полученного решения заключается в том, что в
волноводе возможно распространение бесконечного множества разных типов (мод) волн, каждая из которых характеризуется определенной парой значений чисел m и n и обозначается
T Emn.
122.
122В некоторых источниках применяется еще и такое обозначение:
Hmn.
Из выражений (5.17) легко понять физическое содержание чисел m и n:
они показывают количество полупериодов поля, которое укладывается соответственно вдоль широкой и узкой стенок волновода.
Эти числа могут независимо друг от друга принимать любые целые положительные значения. Исключением является случай одновременного равенства m = 0 и n = 0, когда все поперечные составляющие принимают
нулевые значения. Самую простую конфигурацию полей имеют, естественно,
типы волн с наименьшими индексами.
Рисунок 5.4 — Характерные функции распределения продольной составляющей электрического поля в поперечном сечении волновода для некоторых
мод
Второй важный результат заключается в том, что определение постоянных kx и ky позволяет из равенства
kx2 + ky2 + K 2 = k 2
найти критическую длину волны
2
λкр = v
!2
u
u m
t
+
a
!2 ,
n
b
которая зависит от типа волны и размеров волновода.
(5.18)
123.
1235.4.2
T M –волны (Hz = 0)
В данном случае удобно выбрать выражение для продольной составляющей электрического поля в форме
Ez = iE0 sin (kx x + ϕx ) sin (ky y + ϕy ) .
(5.19)
Поперечные составляющие определяются при подстановке Ez в (5.10):
E0 kx K cos (kx x + ϕx ) sin (ky y + ϕy )
;
k2 − K 2
E0 ky K sin (kx x + ϕx ) cos (ky y + ϕy )
Ey =
;
k2 − K 2
E0 ky ωε sin (kx x + ϕx ) cos (ky y + ϕy )
Hx = −
;
k2 − K 2
E0 kx ωε cos (kx x + ϕx ) sin (ky y + ϕy )
Hy = −
.
k2 − K 2
Ex =
(5.20)
Выбор Ez в форме (5.19) удобен тем, что использование граничных условий приводит к тем же значениям постоянных интегрирования (ϕx = ϕy = 0)
nπ
и постоянных разделения (kx = mπ
a , ky = b ). Окончательные выражения для
составляющих после подстановки постоянных принимают вид
nπy
sin
E0 kx K cos mπx
a
b
;
Ex =
2
2
kx + ky
nπx
E0 ky K sin mπx
cos
a
b
Ey =
;
2
2
kx + ky
mπx
nπy
Ez = iE0 sin
sin
;
a
b
mπy
nπy
E0 ky K sin a cos b
Hx = − T M ·
;
kx2 + ky2
Z0
nπy
mπy
E0 kx K cos a sin b
Hy = − T M ·
.
kx2 + ky2
Z0
(5.21)
Здесь, как и для T E–волн, возможно бесконечное множество волноводных мод, которые обозначаются
T Mmn.
124.
124Также по аналогии с T E–волной в некоторых источниках применяется
такое обозначение:
Emn.
Существенное отличие лишь в том, что для T M –волн невозможны нулевые значения ни одного из индексов m и n, так как при этом Ez = 0, а
значит, будут равны нулю и все другие составляющие полей. Выражение для
расчета критической длины волны такое же, как и для волн T Emn .
Рисунок 5.5 — Характерные функции распределения продольной составляющей электрического поля в поперечном сечении волновода для некоторых
мод. Числа m и n определяют количество полупериодов стоячей волны вдоль
широкой и узкой стенок соответственно
5.5
5.5.1
Одномодовый диапазон
Основная мода
Используя полученные результаты, рассмотрим некоторые общие закономерности распространения разных мод в волноводах и правила для выбора
геометрических размеров волновода. Как правило волновод используют в так
называемом одномодовом режиме, то есть на тех частотах, на которых в волноводе может распространяться лишь одна мода волн.
Для нахождения этого диапазона рассмотрим диаграмму, представленную на рисунке 5.6, для которой по оси частот нанесены значения
fкр =
c
,
λкр
которые могут быть рассчитаны по значениям λкр для разных индексов m и
n (выражение (5.18)).
125.
125Рисунок 5.6 — Определение одномодового диапазона по критическим частотам волноводных мод
Как видно из рисунка 5.6, наименьшее значение fкр будет иметь волна
T E10 . Остальные моды имеют большие значения fкр , их взаимное расположение будет зависеть от соотношения размеров a и b. Если a > 2b, то ближай01
20
10
. Заметим, что некоторые моды
, в противном случае fкр
будет fкр
шим к fкр
имеют одинаковые значения fкр (например, T E11 и T M11 ), они называются
вырожденными.
а)
б)
Рисунок 5.7 — Возбуждение прямоугольного волновода с соотношением сторон a > 2b в одномодовом режиме
Если возбуждать волновод на некоторой частоте fген , как это показано
на рисунке 5.7 а), то в волноводе будут распространяться лишь моды T E10 ,
126.
126mn
< fген .
T E20 , T E01 , для которых выполняется условие распространения fкр
Для остальных мод будет наблюдаться режим отсечки.
При уменьшении частоты возбуждения в режим отсечки попадают волны T E01 , потом T E20 и последней T E10 , как показано на рисунке 5.7 б). Отсюда ясно, что лишь для волны T E10 можно найти диапазон частот, в котором
она сможет распространяться без примеси других волн. Поэтому мода T E10
называется основной, а остальные — высшими.
Диапазон одномодового режима волновода лежит в границах от fкр основной моды до fкр ближайшей высшей моды, как показано на рисунке 5.6.
Следовательно, нетрудно рассчитать геометрические размеры a и b волновода, который обеспечивает передачу электромагнитных волн в заданном диапазоне частот. Однако необходимо помнить, что реальный диапазон несколько у́же рассмотренного, т. к. при использовании волновода в режиме, близком
к критическому, существенно увеличиваются потери энергии и растет поглощение волны.
Учитывая особенное значение моды T E10 , в завершение охарактеризуем
распределение её полей. Аналитические выражения для составляющих поля
легко получить из (5.17) при m = 1, n = 0:
Ex = 0;
Hy = 0;
πx
2a
;
Ey = H0 ZC sin
Λ a
πx
2a
;
Hx = −H0 sin
Λ a
πx
Hz = iH0 cos
.
a
(5.22)
На рисунке 5.8 изображена «фотография» силовых линий электрического и магнитного поля, а на рисунке 5.9 — векторные поля. Электрические силовые линии имеют лишь одну составляющую и соединяют широкие
стенки. Наибольшее значение Ey имеет в центре волновода, а на боковых
стенках уменьшается до нуля. Магнитные силовые линии представляют собой замкнутые линии, которые лежат в плоскостях, параллельных широким
стенкам.
Важной особенностью является то, что положения максимумов поперечных составляющих E и H совпадают. В этих же точках имеет максимальное
127.
127Рисунок 5.8 — Различные проекции распределения силовых линий электрического (красные линии) и магнитного (зеленые линии) поля
значение и продольная составляющая вектора Пойнтинга. С течением времени вся картина перемещается вдоль оси z с фазовой скоростью:
vф = v
u
u
t1 −
c
λ
!2 .
2a
При приближении частоты к критическому значению длина волны в волноводе, то есть и пространственный период поля, возрастает до бесконечности, составляющая Hx → 0 и магнитное поле становится продольным, а колебания во всех точках волновода происходят синфазно. Вектор Пойнтинга
для такого режима определяется только составляющими Hz и Ey и будет направлен перпендикулярно к оси волновода. Это значит, что передачи энергии
по волноводу не происходит.
128.
128Рисунок 5.9 — Распределение векторов Пойнтинга, электрического и магнитного поля, плотности поверхностного тока на широкой стенке волновода для
основной моды T E10
5.5.2
Коаксиальный волновод
Коаксиальный волновод — наиболее распространенная линия передачи.
Используются как твердые, наполненные воздухом волноводы, так и гибкие, с
диэлектрическим заполнением (коаксиальные кабели). С коаксиальными кабелями студенты Института физики знакомы достаточно хорошо, так как
постоянно приходится иметь с ними дело при выполнении всевозможных лабораторных работ.
Однако твердые коаксиальные волноводы встречаются не так часто. Поэтому для знакомства с ними на рисунке 5.10 приведены фотографии антеннофидерной системы Иркутского рада некогерентного рассеяния, расположенного в 120 км к северо-востоку от Иркутска. Радары некогерентного рассея-
129.
129ния — весьма сложные и дорогостоящие установки, мировая сеть насчитывает
лишь 9 таких инструментов. Под эгидой Международного радиосоюза (УРСИ) с их помощью ведутся регулярные координированные наблюдения по
Программе мировых дней. Получаемые при этом экспериментальные данные
составляют основу для широкого спектра исследований по солнечно-земной
физике.
Мощность радара в импульсе достигает 2.5–3.2 МВт, длительность импульса составляет 140–820 мкс, частота повторения импульсов 24.4 Гц.
а)
б)
Рисунок 5.10 — Система фидеров, подводящих энергию к антенной системе
Иркутского радара некогерентного рассеяния (а); антенная система Иркутского радара некогерентного рассеяния, представляет собой секторальный
рупор (б)
Еще один пример использования твёрдых коаксиальных волноводов приведен на фотографии, представленной на рисунке 5.11. Необходимо сказать,
что подобных «нагревных» стендов, способных создать в ионосфере плазменные неоднородности электронной концентрации, в Мире осталось всего
три. Один из них находится в России, это стенд «СУРА»1 , расположенный
недалеко от рабочего посёлка Васильсурск в Нижегородской области; второй
— HAARP2 , самый мощный из существующих, располагается в США (штат
Аляска); третий стенд — EISCAT, расположен в северной Европе. В частности, стенд EISCAT интересен ещё и тем, что представленная на рисунке 5.11
1
2
Стенд Универсальный РАдиофизический
High frequency Active Auroral Research Program
130.
130его фидерная система состоит из твердых коаксиальных линий, которые заполнены инертным газом.
Рисунок 5.11 — Система фидеров, подводящих энергию к антенной системе нагревного стенда EISCAT (European Incoherent SCATter Scientific
Association). Место расположения Тро́мсё, Норвегия (69,50 с.ш., 190 в.д.).
Максимальная эффективная излучаемая мощность — Pэфф = 1,2 ГВт. Частотный диапазон: 3,8 ÷ 8 МГц
Основным типом волны для коаксиального волновода является T EM –
волна, которая характеризуется отсутствием дисперсии и как следствие —
равенством фазовой скорости и скорости света для данной диэлектрической
среды. Характер распределения полей в поперечной плоскости для бегущих
T EM –волн совпадает с распределением статических полей и находится из
уравнения Лапласа.
Получить аналитическое выражение для полей T EM –волны можно, рассматривая в выражениях для статических полей ток и напряжение как мгновенные значения, которые равны соответствующим амплитудам, умноженным на волновой множитель:
Vm
D
E=
cos (ωt − kz) ;
ln
r
d
(5.23)
Im
H=
cos (ωt − kz) .
2πr
131.
131Рисунок 5.12 — Распределение электрического (красные линии) и магнитного
(зеленые линии) полей для основной T EM моды в поперечном сечении коаксиального волновода аналогично их распределениям для статических полей
~ иH
~ и характер их изменения в пространстве
Направление векторов E
для фиксированного момента времени показаны на рисунке 5.12. С течением
времени вся картина распределения полей смещается вдоль оси z со скоростью света. Важным параметром коаксиальных линий является так называемое эквивалентное волновое сопротивление, которое в данном случае определяется как отношение амплитуд напряжения и тока для падающей волны.
Учитывая, что для T EM –волн отношения амплитуд E и H равняется волновому сопротивлению среды (3.52), из (5.23) получаем
s
Z0 = 60
µ
ε
ln
D
d
!
[Ом].
(5.24)
Коаксиальный волновод можно использовать для любых частот, включая постоянный ток. Однако на высоких частотах, как и в прямоугольном
волноводе, в нем могут возбуждаться высшие моды T E и T M типов. Поэтому верхняя частота использования ограничена ближайшей высшей модой T E11 , которая имеет критическую длину волны, приблизительно равную
длине средней окружности поперечного сечения коаксиальной линии. По этой
причине для более высокочастотных волноводов нужно выбирать меньшие
поперечные размеры, а это вызывает дополнительные потери энергии. Поэтому, особенно для волноводов с диэлектрическим заполнением, диапазон
их использования может ограничиваться допустимым затуханием.
132.
132ТЕМА 6
Радиоволны в неоднородных средах
В реальных условиях наличие хорошо проводящих поверхностей, а также неоднородностей различного происхождения как на Земле, так в атмосфере и космосе (имеется ввиду межпланетное пространство), существенно
искажает прямолинейное распространение радиоволн.
Влияние данных факторов приводит к следующим основным механизмам распространения волн.
Дифракция — отклонение распространения радиоволн от прямолинейного,
обусловленное наличием препятствий на их пути. Чем больше длина
волны, тем больше напряженность поля в области тени.
Рефракция — отклонение распространения радиоволн от прямолинейного,
обусловленное изменением диэлектрической проницаемости ε среды на
пути распространения.
Атмосфера и космос — весьма сложные по своим электрическим характеристикам среды. Здесь, по большей части, наблюдается явление рефракции.
Факторы, определяющие неоднородности, различны даже в пределах одной
атмосферы. Однако в большинстве случаев неоднородности таковы, что характер их влияния на распространение радиоволн одинаков, независимо от
того, в какой части атмосферы или космоса они имеют место.
В тропосфере с высотой изменяются давление, температура, влажность,
что вызывает рефракцию радиоволн. Наличие в тропосфере случайных неоднородностей турбулентного происхождения приводит к рассеянию радиоволн
и, как следствие, к возможности их распространения далеко за пределы прямой видимости.
В стратосфере распространение радиоволн аналогично тропосферному,
однако эффекты атмосферного влияния выражены значительно слабее.
Ионосфера оказывает существенное влияние на распространение радиоволн. Так, радиоволны с λ = 10 м обычно отражаются от ионосферных слоёв
и возвращаются на расстоянии до 3500 ÷ 4000 км от точки излучения, затем
отражаются от Земли и т. д., то есть могут распространяться скачками на
большие расстояния, вплоть до кругосветного. В диапазоне УКВ ионосфе-
133.
133ра прозрачна, и радиолуч уходит в космос, однако часть его энергии рассеивается различными ионосферными неоднородностями (метеорные следы,
турбулентные неоднородности, спорадические слои и т. д.).
При распространении радиоволн вдоль поверхности земли превалирующую роль играет явление дифракции. Особенно важную роль данное явление
играет при распространении радиоволн в урбанизированной (гродской) среде.
Городская среда создает специфические условия для распространения радиоволн. Теневые зоны, многократные отражения и рассеяние волн формируют
многолучевые поля со сложной интерференционной структурой и резкими
пространственными изменениями уровня сигнала.
Моделирование влияния перечисленных факторов на распространения
радиоволн можно осуществлять различными способами: детерминированными, статистическими и комбинированными. К первым относят в основном методы геометрической оптики, физической и геометрической теорий дифракции, метод параболического уравнения, а также численные методы электродинамики. Они позволяют произвести расчеты напряженности поля с большой степенью точности, но предъявляют высокие требования к точности задания модели среды. Статистические методы учитывают случайный характер распределения неоднородностей среды, оказывающих влияние на процесс
распространения радиоволн. Они позволяют предсказать некоторые средние
характеристики сигналов.
В рамках настоящего лекционного курса будет рассмотрено только геометрооптическое приближение.
6.1
Геометрооптическое приближение
Рассмотрим неоднородную среду, полагая что показатель преломления
заметно изменяется лишь на расстояниях L λc (где λc — длина волны в
среде) .
Естественным выглядит предположение, что структура решения волно~
вого уравнения будет похожа на решение для однородных сред. Векторы E,
~ ~k будут медленно изменяться в зависимости от координат. Масштаб L буH,
дет масштабом, где эти изменения можно считать существенными. Т.е. среду
можно считать локально однородной на масштабе длины волны λc и существенно неоднородной на расстояниях, превышающих L.
134.
134Для того, чтобы относительные изменения показателя преломления n =
n(xyz) на масштабе, равном длине волны λc в среде, были пренебрежимо
малыми, должно выполняться условие
1 dn
λ
λc 1. Учтём, что λc = .
n ds
n
Получим условие применимости геометрической оптики:
1 dn
n2 ds
(6.1)
λ 1.
Задачу о распространении волны в неоднородной среде в геометрическом приближении можно сформулировать следующим образом. В однородной среде n = const и плоская волна описывается выражением:
~ =E
~ 0 ei(ω·t−kc s) = E
~ 0 ei(ω·t−k·n·s) , kc = kn =
E
2π
λc
.
(6.2)
Изменение фазы на отрезке длиной s равно kn. В неоднородной среде
показатель преломления является функцией координат n = n(xyz). Если выбрать малый участок пути ∆s, то на нем показатель преломления n(s) изменяется незначительно, и для изменения фазы волны справедливо выражение
kn(s)∆s. Изменение фазы волны на всем пути распространения определится
R
интегралом n(s)ds.
Если использовать лучевую трактовку, то выражение (6.2) для волны
следует переписать в виде:
~ =E
~ 0e
E
6.1.1
R
i ω·t−k n(s)ds
l
.
(6.3)
Уравнение луча
Выведем уравнение луча. Касательная к лучу в какой-либо точке ортогональна поверхности равных фаз, проходящей через эту точку. В однородных средах лучи — прямые линии, поверхности равных фаз — плоскости.
Уравнение поверхности равных фаз в таких средах определяется выражением ωt − kx = const.
135.
135В неоднородных средах лучи криволинейны, и поверхности равных фаз
не являются плоскостями. Уравнение поверхности равных фаз в этом случае
представим в виде:
ω · t − kψ(xyz) = const.
(6.4)
Рисунок 6.1 — Поверхности равных фаз в неоднородной среде
Поверхности ψ(xyz) = const перпендикулярны касательным к лучам.
Найдем скорость распространения постоянной фазы вдоль луча s. Для этого
продифференцируем уравнение (6.4) для поверхности равных фаз по t:
ω−k
∂ψ ∂s
∂s ∂t
(6.5)
= 0.
Обозначим через ~l единичный вектор, направленный по касательной к
лучу в направлении возрастания функции ψ. Можно записать:
v
u
u ∂ψ 2 ∂ψ 2
∂ψ
= s · grad(ψ) = |grad(ψ)| = t
+
+
∂l
∂x
∂y
∂ψ
!2
∂z
.
(6.6)
Из (6.5) и (6.6) для скорости получим:
v=
ω
ds
=
.
dt
k |grad(ψ)|
С другой стороны, значение v можно получить из уравнения
Z
ω · t − k nds = const.
(6.7)
136.
136Дифференцируя это уравнение по времени, получим: ω − k · n
v=
ds
dt
=
ds
dt
= 0, отсюда
ω
.
k·n
(6.8)
Таким образом, из соотношений (6.7) и (6.8) получаем:
(6.9)
n = |grad(ψ)| .
Функция ψ, определяемая уравнением (6.9), называется эйконалом (фазой)1 ,
а само уравнение — уравнением эйконала.
Получим уравнение луча, используя уравнение эйконала. Для этого умножим обе части выражения (6.9) на единичный вектор ~l.
~l · n = ~l · |grad(ψ)| = grad(ψ).
(6.10)
Продифференцируем уравнение (6.10) по s:
∂
∂ ~
l · n = grad(ψ).
∂s
∂s
Найдем производную вектора ~l вдоль кривой s:
!
∂ 2ψ
∂ 2ψ
∂ 2ψ
grad(ψ) = ~l∇ grad(ψ) = ~i lx 2 + ly
+ lz
+
∂s
∂x
∂y∂x
∂z∂x
!
!
∂ 2ψ
∂ 2ψ
∂ 2ψ
∂ 2ψ
∂ 2ψ
∂ 2ψ
+~j lx
+ ly 2 + lz
+ ~k lx
+ ly
+ lz 2 .
∂x∂y
∂y
∂z∂y
∂x∂z
∂y∂z
∂z
∂
(6.11)
Из (6.10) следует:
lx =
1 ∂ψ
n ∂x
,
ly =
1 ∂ψ
n ∂y
,
lz =
1 ∂ψ
n ∂z
.
Подставляя эти выражения в уравнения (6.11), получим уравнение луча.
1
Название происходит от древнегреческого слова эйкон — изображение.
137.
137Продемонстрируем решение на примере первого слагаемого в правой части уравнения (6.11):
lx
∂ 2ψ
∂ 2ψ
"
1 ∂ψ ∂ 2 ψ
∂ψ ∂ 2 ψ
∂ψ ∂ 2 ψ
#
+ lz
=
+
+
=
∂y∂x
∂z∂x n ∂x ∂x2 ∂y ∂y∂x ∂z ∂z∂x
!2
!2
!2
1 ∂
∂ψ
∂ψ
∂ψ
1 ∂ 2 ∂n
=
=
+
+
· n =
.
2n ∂x
∂x
∂y
∂z
2n ∂x
∂x
∂x2
+ ly
∂ 2ψ
Аналогично для других слагаемых получим
Поэтому
∂n ∂n
,
.
∂y ∂z
∂
~
grad(ψ) = grad(n) = ∇n.
∂s
Отсюда уравнение луча
∂ ~ ~
l · n = ∇n.
∂s
6.1.2
(6.12)
Геометрическая оптика слоисто–неоднородной среды
В случае, когда свойства среды (коэффициент её преломления) неодинаковы в разных местах, т. е. когда среда неоднородна, волна преломляется и
движется по криволинейной траектории. Чем более неоднородна среда, чем
резче изменяется коэффициент преломления, тем больше кривизна траектории (рисунок 6.2).
Рисунок 6.2 — Искривление траектории распространения волны в неоднородной среде
138.
138Явление искривления траектории распространения волны в неоднородной среде называется рефракцией.
В качестве примера рассмотрим траектории лучей в сферически–слоистой
и плоско–слоистой средах. Примерами таких сред могут служить земная атмосфера и ионосфера.
Уравнение луча в сферически–слоистой среде
В сферически слоистой среде показатель преломления зависит только от
расстояния ~r до фиксированной точки O:
n = n (~r) .
В этом случае вектор grad(n) направлен по радиусам ~r, проведенным из начала системы координат, как это показано на рисунке 6.3.
Рисунок 6.3 — Рефракция луча в сферически слоистой среде
Умножим обе части уравнения луча (6.12) векторно на ~r:
h
i
∂ ~
~
~r,
l · n = ~r, ∇n = 0.
∂s
Учтем, что
Вектор
∂~r
∂s
(6.13)
∂ h ~i
∂~r ~
∂ ~
~r, nl =
, nl + ~r,
nl .
∂s
∂s
∂s
"
касателен к лучу, т. е. параллелен ~l, поэтому
∂~r
∂s
#
, n~l = 0.
139.
139Следовательно, уравнение (6.13) можно записать в виде
∂ h ~i
~r, nl = 0.
∂s
Это означает, что векторное произведение вектора n~l, касательного к лучу, и
вектора ~r остается постоянным вдоль луча:
h
i
~
~r, nl = const.
Отсюда следует, что лучи являются плоскими кривыми, лежащими в
плоскости, проходящей через начало координат. Вдоль каждого из лучей выполняется условие:
n · ~r sin(θ) = const,
(6.14)
где θ — угол между касательными к лучу n~l в данной точке и радиус-вектором
~r, что видно из рисунка 6.3. Данное соотношение представляет собой закон
Снелиуса для сферически слоистой среды.
Константа определяется из граничных условий. Пусть при
~r = ~r0 , sin(θ) = sin(θ0 ), n = n0 = 1.
Тогда
n · ~r sin(θ) = ~r0 sin(θ0 ).
(6.15)
Рисунок 6.4 — Рефракция луча в сферически слоистой среде. К пояснению
выражения (6.16)
140.
140Уравнение траектории можно найти из соотношения (смотри рисунок 6.4):
tan(θ) =
rdα
sin(θ)
sin(θ0 )
.
=
=s
dr
cos(θ)
n2 r2
− sin2 (θ0 )
2
r0
(6.16)
Уравнение луча в плоско–слоистой среде
В плоско–слоистой среде показатель преломления зависит от одной координаты, например n = n(z). В этом случае уравнение луча можно записать
в виде:
d (n sin(θ)) dn
=
= 0,
ds
dx
или
n(z) sin(θ(z)) = const = sin(θ0 ),
(6.17)
где θ — угол между осью z и касательной ~l в любой точке траектории. В
начале координат, при z = 0, угол θ будет равен углу θ0 .
Рисунок 6.5 — Рефракция луча в плоско–слоистой среде
Уравнение луча получим из соотношения (рисунок 6.5):
tg(θ) =
dx
sin(θ0 )
=p
dz
n2 − sin2 (θ0 )
(6.18)
Из полученных соотношений видно, что угол наклона луча по мере распространения в слоистой среде изменяется, т. е. лучи искривляются.
141.
1416.2
Рефракция лучей в плоско–слоистой среде
Рассмотрим несколько примеров рефракции лучей при разных законах
изменения показателя преломления от высоты n = n(z).
6.2.1
Случай монотонного увеличения показателя
преломления с высотой
В этом случае grad(n) > 0, как это показано на рисунке 6.6. Такие условия могут быть реализованы, например, в тропосфере. Пусть в точке M неоднородной среды на высоте zm над идеально отражающей плоской поверхностью выходит луч под углом Θ0 к вертикали. Поведение луча будет зависеть
от угла. При анализе надо опираться на уравнение (6.18).
π
Если θ0 < , луч направлен вверх в сторону увеличивающихся значений
2
показателя преломления. В уравнении (6.18) знаменатель при увеличении
высоты увеличивается и tg θ — уменьшается. Это приводит к искривлению
луча и он приближается к вертикали (кривая 1 на рисунке 6.6).
Рисунок 6.6 — Рефракция луча в плоско–слоистой среде. Случай монотонного
увеличения показателя преломления с высотой
π
Если θ0 > луч будет направлен к отражающей поверхности. Распро2
странение происходит в сторону уменьшающихся значений показателя преломления. В уравнении (6.18) уменьшается знаменатель, что приводит к увеличению tg θ, т. е. к уменьшению θ. Следовательно, луч отклоняется от вертикали, и при этом возможны различные варианты распространения (траектории 2–4 на рисунке 6.6).
Кривая 2: луч достигает уровня z = 0 и отражается.
Кривая 3: луч достигает точки поворота при выполнении условия n(z) =
|sin θ|. Это возможно, когда θ = π2 . Сначала луч становится параллель-
142.
142ным оси x, а затем поворачивается в сторону возрастающих значений
n(z).
Кривая 4: при некотором значении угла точка поворота θ > π2 будет лежать
на поверхности z = 0.
Кривая 4 является границей между областью, в которую лучи в результате
рефракции не могут попасть, и называются областью тени.
6.2.2
Случай монотонного уменьшения показателя
преломления с высотой
В этом случае grad(n) < 0, как это показано на рисунке 6.7. Такие условия характерны для ионосферы. В результате рефракции лучи отклоняются к горизонтали, т. к. угол θ > θ0 . На высоте z0 , определяемой из условия
n (z0 ) = sin θ0 , направление луча параллельно горизонтальной плоскости, т. е.
на высоте z0 происходит поворот луча. Из уравнения (6.18) следует, что
z
Zz0
Z0
p
p
sin θ0 n2 − sin2 θ0 dz + sin θ0 n2 − sin2 θ0 dz.
0
z
x=
Рисунок 6.7 — Рефракция луча в плоско–слоистой среде. Случай монотонного
уменьшения показателя преломления с высотой
Расстояние между точками входа луча в неоднородную среду и выхода из нее (т. е. длина скачка при распространении радиоволн в ионосфере,
например) равно:
Zz0 p
δx = x2 − x1 = 2 sin θ0
n2 − sin2 θ0 dz.
0
143.
1436.3
Условия применимости геометрической оптики
Условие малости длины волны в среде по отношению к характерному
λ
масштабу изменения параметров волны и среды 1 (а именно это и ознаL
чает условие (6.1)) является необходимым, но недостаточным условием справедливости геометрооптического приближения.
Возможности аналитически определить условие применимости метода и
его погрешностей ограничены тем, что в задачах о распространении волн в
неоднородных средах не известно точное решение. Кравцовым Ю. А. и Орловым Ю. М. предложены эвристические критерии применимости приближения
геометрической оптики2 .
Представим, что точечный источник волн расположен в точке с радиусвектором ~r1 , a точка наблюдения в находится в точке с радиус–вектором ~r2 .
Эйконал (или оптический путь) вдоль луча ~r1~r2 обозначим ψ(~r1~r2 ) и будем
считать его опорным лучом. Выберем точку ~r10 , лежащую возле опорного
луча, и соединим точку ~r10 с ~r1 и ~r2 . Ломаный луч ~r1 − ~r10 − ~r2 назовем виртуальным лучом (смотри рисунок 6.8).
Рисунок 6.8 — Построение границ пространственных зон Френеля для рефрагирующей в неоднородной среде волны
Оптический путь вдоль виртуального луча равен
ψвирт = ψ (~r1 , ~r10 ) + ψ (~r10 , ~r2 ) .
2
Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. – М.: Наука, 1980. – 305 с.
144.
144Построим около опорного луча поверхность
(ψвирт − ψопорн ) =
λc
,
2
где λc — длина волны в среде.
В этом случае эйконал на опорном луче отличается от эйконала на виртуальном луче на половину длины волны (т.е. их фазы отличаются на π) .
Эта поверхность представляет огибающую первых зон Френеля, нанизанных
на опорный луч (смотри подраздел 3.4). Уравнение этой поверхности можно
представить в виде:
F (~r0 ) = |ψ (~r1~r0 ) + ψ (~r0~r2 ) − ψ (~r1~r2 )| −
λc
= 0.
2
Объем, ограниченный этой поверхностью, можно назвать френелевским объемом. В частном случае плоской волны в однородной среде (т.е. когда n =
const) радиус первой зоны Френеля равен:
r
af ≈
λc z
.
n
Зонам более высокого порядка в уравнении для поверхности F (r0 ) = 0
mλc
отвечает разность хода
, m = 2, 3, . . .. Если свойства изменяются плавно,
2
вследствие интерференции вторичные волны от высших зон Френеля взаимно
погашаются, и результирующее поле определяется ближайшей окрестностью
луча — его френелевским объемом.
Таким образом, становится очевидным различие между математическим
лучом (это бесконечно тонкая линия) и физическим лучом, имеющим конечную толщину, определяемую френелевским объемом.
6.3.1
Критерии применимости геометрической оптики
Исходя из того, что френелевский объем определяет область пространства, формирующего поле в заданной точке, можно сформулировать два критерия применимости метода геометрической оптики.
1. Параметры среды и волны (амплитуда и градиент фазы) не должны
заметно изменяться в поперечном сечении френелевского объема.
145.
1452. френелевские объемы лучей, приходящих в одну и ту же точку, не
должны существенно пересекаться друг с другом.
Согласно критерию 1, должны выполняться условия:
∇⊥ A
1,
- для амплитуды волны A: af
A
- для компонент импульса p = ∇ψ: af
- для показателя преломления n: af
∇⊥ p
p
1,
∇⊥ n
1,
n
где af — максимальное сечение френелевского объема; ∇⊥ = ∇ − l(l∇) —
оператор дифференцирования в направлении, ортогональном лучу.
Критерий 2 означает, что общая часть френелевских объемов лучей δVf ,
приходящих в данную точку наблюдения, должна быть значительно меньше
каждого из френелевских объемов Vf . Критерий 2 позволяет избежать двукратного учета вклада одних и тех же вторичных волн в результирующее
поле.
6.4
Рефракция лучей в сферически–слоистой среде
Рефракцию лучей в сферически–слоистой среде рассмотрим на примере
трансионосферного распространения радиоволн коротковолнового диапазона. Для начала определим электрические параметры среды распространения
радиоволн, т. е. параметры ионосферы.
6.4.1
Электрические параметры ионосферы
Ионосфера представляет собой газ, в котором наряду с нейтральными
частицами находятся положительные и отрицательные ионы. Все частицы
ионосферы постоянно находятся в хаотическом тепловом движении. Движущиеся в ионосфере заряды рассматривают как некоторый конвекционный
ток. Можно считать, что ионосфера представляет собой квазинейтральный
ионизированный газ (рисунок 6.9).
Отрицательные ионы — это электроны, а положительные ионы — это
атомы или молекулы, у которых не хватает одного или нескольких электронов. При прохождении электромагнитной волны через ионосферу положительные и отрицательные ионы начинают двигаться в такт с изменением
поля волны.
146.
146Рисунок 6.9 — Распределение концентрации плазмы в ионосфере в зависимости от высоты z. Максимум концентрации плазмы Nmax достигается в верхнем слое F на высоте z ≈ 300 км. В дневное время Nmax ≈ 106 см−3 , в ночное
время Nmax ≈ 3 × 105 см−3 . Слои D и E расположены на высотах 60 ÷ 100 км.
Нижний слой D (высота 60 ÷ 80 км) существует только в дневное время
Масса положительного иона водорода в 1840 превосходит массу электрона, а масса положительных ионов других газов в десятки тысяч раз превосходит массу электрона. Поэтому токами, образованными положительными
ионами, можно пренебречь по сравнению с токами, образованными электронами.
Наряду с конвекционным током в поле радиоволны возникает ток смещения в вакууме. Следовательно, плотность тока в ионосфере J~ равна сумме
плотностей тока смещения J~см и конвекционного тока J~эл :
J~ = J~см + J~эл .
147.
147Поле волны в фиксированной точке ионосферы можно представить в
виде:
~ = E0 eiωt .
E
Соответственно плотность тока смещения равна:
J~см = ε0
~
∂E
∂t
~
= iωε0 E.
(6.19)
При наличии в ионосфере электромагнитного поля волны на хаотичное
тепловое движение накладывается упорядоченное движение электронов, вызванное полем волны.
Обозначим скорость движения электронов через v, а их количество в
единице объема (концентрацию) через N , тогда для плотности конвекционного тока запишем:
J~эл = evN.
(6.20)
Полная плотность тока в ионосфере в заданной точке будет равна:
~ + evN.
J~ = iωε0 E
(6.21)
Соответственно второе уравнение Максвелла запишется в виде:
~ + evN.
~ = iωε0 E
rot H
(6.22)
Необходимо определить скорость движения электрона v.
~
Запишем уравнение движения электрона в поле E:
m
dv
dt
+ mνv = eE.
Здесь m = 9.106 × 10−31 кг — масса электрона, ν — число соударений электрона с ионами, атомами и молекулами газа в единицу времени.
Решение уравнения будем искать в виде:
v = A exp(iωt),
148.
148тогда
v=
e
·
1
m jω + ν
~
E.
Следовательно:
~ = iωε0 E
~+
rot H
e2 N
e2 N
!
~
~ = iω ε0 − j
E.
E
m(iω + ν)
mω(iω + ν)
(6.23)
Сопоставим уравнение (6.23) с уравнением Максвелла:
~ = iω D
~ = iωε0a E.
~
rot H
Таким образом, ионизированный газ можно рассматривать как сплошную среду с комплексной диэлектрической проницаемостью
ε0a = ε0 − i
e2 N
σ
= εa − i .
mω(iω + ν)
ω
(6.24)
Данное допущение справедливо, если длина волны больше среднего расстоя1
ния между электронами, т. е. λ N − 3 .
Приравняв левые и правые части в уравнении (6.24), найдем электрические параметры ионосферы:
εa = ε0 − i
e2 N
·
1
m ω2 + ν 2
e2 N
ν
σ=
· 2
.
m ω + ν2
,
(6.25)
Таким образом, относительная диэлектрическая проницаемость ионосферы равна:
e2 N 1
εa
· .
(6.26)
ε= =1−
ε0
mε0 ω 2
Величина e2 N mε0 имеет размерность квадрата частоты и назавается
плазменной частотой, обозначается как ωN .
e2 N
2
= ωN
= (2πfN )2 .
mε0
(6.27)
149.
149Подставим в это выражение числовые параметры:
e = −1.602 · 10−19 [Кл];
m = 9.106 · 10−31 [кг];
Получим:
√
fN =
ε0 =
1
36π
· 10−9
" #
Ф
м
.
(6.28)
80.8N ,
причём здесь N — число электронов в кубическом метре, fN — частота в
герцах.
Следовательно, относительную диэлектрическую проницаемость ионосферы можно представить в виде:
ε=1−
2
ωN
ω2
=1−
fN2
f2
.
(6.29)
- Относительная диэлектрическая проницаемость ионосферы меньше единицы (ε < 1).
- Ионосфера является диспергирующей средой, т. к. величины εa и σ зависят от частоты.
- Ионосфера является неоднородной средой, т. к. величины εa и σ зависят от электронной концентрации (N ), которая изменяется с высотой,
широтой, долготой и т. п.
Таким образом получаем, что показатель преломления в ионосфере изменяется по закону:
s
n=
6.4.2
√
ε=
1−
80.8N (z)
.
f2
(6.30)
Расчет траекторий лучей
После того, как мы получили выражение для зависимости коэффициента
преломления электромагнитной волны от её частоты и высоты над поверхностью Земли, сформулируем условия задачи для расчёта траекторий лучей
в сферически–слоистой ионосфере.
Здесь необходимо сделать одну оговорку. Выражение (6.30) не учитывает
тот факт, что у Земли есть собственное магнитное поле, которое, вообще говоря, необходимо учитывать при расчётах траекторий лучей в ионосфере на
150.
150высотах выше 100 км. Однако учет магнитного поля Земли в расчётных задачах приводит к тому, что в результате различной амбиполярной диффузии в
ионосфере вдоль и поперёк силовых линий магнитного поля возникает необходимость учитывать то, что среда распространения является анизотропной.
Это, в свою очередь, приводит к возникновению двулучепреломления, как
при распространении света через анизотропный кристалл.
Рассмотрение вопросов, связанных с распространением радиоволн в анизотропных средах, выходит за пределы настоящего лекционного курса. Таким
образом, мы рассмотрим случай распространения радиоволн в изотропной
плазме, т. е. без учёта магнитного поля.
Постановка задачи
В качестве примера вычисления траекторий электромагнитной волны в
ионосфере рассмотрим двумерный случай при использовании принципа Ферма в геоцентрических полярных координатах. Влияние магнитного поля Земли и столкновений электронов учитываются учитывать не будем. Таким образом, будем считать среду сферически–неоднородной.
Более того, рассмотрим динамический случай — прохождение солнечного
терминатора вдоль экспериментальной радиотрассы.
Задачу сформулируем таким образом, чтобы можно было считать ионосферу двумерно–неоднородной, т. е. показатель преломления n будет зависеть
от двух геоцентрических координат — расстояния от центра Земли до луча
(~r) и угла (ϕ) между радиус–вектором ~r0 , проведённым из начала координат
к месту, где расположен передатчик, и радиус–вектором ~r, как это показано
на рисунке 6.10.
Рисунок 6.10 — Зависимость показателя преломления от двух геоцентрических координат
151.
151Для численного моделирования была выбрана радиотрасса «Москва —
Зеленодольск». Так как оба пункта лежат примерно на одной широте, то горизонтальным градиентом, связанным с широтой, можно пренебречь, и принимать во внимание только горизонтальный градиент, связанный с местным
временем (долготой).
Рисунок 6.11 — Экспериментальная радиотрасса «Москва (Радиостанция
точного времени) — Зеленодольск (Филиал КФУ)», выбранная для численного моделирования
Кроме этого, в Зеленодольске на базе Филиала КФУ работал экспериментальный автоматизированный приёмный пункт для исследования вариаций
параметров трансионосферных радиосигналов в широком диапазоне частот
(рисунок 6.12). Таким образом, имелась возможность сравнить результаты
моделирования с реальными измерениями.
Рисунок 6.12 — Вид автоматизированного приёмного комплекса, работавшего в Филиале КФУ в г. Зеленодольск. Левая панель — пульт управления и
регистрации; правая панель — антенная система приёмного комплекса
152.
152Параметры ионосферы были рассчитаны при помощи Международной
справочной модели ионосферы (International Reference Ionosphere) IRI–2001.
Для построения модели ионосферы по IRI–2001 был выбран магнитоспокойный день (индекс Ap = 10) весеннего равноденствия 23.03.2007 г. с низкой
солнечной активностью (число солнечных пятен Rz = 0, индекс F10,7 = 75).
Для того, чтобы пояснить порядок дальнейших численных расчетов лучевых траекторий в двумерно–неоднородной среде, необходимо сделать несколько замечаний.
Принцип Ферма
Фронт волны, распространяющейся в неоднородной среде, представляет
собой поверхность постоянного эйконала, т. е. поверхность вида:
ψ(x, y, z) = const.
(6.31)
Лучи в каждой точке нормальны к волновому фронту, и их направление
определяется уравнением эйконала (6.9), как это показано на рисунке 6.13.
Рисунок 6.13 — Направление распространения волны и её фронт в неоднородной среде
Рассмотрим волну, распространяющуюся из точки A в точку B по траектории, изображенной на рисунке 6.14.
Величину ψ в точке A примем за начало отсчёта ψ(A) = 0 и найдем,
чему равна величина ψ(B).
153.
153Рисунок 6.14 — Траектория распространения волны
Для этого разобьём траекторию (луч) на множество маленьких отрезков,
так что в пределах каждого из них луч представлялся бы отрезком прямой
(рисунок 6.14), тогда фаза, набираемая на каждом таком участке, будет равна
~ki ∆~ri ,
где ~ki — волновой вектор, соответствующий данному участку.
Тогда величина ψ(B) определяется выражением:
ψ(B) =
B
X
~ki ∆~ri =
i=A
ZB
~kdl.
(6.32)
A
Теперь предположим, что есть несколько возможных путей S, по которым волна может попасть из точки A в точку B, как это показано на
рисунке 6.15.
Рисунок 6.15 — Несколько возможных траекторий распространения волны
Амплитуда волны в точке B выразится в виде суммы по всем этим путям:
UB =
X
S
eiψS (B) .
(6.33)
154.
154В общем (предельном) случае все возможные пути заполнят всё пространство. Однако в подавляющем большинстве случаев слагаемые в сумме
(6.33) будут очень быстро осциллировать и взаимно уничтожать (гасить) друг
друга. Исключения составят лишь те пути, для которых различие в фазах
ψ(B) составят величину второго порядка малости по отношению к отличию
путей друг от друга. В результате получаем:
UB ≈ eiψS∗ (B) ,
(6.34)
где S ∗ — тот путь, который определяется из условия экстремальности интеграла (6.32)
Z
δψ = δ ~kd~l = 0.
(6.35)
S
Здесь δ означает вариацию интеграла.
Данный принцип называется принципом Ферма.
Метод Гамильтона для расчета траекторий лучей
В общем случае, для расчета нам требуется система дифференциальных
уравнений первого порядка, не обязательно линейных, которая является замкнутой, т. е. имеет вид
dyi
= fi (y1 , y2 , . . . , yn ) ,
dx
i = 1, 2, . . . , n,
dyi
где x является независимой переменной и каждая производная
выражаетdx
ся как функция всех yi . Такая система уравнений может быть проинтегрирована численными стандартными методами. Например, методом Рунге–Кутта
4-го или 5-го порядка.
Показатель преломления n считается действительным и выражается через электронную концентрацию N (~r, ϕ), выражение (6.30).
Из принципа Ферма о стационарности фазового времени распространения (6.35) получаем уравнения Эйлера в сферических координатах ~r, θ, ϕ; l
— некоторая независимая переменная:
155.
1552
dϕ
2
dθ 2
+
sin
ϕ
dl
dl
d
dr
∂n ds
n
−
− nr
= 0,
ds
dl
ds
∂r dl
dl
dθ 2
2
nr
sin
ϕ
cos
ϕ
dϕ
∂n
ds
d
dl
nr2
−
−
= 0,
ds
dl
ds
∂ϕ dl
dl
(6.36)
(6.37)
а из выражения
d
dl
nr2 sin2 ϕ
dθ
ds
!
−
∂n ds
∂θ dl
=0
следует, что лучи лежат в продольной плоскости.
Будем считать, что l есть расстояние вдоль луча. Тогда выполняется
условие, что показатель преломления является функцией лишь ~r и ϕ, т. е.
n = n(~r, ϕ). Положим, что оси, проведенной из центра Земли к передатчику,
соответствует угол ϕ = 0.
Для удобства вычислений введем следующие обозначения:
nr2 dD
dh
, h = r − re , D = re ϕ,
u=n , v=
ds
re ds
где re — радиус Земли.
Тогда первые два уравнения (6.36) и (6.37) принимают вид
dv
ds
= re
∂n
∂D
,
dD
ds
= re
v
nr
,
2
du
ds
=
v2
∂n
nr
∂h
+
3
,
dh
u
= .
ds n
(6.38)
Если луч выходит из точки на поверхности Земли под углом α к горизонту, то начальные условия для системы уравнений можно сформулировать
следующим образом:
h = 0, D = 0,
dD
ds
= cos α,
dh
ds
= sin α.
Решение этой системы обыкновенных дифференциальных уравнений проводилось с системе MatLab методом Руге–Кутта 5-го порядка. Результаты
расчётов приведены на рисунке 6.16.
Из анализа лучевых траекторий, приведенных на рисунке 6.16, можно
сделать несколько выводов.
156.
156(Утренние часы)
Рисунок 6.16 — Результаты расчетов лучевых траекторий для двумерно–
неоднородной ионосферы. Прохождение утреннего терминатора
Во–первых. В начальный период времени (02:00 UT) ни одна из траекторий не попадает в точку приёма, таким образом, в этот момент времени
радиосигнал в п. Зеленодольск не принимается. С течением времени, когда
Солнце восходит над радиотрассой, меняется ионосфера, и в точку приёма попадает всё большее количество лучевых траекторий. Таким образом, напряженность поля становится выше и радиоканал в это время начинает надежно
работать. Очевидно, что в вечерние часы наблюдается обратная картина.
Результаты этих модельных расчётов подтверждаются натурными измерениями (результаты измерений приведены на рисунке 6.17), проведенными на автоматизированном приёмном комплексе, представленном на рисунке 6.12. Как видно из рисунка 6.17, здесь наблюдается периодическая суточная зависимость.
Во–вторых. Из рисунка 6.16 хорошо видно, что в точку приёма может
одновременно прийти сразу несколько лучей, причем каждый из них имеет
своё время распространения и, соотвественно, свой набег фазы. Это, в свою
очередь, приводит к временной и частотной дисперсии, т. е. информационный
сигнал «размазывается» по времени и по частоте.
Пример подобного поведения радиосигнала для высокоширотной радиотрассы Шпицберген — Кируна приведен на рисунке 6.18. Необходимо сказать,
что использовавшийся в данных измерениях автоматический приёмный комплекс позволял измерять вариации напряженности электромагнитного поля,
157.
157Рисунок 6.17 — Вариации напряженности поля, измеренные на радиотрассе
«Москва (Радиостанция точного времени) — Зеленодольск (Филиал КФУ)»
углы приходов радиосигналов, доплеровский сдвиг частоты, а также время
распространения радиосигналов по экспериментальной радиотрассе.
Рисунок 6.18 — Особенности распространения коротковолновых радиосигналов в субавроральной ионосфере
158.
158Высокоширотная ионосфера очень «богата» всевозможными неоднородностями, которые детектируются при помощи специальной сети субавроральных радаров — SuperDARN3 . Результат детектирования подобных ионосферных неоднородностей приведён на левой панели рисунка 6.18, синей линией
показана радиотрасса Шпицберген — Кируна. В правой части рисунка 6.18
показаны вариации напряженности электромагнитного поля (верхняя панель),
а также азимутальный (средняя панель) и вертикальный (нижняя панель) углы прихода радиосигналов. Здесь хорошо видно, что наличие ионосферных
неоднородностей, которые, ко всему прочему, находятся в движении, приводит к возникновению временной и частотной дисперсии в радиоканале.
Подобный характер распространения радиоволн, когда в точку приема
приходят волны с разных направлений и с разными временными задержками, порождает явления межсимвольной интерференции при передаче кодовых последовательностей. Искажения сигнала, обусловленные межсимвольной интерференцией, могут вызывать серьезное ухудшение характеристик
системы и качества высокоскоростной передачи цифровой информации.
Необходимо сказать, что последние десятилетия характеризуются быстрым внедрением цифровых систем связи, предназначенных для передачи подвижным абонентам всевозможных сообщений. При проектировании и эксплуатации подобных связных систем, особенно в городских условиях, необходимо учитывать явления, связанные с дифракцией радиоволн.
6.5
Дифракция радиоволн
Из курса оптики мы хорошо знаем явление дифракции, более того, в
подразделе 3.4 был рассмотрен принцип Гюйгенса–Френеля, описывающий,
в общем случае, дифракцию Френеля на отверстии. В случае, когда величина отверстия (щели) существенно меньше первой зоны Френеля, то при
рассмотрении явления дифракции пользуются приближением Фраунгофера.
Однако при рассмотрении вопросов, связанных с распространением волн радиочастотного диапазона, длина которых много больше длины волн видимого
света, дифракцию можно рассматривать в первоначальной трактовке Юнга,
т. е. как огибание волной препятствия. В современной, более широкой трактовке, к дифракции волн фактически относят все эффекты, возникающие при
3
SuperDARN — Super Dual Auroral Radar Network.
159.
159взаимодействии волн с объектом любых размеров, даже малых по сравнению
с длиной падающей волны λ, когда сопоставление с лучевым приближением совершенно не показательно. При таком общем толковании дифракция
волн тесно переплетается с явлениями распространения и рассеяния волн в
неоднородных средах.
В рамках данного раздела мы рассмотрим только вопросы, связанные с
распространением радиоволн при наличии экранирующих препятствий.
Рисунок 6.19 — Клиновидное препятствие на трассе
Оценим влияние экранирующего препятствия в предположении, что препятствие имеет форму непрозрачного клина. Такая аппроксимация применяется, если размеры препятствия (вершины клина) вдоль трассы много меньше
размера поперечного сечения эллипсоида, существенного для распространения, а размеры поперек трассы много больше этого размера. Пусть такое
препятствие характеризуется высотой экранирования d, равной возвышению
гребня клина над линией прямой видимости, соединяющей точки излучения
A и приема B (рисунок 6.19).
Если пренебречь физическими свойствами клина (σ, µ, ε), то можно
~
свести задачу к оптической дифракции, а именно, напряженность поля E
в точке приёма определяется формулой
~ =E
~ 0 · F,
E
160.
160~ 0 — поле в свободном пространстве, а F — дифракционный мнов которой E
житель
r
~
E
1
C 2 (u) + S 2 (u) iγ
√
F =
=
(C(u) − iS(u)) =
e .
(6.39)
~0
2
2
E
Здесь
√
d 2
u=
,
R1
R1 — радиус первой зоны Френеля;
tg(γ) = −
S(u)
,
C(u)
а S(u) и C(u) — интегралы Френеля:
1
C(u) = −
2
Zu
0
2
πx
dx,
cos
2
1
S(u) = −
2
Zu
πx2
dx.
sin
2
0
Изображение зависимостей S(u) и C(u) от u представляет собой спираль
Корню. Изменчивость множителя F в зависимости от u (по сути, от высоты
экрана, выраженной в зонах Френеля) представлена на рисунке 6.20.
Рисунок 6.20 — Изменчивость дифракционного множителя в зависимости от
высоты экрана
161.
161Дифракционный множитель F флуктуирует около 1 при d < 0, равен
0,5 при d = 0 и плавно понижается до 0 при d > 0.
Полученные результаты позволяют приближённо рассчитывать напряжённость поля на трассах, проходящих над остроконечными холмами и горными кряжами. Отметим, что независимо от формы препятствия с ростом
длины волны дифракционные потери уменьшаются.
6.5.1
Эффект «усиления препятствием»
Эффект «усиления препятствием» наблюдается обычно на трассах УКВ
протяжённостью 100 ÷ 150 км, проходящих через горные кряжи высотой 1 ÷
2 км, и заключается в том, что напряжённость электрического поля радиоволны при некотором удалении от препятствия может оказаться большей, чем
на таком же расстоянии от передающей антенны на трассе без препятствий.
Теоретически эффект усиления радиосигнала вытекает из теоремы Фейнберга: задача о поле излучателя над идеально проводящей землей с выступом
эквивалентна задаче о поле такого же излучателя и его зеркального изображения в свободном пространстве при наличии препятствия, имеющего форму
выступа, состыкованного со своим зеркальным изображением (рисунок 6.21).
Рисунок 6.21 — К объяснению эффекта усиления препятствием
Пусть на трассе имеется клиновидное препятствие (рисунок 6.21), с вершины H которого видны как передающая антенна , так и приемная . В точку
H приходят два луча: прямой (AH) и отраженный от земной поверхности
(ACH). Они возбуждают вершину препятствия, в результате чего в точке B
должна наблюдаться суперпозиция 4-х лучей: двух, возбужденных прямым
162.
162лучом, и двух, возбужденных отраженным лучом. Обозначим длины путей
распространения
r1 = AH + HB,
r2 = AH 0 + H 0 B,
r3 = A0 H + HB,
r4 = A0 H 0 + H 0 B.
Тогда поле в точке приёма B:
~B =
E
4
X
~ i) = E
~ 0m (r1 )FAHB ei(ωt−kr1 ) + E
~ 0m (r2 )FAH 0 B RC RD ei(ωt−kr2 ) +
E(r
i=1
~ 0m (r3 )FA0 HB RC ei(ωt−kr3 ) + E
~ 0m (r2 )FA0 H 0 B RD ei(ωt−kr4 )
+E
и
|EB | = E0m | FAHB e−ikr1 + RC FA0 HB e−ikr2 + RC RD FAH 0 B e−ikr3 +
+ RD F
A0 H 0 B
e
−ikr4
|,
(6.40)
где RC и RD — коэффициенты отражения лучей от почвы в точках C и D.
Практический интерес представляют пологие трассы, когда
RC ≈ RD ≈ −1
и дифракционные множители F мало отличаются друг от друга. В этом случае из (6.40) следует, что
|EB | 6 4E0m ,
т. е. поле радиоволны в точке приема B, находящейся за препятствием, не
может превосходить 4-х кратного значения поля при распространении в свободном пространстве.
Эффект усиления препятствием возможен, если потери при огибании
препятствия не слишком велики. Обычно абсолютное усиление поля невелико, однако если длина трассы значительно превышает расстояние прямой
видимости, так что точка приема при отсутствии препятствия находится в
глубокой тени за горизонтом, эффект усиления может быть значительным.
Практика показывает, что на таких трассах препятствие, выполняющее роль
пассивного ретранслятора, способно увеличить напряжённость поля радиоволны на 60 ÷ 80 дБ по сравнению с дифракционным.
163.
163Список рекомендованной литературы
1. Г. С. Горелик. Колебания и волны. Введение в акустику, радиофизику и
оптику. — М.: Физматлит, 2008.
2. Д. В. Сивухин. Общий курс физики. Учеб. пособие для ВУЗов в 5-ти
томах. Т.III. Электричество. — 4-ое изд., стереот. — М.: Физматлит,
2004. — 656 с.
3. Дж. Пирс. Почти все о волнах. — М.: Мир, 1976.
4. Е. Пейн. Физика колебаний и волн. — М.: Мир, 1979.
5. Ф. Крауфорд. Волны. Берклеевский курс физики. T.3. — М.: Наука,
1984.
6. Ф. Б. Чёрный. Распространение волн. — М: Сов. радио, 1972.
7. М. В. Виноградова, О. В. Руденко, А. П. Сухоруков. Теория волн. — M.:
Наука, 1979.
8. К. А. Путилов. Курс физики. Том I. Механика. Акустика. Молекулярная физика. Термодинамика. — М.: Физматлит, 1963.




















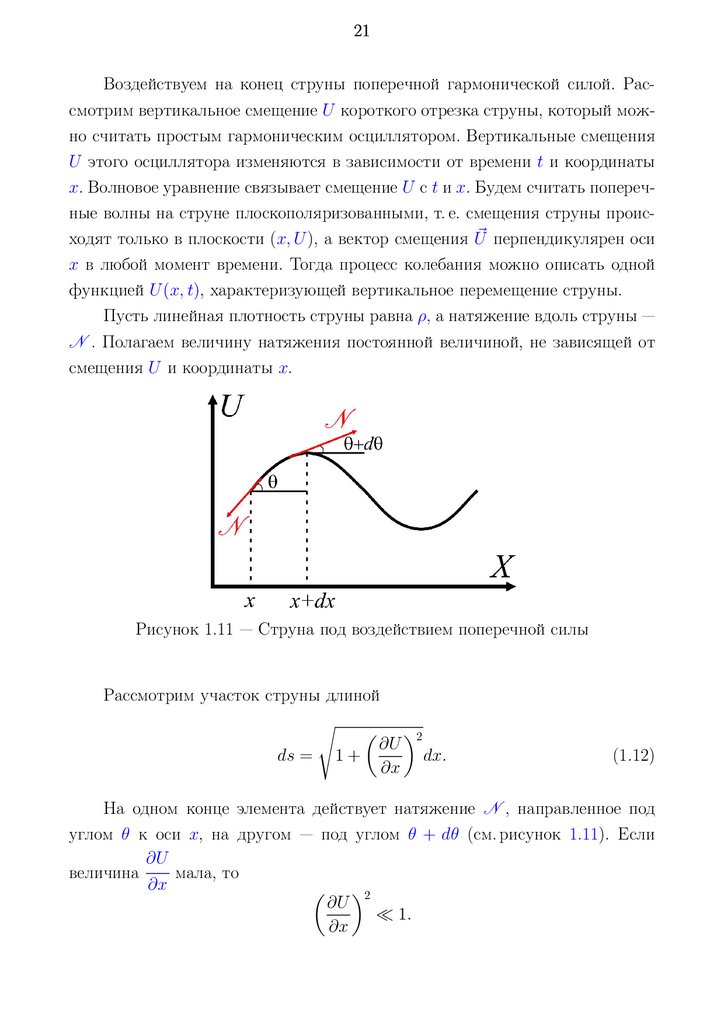






















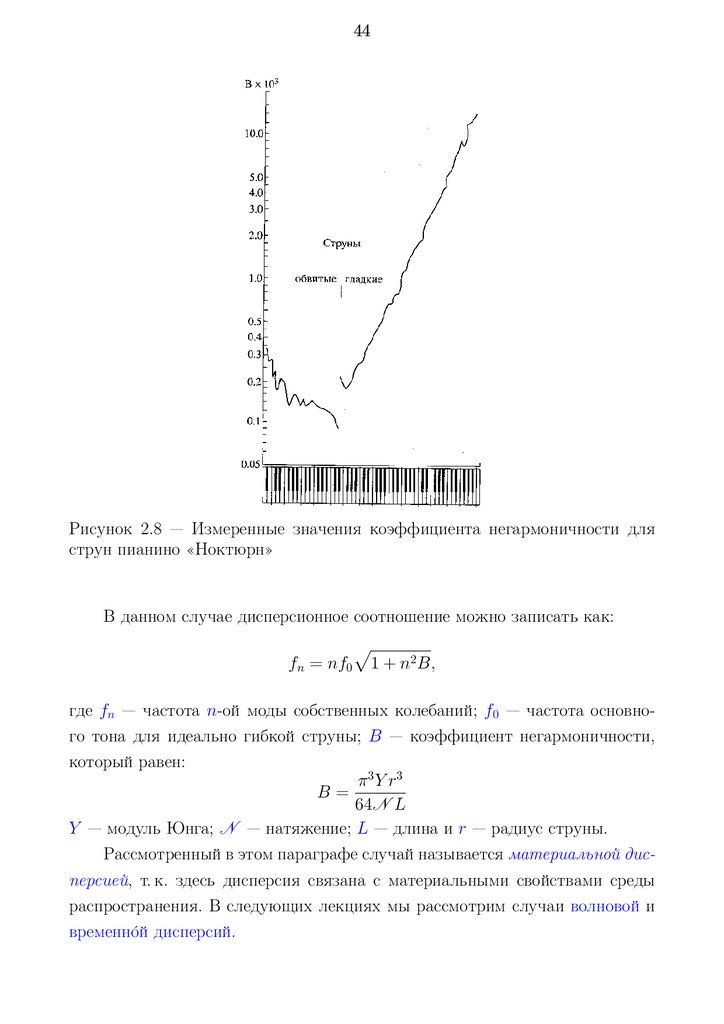
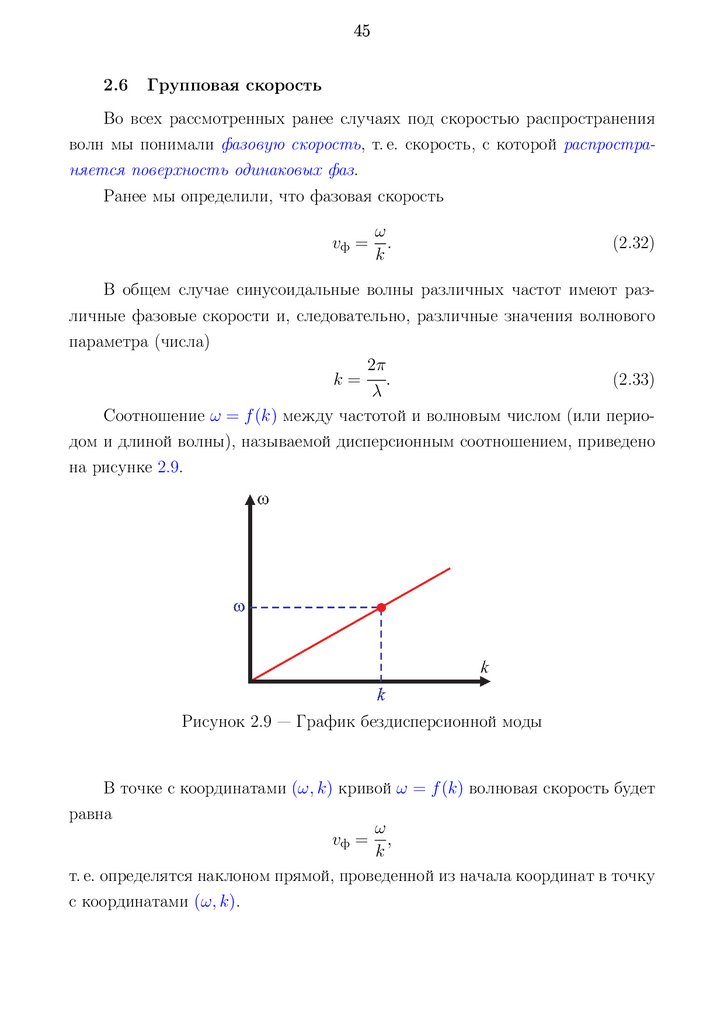
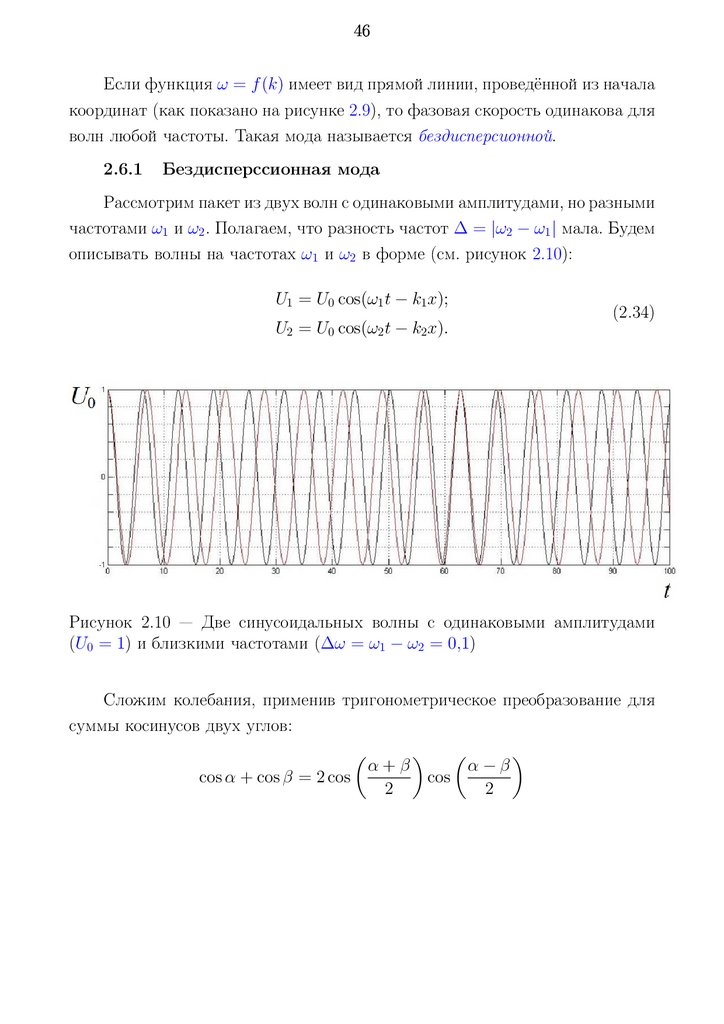



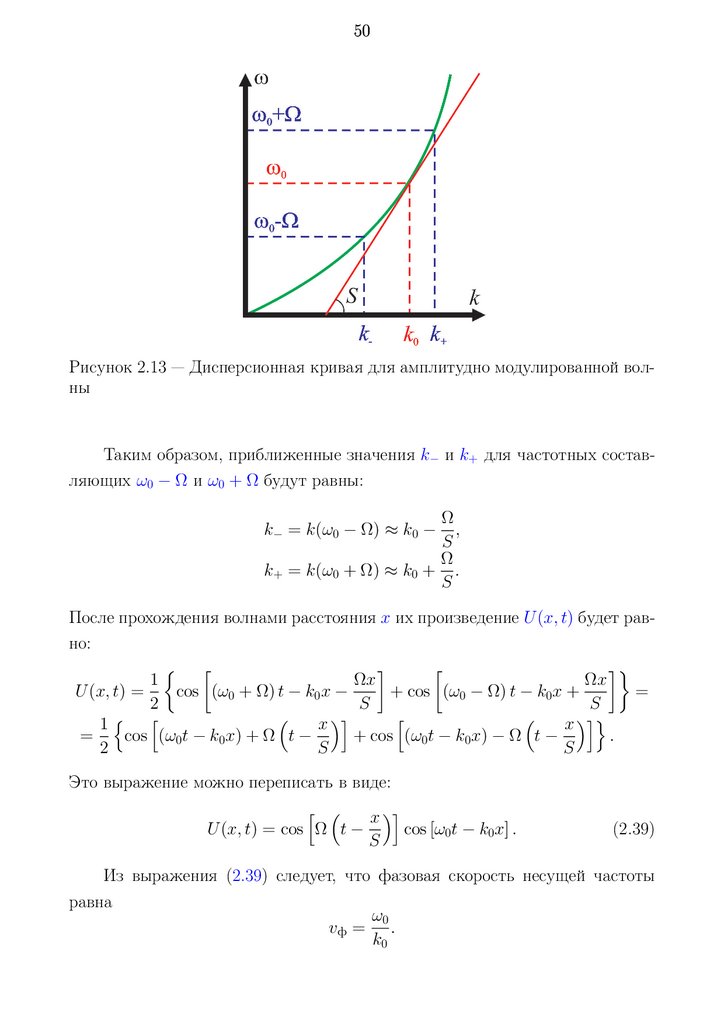




































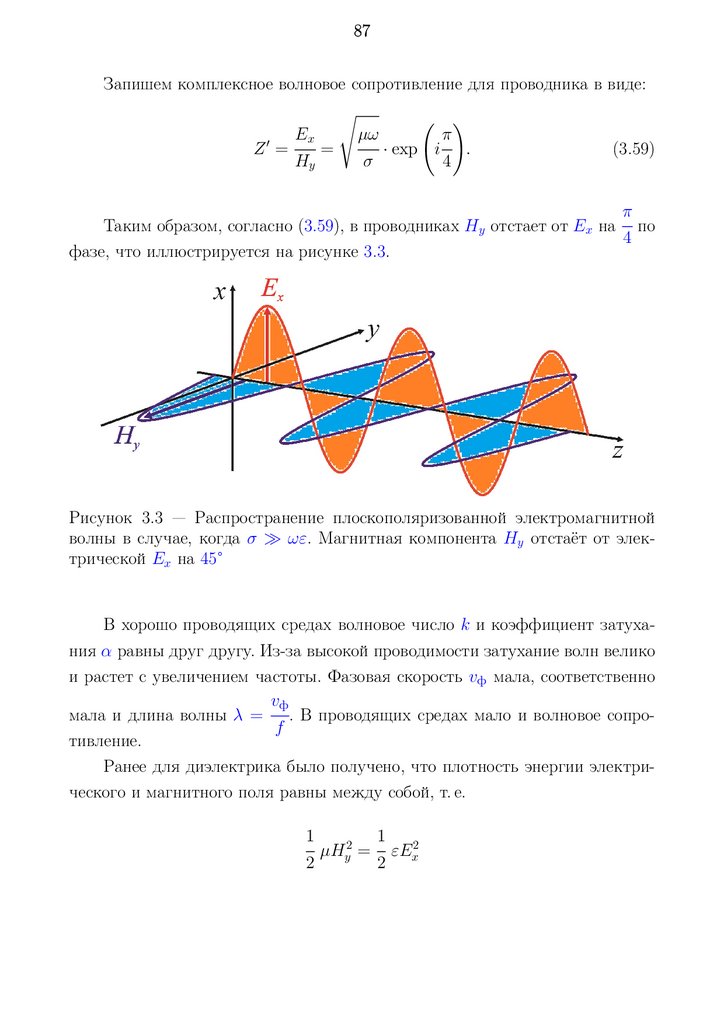














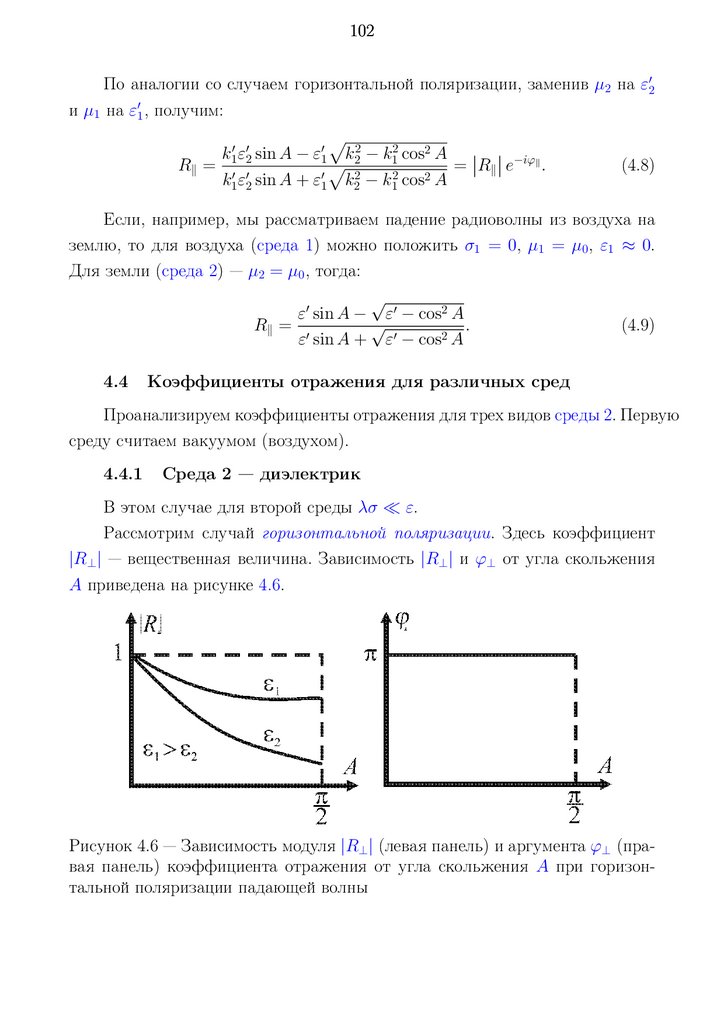


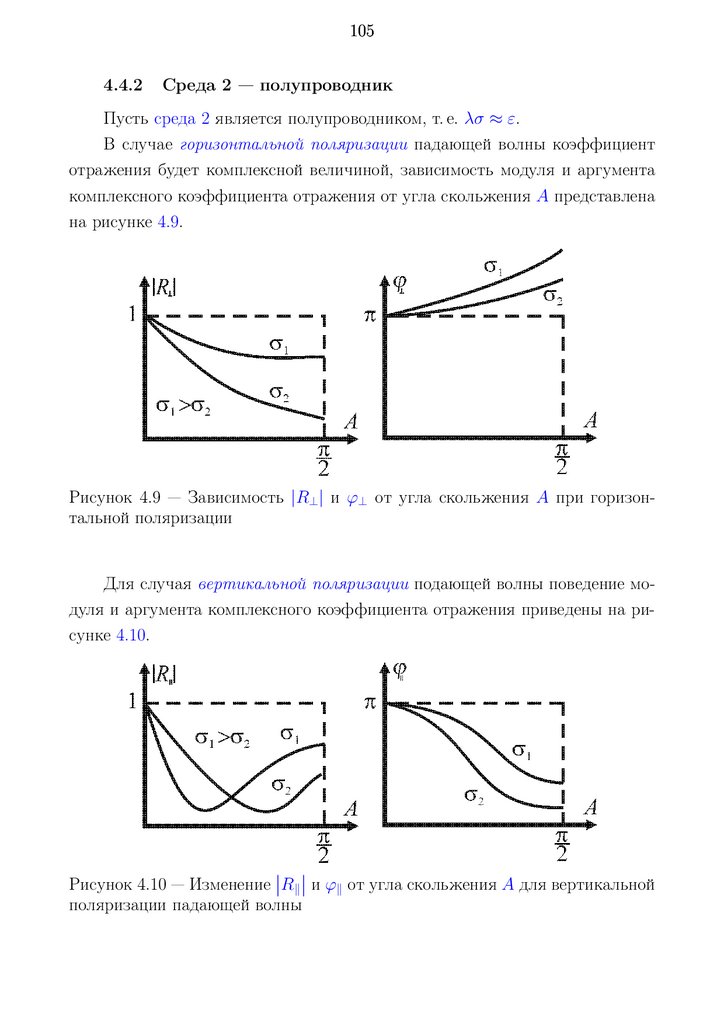



















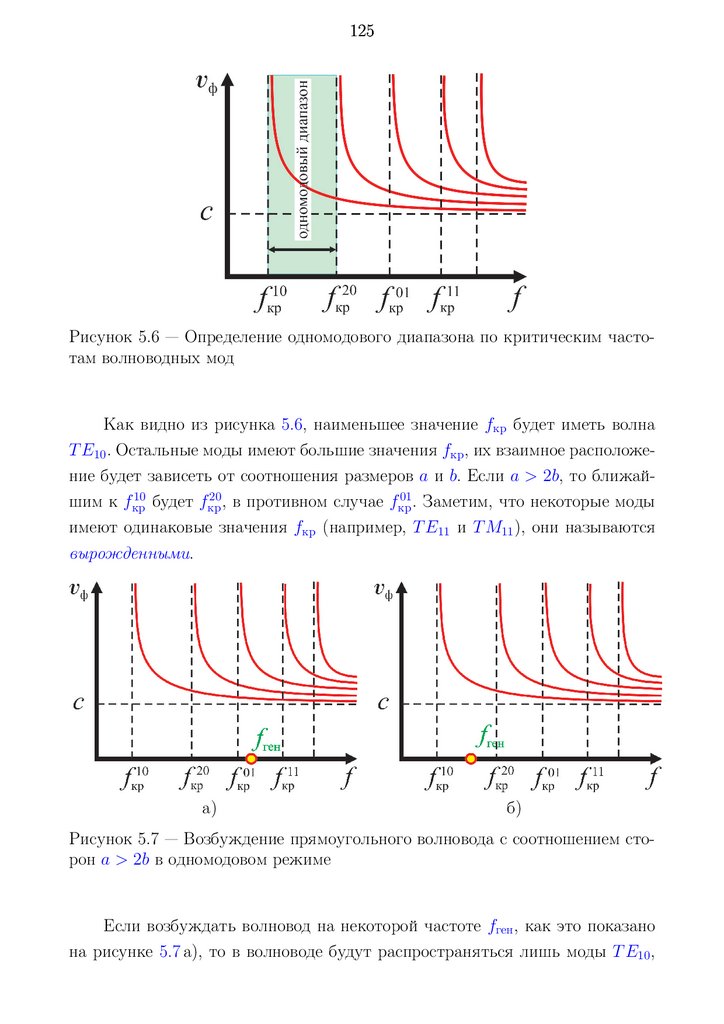











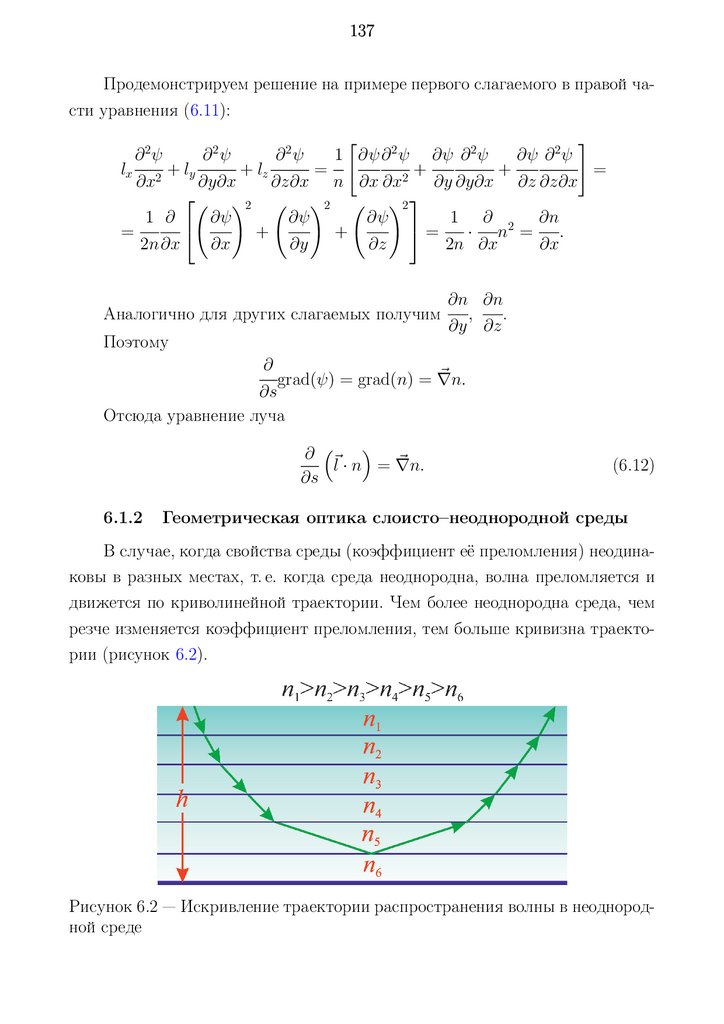


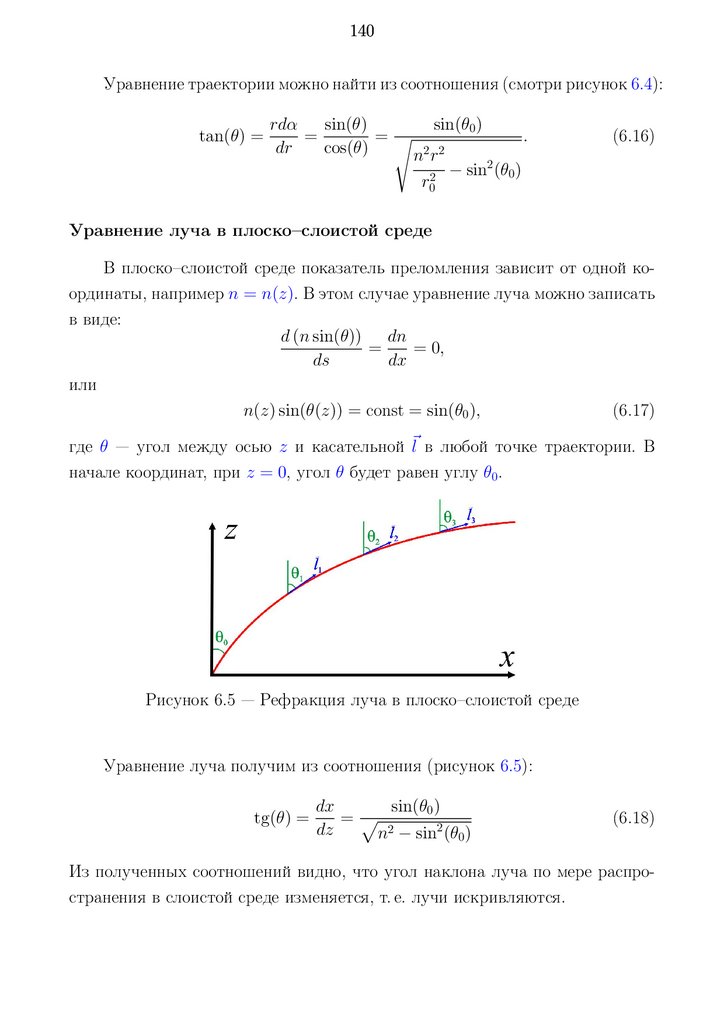
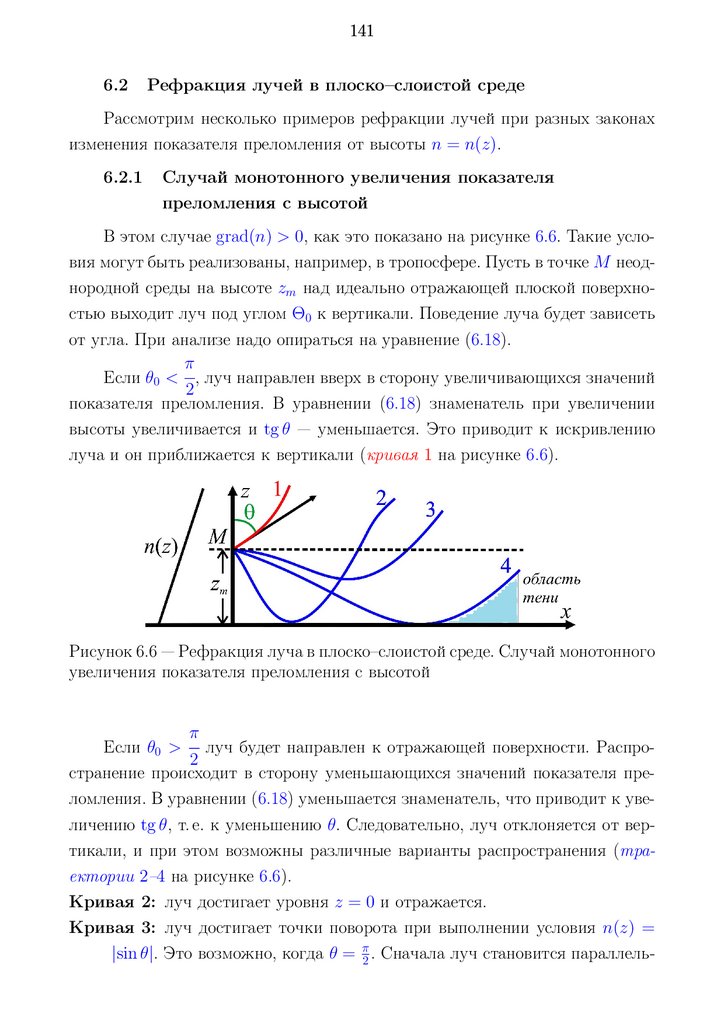
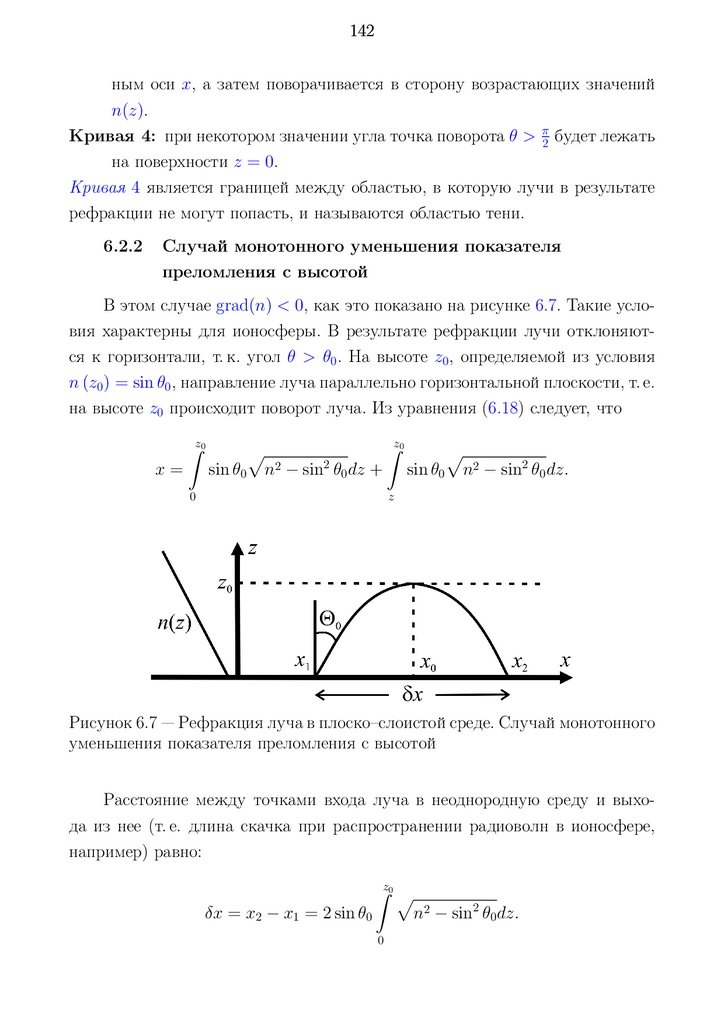



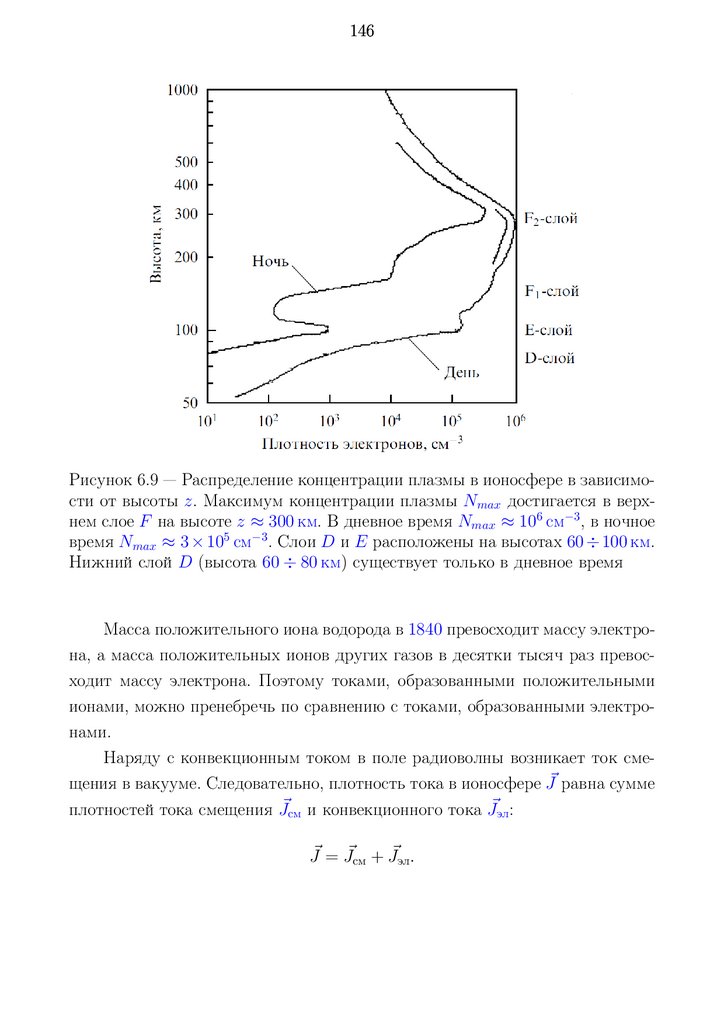













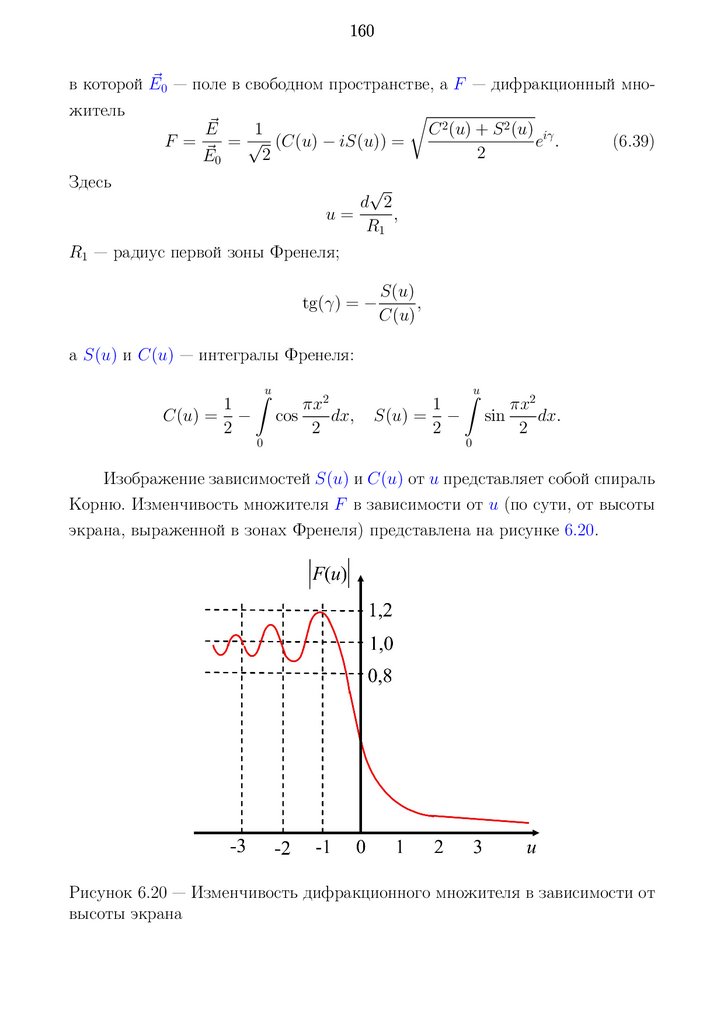



 Физика
Физика








