Похожие презентации:
Комбинаторика. Комбинаторные задачи
1.
2.
КомбинаторикаКомбинаторные задачи
3.
Комбинаторика – раздел математики, вкотором изучаются вопросы о том,
сколько различных комбинаций,
подчинённых тем или иным условиям,
можно составить из заданных объектов.
Решить комбинаторную задачу –
это значит выписать все возможные
комбинации, составленные из чисел,
слов, предметов и др., отвечающих
условию задачи.
4.
Методы решениякомбинаторных задач:
1.Метод перебора ;
2.Табличный метод (все условия вносятся в
таблицу, в ней же выполняется решение);
3.Построение дерева возможных вариантов
решений;
4.Построение граф - схемы.
5.
Для своих двух книг Машакупила три разные обложки.
Сколькими различными
способами она может обернуть
книги купленными обложками?
6.
Метод перебора• Обозначим книги М и Р
Обложки 1, 2,3
М1;
М2;
М3;
Р1;
Р2;
Р3;
7.
В школьной столовойприготовили на завтрак плов ,
кашу , блины , а из напитков сок , чай и молоко . Сколько
различных вариантов
завтрака можно составить?
8.
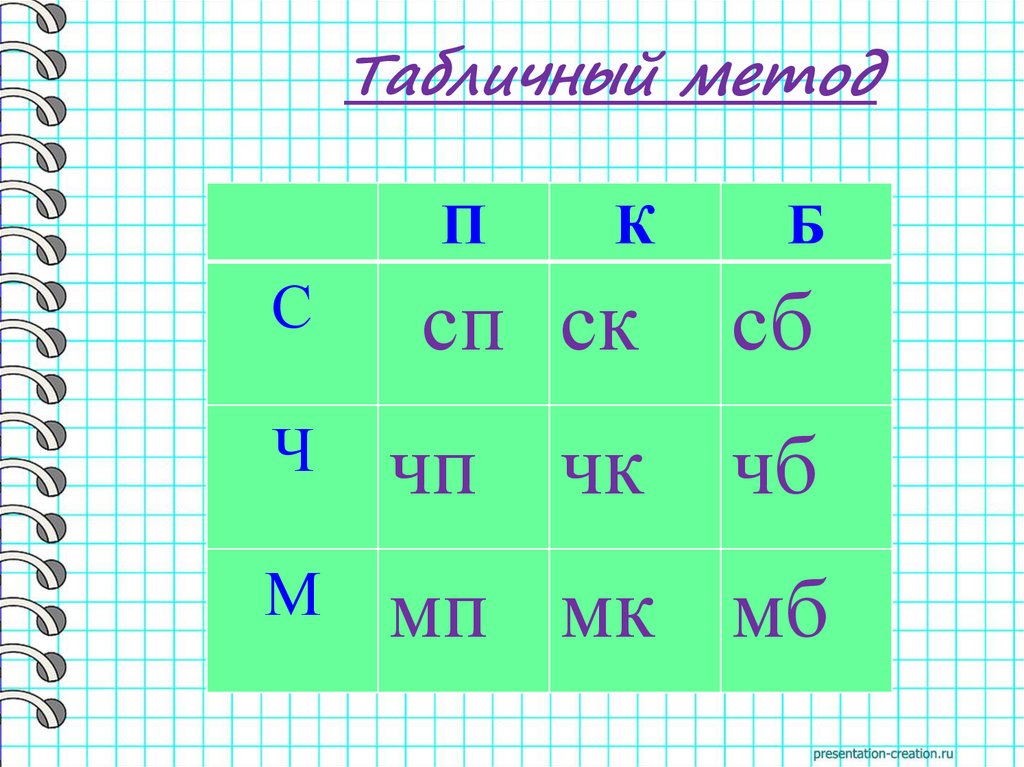
Табличный методП
К
Б
С
сп ск
сб
Ч
чп чк
чб
М
мп мк мб
9.
Катя собирается на выходные. Она может провестиих с сестрой или с родителями. Если Катя поедет с
сестрой, то она сможет провести выходные или на
катке, или в парке, или концерте. Если она поедет с
родителями, то она сможет провести выходные или
посещая театр, или на выставке, или в музее.
Сколько разных вариантов есть у Кати, чтобы
провести свои каникулы?
10.
Выходныесестра
каток
парк
концерт
родители
театр
музей
выставка
Построение дерева возможных вариантов
11.
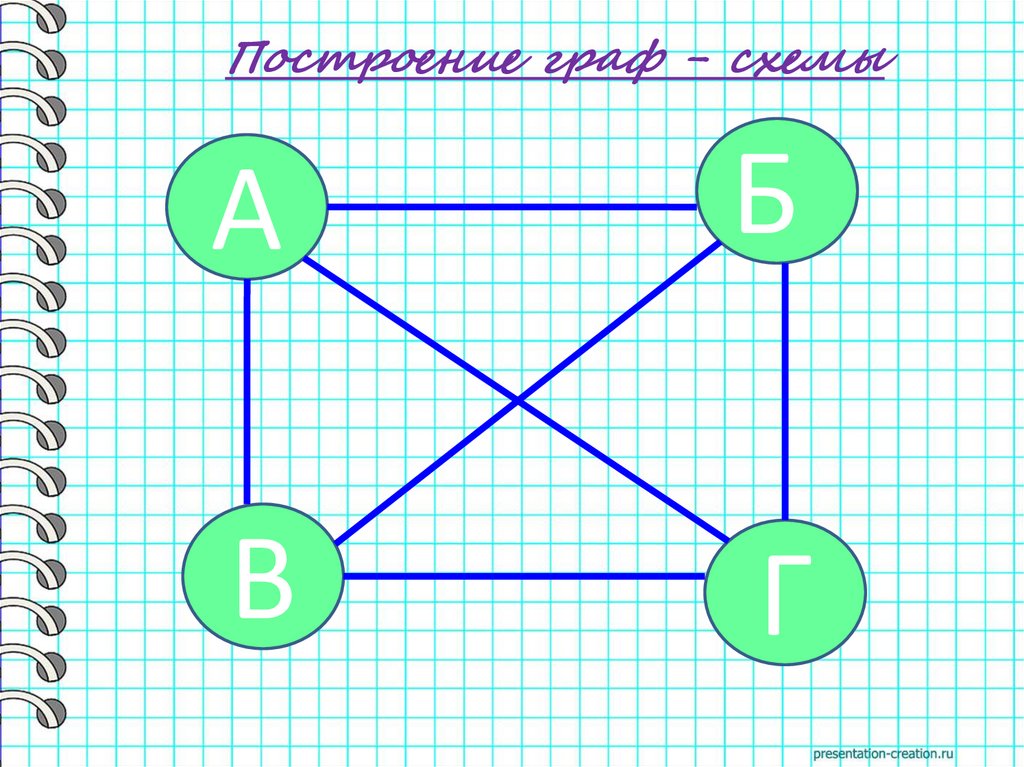
Аня, Борис, Вика и Григорийиграли в шахматы. Каждый сыграл
с каждым по одной партии.
Сколько партий было сыграно?
12.
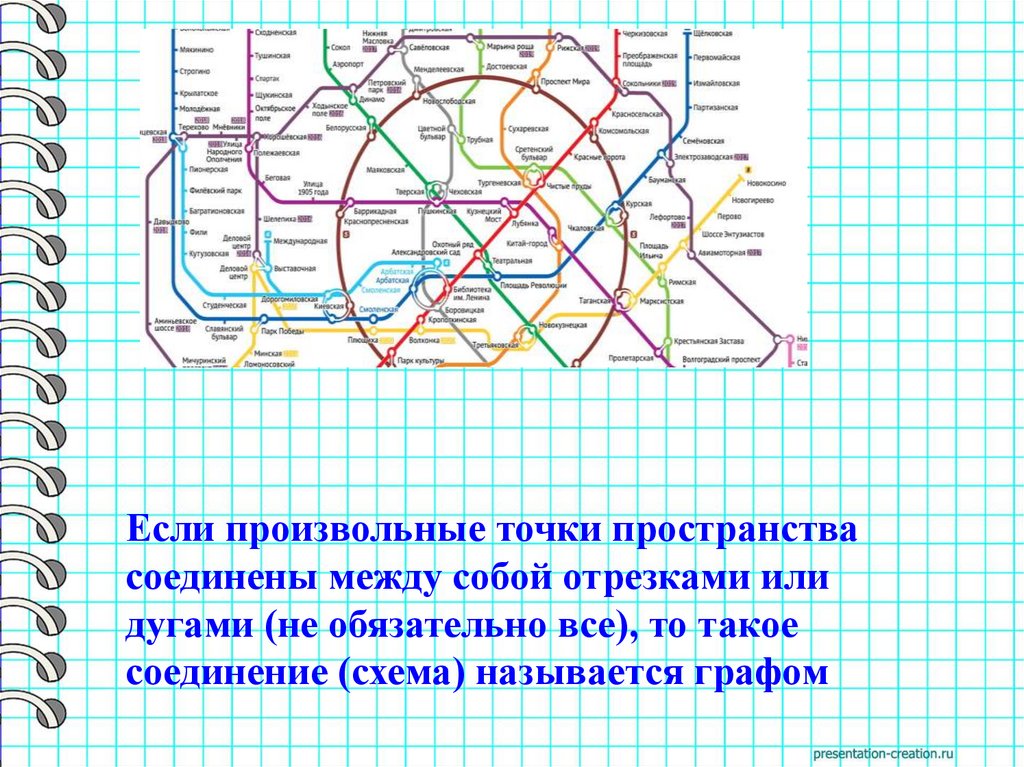
Если произвольные точки пространствасоединены между собой отрезками или
дугами (не обязательно все), то такое
соединение (схема) называется графом
13.
Граф - это геометрическая фигура,состоящая из точек (вершины графа) и
линий, их соединяющих (рёбра графа).
При этом с помощью вершин изображают
элементы некоторого множества
(предметов, людей и т.д.), а с помощью
рёбер - определённые связи между
элементами. Для удобства иллюстрации
условия задачи, вершины графа могут быть
заменены кругами или прямоугольниками
14.
Построение граф - схемыА
Б
В
Г
15.
Флаг Российской Федерации16.
Дерево вариантов17.
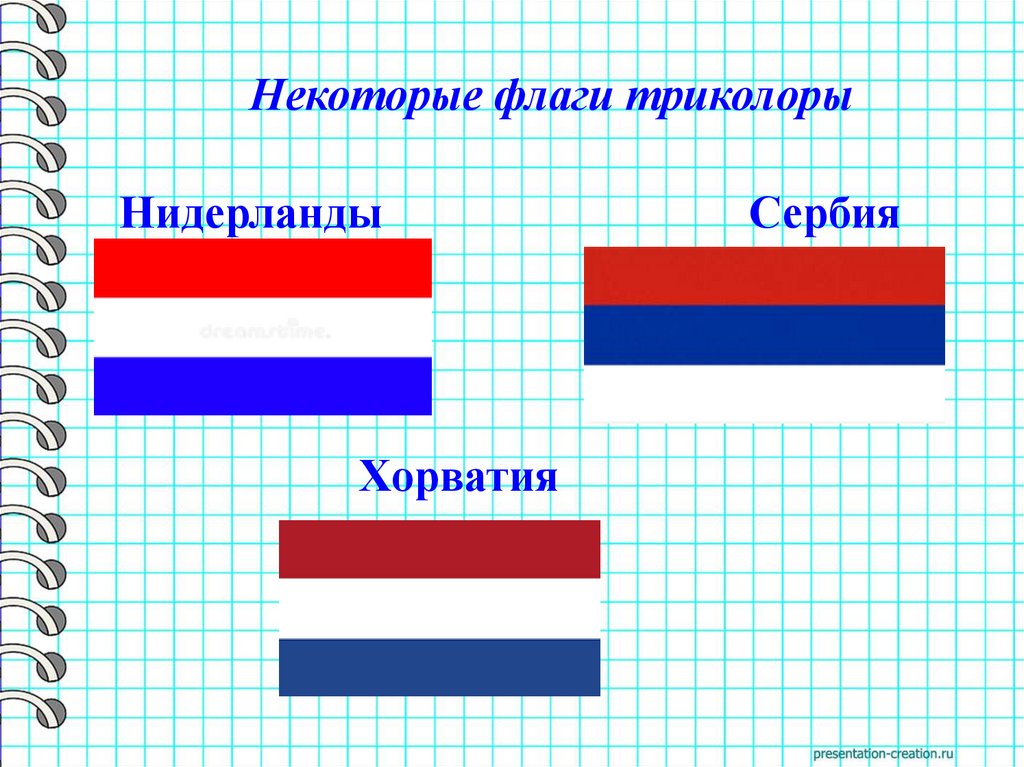
Некоторые флаги триколорыНидерланды
Хорватия
Сербия
18.
Работаем с учебником№844 №846
19.
№844 Метод построение деревавозможных вариантов решений
• 1.
Витя
• 2 Толя Игорь
Толя
Игорь Витя
Игорь
Толя
Витя
• 3. Игорь Толя
Витя
Игорь
Витя Толя
Два варианта очереди – Игорь на первом месте
Четыре варианта-Витя не на последнем
20.
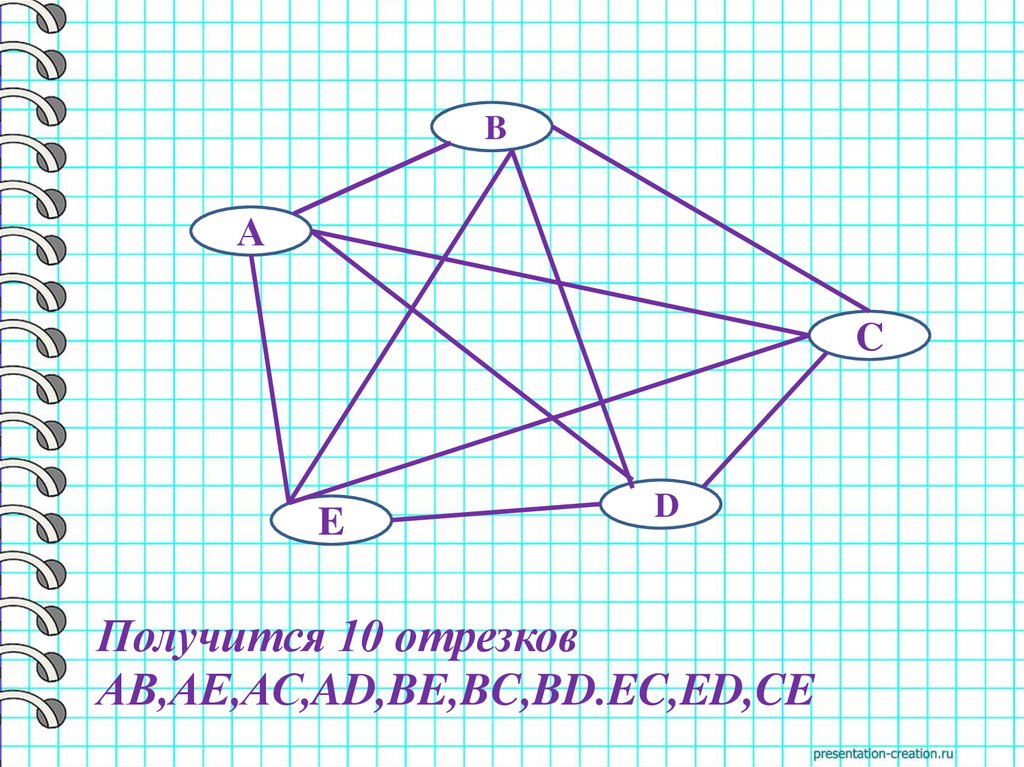
BBаА
C
E
аD
Получится 10 отрезков
АВ,АЕ,АС,AD,BE,BC,BD.EC,ED,CE















 Математика
Математика








