Пропорциональные отрезки. 8 класс

1.

2.

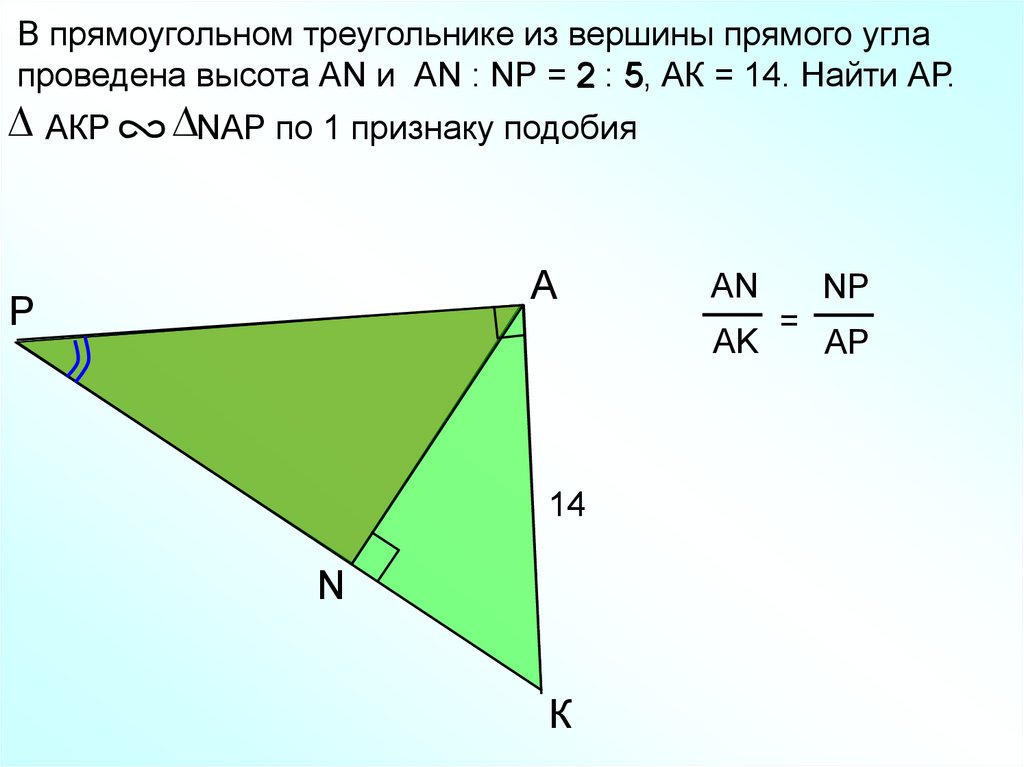
В прямоугольном треугольнике из вершины прямого угла
проведена высота АN и АN : NP = 2
2 : 5,
5 АК = 14. Найти АР.
AКР
NAP по 1 признаку подобия
A
P
AN
AK
14
N
К
NP
=
AP

3.

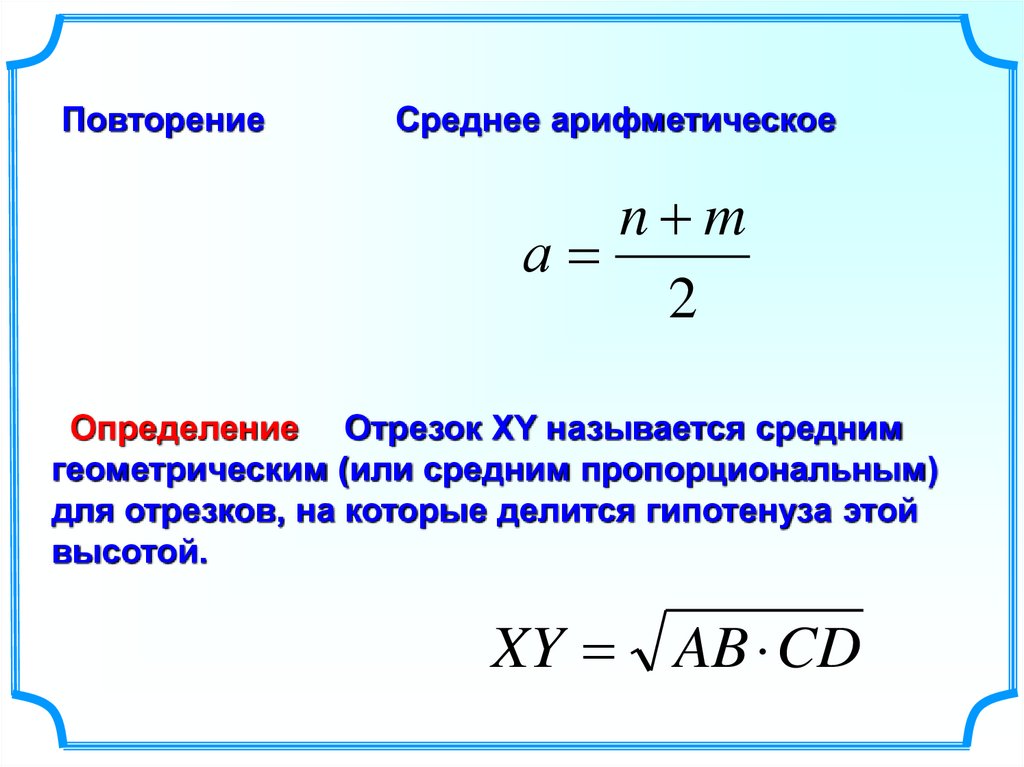
Повторение
Среднее арифметическое
n m
а
2
Определение Отрезок XY называется средним
геометрическим (или средним пропорциональным)
для отрезков, на которые делится гипотенуза этой
высотой.
XY AB CD

4.

c
C
bc
ac
h
a
A
D
B
b

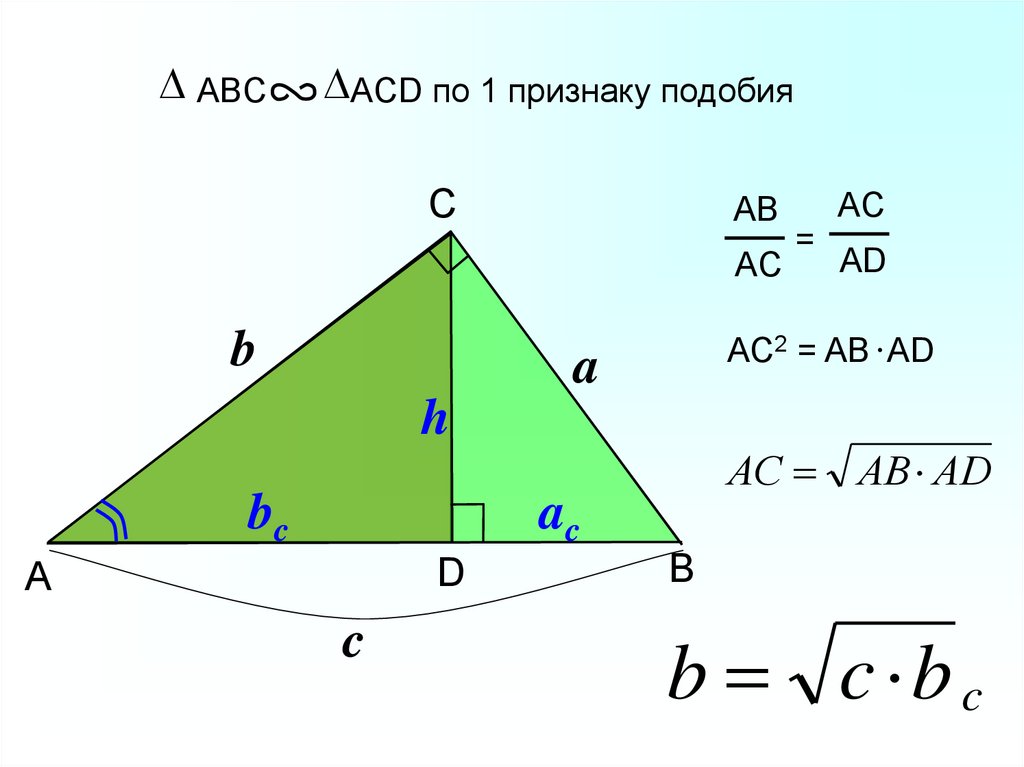
5.

ABC
ACD по 1 признаку подобия
C
AB
AC
b
h
D
c
AD
АС АВ АD
ac
A
=
AC2 = AB AD
a
bc
AC
B
b c b c

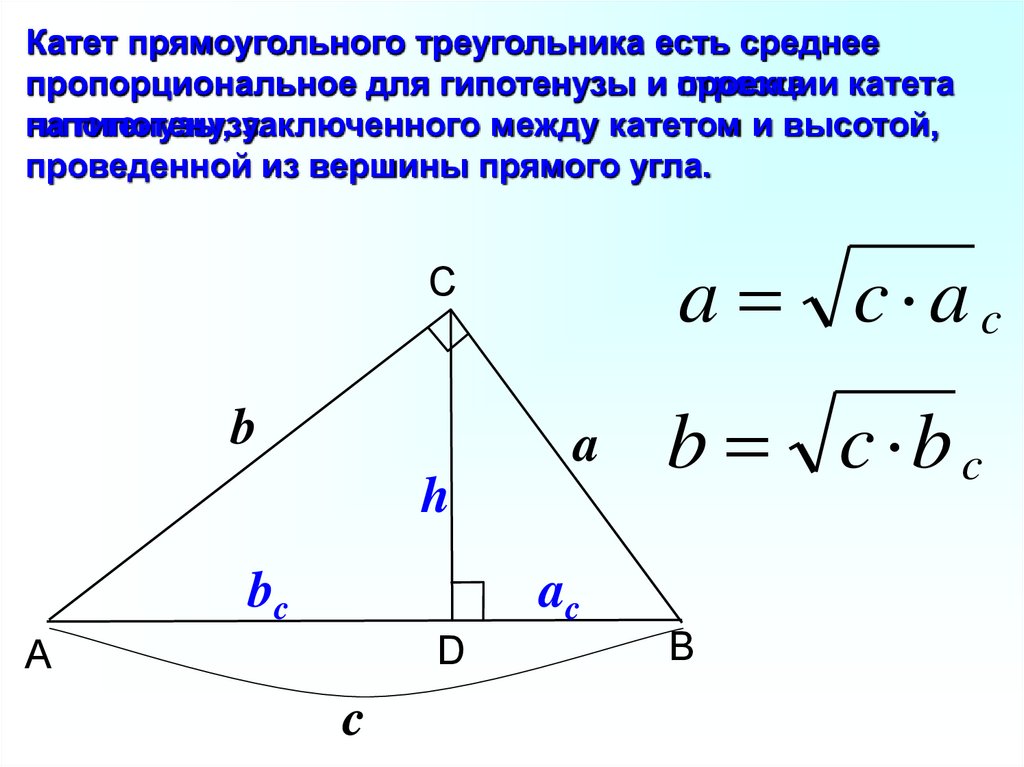
6.

Катет прямоугольного треугольника есть среднее
пропорциональное для гипотенузы и проекции
отрезка катета
гипотенузы,
на
гипотенузу.
заключенного между катетом и высотой,
проведенной из вершины прямого угла.
a c ac
C
b
a
h
bc
b c b c
ac
D
A
c
B

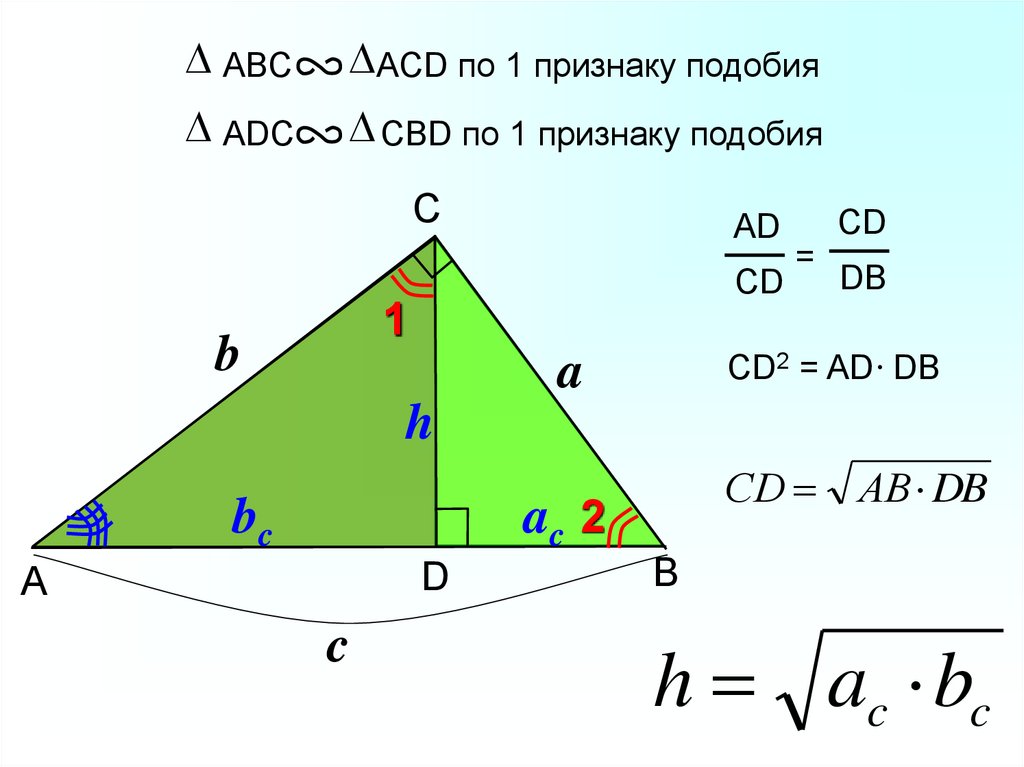
7.

ABC
ACD по 1 признаку подобия
ADC
CBD по 1 признаку подобия
C
AD
CD
1
b
CD
=
DB
CD2 = AD DB
a
h
bc
СD АВ DB
ac 2
D
A
c
B
h ac bc

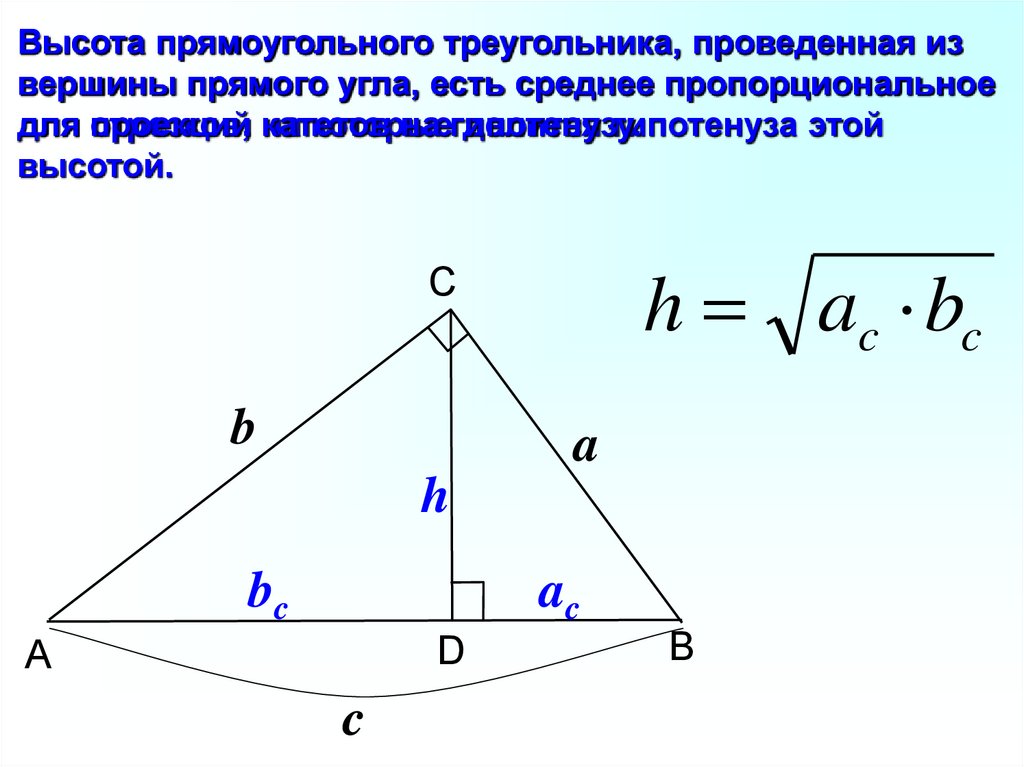
8.

Высота прямоугольного треугольника, проведенная из
вершины прямого угла, есть среднее пропорциональное
для проекций
отрезков, на
катетов
которые
на гипотенузу.
делится гипотенуза этой
высотой.
h ac bc
C
b
a
h
bc
ac
D
A
c
B

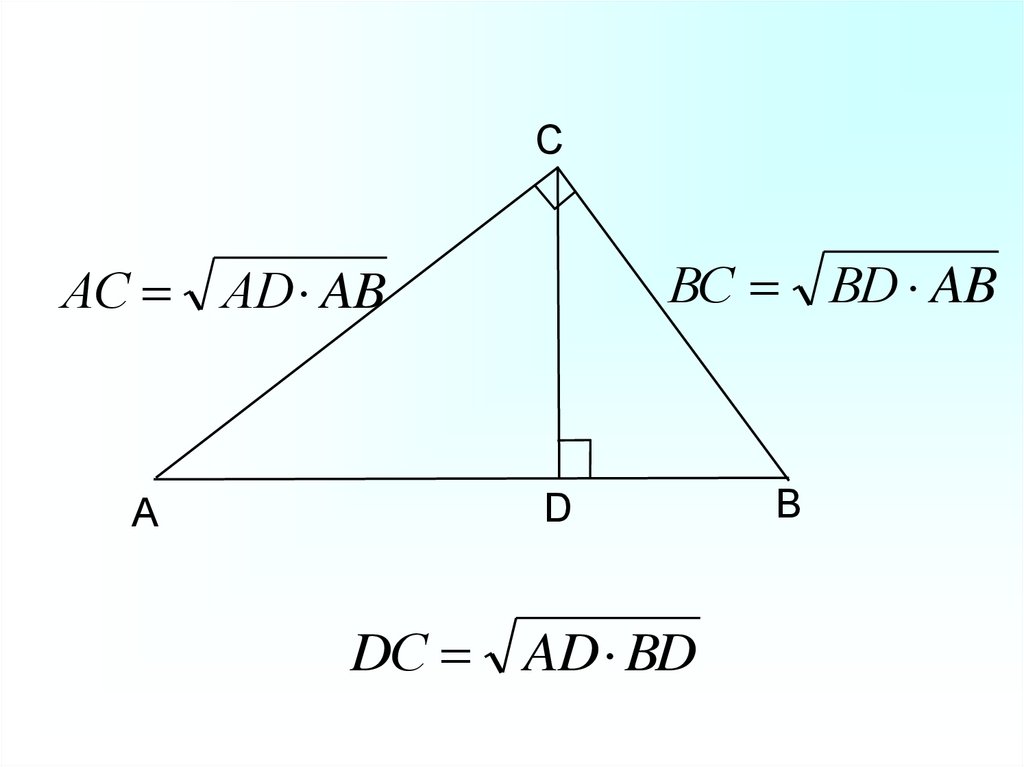
9.

C
ВС ВD AB
АС АD AB
А
D
DС AD BD
B

10.

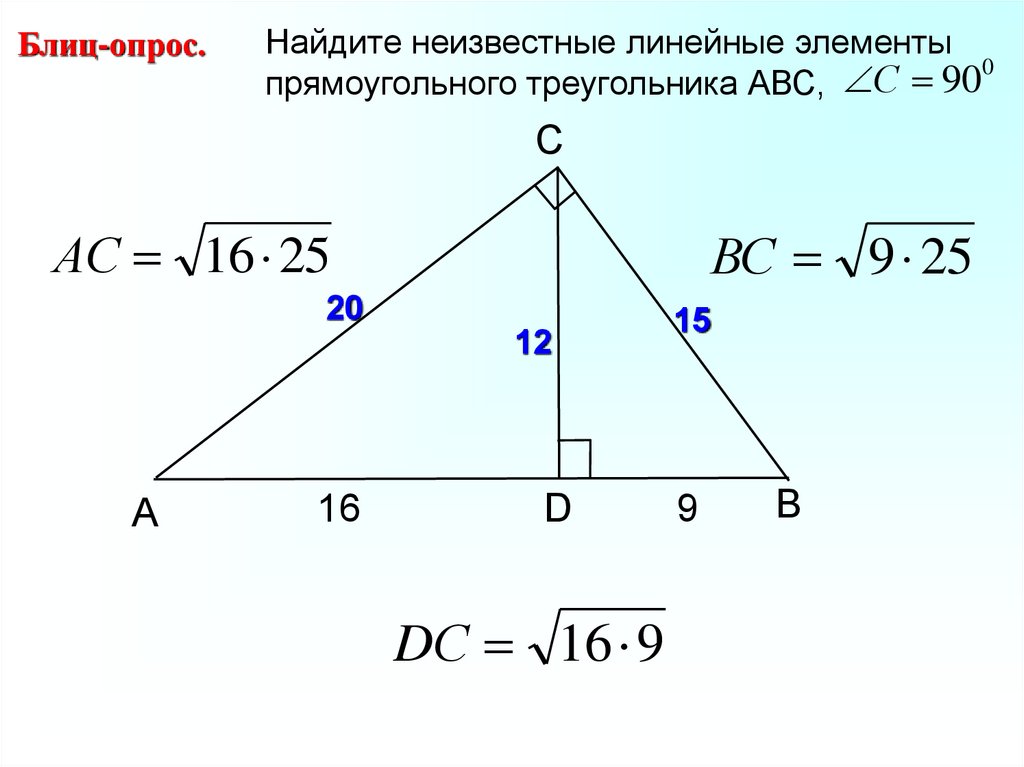
Блиц-опрос.
Найдите неизвестные линейные элементы
0
прямоугольного треугольника АВС, С 90
C
АС 16 25
ВС 9 25
20
12
А
16
D
DС 16 9
15
9
B

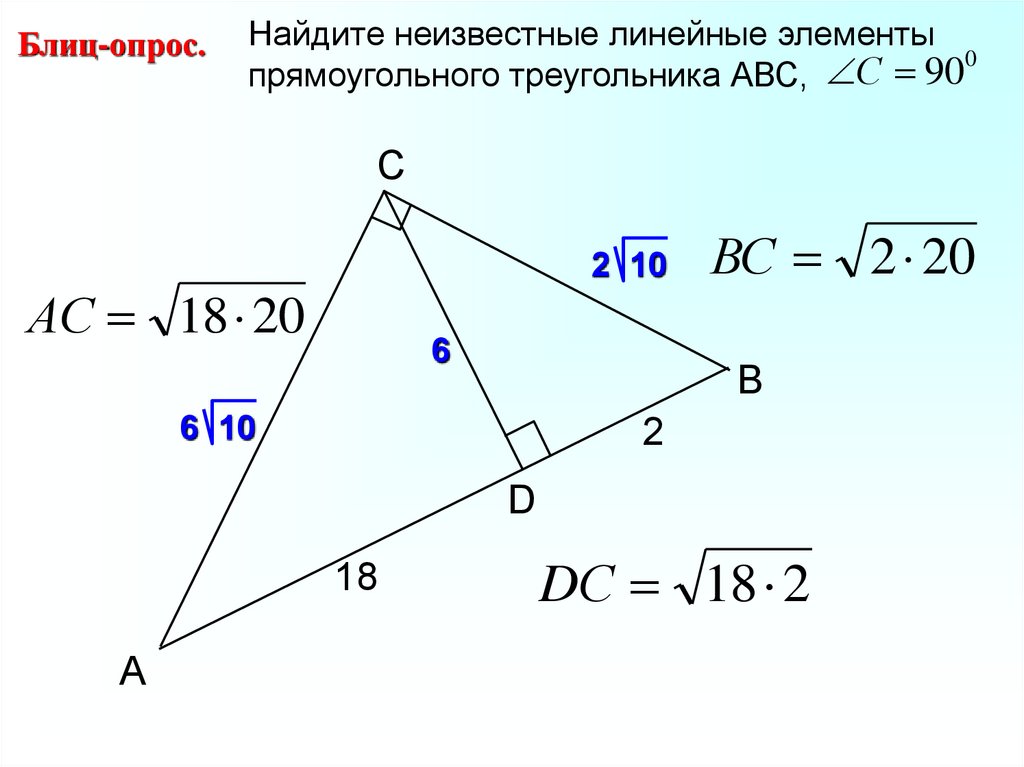
11.

Блиц-опрос.
Найдите неизвестные линейные элементы
0
С
90
прямоугольного треугольника АВС,
C
2 10
АС 18 20
6
ВС 2 20
B
6 10
2
D
18
А
DС 18 2

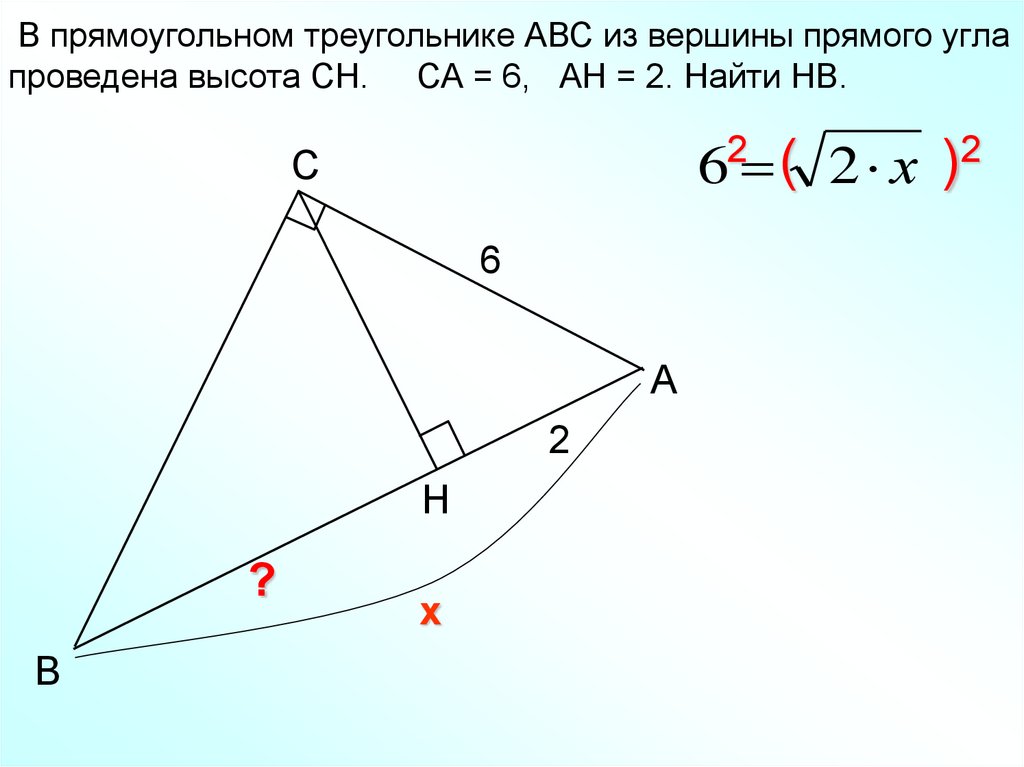
12.

В прямоугольном треугольнике АВС из вершины прямого угла
проведена высота СН. СА = 6, АН = 2. Найти НВ.
2
(
)
6 2 х
2
C
6
А
2
Н
?
В
х

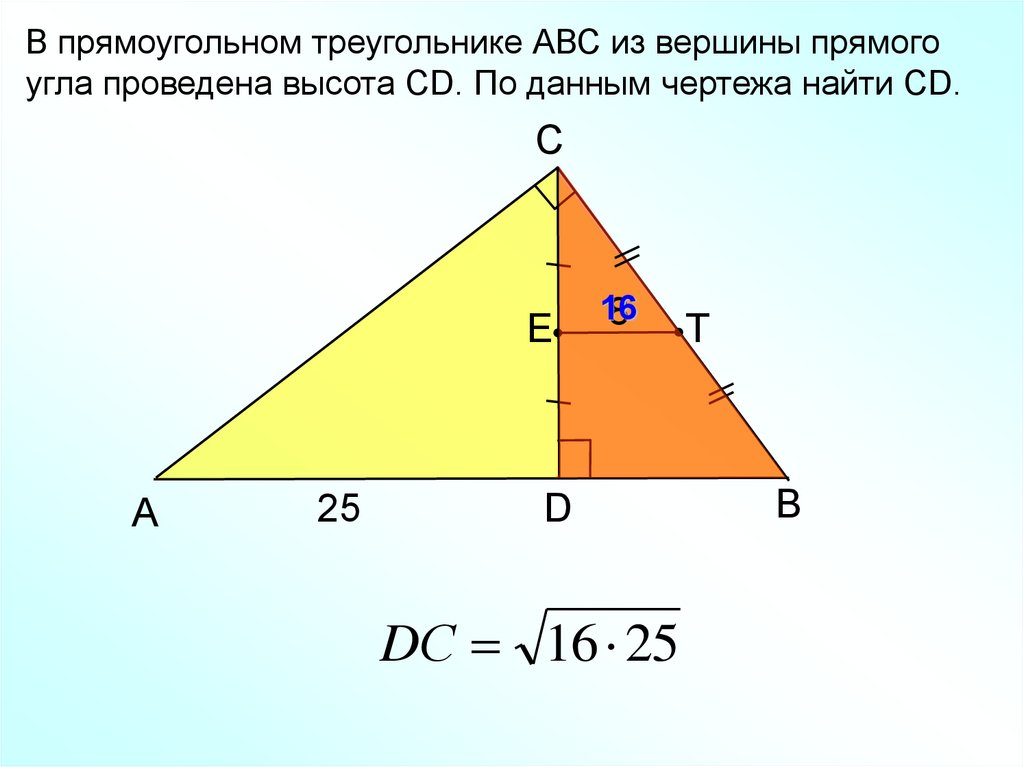
13.

В прямоугольном треугольнике АВС из вершины прямого
угла проведена высота СD. По данным чертежа найти СD.
C
Е
А
25
16
8
D
DС 16 25
Т
B

14.

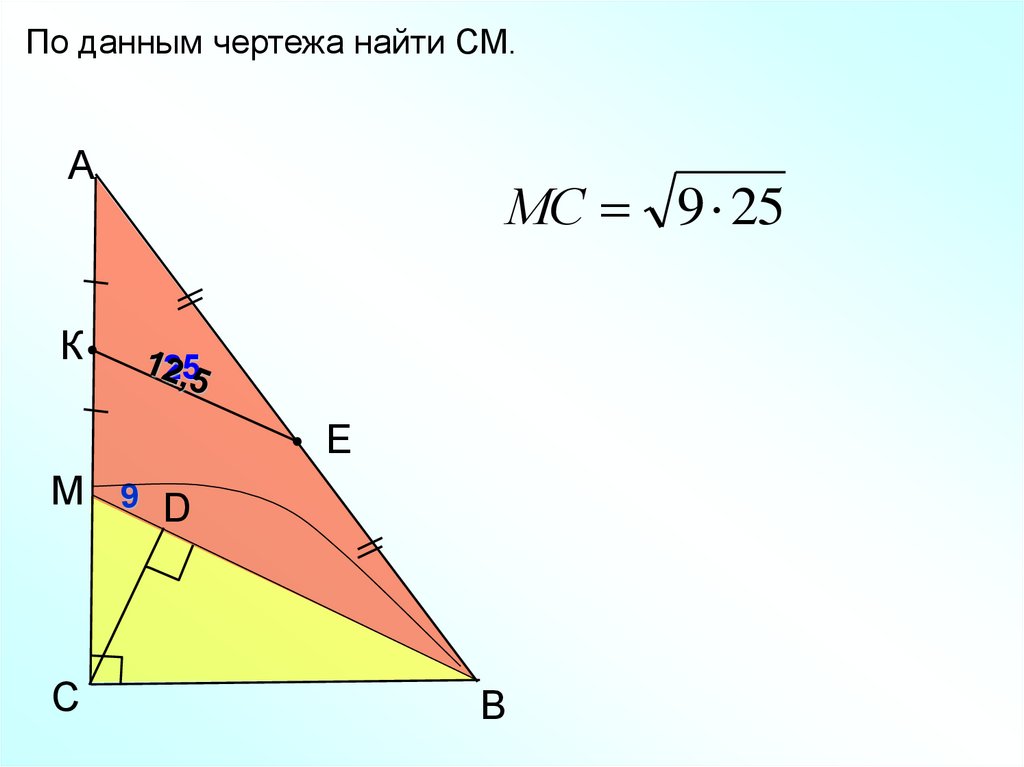
По данным чертежа найти СМ.
А
К
МС 9 25
25
Е
М 9 D
C
B

15.

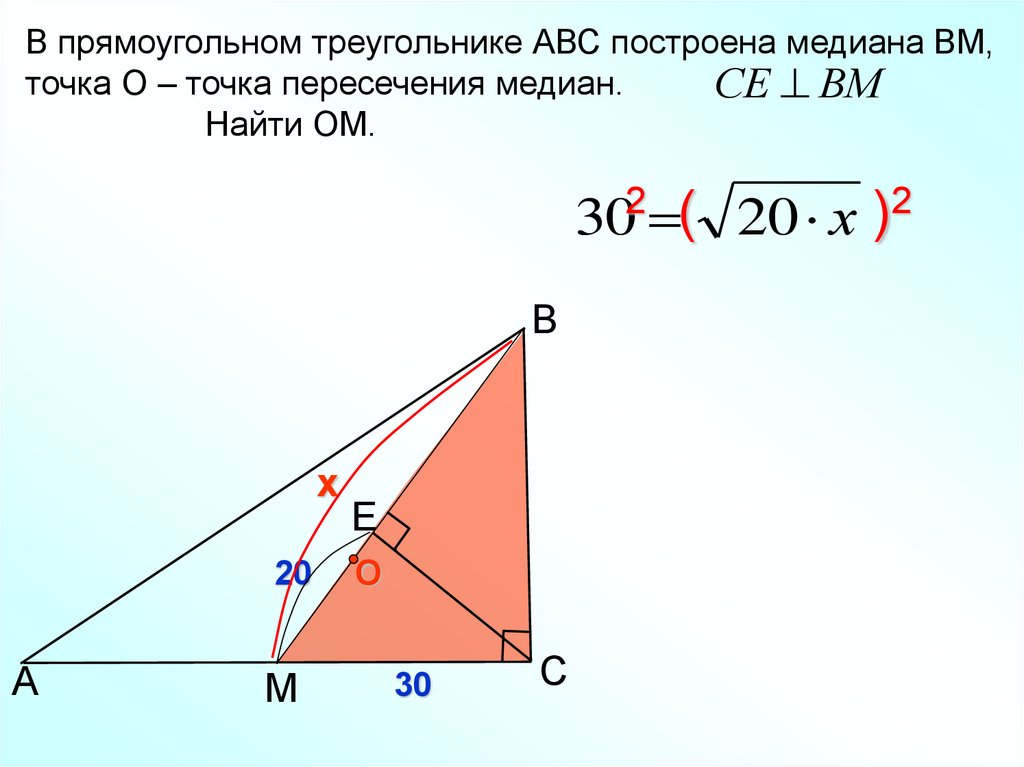
В прямоугольном треугольнике АВС построена медиана ВМ,
точка О – точка пересечения медиан.
СЕ ВМ
Найти ОМ.
2
(
)
30 20 х
2
B
х
20
А
М
Е
О
30
C

16.

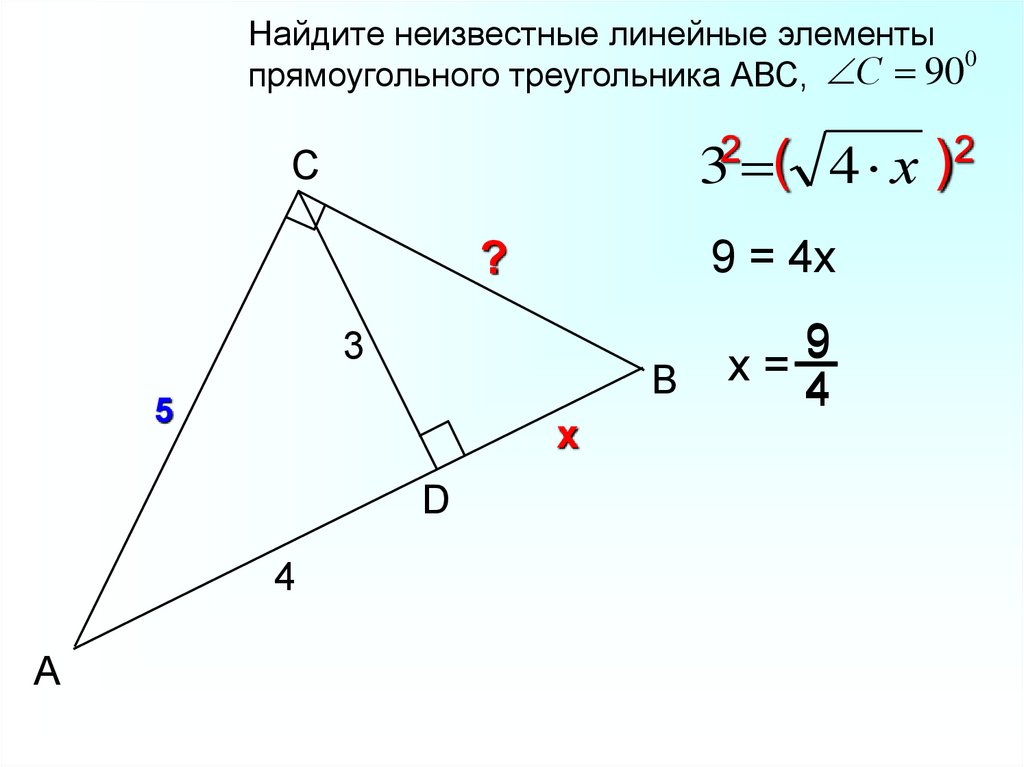
Найдите неизвестные линейные элементы
0
С
90
прямоугольного треугольника АВС,
2
(
)
3 4 х
2
C
9 = 4х
?
3
B
5
х
D
4
А
9
х=
4

17.

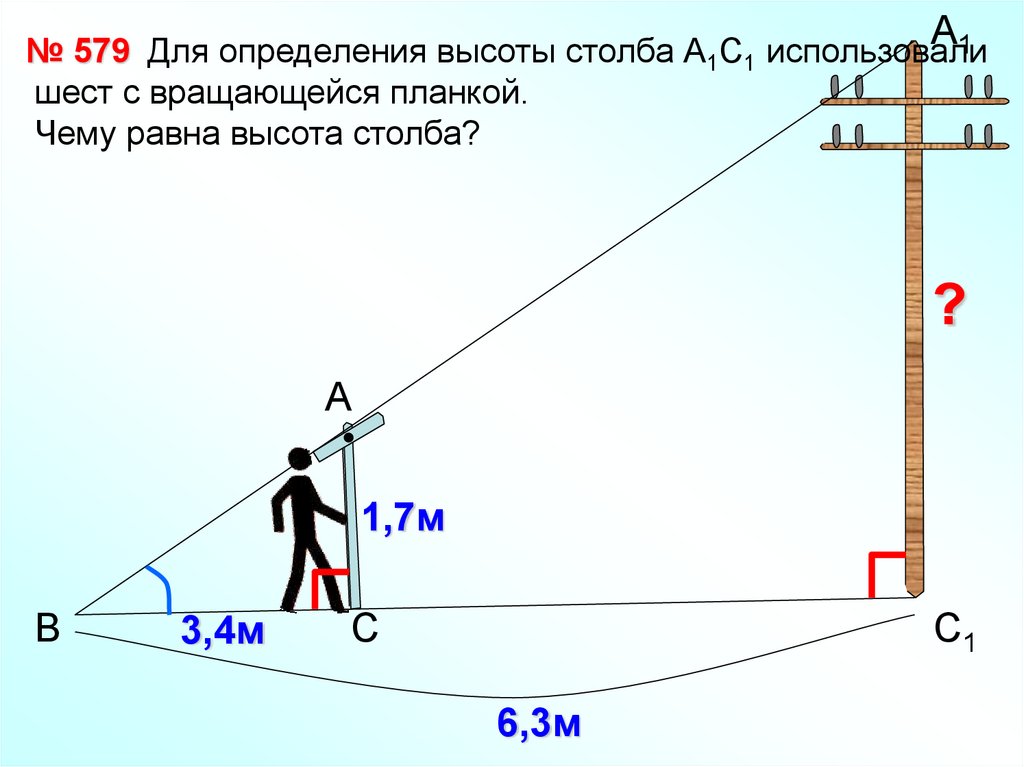
А
1
№ 579 Для определения высоты столба А С использовали
шест с вращающейся планкой.
Чему равна высота столба?
1
1
?
А
1,7м
В
3,4м
С
С1
6,3м

18.

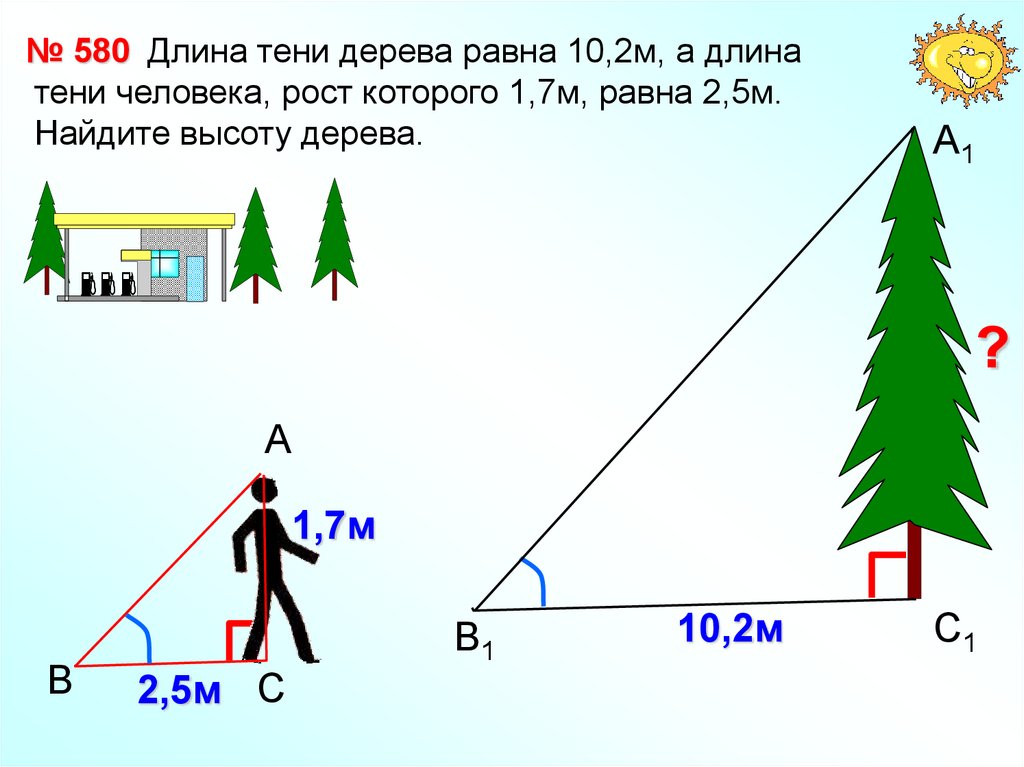
№ 580 Длина тени дерева равна 10,2м, а длина
тени человека, рост которого 1,7м, равна 2,5м.
Найдите высоту дерева.
А1
?
А
1,7м
В
В1
2,5м С
10,2м
С1

19.

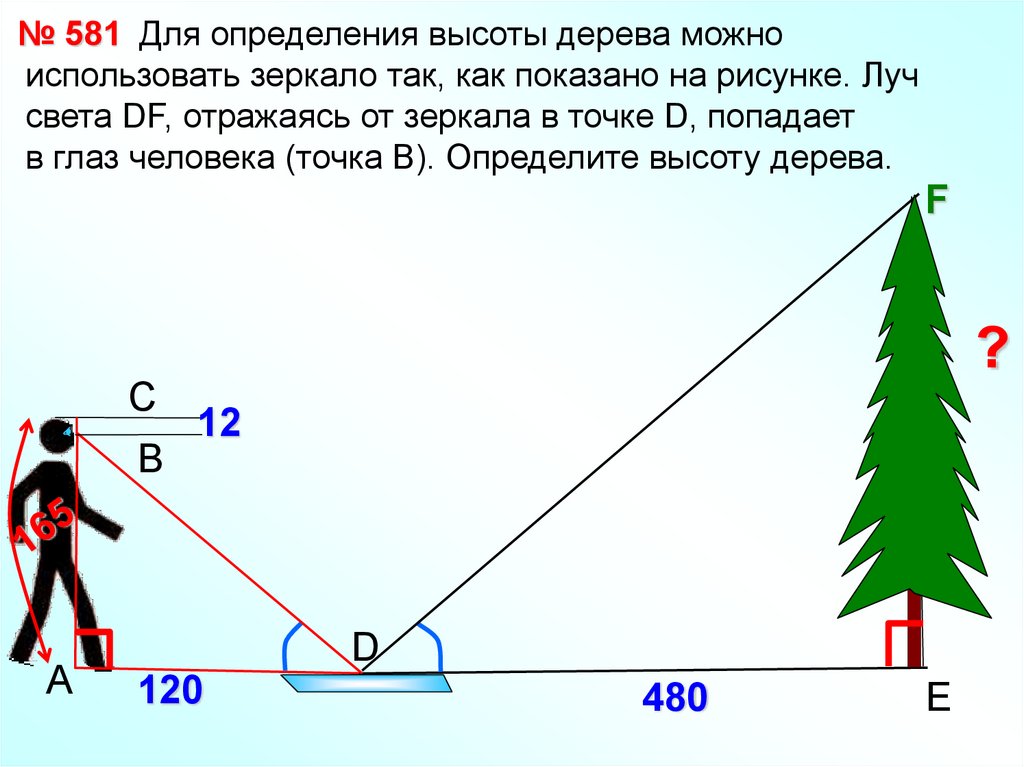
№ 581 Для определения высоты дерева можно
использовать зеркало так, как показано на рисунке. Луч
света DF, отражаясь от зеркала в точке D, попадает
в глаз человека (точка В). Определите высоту дерева.
F
С
B
А
?
12
D
120
480
E

20.

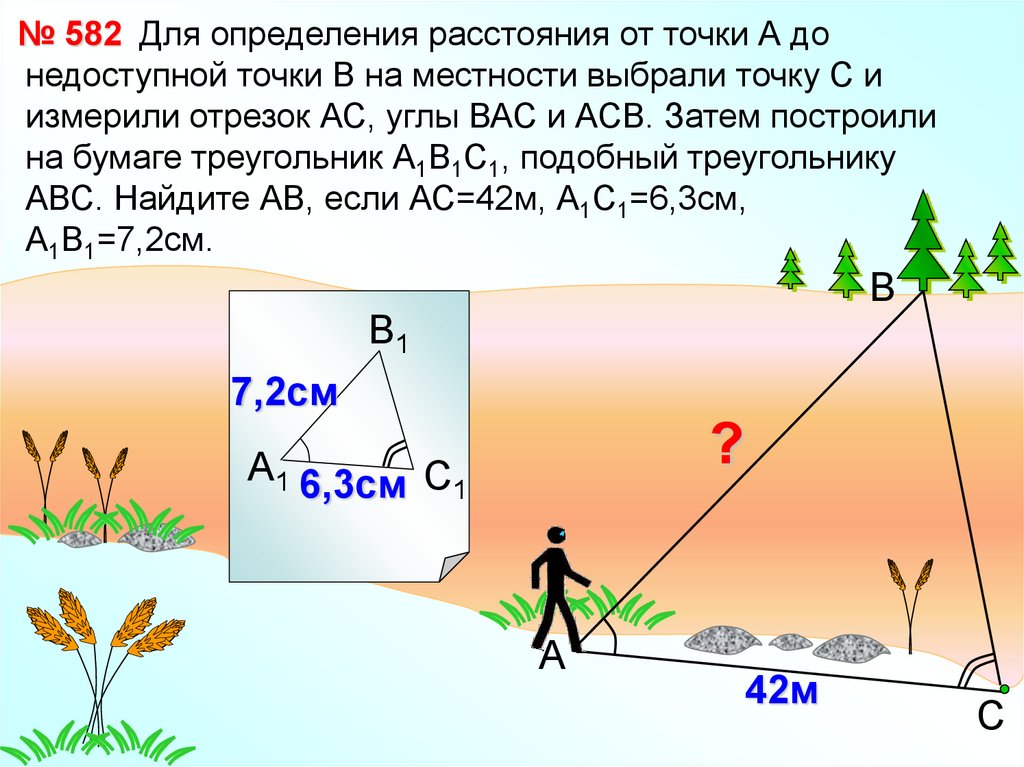
№ 582 Для определения расстояния от точки А до
недоступной точки В на местности выбрали точку С и
измерили отрезок АС, углы ВАС и АСВ. Затем построили
на бумаге треугольник А1В1С1, подобный треугольнику
АВС. Найдите АВ, если АС=42м, А1С1=6,3см,
А1В1=7,2см.
В
В1
7,2см
?
А1 6,3см С1
А
42м
С

21.

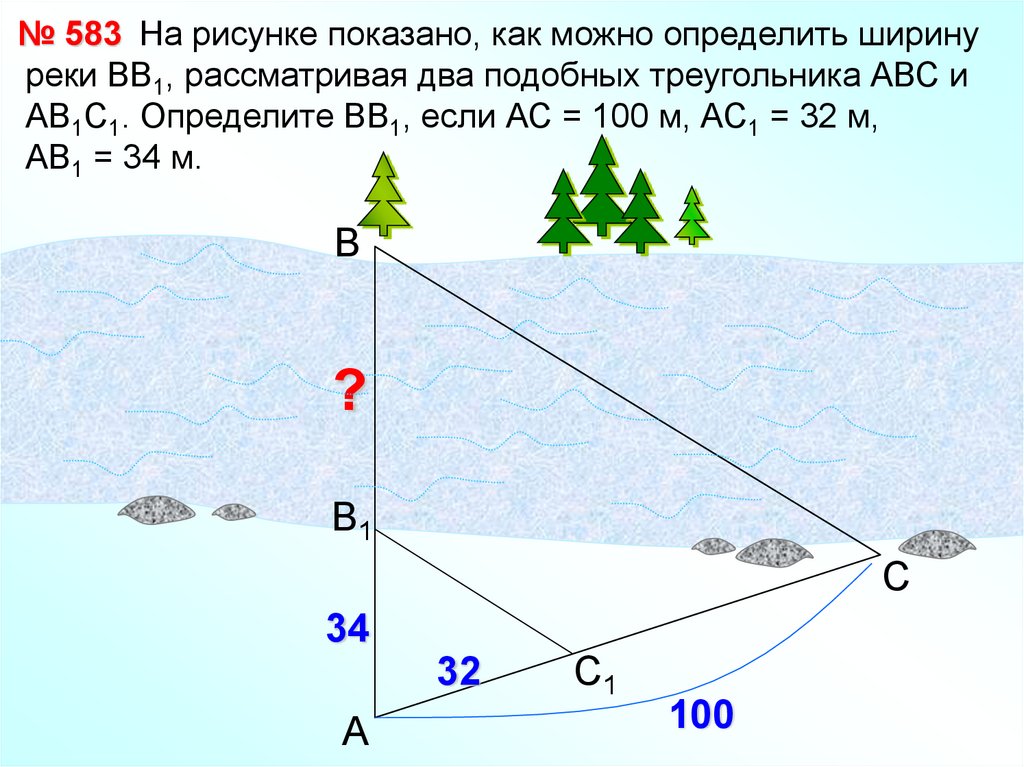
№ 583 На рисунке показано, как можно определить ширину
реки ВВ1, рассматривая два подобных треугольника АВС и
АВ1С1. Определите ВВ1, если АС = 100 м, АС1 = 32 м,
АВ1 = 34 м.
В
?
В1
С
34
32
А
С1
100

22.

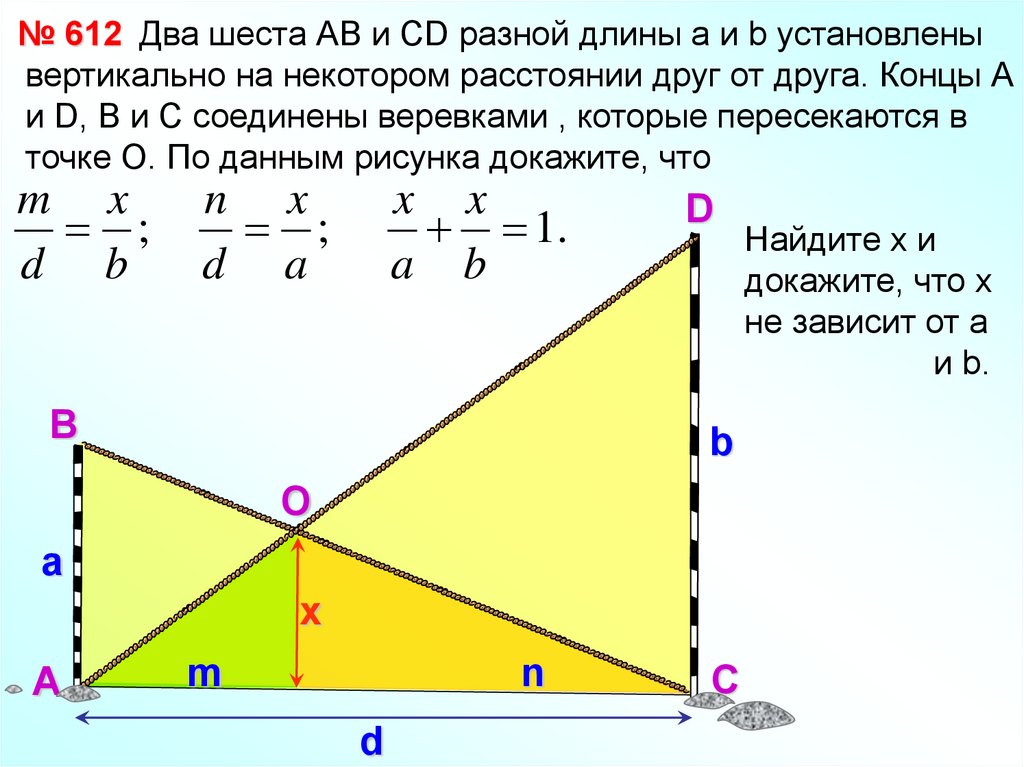
№ 612 Два шеста АВ и СD разной длины а и b установлены
вертикально на некотором расстоянии друг от друга. Концы А
и D, В и С соединены веревками , которые пересекаются в
точке О. По данным рисунка докажите, что
m x
;
d b
n x
;
d a
x x
1.
a b
B
D
b
O
a
x
А
m
n
d
С
Найдите х и
докажите, что х
не зависит от а
и b.