Похожие презентации:
Производная. Определение производной
1.
2. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Задачи, приводящие к понятиюпроизводной
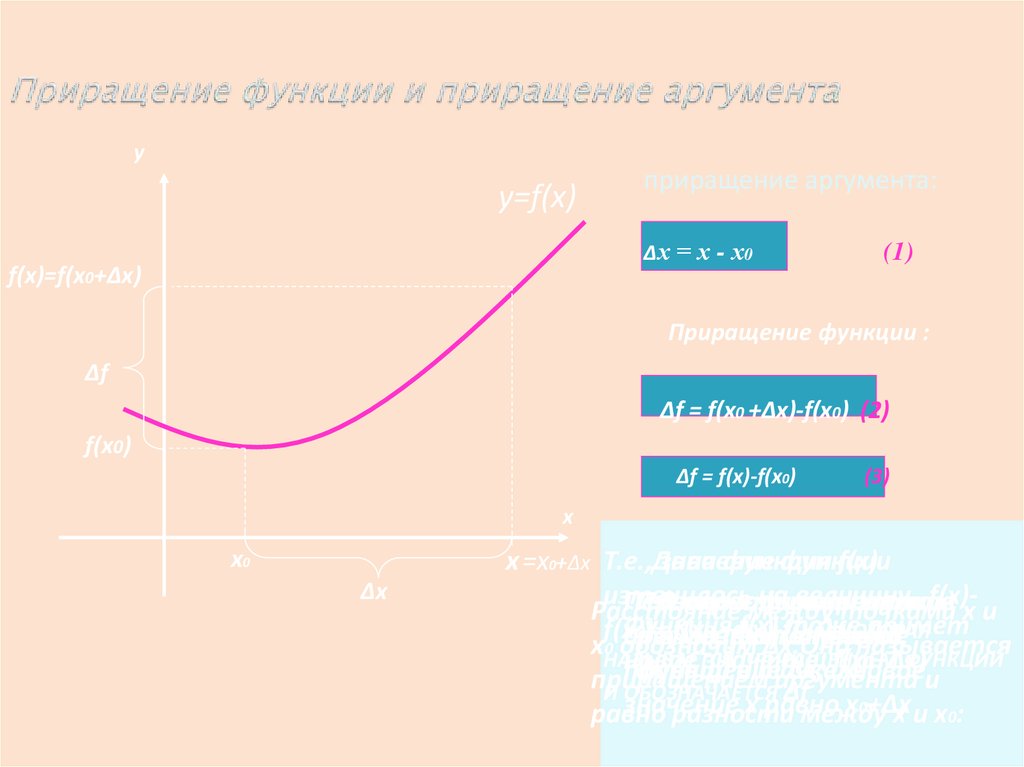
3. Приращение функции и приращение аргумента
yy=f(x)
приращение аргумента:
∆х = х - х0
f(x)=f(x0+∆x)
(1)
Приращение функции :
∆f
∆f = f(x0 +∆x)-f(x0) (2)
f(x0)
∆f = f(x)-f(x0)
(3)
x
x0
∆x
x =x0+∆x Т.е.,Дана
значение
функция
функции
f(x)
изменилось
на
величину
f(x)Первоначальное
Пусть
В окрестности
х0-между
фиксированная
значение
точки
Расстояние
точками
хи
Функция
f(х)
тоже
примет
f(xаргумента
0точка,
)=хf(x
0 +∆x)-f(x
0),КОТОРАЯ
0 возьмём
f(х0)получило
значение
точку
х
хНАЗЫВАЕТСЯ
0 обозначим ∆х.Оно называется
ФУНКЦИИ
новое
значение:
0+∆x)
приращение
функци
вПРИРАЩЕНИЕМ
точке
∆х, иf(x
хновое
0
приращением
аргумента
и
И ОБОЗНАЧАЕТСЯ ∆f
значение
х равно
х0+∆х
равно
разности
между
х и х 0:
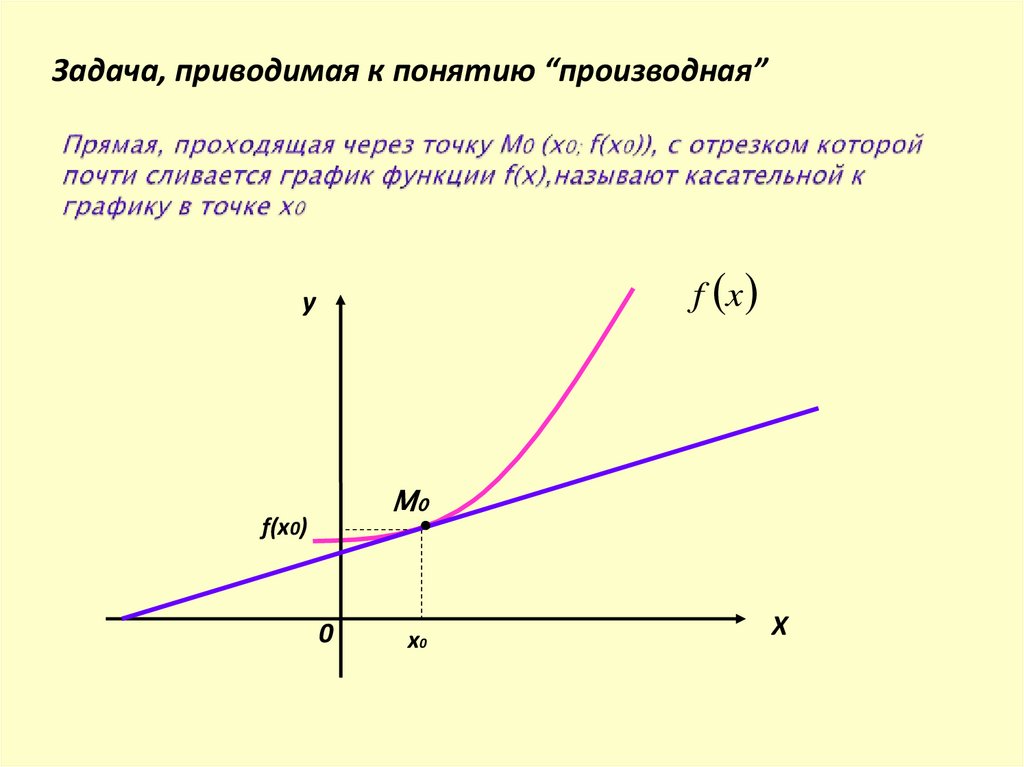
4. Прямая, проходящая через точку М0 (х0; f(х0)), с отрезком которой почти сливается график функции f(х),называют касательной к
Задача, приводимая к понятию “производная”f x
y
M0
f(x0)
0
x0
X
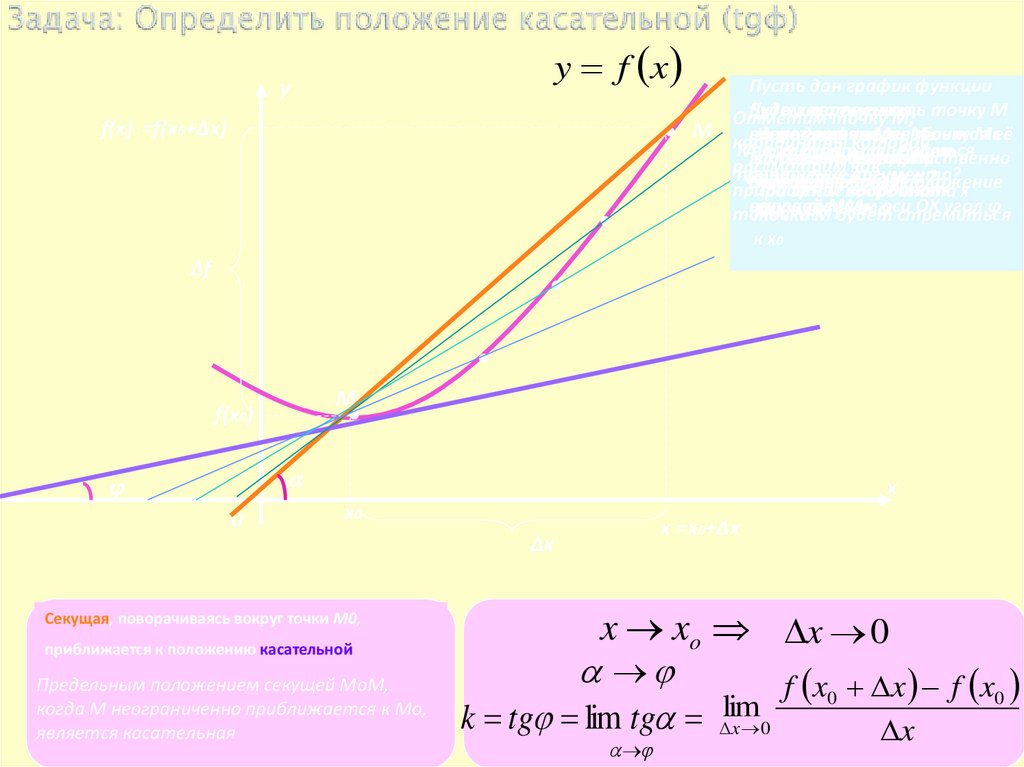
5. Задача: Определить положение касательной (tgφ)
y f xу
f(x) =f(x0+∆x)
М
Пусть дан график функции
f(х) и касательная,
Будем
перемещать
Отметим
точку М, точку М
проходящая
через
точку
М0её
вдоль
Черезграфика,
точки
Мприближая
иМ
0
координаты
которой
КА,которая
чему
будет
стремиться
к
какому
углу
будет
с
кпроведём
точке Мобразует
0.секущую,
Соответственно
рассмотрим
как
приращение
аргумента?
стремиться
уголположение
?с
положительным
будет
меняться
которая
образует
приращение
координат
При
этом
координата
х
направлением
оси
ОХ
угол
φ
секущей
ММ
0
осьюМОХ
стремиться
точки
0М угол
точки
будет
к х0
∆f
М0
f(x0)
φ
0
х
х0
х =x0+∆x
∆x
Секущая, поворачиваясь вокруг точки М0,
приближается к положению касательной
Предельным положением секущей МоМ,
когда М неограниченно приближается к Мо,
является касательная
x xo x 0
f x0 x f x0
lim
k tg lim tg x 0
x
6. Определение производной
Производной функции f в точке х0 называетсяпредел отношения приращения функции к
приращению аргумента при последнем
стремящимся к нулю:
f ( x0 x) f ( x0 )
f x lim
x O
x
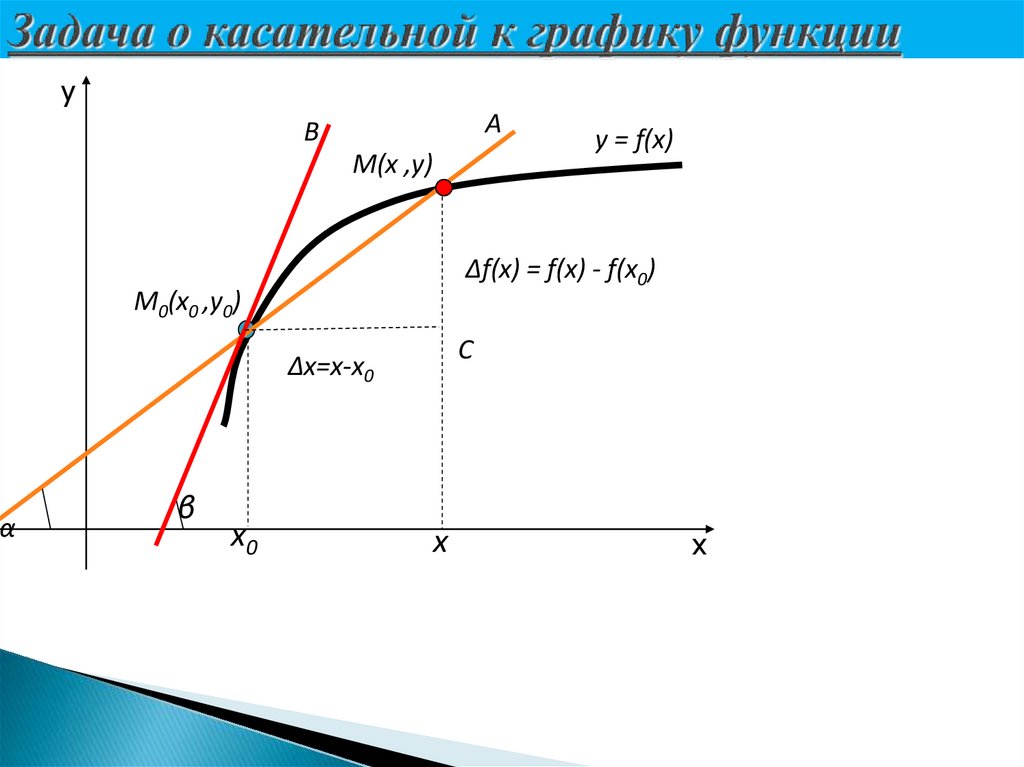
7. Задача о касательной к графику функции
yА
В
М(х ,у)
∆f(x) = f(x) - f(x0)
М0(х0 ,у0)
С
∆х=х-х0
α
β
x0
y = f(x)
x
x
8.
Физический смыслпроизводной x`(t) от
непрерывной функции
x(t) в точке t (0) – есть
мгновенная скорость
изменения величины
функции, при условии,
что изменение аргумента
Δt стремится к нулю.
9.
- Представьте, что вы летите в самолёте и у вас наруке часы. Когда Вы летите, Вы имеете скорость
равную скорости самолёта.
- А какая скорость у Вас и у самолёта в каждый
момент времени на Ваших часах?
– Скорость, как физическое понятие, это путь
самолёта, пройденный за единицу времени
(например, за час (км/час)), а у Вас, когда Вы
взглянули на часы прошло только мгновение. Таким
образом, мгновенная скорость (величина пути,
пройденного за мгновение) и есть производная
величина от функции, описывающей путь самолёта по
времени. Мгновенная скорость - это и есть
физический смысл производной.
10.
yy f (x)
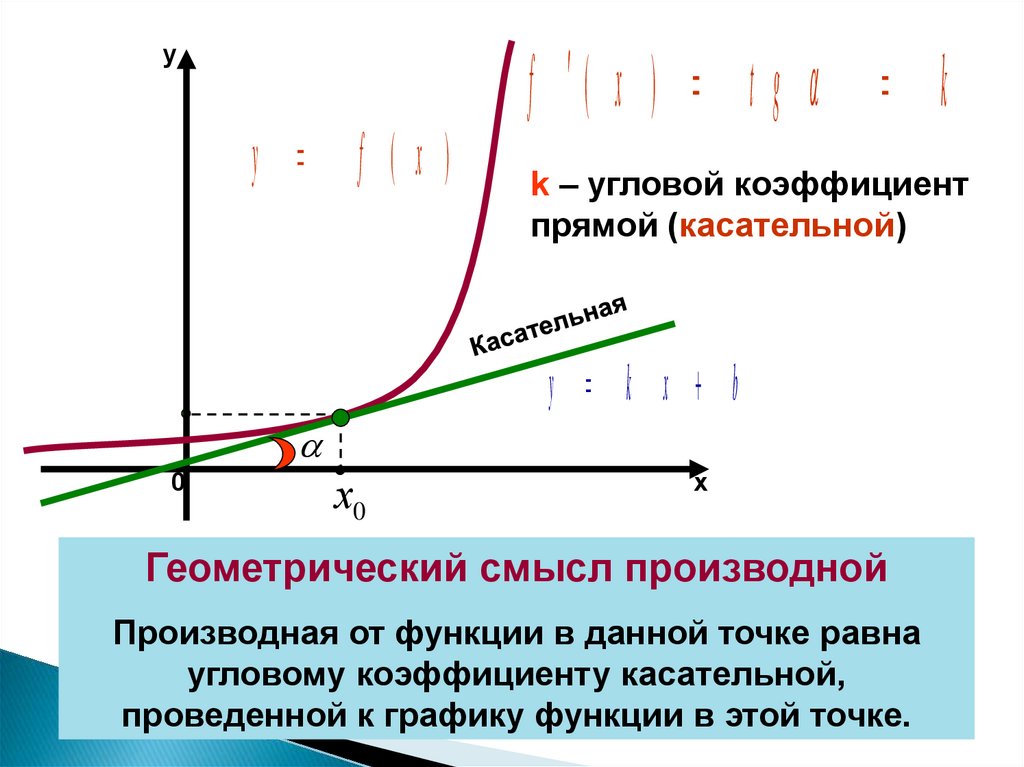
f ( x ) t g k
k – угловой коэффициент
прямой (касательной)
y k x b
0
х0
х
Геометрический смысл производной
Производная от функции в данной точке равна
угловому коэффициенту касательной,
проведенной к графику функции в этой точке.
11.
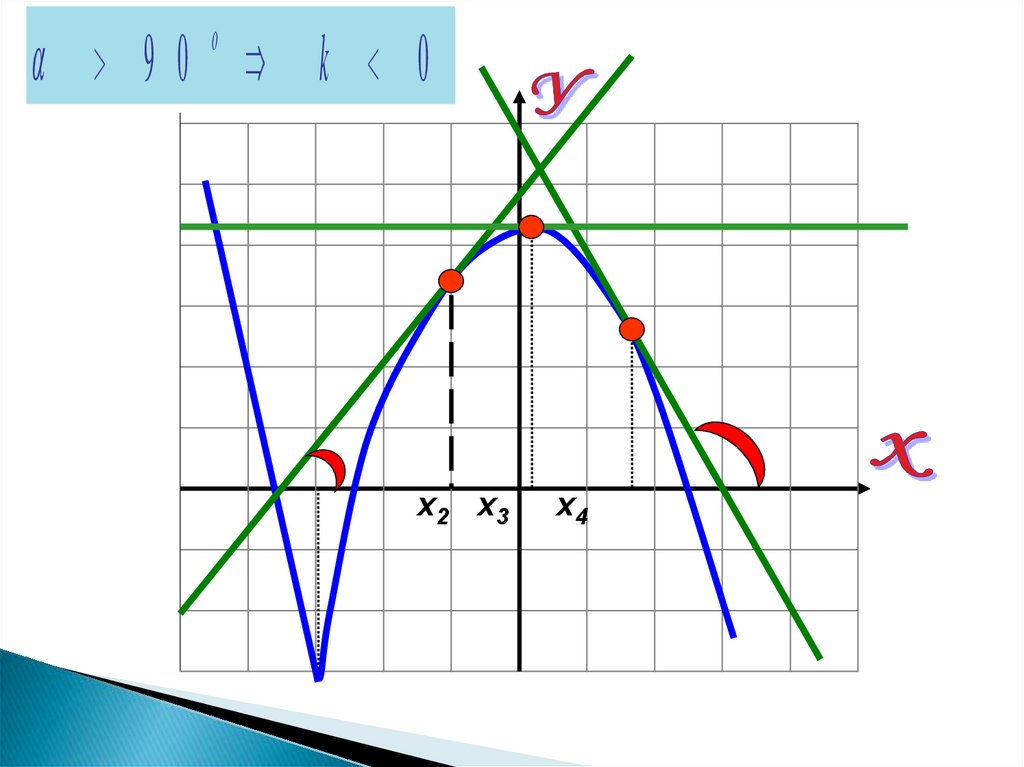
90 k 0o
х2 х3
х4
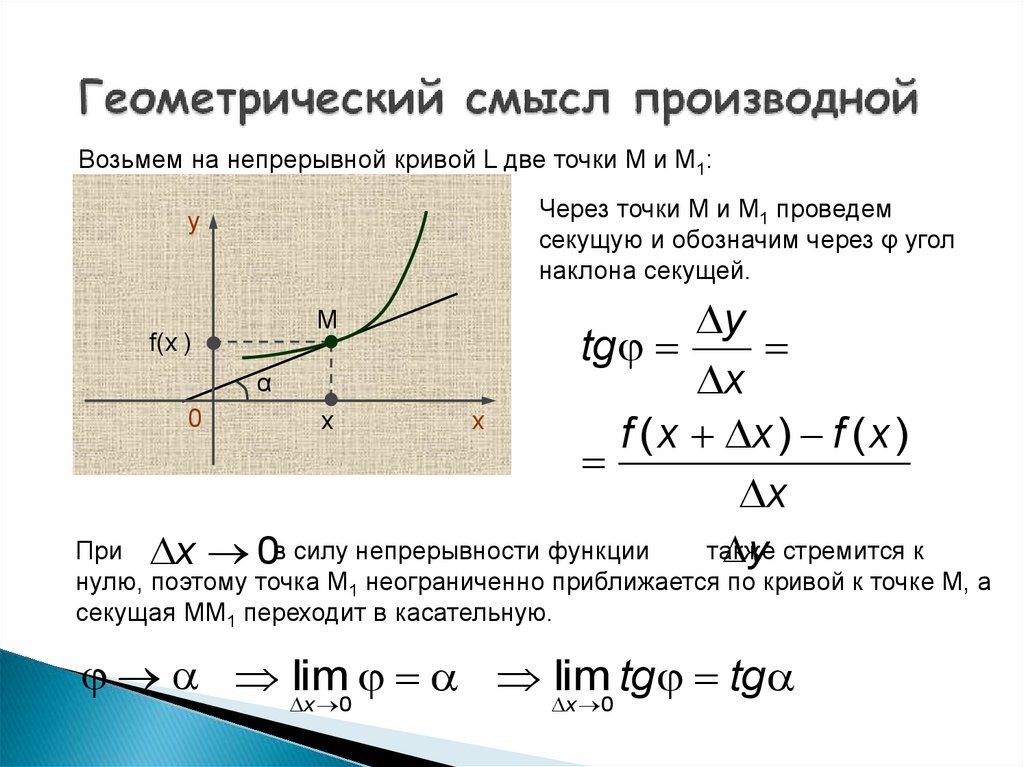
12. Геометрический смысл производной
Возьмем на непрерывной кривой L две точки М и М1:Через точки М и М1 проведем
секущую и обозначим через φ угол
наклона секущей.
y
М1
f(x+ Δx )
f(x )
α
0
y
М
М
x
φ
х
x+Δx
х
y
tg
x
f ( x x ) f ( x )
x
При x 0в силу непрерывности функции
также
y стремится к
нулю, поэтому точка М1 неограниченно приближается по кривой к точке М, а
секущая ММ1 переходит в касательную.
lim lim tg tg
x 0
x 0
13. Геометрический смысл производной
f ( x x ) f ( x )y
lim
tg
k
x 0
x
Производная f ’(x) равна угловому коэффициенту касательной к графику
функции y = f(x) в точке, абсцисса которой равна x.
y
Если точка касания М имеет координаты (x0; y0 ), угловой коэффициент
касательной есть k = f ’(x0 ).
Уравнение прямой с угловым коэффициентом:
y y 0 кf '((xx-0 )(
x 0x)- x 0 )
Уравнение
Уравнение
касательной
нормали
Прямая, перпендикулярная касательной в точке касания, называется
нормалью к кривой.
f ' ( x0 )
1
1
1
k норм
y y0
( x x0 )
k кас
f ' ( x0 )
f ' ( x0 )
14. Касательная к графику функции
Уравнение касательнойf(x)= f (x0)+ f ´(x0)(x- x0)
Kоэффициент угла
наклона касательной
k = f ´(x0) = tgα
15. Правило вычисления производных.
(f(х) ± g( х))΄= f(х)΄± g( х)΄(Сf(х))΄= С( f(х))΄
(f(х)·g( х))΄= f(х)΄g( х)+ f(х)g( х)΄
(f(х)/g(х))΄= (f(х)΄g( х)–f(х)g( х)΄)/g( х) 2
16. Производная сложной функции.
g (f(x ))΄ = g΄(f(x))·f ΄(x)17. Основные формулы
k0
1
1/х
18. Производные тригонометрических функций.
(sin x) ΄ =(cos x) ΄ =
(tg x) ΄ =
(ctg x) ΄ =
19. Связь между непрерывностью и дифференцируемостью функции
ТеоремаЕсли функция f(x) дифференцируема в некоторой точке , то она
непрерывна в ней.
Доказательство:
Пусть функция y = f(x) дифференцируема в некоторой точке х,
следовательно существует предел:
y
y
( x )
lim
f
f ( x ) ( x )
x 0
x
x
где ( x ) 0 при x 0
По теореме о связи
функции, ее предела и
y
0
y f ( x ) x ( x ) x lim
бесконечно
малой
x 0
Функция y = f(x) – непрерывна.
функции
Обратное утверждение не верно: непрерывная функция может не иметь
производной.
20. Производные основных элементарных функций
1Степенная функция:
y x
Придадим аргументу x приращение
приращение:
y x x x
n
n
n Z
x функция получит
, тогда
n
Формула бинома Ньютона:
n( n 1) n 2 2
a b a na b
a b
2!
n( n 1) ( n k 1) n k k
a b bn
k!
n
n
n 1
K – факториал
k! 1 2 3 k
21. Производные основных элементарных функций
По формуле бинома Ньютона имеем:y x x x n
n(n 1) n 2 2
n
n 1
n
n
( x nx x
x x x ) x
2!
y
n(n 1) n 2
n 1
Тогда:
nx
x x x n 1
x
2!
y
n 1 n(n 1) n 2
n 1
lim
lim
nx
x
x
x
x 0
x x 0
2!
n
nx n 1
x ' nx
n
n 1
22. Производные основных элементарных функций
2Логарифмическая функция:
y ln x
x
x x
y ln x x ln x ln
ln 1
x
x
x
x
ln 1
1
1
y
x
x lim
lim
lim
lim
x 0
x 0
x 0
x 0
x x
x
x
x
1
ln x '
x
x x
ln 1
~
x
x
Аналогично выводятся правила дифференцирования
других
основных
при
x
0
элементарных функций.
23. Правила дифференцирования
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b)функции, С – постоянная.
(C ) 0
(u v ) u v
(u v ) u v u v (C u ) C u
(u v w ) u v w u v w u v w
u u v u v
C
C
v
2
2
v
v
v
v
24. Производная сложной функции
Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x)) – сложная функция спромежуточным аргументом u и независимым аргументом x.
Теорема
Если функция u = φ(x) имеет производную
в точке
u x x а функция y =
f(u) имеет производную
в соответствующей
y u точке u , то сложная
функция имеет производную
, которая находится
y по формуле:
x
y x y u u x
Это правило остается в силе, если промежуточных аргументов несколько:
y f (u );
u (v );
v g( x )
y x y u uv v x
y f ( (g ( x )))

















 Математика
Математика








