Квантовая физика. Состояние квантово-механической частицы

1.

Физика. 2 курс. 4 семестр
Специалитет
Лекция 3. Квантовая физика
Состояние квантово-механической
частицы:
- Частица и потенциальные
барьеры
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела, параграфа
Номер слайда
Введение
3
Раздел 1. Частица и потенциальная «ступенька»
4
1.1. Понятие потенциальной «ступеньки»
5
1.2. Постановка задачи
6
1.3. Случай 1: полная энергия частицы больше высоты «ступеньки»
7
1.3.1. Случай 1: соотношения амплитуд волн
8
1.3.2. Случай 1: коэффициенты отражения и прохождения
9
1.4. Случай 2: полная энергия частицы меньше высоты «ступеньки»
10
1.4.1. Случай 2: полное отражение частицы
11
1.4.2. Случай 2: проникновение частицы под барьер
12
Раздел 2. Частица и потенциальный барьер конечной ширины
13
2.1. Понятие туннельного эффекта
14
2.2. Вероятность прохождения частицы через барьер
15
2

3.

Введение
В 3-ей лекции продолжается изучение состояния квантово-механической частицы в различных
потенциальных полях U(x). Напомню, во 2-ой лекции рассматривалось потенциальное поле в виде
прямоугольной бесконечной «ямы». Сейчас рассмотрим более реалистические случаи:
- потенциальное поле в виде «ступеньки»;
- потенциальное поле в виде барьера конечной ширины.
Второй случай имеет множество практически важных следствий: радиоактивный распад с
испусканием альфа-частицы, спонтанное деление ядер, холодная эмиссия электронов из металла и
многие другие.
Рассмотрение ведётся, как и полагается в квантовой физике, с использованием уравнения
Шредингера и, по-прежнему, для стационарных условий и для одномерного случая.
3

4.

Раздел 1. Частица и потенциальная «ступенька»
4

5.

1. Частица и потенциальная «ступенька»
1.1. Понятие потенциальной «ступеньки»
Потенциальное поле в виде «ступеньки» выглядит так:
«Ступенька» имеет конечную высоту: U0 < ∞.
«Ступенька» имеет бесконечную длину при х ≥ 0.
5

6.

1. Частица и потенциальная «ступенька»
1.2. Постановка задачи
С некоторой долей условности считаем, что на «ступеньку» слева налетает частица с
полной энергией Е, имеющая соответствующую дебройлевскую волну. Иногда говорят: слева
«падает волна».
Условность постановки задачи состоит в том, что мы рассматриваем стационарные решения, но
используем термины «налетает», «падает», связанные с движением. Это – для наглядности.
Предполагается, что «налетание», «падение» произошли очень давно при t = -∞, а сейчас мы
рассматриваем установившее состояние частицы (волны), когда начальное движение уже «забылось».
Частица (или волна) отражается от барьера.
Требуется найти: связь амплитуд падающей и отражённой волн, а также коэффициенты
отражения R. Для этого надо найти Ψ(x) – волновую функцию до «ступеньки» и после неё.
Как всегда в квантовой физике, для решения используем уравнение Шредингера:
Удобнее использовать уравнение Шредингера в ином виде:
где k2 = 2m(E-U)/ℏ2,
U – потенциальная энергия, зависит от х.
6

7.

1. Частица и потенциальная «ступенька»
1.3. Случай 1: полная энергия частицы больше высоты «ступеньки»
U
E
Полная энергия частицы больше высоты
«ступеньки»:
E > U0
U0
I
0
x
II
Общий вид решения уравнения Шредингера:
Область I, х < 0: Ψ1(x) = а1exp(ik1x) + b1exp(-ik1x)
k12= 2mE/ℏ2 – значение U = 0 - см. слайд 5.
Первое слагаемое – падающая на «ступеньку» волна с амплитудой а1
Второе слагаемое – отражённая от «ступеньки» волна с амплитудой b1 (знак «минус» перед х!)
Область II, x ≥ 0: Ψ2(x) = а2exp(ik2x) + b2exp(-ik2x)
k22= 2m(E-U0)/ℏ2 – значение U = U0 см. слайд 5.
Первое слагаемое – проходящая над «ступенькой» волна с амплитудой а2
Второе слагаемое – отражённая волна с амплитудой b2
По физсмыслу, в области II отражённой волны нет (волна «падает» слева), поэтому b2 = 0.
7

8.

1. Частица и потенциальная «ступенька»
1.3.1. Случай 1: соотношения амплитуд волн
Найдём соотношения амплитуд волн: a1, b1, a2 (напомню, что b2=0), и их связь с волновыми
числами: k1 и k2.
Параметры k1 и k2, являясь волновыми числами, также характеризуют вид потенциала U(x) через соотношение
заданного значения энергии частицы и значения потенциала в каждой точке пространства: Е – U(х).
Для этого воспользуемся условиями гладкости, т.е. непрерывности самой пси-функции и её
производной на границе «ступеньки» – в точке х=0:
Ψ1(x=0) = Ψ2(x=0),
отсюда следует: a1 + b1 = a2
dΨ1(x=0) / dx = dΨ2(x=0) / dx, отсюда следует: a1∙k1 - b1∙k1 = a2∙k2
(проверьте прямой подстановкой)
(проверьте прямой подстановкой)
Из этих условий следуют соотношения амплитуд волн:
b1 / a1 = (k1 – k2) / (k1 + k2)
a2 / a1 = 2k1 / (k1 + k2)
Соотношения амплитуд волн зависят от комбинации волновых чисел до и после «ступеньки».
Замечание: выглядит странным первое соотношение, в котором отношение амплитуд в 1-ой
области (b1 / a1) оказалось зависимым от волнового числа как в первой (k1), так и во второй (k2)
областях. Но это на первый взгляд, привыкайте.
8

9.

1. Частица и потенциальная «ступенька»
1.3.2. Случай 1: коэффициенты отражение и прохождения
Определение. Коэффициент отражения R – это вероятность отражения частицы от
потенциального барьера.
Величина коэффициента отражения рассчитывается как отношение квадратов модулей амплитуд
отражённой от «ступеньки» и падающей на «ступеньку» волн:
R = [mod(b1)]2 / [mod(a1)]2 = [(k1 – k2) / (k1 + k2)]2
Физсмысл: отражение волны от «ступеньки» происходит (R ≠ 0), хотя «высота» волны (Е)
больше высоты «ступеньки» (E > U0).
Определение. Коэффициент прохождения (или: пропускания, или: прозрачности) D – это
вероятность прохождения частицы «над» энергетической «ступенькой».
Величина коэффициента прохождения рассчитывается так (промежуточные выкладки опущены):
D = 4∙(k1∙k2) / (k1 + k2)2
Очевидно, что существует связь: R + D = 1.
Проверьте прямой подстановкой.
Величины R и D могут быть только положительны или равны нулю.
Сравните: в классической физике при E > U0 отражения быть не может, значение R = 0. Частица
как бы «не замечает» «ступеньку» и поэтому не отражается.
9

10.

1. Частица и потенциальная «ступенька»
1.4. Случай 2: полная энергия частицы меньше высоты «ступеньки»
U
Полная энергия частицы меньше высоты
«ступеньки»:
E < U0
U0
E
I
0
x
II
Общий вид решения уравнения Шредингера такой же, как в случае 1 – см. слайд 7:
Область I, х < 0:
Ψ1(x) = а1exp(ik1x) + b1exp(-ik1x)
k12= 2mE/ℏ2,
k1 >0
Область II, x ≥ 0:
Ψ2(x) = а2exp(ik2x) + b2exp(-ik2x)
k22= 2m(E-U0)/ℏ2 < 0, значит, k2 – мнимое число.
Кроме того, по физсмыслу, в области II отражённой волны нет, поэтому b2 = 0.
10

11.

1. Частица и потенциальная «ступенька»
1.4.1. Случай 2: полное отражение частицы
Нетрудно показать, что отношение амплитуд отражённой и падающей волн остаётся тем же:
b1 / a1 = (k1 – k2) / (k1 + k2),
k1 – действительное положительное число, k2 – мнимое число.
Коэффициент отражения в таком случае рассчитывается так:
R = [mod(k1 – k2)]2 / [mod(k1 + k2)]2
Числа (k1 – k2) и (k1 + k2) – есть комплексно сопряжённые числа (напомню, k2 – мнимое число).
Тогда:
R = 1, т.е. отражение будет полным.
Покажите, что R = 1, самостоятельно.
По физсмыслу, этот результат является совершенно естественным. Действительно, падающая
на потенциальный барьер волна, с энергией меньше высоты барьера, должна от него отразиться
полностью. Это и получено в результате квантово-физического рассмотрения.
В данном случае результат квантовой физики совпал со здравым смыслом! Но это ещё не
конец вопроса…
11

12.

1. Частица и потенциальная «ступенька»
1.4.2. Случай 2: проникновение частицы под барьер
В области II (х>0) пси-функция записывается так (см. слайд 10):
Ψ2(x) ~ exp(ik2x),
амплитуда а2 опущена для простоты.
Величина k2 мнимая, значит, её можно представить так:
k2 = i∙k,
где k = [2m(U0 - E)]1/2 / ℏ - действительное положительное число
Обратите внимание на изменение знаков в круглых скобках, обычно (сл.10) писали E-U0.
Тогда: Ψ2(x) ~ exp(-kx),
k – действительное положительное число.
Значит, вероятность нахождения частицы (волны) в подбарьерной области при х>0 составляет:
W(х) ~ [Ψ2(x)]2 ~ exp(-2kx)
По мере удаления вглубь, т.е. вправо от границы «ступеньки» х=0, вероятность быстро снижается,
но всё же частица существует там, где её не может быть по классическим представлениям.
Это – чисто квантово-физический эффект. Несмотря на такое подбарьерное проникновение,
коэффициент отражения частицы от барьера равен 1! Подумайте над этим «противоречием».
Самостоятельно оцените характерную глубину проникновения электрона под барьер с параметром: U0 – E = 10-3 эВ. При
такой глубине проникновения вероятность обнаружения частицу меньше в е раз по сравнению с вероятностью на границе барьера.
12

13.

Раздел 2. Частица и потенциальный барьер
конечной ширины
13

14.

2. Частица и потенциальный барьер конечной ширины
2.1. Понятие туннельного эффекта
В предыдущем разделе показано, что квантовая частица может проникать под барьер. На этом
основывается туннельный эффект.
Определение. Туннельный эффект – это способность квантовой частицы в силу своих волновых
свойств проходить сквозь потенциальный барьер конечной ширины и конечной высоты.
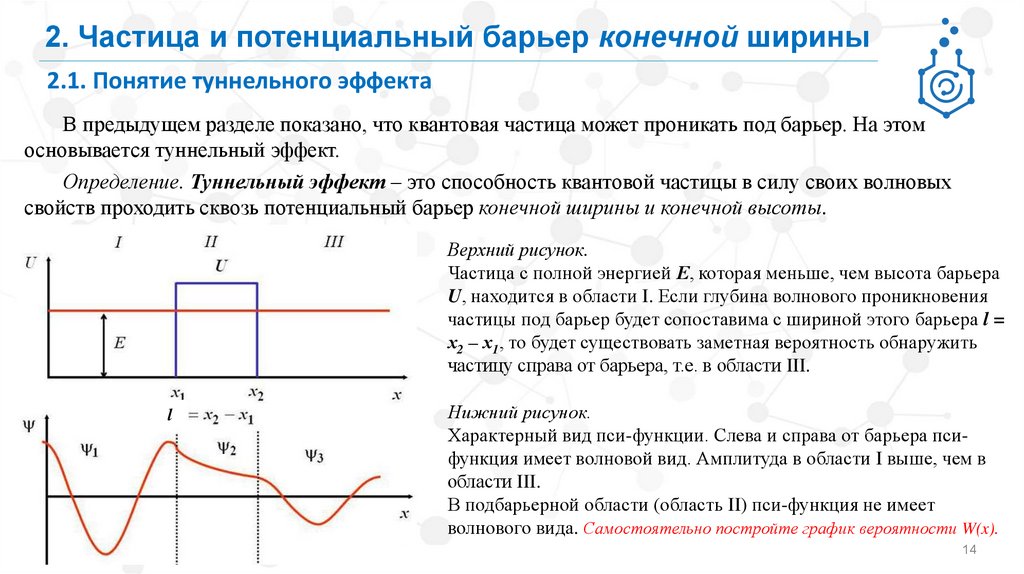
Верхний рисунок.
Частица с полной энергией Е, которая меньше, чем высота барьера
U, находится в области I. Если глубина волнового проникновения
частицы под барьер будет сопоставима с шириной этого барьера l =
х2 – х1, то будет существовать заметная вероятность обнаружить
частицу справа от барьера, т.е. в области III.
l
Нижний рисунок.
Характерный вид пси-функции. Слева и справа от барьера псифункция имеет волновой вид. Амплитуда в области I выше, чем в
области III.
В подбарьерной области (область II) пси-функция не имеет
волнового вида. Самостоятельно постройте график вероятности W(x).
14

15.

2. Частица и потенциальный барьер конечной ширины
2.2. Вероятность прохождения частицы через барьер
Определение. Коэффициент прохождения (или: коэффициент прозрачности барьера) D – это
отношение квадратов амплитуд прошедшей сквозь барьер и падающей на барьер волн.
Часто величину D рассматривают как вероятность прохождения частиц через энергетический
барьер.
l – ширина барьера прямоугольной формы
Для потенциального барьера произвольной формы (рисунок справа)
формула для расчёта коэффициента прохождения (или: вероятности):
15

16.

Примерно так частица пробирается по туннелю,
преодолевая потенциальный барьер конечной ширины. (Не проверяйте сами!)
16

17.

Спасибо за внимание