Частица в одномерной глубокой потенциальной яме. Прохождение частицы через потенциальный барьер. Туннельный эффект. (Лекция 5)

1.

Кафедра физики
ЛЕКЦИЯ 5
ПЛАН ЛЕКЦИИ
Примеры решения квантовых задач:
- Частица в одномерной глубокой потенциальной яме.
- Прохождение частицы через потенциальный барьер. .
Туннельный эффект.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1

2.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Задача: найти собственные значения энергии и соответствующие им
собственные функции для частицы, находящейся в бесконечно
глубокой одномерной потенциальной яме.
Потенциальная яма - область пространства, в которой
потенциальная энергия частицы достигает локального минимума.
U
U=
Одномерный
случай:
частица
движется только вдоль оси х.
U=
Пусть
движение
ограничено
непроницаемыми
для
частицы
отвесными стенками с координатами
х = 0 и х = l.
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
2

3.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Вид потенциальной энергии: U = 0 при 0 ≤ х ≤ l ;
U = при
х 0 и х l.
Вид уравнения Шредингера:
За пределы потенциальной
частица попасть не может.
U
U=
2 2 m
2 E U 0
2
x
U=
ямы
Поэтому вероятность обнаружения
частицы вне ямы равна нулю.
Следовательно, за пределами ямы 0
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
3

4.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
2m
2 E U 0
2
x
2
Функция должна быть непрерывной,
следовательно, она должна быть равна
нулю и на границах ямы:
0 l 0
U
U=
В области х 0 и х l уравнение
Шредингера имеет вид:
U=
2 2 m
2 E 0 ,
2
x
0
l
x
поскольку в этой области U = 0.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
4

5.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Решение - как в предыдущей задаче.
2 2 m
2 E U 0
2
x
2m
k 2 E
2
2
k
0
2
x
2
2 2 m
2 E 0
2
x
Это уравнение колебаний. Решение:
U
U=
x a sin kx
U=
а, k и α- константы.
Определим α и k из граничных условий:
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
0 l 0
5

6.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
2 2 m
2 E U 0
2
x
2m
2 E 0
2
x
2
2
k
0
2
2
0 a sin 0
0
Второе граничное условие - l 0 :
l a sin kl 0
Это соотношение выполняется при условии:
x
x a s in k x
Из условия 0 0 получим:
Исследуем полученные
решения.
1. Энергия частицы в
потенциальной яме.
kl n
(n = 1, 2, 3, …).
2m
2
k 2 E
E
2 2
2 ml
2
n
,
2
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
n
k
l
k 2 2
E
2m
(n = 1, 2, 3, …)
6

7.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
E
2 2
2 ml
2
n
,
2
n = 1, 2, 3, …
Таким
образом,
стационарное
уравнение
Шредингера
удовлетворяется только при собственных значениях энергии,
зависящих от целого числа n.
Следовательно, энергия En частицы принимает лишь дискретные
значения, т.е. квантуется.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
7

8.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
Квантованные значения энергии En - это уровни энергии, а число n,
определяющее энергетические уровни частицы, - главное квантовое
число.
n=4
E
E4
Универсальный принцип природы: всякий
объект
стремится
к
состоянию
с
минимальной энергией.
n=3
E3
Это характерно и для микрочастиц: наиболее
устойчивым
является
состояние
с
n=2
E2 минимальной энергией.
n=1
E
1
Стационарное состояние с минимальной энергией - основное
состояние (основной уровень). Все остальные стационарные
состояния (уровни) - возбужденные.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
8

9.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
2. Определим собственные значения функции x .
Подставим в уравнение x a sin kx значение
n x a sin n x / l
n
k
l
Коэффициент a определим из условия нормировки ( dV) 1):
2
n x
a 2 sin2
dx 1
l
0
l
V
(Задача одномерная, интеграл по объему
заменен на интеграл по координате х).
a 2l
1.
Результат интегрирования:
2
Окончательно:
n x
Отсюда a 2 l .
2 n
sin
x
l
l
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
(n = 1, 2, 3, …)
9

10.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
2 n
n x
sin
x
(n = 1, 2, 3, …)
l
l
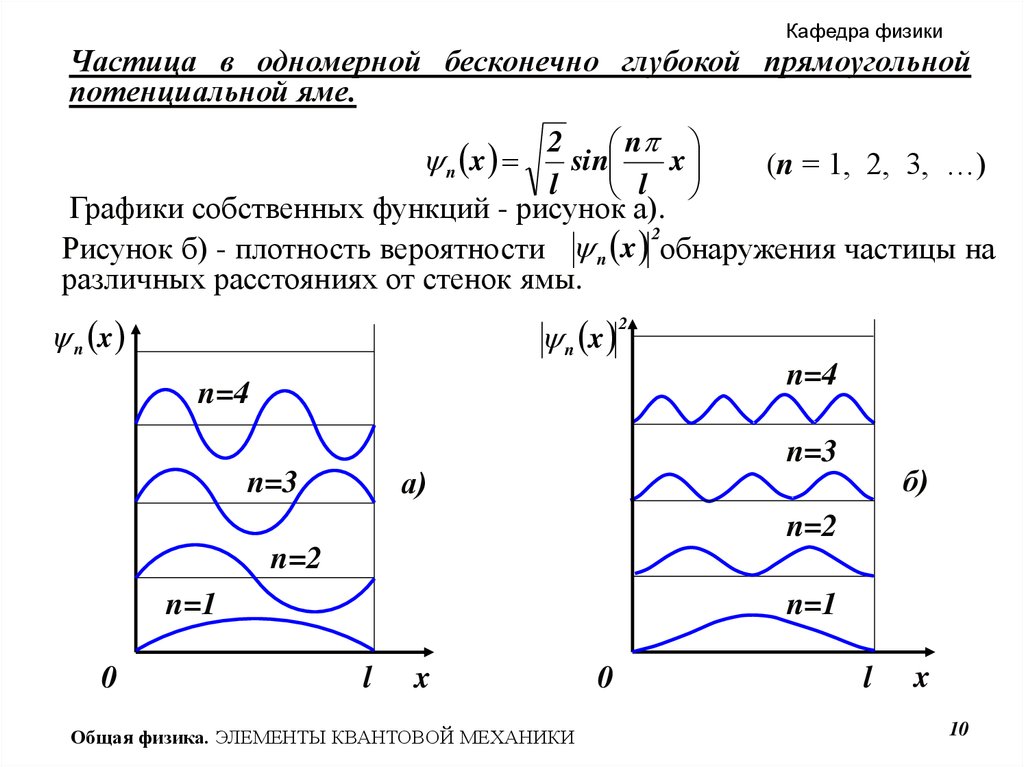
Графики собственных функций - рисунок а).
2
Рисунок б) - плотность вероятности n x обнаружения частицы на
различных расстояниях от стенок ямы.
n x
n x
2
n=4
n=4
n=3
а)
n=3
б)
n=2
n=2
n=1
0
n=1
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
0
l
x
10

11.

Кафедра физики
Частица в одномерной бесконечно глубокой прямоугольной
потенциальной яме.
n x
n x
2
n=4
n=4
n=3
а)
n=3
б)
n=2
n=2
n=1
0
n=1
l
x
0
l
x
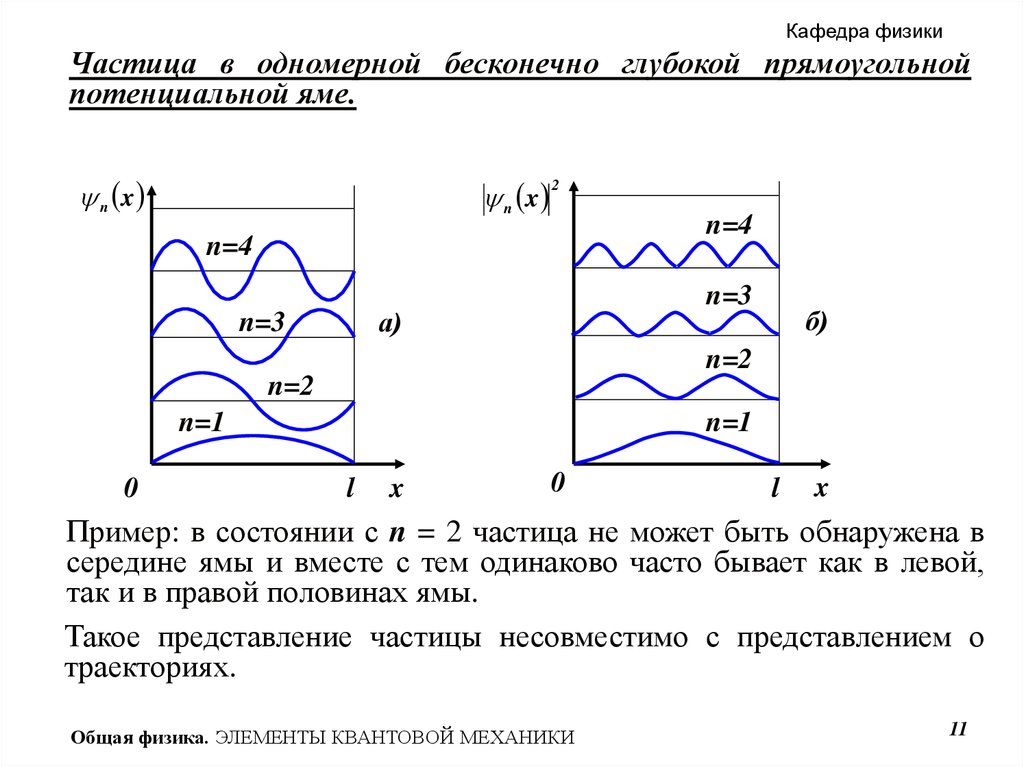
Пример: в состоянии с n = 2 частица не может быть обнаружена в
середине ямы и вместе с тем одинаково часто бывает как в левой,
так и в правой половинах ямы.
Такое представление частицы несовместимо с представлением о
траекториях.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
11

12.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
Определения.
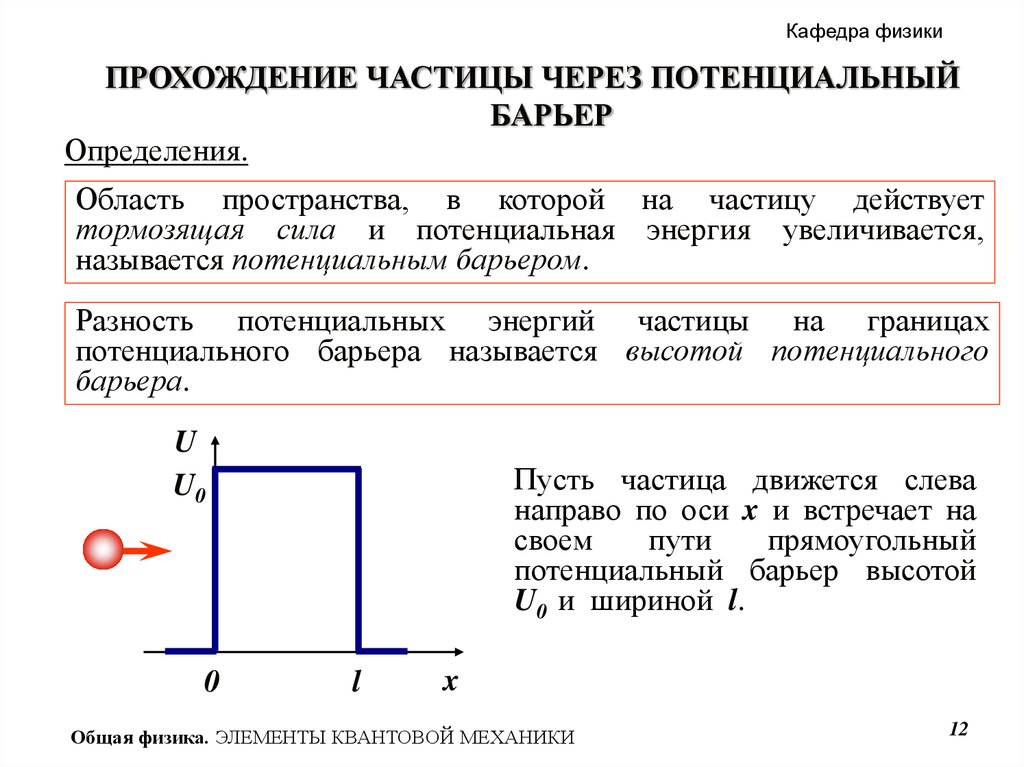
Область пространства, в которой на частицу действует
тормозящая сила и потенциальная энергия увеличивается,
называется потенциальным барьером.
Разность потенциальных энергий частицы на границах
потенциального барьера называется высотой потенциального
барьера.
U
U0
0
Пусть частица движется слева
направо по оси x и встречает на
своем
пути
прямоугольный
потенциальный барьер высотой
U0 и шириной l.
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
12

13.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
Классические представления о поведении частицы.
1. E > U0 . Частица беспрепятственно проходит над барьером.
E
0 ≤ х ≤ l. Скорость частицы
уменьшается; х > l - скорость
частицы постоянна.
U
U0
0
l
x
2. E < U0 . Частица отражается от
барьера и летит в обратную
сторону. Сквозь барьер частица
проникнуть не может.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
13

14.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
Поведение частицы в квантовой механике.
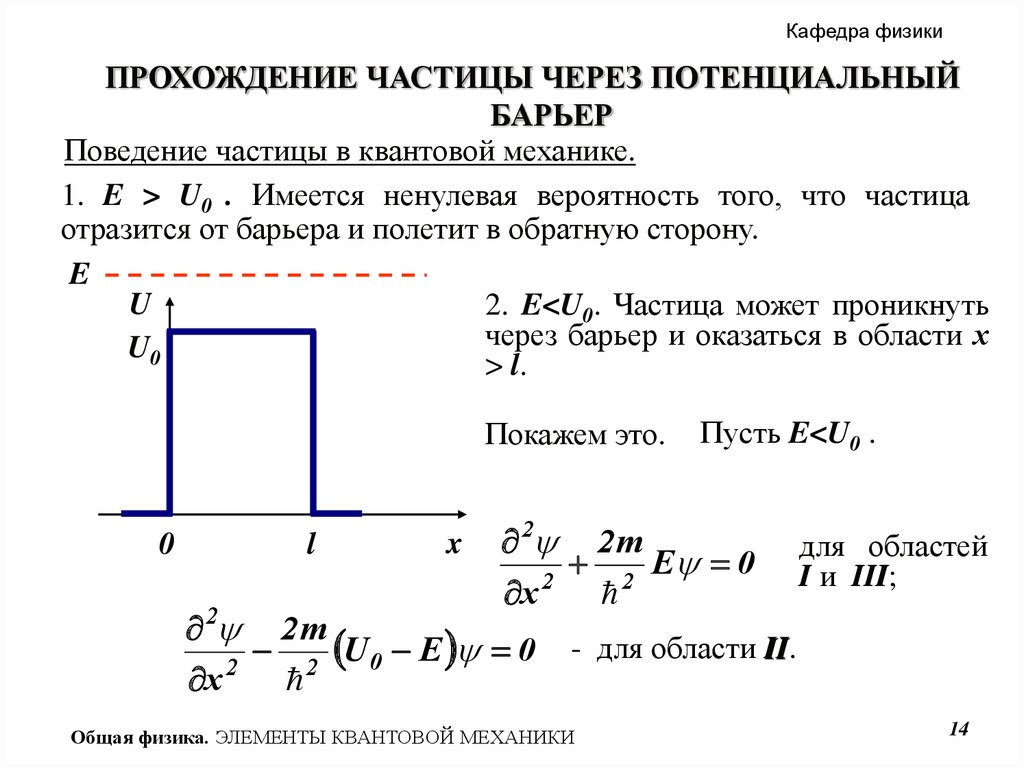
1. E > U0 . Имеется ненулевая вероятность того, что частица
отразится от барьера и полетит в обратную сторону.
E
U
2. E<U0. Частица может проникнуть
через барьер и оказаться в области х
U0
> l.
Покажем это.
0
l
x
2
x 2
2 2 m
2 U 0 E 0
2
x
2m
2
Пусть E<U0 .
E 0
для областей
I и III;
III
- для области II.
II
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
14

15.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
U
БАРЬЕР
U0
2
E
I
2
II
2m
2
E 0 - для областей I и III
x
2 2 m
2 U 0 E 0 - для области II
2
x
III
0
l
Введем обозначения:
x
k2
2m
E,
2
2m
2 U 0 E
2
С учетом этих обозначений:
2 1 , 3
2
k
1 ,3 0
2
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
2 2
2
2 0
2
x
15

16.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
U
БАРЬЕР
2 1 , 3
U0
2
k
1 ,3 0
2
x
E
I
III
II
0
l
x
2 2
2
2 0
2
x
Как решить эти уравнения?
Записанные уравнения – это линейные дифференциальные
однородные уравнения второго порядка с постоянными
коэффициентами.
Заглянуть в соответствующий раздел курса
«Элементы математического анализа»!
Такие уравнения решают методом подстановки.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
16

17.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
U
БАРЬЕР
U0
2
1 ,3
E
I
II
x 2
III
x
0
l
Решение уравнений записывается в виде
постоянная величина.
Итог - решения уравнений для
трех выделенных областей :
k 2 1 , 3 0
2 2
2
2 0
2
x
exp x , где
-
1 A1 exp ikx B1 exp ikx
2 B2 exp x
3 A3 exp ikx
Нужно найти значения констант А1 , А3 , В1 , В2 .
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
17

18.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
1
2
3
A 1 e x p ik x B 1 e x p ik x
B 2 ex p x
A 3 e x p ik x
Константы определяются «сшиванием» уравнений на границах
областей с помощью граничных условий: пси-функция должна
удовлетворять условию ограниченности, непрерывности, не
иметь изломов, т.е. должна быть гладкой.
Эта задача решена. Рассмотрим лишь некоторые выводы.
При условии Е<U0 (полная энергия частицы меньше высоты
потенциального барьера), законы классической физики однозначно
не разрешают частице проникнуть сквозь барьер.
С позиций квантовой механики частица имеет отличную от нуля
вероятность прохождения через потенциальный барьер конечной
ширины.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
18

19.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
1
2
3
A 1 e x p ik x B 1 e x p ik x
B 2 ex p x
A 3 e x p ik x
В областях 1 и III общие решения представляют собой
суперпозицию волн, распространяющихся в положительном
(решение вида exp ikx ) и отрицательном (решение вида exp ikx )
направлениях оси х.
В области III - за барьером – есть только проходящая волна.
Вспомним, что волны, которые ассоциируются со свободно
движущимися частицами, получили название волн де Бройля.
В области II функция не соответствует плоской волне.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
19

20.

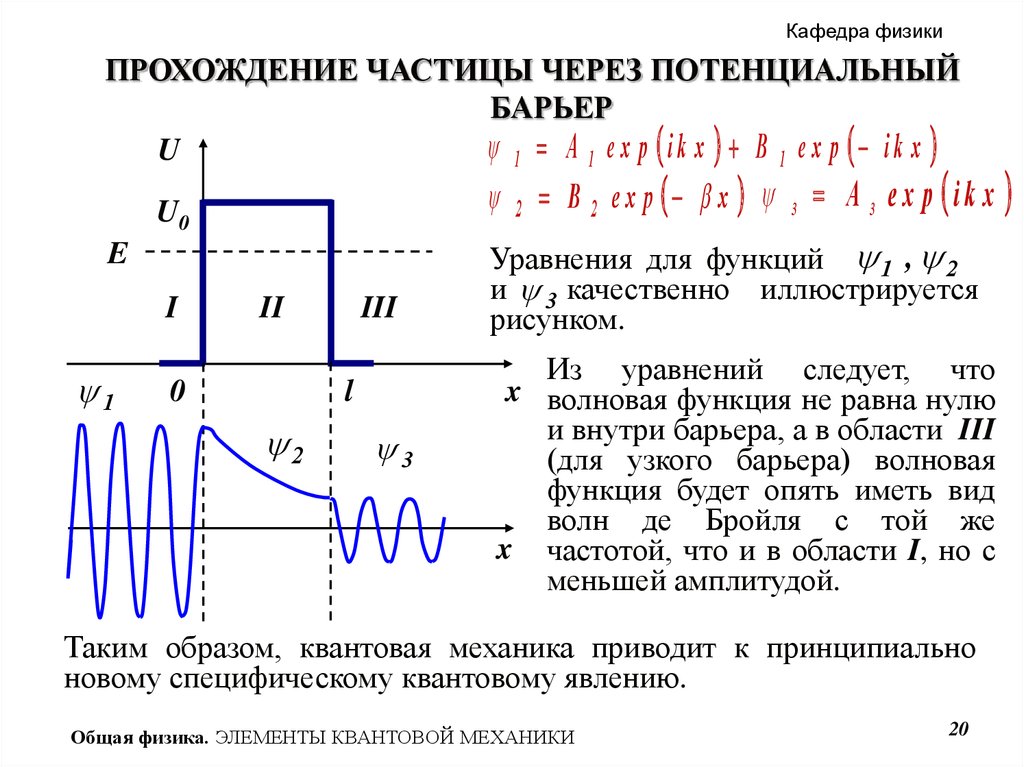
Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
1 A 1 e x p ik x B 1 e x p ik x
U
U0
E
I
1
II
0
III
l
2
3
2
B 2 ex p x
3
A 3 e x p ik x
Уравнения для функций 1 , 2 .
и 3 качественно иллюстрируется
рисунком.
Из уравнений следует, что
x волновая функция не равна нулю
и внутри барьера, а в области III
(для узкого барьера) волновая
функция будет опять иметь вид
волн де Бройля с той же
x частотой, что и в области I, но с
меньшей амплитудой.
Таким образом, квантовая механика приводит к принципиально
новому специфическому квантовому явлению.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
20

21.

Кафедра физики
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ
БАРЬЕР
При преодолении потенциального барьера частица как бы
пробивает
«туннель» в барьере. Это явление называется
туннельным эффектом.
Вероятность прохождения частицы через барьер
определяется отношением квадратов модулей
амплитуд прошедшей и падающей волн:
D
A3
2
A1
2
и называется коэффициентом прохождения (или коэффициентом
прозрачности).
По аналогии можно ввести и коэффициент
отражения частицы от барьера:
Очевидно, что
R
B1
2
A1
2
D R 1
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
21