Кручение. Расчеты на прочность

1.

ЛЕКЦИЯ №5
1
КРУЧЕНИЕ

2.

РАСЧЕТЫ НА ПРОЧНОСТЬ
2
Расчет на прочность сводится к требованию, чтобы наибольшие
напряжения в элементе конструкции не превосходили некоторой
допускаемой величины.
Методы
расчетов на
прочность
Метод
допускаемых
напряжений
Метод
предельных
состояний
Метод
разрушающих
нагрузок

3.

РАСЧЕТЫ НА ПРОЧНОСТЬ
3
Расчеты на прочность
проектировочные.
бывают
двух
видов:
проверочные
и
Во всех случаях при проведении расчетов на прочность решается одна
из трех задач:
1.
проверка выполнения условия прочности: проверка величины
максимальных напряжений при заданных размерах конструкции и
форме сечений ее элементов, нагрузке и свойствах материалов;
2.
определение размеров сечения: производится для сечения заданной
формы при известной нагрузке и свойствах материалов;
3.
определение допускаемой нагрузки: определяется грузоподъемность
конструкции при заданных форме и размерах ее элементов и свойствах
материалов.

4.

МЕТОД ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ
4
Расчёт ведётся по величине максимальных напряжений, возникающих в
опасной точке нагруженной конструкции.
Максимальное расчетное напряжение сравнивают с допускаемым
напряжением. При этом допускаемое напряжение определяют исходя из
величины коэффициента запаса.
σL – некое предельное напряжение,
Условие
max L
[σ] – допускаемое напряжение,
прочности:
n
n – коэффициент запаса.
Сечение, в котором действует максимальное напряжение, называется
опасным сечением. Для него и записывается условие прочности.
При проектном расчёте задаются значение коэффициента запаса и,
исходя из него, определяются «безопасные» размеры детали.
При проверочном расчёте определяют фактическое значение
коэффициента запаса и сравнивают его с требуемым значением.

5.

МЕТОД ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ
5
Пластичные материалы
L T
Хрупкие материалы
nT- коэффициент запаса L B nB- коэффициент запаса
Условие
прочности:
по пределу текучести
max
Т
nТ
по пределу прочности
Условие
прочности:
max
B
nB
Величины коэффициентов запаса nT и nB устанавливаются нормами
проектирования:
nT 1,5 2,5
nв 2,5 5,0
Для материалов, неодинаково ведущих себя на растяжение и на сжатие,
условие прочности по допускаемым напряжениям выглядит так:
max р p
для конструкций,
работающих на растяжение
max с с
для конструкций,
работающих на сжатие

6.

МЕТОД ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ
6
Пример
При центральном растяжении-сжатии условие
прочности, в зависимости от исходных данных,
можно записать так:
N max
max
F
- при постоянной площади поперечного сечения
N
max
Fmin
- при постоянной нормальной силе
Аналогично расчетам на прочность по нормальным
напряжениям, проводятся расчеты на прочность по
касательным напряжениям.
Условие прочности:
max

7.

МЕТОД ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
7
Предельным называется такое состояние конструкции, при
котором ее дальнейшая эксплуатация не возможна.
В
«Строительных
нормах
и
правилах»
устанавливаются 3 группы предельных состояний:
(СНиП)
1 группа
–
определяется потерей несущей способности,
т.е. потерей прочности или устойчивости;
2 группа
–
определяется возникновением чрезмерно
больших деформаций или колебаний;
3 группа
–
определяется возникновением и развитием
трещин и других повреждений.

8.

МЕТОД ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
8
При проведении расчетов по предельным
учитываются следующие коэффициенты:
• γf – коэффициент надежности по нагрузке
Учитывает возможное увеличение нагрузки
нормативным значением, приведенным в СНиП.
по
состояниям
сравнению
с
ее
Расчетная нагрузка определяется по формуле:
Pp Pн f
Pн – нормативная нагрузка,
γf = 1,05÷1,3 – учет собственного веса как постоянной нагрузки,
γf = 1,05÷1,4 – учет временной нагрузки (снеговой, ветровой).

9.

МЕТОД ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
9
• γm – коэффициент надежности по материалу
Учитывает возможное уменьшение нормативного сопротивления Rн по
сравнению с данными испытаний на образцах.
Расчетное сопротивление материалов определяется по формуле:
R
Rн
m
Rн = σТ для пластичных материалов
Rн = σВ для хрупких материалов
γm – справочная величина. Для стали γm = 1,025÷1,15.

10.

МЕТОД ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
10
• γс – коэффициент условий работы
Зависит от вида конструкции и условий ее эксплуатации.
γс = 0,75÷1,0.
Проверку по нормальным и касательным напряжениям проводят по
формулам:
max c R
или
max c Rc
Rc ≈ 0,6R – расчетное сопротивление материала при сдвиге.
Для стали R = σТ

11.

МЕТОД РАЗРУШАЮЩИХ НАГРУЗОК
11
Пластичные материалы
Хрупкие материалы
Разрушающей считается
нагрузка, при которой в
конструкции
возникают
значительные пластические
деформации, и она не
способна
воспринимать
дальнейшее
увеличение
нагрузки.
Разрушающей считается
нагрузка, при которой хотя
бы в одном из элементов
конструкции
возникают
напряжения, равные σВ.

12.

НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИ
РАСТЯЖЕНИИ-СЖАТИИ
12
Рассмотрим стержень, нагруженный
растягивающей
силой
N,
в
наклонном сечении n1 – n1.
Согласно методу сечений, отбросим
верхнюю часть стержня, заменив ее
действие усилием p, равномерно
распределенным
по
площади
наклонного сечения.
0 против хода
часовой стрелки
р
n1
n
n0
n1
N
0
n0
n1
n1
n0
N
Площадь наклонного сечения n – n определим по формуле: F
1
1
F
cos
где F – площадь сечения n0 – n0.
Нормальная сила N определяется по формуле: N pF
Тогда
N N cos
p
cos
F
F

13.

НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИ
РАСТЯЖЕНИИ-СЖАТИИ
13
Определим нормальные σα и касательные τα напряжения в наклонном
сечении n1 – n1 :
р
σα = p cos cos cos cos
2
sin 2
τα = p sin sin cos
2
т.к. 2 sin cos sin 2
Итак, получено:
cos
2
С
внутренняя
нормаль
sin 2
2

14.

НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИ
РАСТЯЖЕНИИ-СЖАТИИ
14
Правила знаков
σα > 0, если действует от сечения (при растяжении);
σα < 0, если действует к сечению (при сжатии);
τα > 0, если поворачивается относительно точки С,
лежащей на внутренней нормали, по часовой стрелке;
τα < 0, если поворачивается относительно точки С,
лежащей на внутренней нормали, против часовой
стрелки.

15.

НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИ
РАСТЯЖЕНИИ-СЖАТИИ
15
Следствие:
σα = max при = 0 , т.к. сos0 = 1 ;
τα = max при = 45 , т.к. sin90 = 1.
Вывод:
максимальные касательные напряжения возникают
на площадках, расположенных под углом 45 к
нормали поперечного сечения стержня.
Пример: разрушение чугунного образца происходит по
площадкам
максимальных
касательных
напряжений.

16.

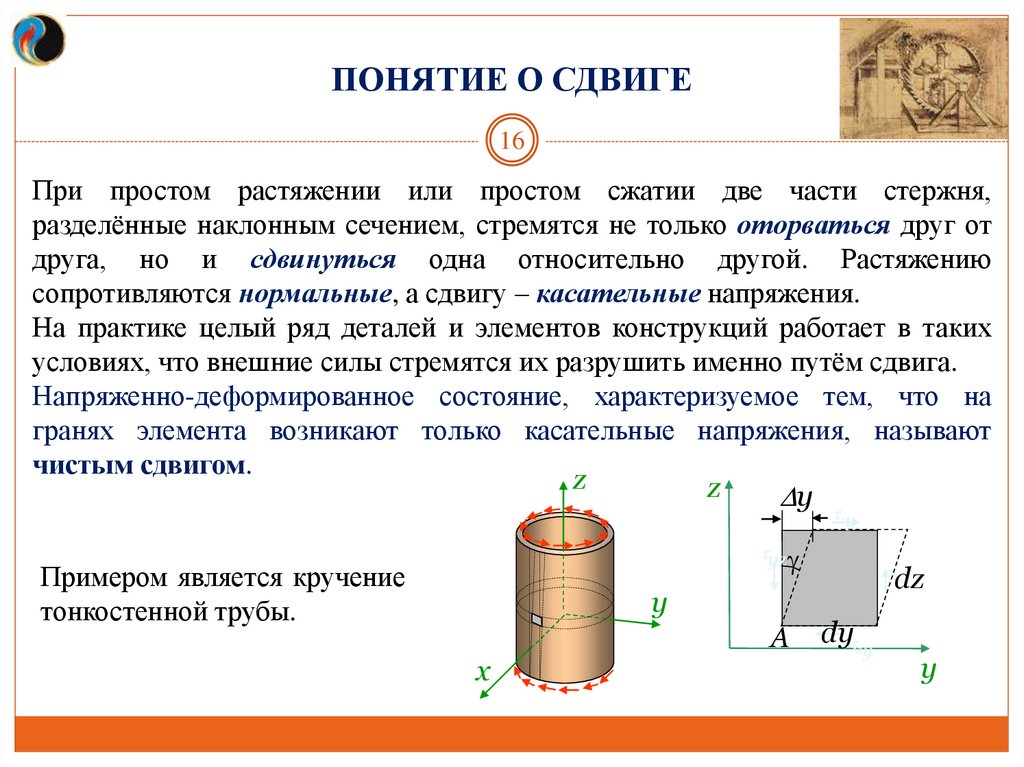
ПОНЯТИЕ О СДВИГЕ
16
При простом растяжении или простом сжатии две части стержня,
разделённые наклонным сечением, стремятся не только оторваться друг от
друга, но и сдвинуться одна относительно другой. Растяжению
сопротивляются нормальные, а сдвигу – касательные напряжения.
На практике целый ряд деталей и элементов конструкций работает в таких
условиях, что внешние силы стремятся их разрушить именно путём сдвига.
Напряженно-деформированное состояние, характеризуемое тем, что на
гранях элемента возникают только касательные напряжения, называют
чистым сдвигом.
z
z
y
z
yz
Примером является кручение
тонкостенной трубы.
y
A
x
y
dz
yz
dy zy
y

17.

КРУЧЕНИЕ
17
Кручением называется такой вид нагружения бруса, при котором в его
поперечном сечении возникает только один внутренний силовой фактор,
отличный от нуля, крутящий момент Mz или Мкр.
Mz
При действии разнонаправленных крутящих
моментов одинаковой величины в противоMz
положных торцах вала, он будет закручиваться,
сечения
вала
будут
поворачиваться
относительно друг друга, а длина вала будет
оставаться неизменной.
Положительным считается крутящий момент, направленный против часовой
стрелки, если смотреть на сечение со стороны внешней нормали.
Правило знаков для крутящего момента условно (в отличие от правила знаков
при растяжении-сжатии), т.к. материал бруса одинаково ведет себя при
кручении в разных направлениях.

18.

ДИАГРАММА КРУЧЕНИЯ
18
Основные характерные точки:
τ
τ
До напряжения ПЦ, называемого
пределом пропорциональности при
сдвиге справедлива линейная зависимость
(закон Гука при сдвиге):
τmax
G
τ
τ
Т
ПЦ
γ – угол сдвига
α
γ
(угловая
деформация)
tg
G – модуль сдвига (модуль упругости второго
рода), справочная величина, неизменная и
постоянная для каждого материала.
G = tg
y
dy
рад
G Н2 Па
м

19.

ДИАГРАММА КРУЧЕНИЯ
19
τ – касательное напряжение, при котором угол сдвига возрастает при
Т
постоянном напряжении, называется пределом текучести при сдвиге.
τmax – максимальное напряжение, выдерживаемое образцом до
разрушения.

20.

СВЯЗЬ МЕЖДУ МОДУЛЕМ СДВИГА И МОДУЛЕМ
УПРУГОСТИ ПРИ РАСТЯЖЕНИИ
20
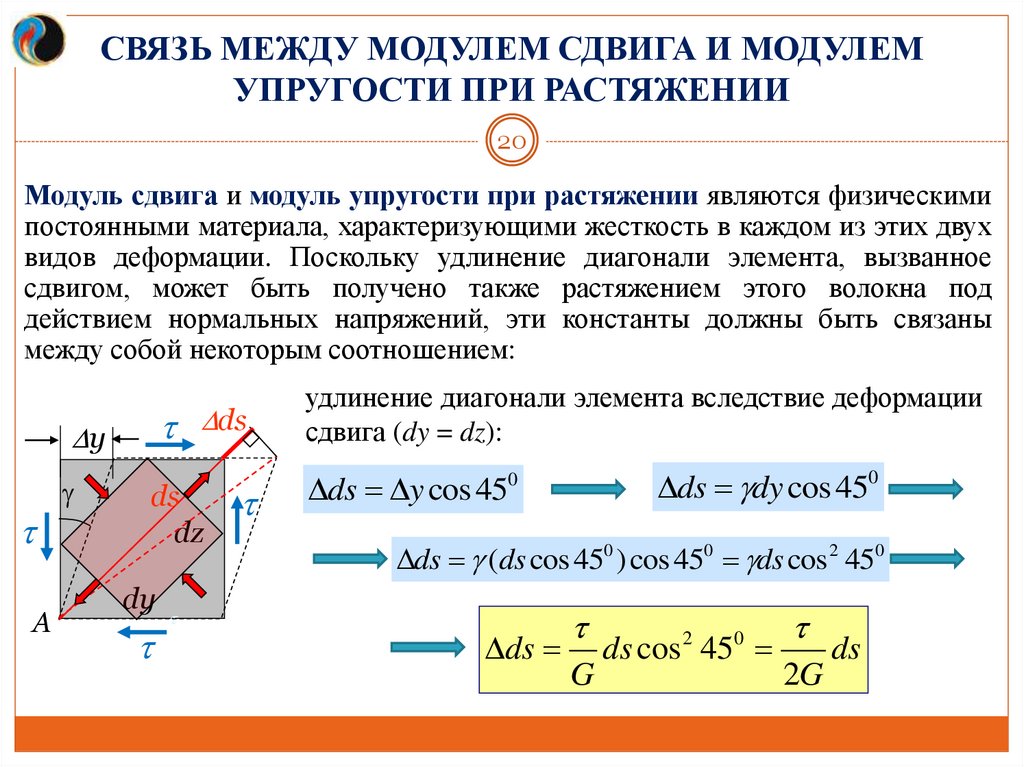
Модуль сдвига и модуль упругости при растяжении являются физическими
постоянными материала, характеризующими жесткость в каждом из этих двух
видов деформации. Поскольку удлинение диагонали элемента, вызванное
сдвигом, может быть получено также растяжением этого волокна под
действием нормальных напряжений, эти константы должны быть связаны
между собой некоторым соотношением:
ds
y
A
ds
dz
dy
удлинение диагонали элемента вследствие деформации
сдвига (dy = dz):
ds dy cos 450
ds y cos 450
ds (ds cos 450 ) cos 450 ds cos 2 450
ds
G
ds cos 2 450
2G
ds

21.

СВЯЗЬ МЕЖДУ МОДУЛЕМ СДВИГА И МОДУЛЕМ
УПРУГОСТИ ПРИ РАСТЯЖЕНИИ
21
Удлинение диагонали элемента вследствие деформации растяжения (σ1 = ,
σ2 = – ):
ds 1
1
(1 )
(1 )
1
( 1 2 ) ( ( ))
ds
ds
ds
E
E
E
E
(1 )
ds ds cos 45
ds ds
ds
G
2G
E
2
0
(1 )
1
E
2G
или
E
G
2(1 )
Таким образом существует соотношение между модулем сдвига и модулем упругости при
растяжении с участием коэффициента Пуассона. Любую из этих величин можно определить,
если известны две другие.

22.

КРУЧЕНИЕ
22
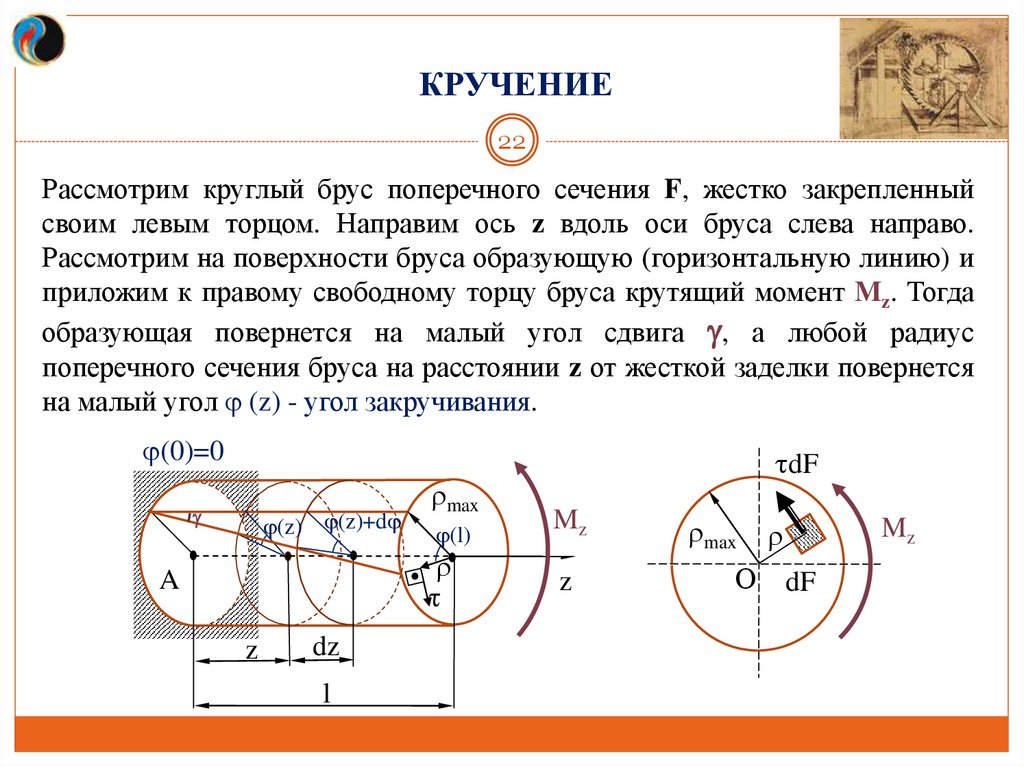
Рассмотрим круглый брус поперечного сечения F, жестко закрепленный
своим левым торцом. Направим ось z вдоль оси бруса слева направо.
Рассмотрим на поверхности бруса образующую (горизонтальную линию) и
приложим к правому свободному торцу бруса крутящий момент Mz. Тогда
образующая повернется на малый угол сдвига , а любой радиус
поперечного сечения бруса на расстоянии z от жесткой заделки повернется
на малый угол (z) - угол закручивания.
(0)=0
(z) (z)+d
max
(l)
A
z
dz
l
dF
Mz
max
z
О
Mz
dF

23.

КРУЧЕНИЕ
23
dS
d
dz
Рассмотрим бесконечно малый участок бруса длиной
dz и радиусом . В силу гипотезы о линейной
зависимости деформаций от приложенных сил,
относительный угол закручивания равен:
d ( z )
рад
const ,
dz
В силу закона Гука для кручения (сдвига) имеем:
G Gtg G
d
dz
, т.к. dS d , tg
м
dS
, 1
dz
Касательные напряжения лежат в плоскости круглого поперечного сечения
бруса и перпендикулярны его радиусу
Крутящий момент определим по формуле:
d M z
d 2
d
d
2
M z dF G
dF G
dF G J p ,
dz GJ p
dz
dz F
dz
F
F

24.

КРУЧЕНИЕ
24
Жесткостью сечения круглого бруса при кручении называется величина GJ p
Размерность: