Похожие презентации:
Расчеты на прочность при прямом плоском изгибе
1.
РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИПРЯМОМ ПЛОСКОМ ИЗГИБЕ.
Изгибом называется такой простой вид деформации, при котором в поперечном сечении стержня возникают два внутренних
усилия – изгибающий момент и поперечная сила, остальные внутренние усилия отсутствуют.
Стержни, работающие преимущественно на изгиб, называются
балками. В отличие от осевого растяжения-сжатия и кручения, изгиб представляет собой такую деформацию, при которой происходит искривление оси первоначально прямого бруса.
В строительных конструкциях часто встречаются балки, поперечое сечение которых имеет хотя бы одну ось симметрии.
2.
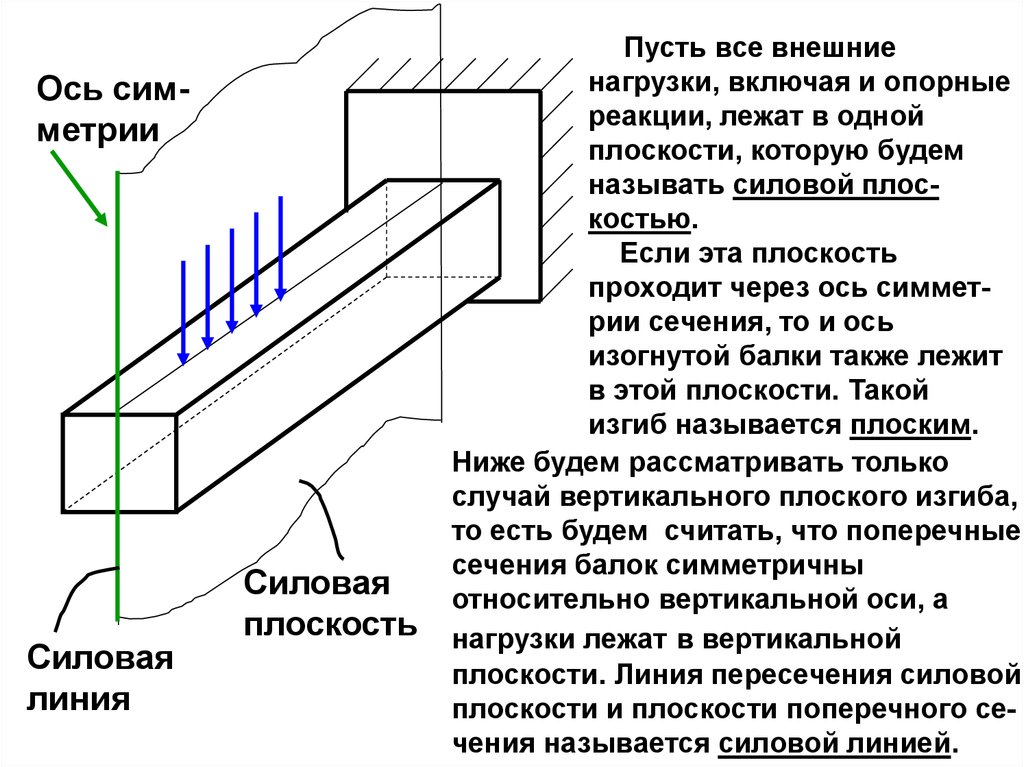
Ось симметрииСиловая
линия
Силовая
плоскость
Пусть все внешние
нагрузки, включая и опорные
реакции, лежат в одной
плоскости, которую будем
называть силовой плоскостью.
Если эта плоскость
проходит через ось симметрии сечения, то и ось
изогнутой балки также лежит
в этой плоскости. Такой
изгиб называется плоским.
Ниже будем рассматривать только
случай вертикального плоского изгиба,
то есть будем считать, что поперечные
сечения балок симметричны
относительно вертикальной оси, а
нагрузки лежат в вертикальной
плоскости. Линия пересечения силовой
плоскости и плоскости поперечного сечения называется силовой линией.
3.
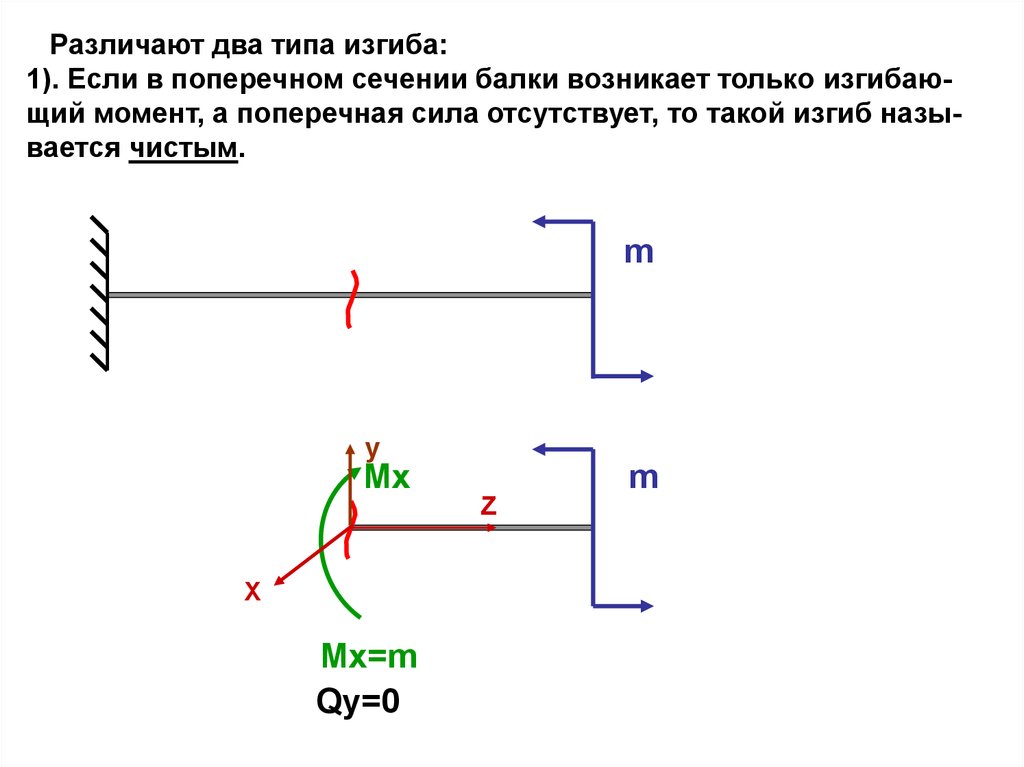
Различают два типа изгиба:1). Если в поперечном сечении балки возникает только изгибающий момент, а поперечная сила отсутствует, то такой изгиб называется чистым.
m
y
Mx
m
Z
X
Mx=m
Qy=0
4.
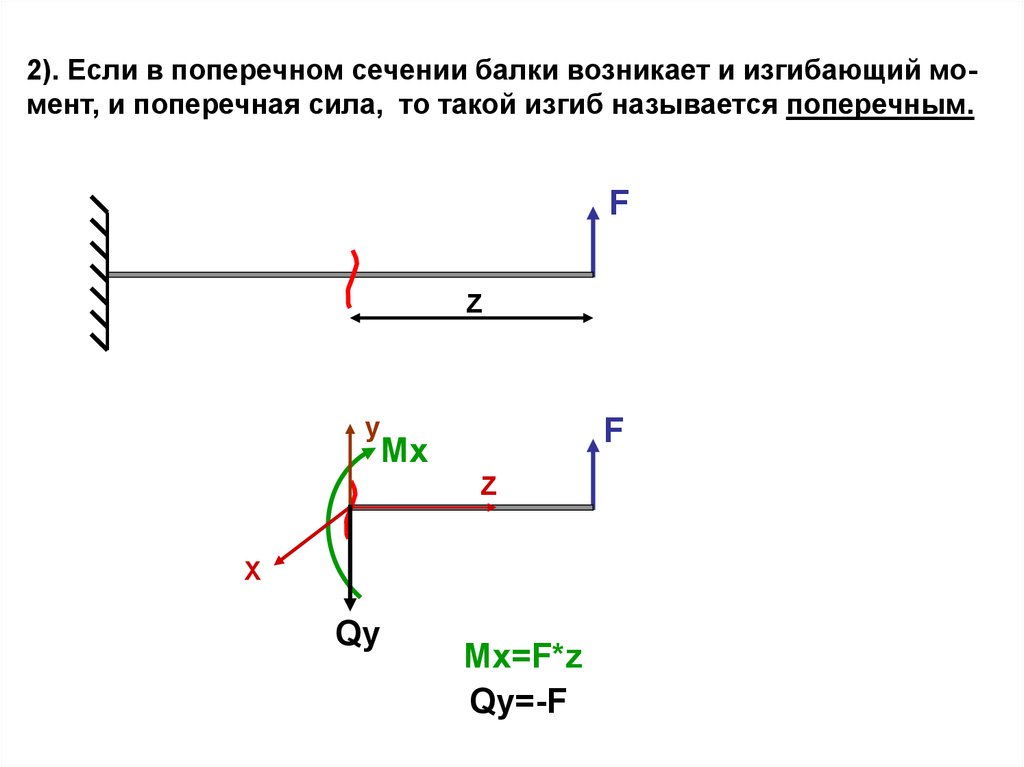
2). Если в поперечном сечении балки возникает и изгибающий момент, и поперечная сила, то такой изгиб называется поперечным.F
Z
y
F
Mx
Z
X
Qy
Mx=F*z
Qy=-F
5.
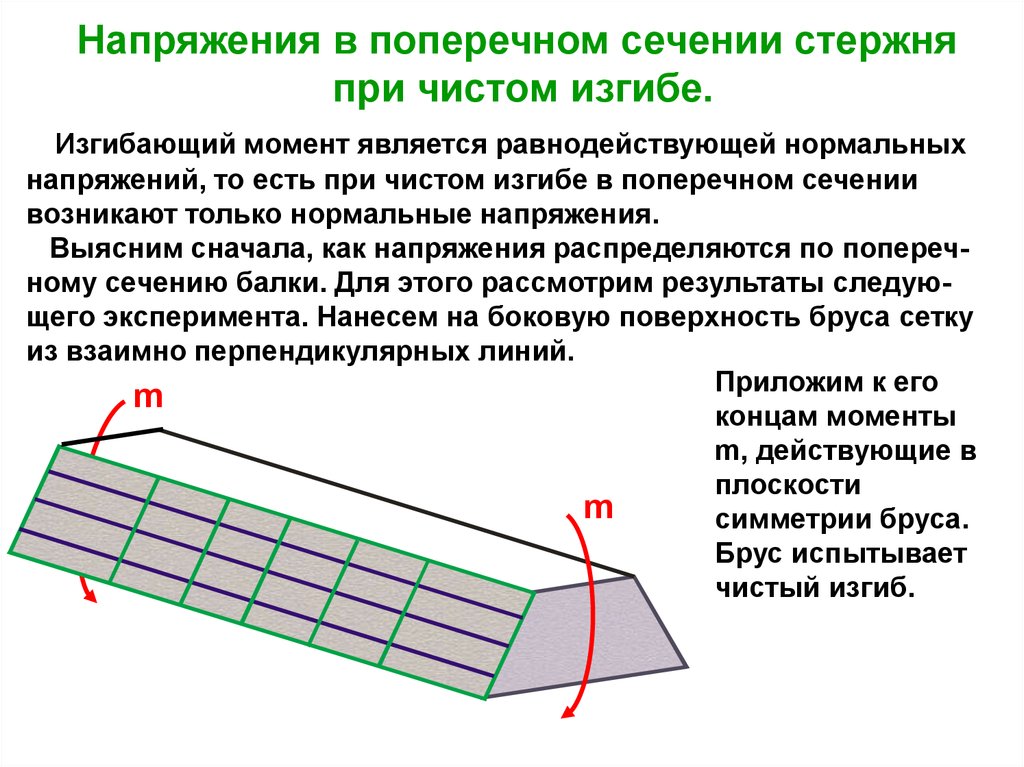
Напряжения в поперечном сечении стержняпри чистом изгибе.
Изгибающий момент является равнодействующей нормальных
напряжений, то есть при чистом изгибе в поперечном сечении
возникают только нормальные напряжения.
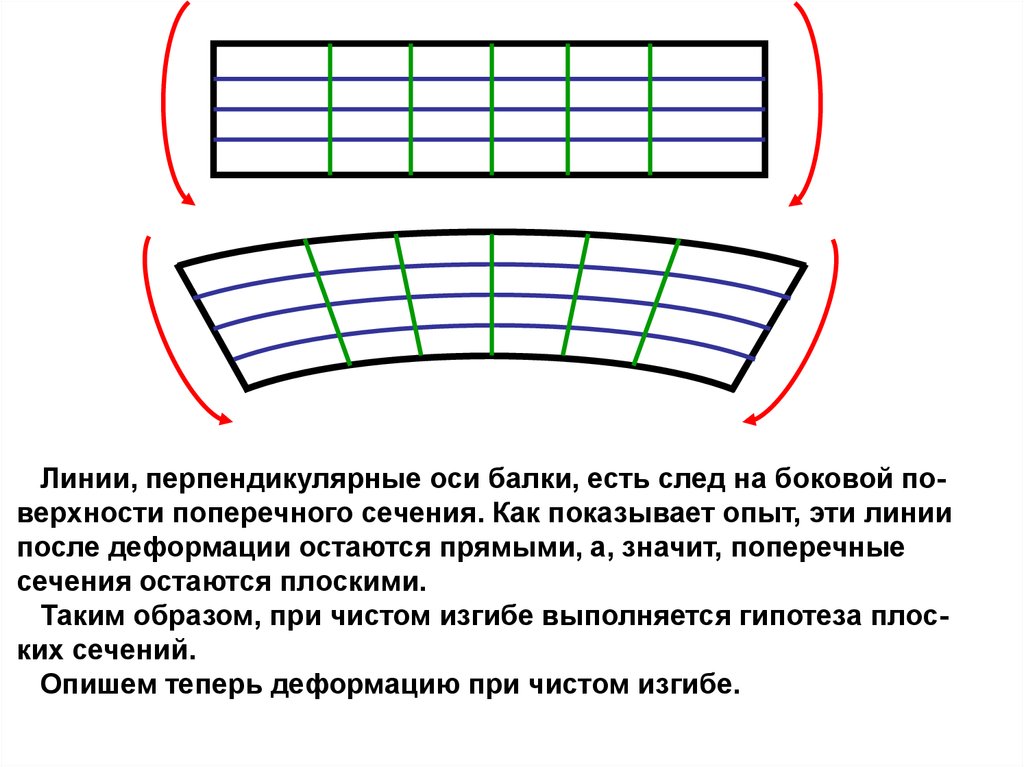
Выясним сначала, как напряжения распределяются по поперечному сечению балки. Для этого рассмотрим результаты следующего эксперимента. Нанесем на боковую поверхность бруса сетку
из взаимно перпендикулярных линий.
Приложим к его
m
концам моменты
m, действующие в
плоскости
m
симметрии бруса.
Брус испытывает
чистый изгиб.
6.
При приложении моментов брус изгибается, при этом линии, параллельные оси балки, искривляются, удлиняясь вверху и укорачиваясь внизу. Расстояние же между ними не меняется. Поэтому приизгибе выполняется следующая гипотеза: «Продольные волокна не
давят друг на друга».
7.
Линии, перпендикулярные оси балки, есть след на боковой поверхности поперечного сечения. Как показывает опыт, эти линиипосле деформации остаются прямыми, а, значит, поперечные
сечения остаются плоскими.
Таким образом, при чистом изгибе выполняется гипотеза плоских сечений.
Опишем теперь деформацию при чистом изгибе.
8.
adz
e
c
d
e’
a
c
d’
dΘ
О
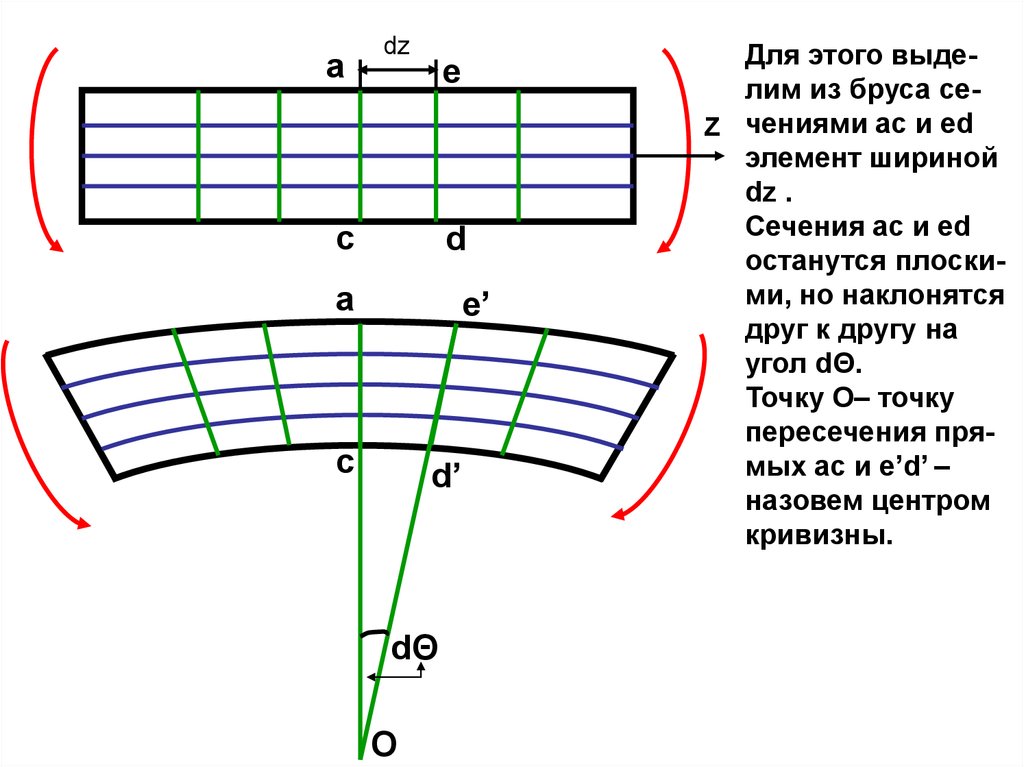
Для этого выделим из бруса сеZ чениями ac и ed
элемент шириной
dz .
Сечения ac и ed
останутся плоскими, но наклонятся
друг к другу на
угол dΘ.
Точку О– точку
пересечения прямых ac и e’d’ –
назовем центром
кривизны.
9.
YX
dz
e
a
L
c
ρ
О
Z
K
н.слой
d’
e’
d
Так как верхние волокна удлиняются, а нижние укорачиваются, то обязательно существует слой LK, волокна которого не изменяют свою длину.
Этот слой называется
нейтральным.
Расстояние от этого слоя до
т.О назовем радиусом кривизны нейтрального слоя ρ.
Систему координат выберем
так, что ее начало находится в
т.L, оси Z и X лежат в нейтральном слое, а ось Y –
вертикальна.
10.
XY
dz
c
n’
n
y
L
e’
e
a
m
н.слой
d’
K
d
ρ
Z
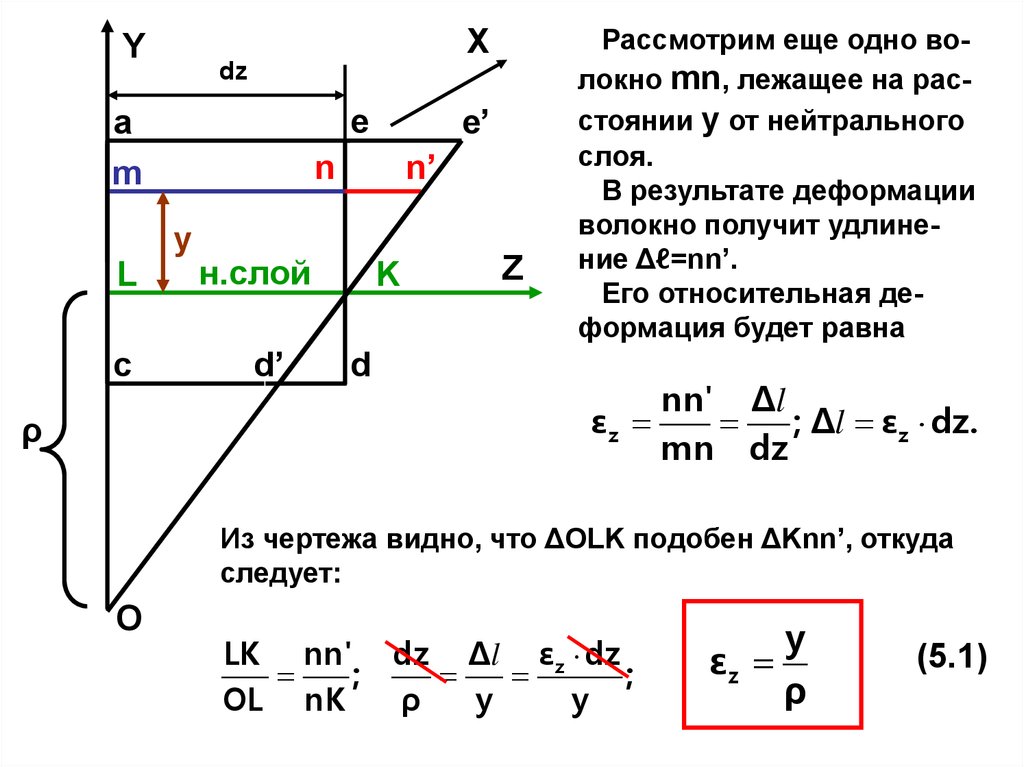
Рассмотрим еще одно волокно mn, лежащее на расстоянии y от нейтрального
слоя.
В результате деформации
волокно получит удлинение Δℓ=nn’.
Его относительная деформация будет равна
nn' Δl
εz
; Δl ε z dz.
mn dz
Из чертежа видно, что ΔOLK подобен ΔKnn’, откуда
следует:
О
LK nn'
;
OL nK
dz Δl ε z dz
;
ρ
y
y
y
εz
ρ
(5.1)
11.
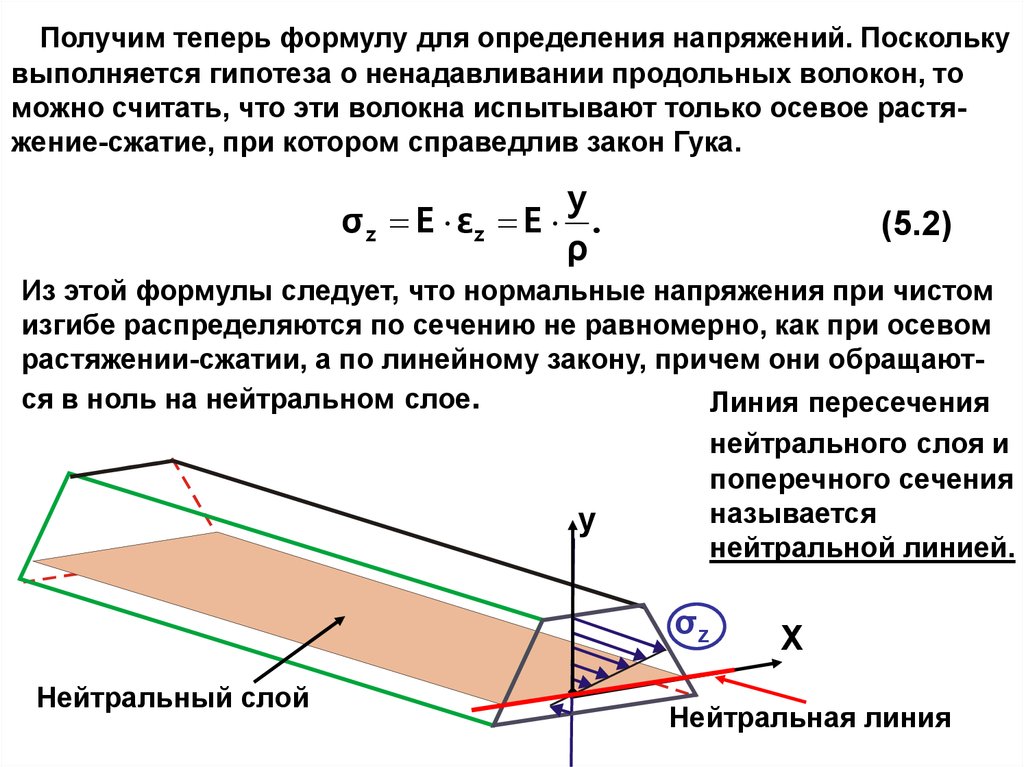
Получим теперь формулу для определения напряжений. Посколькувыполняется гипотеза о ненадавливании продольных волокон, то
можно считать, что эти волокна испытывают только осевое растяжение-сжатие, при котором справедлив закон Гука.
y
σ z E εz E .
ρ
(5.2)
Из этой формулы следует, что нормальные напряжения при чистом
изгибе распределяются по сечению не равномерно, как при осевом
растяжении-сжатии, а по линейному закону, причем они обращаются в ноль на нейтральном слое.
Линия пересечения
нейтрального слоя и
поперечного сечения
называется
нейтральной линией.
y
σz
Нейтральный слой
X
Нейтральная линия
12.
Формула (5.2) неудобна для работы, так как в общем случае радиус нейтрального слоя ρ неизвестен. Получим ее в другом виде.Для этого выпишем из формул (1.1) те, в которые входит нормальное напряжение σz.
N=
σ z dA
(*)
A
Mx = σ z y dA
(**)
My = σ z x dA
(***)
A
A
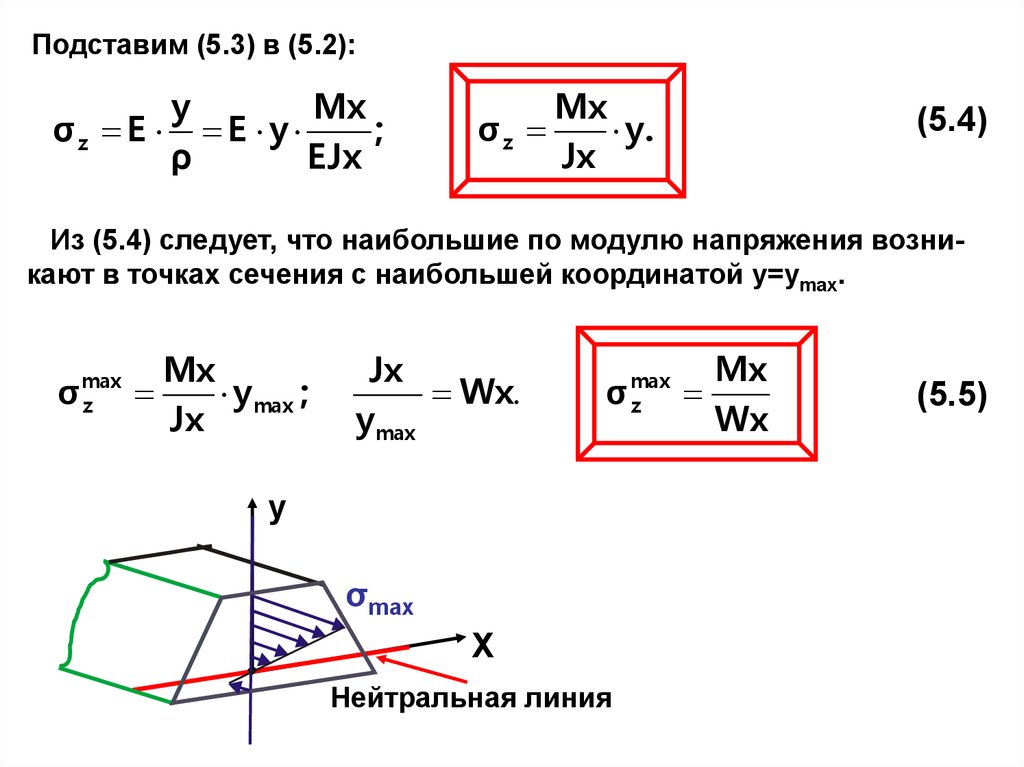
Подставим формулу (5.2) в формулу (**):
y
E
2
E
y
dA
y
dA;
Mx = σ z y dA ρ
ρA
A
A
EJx
Mx
.
ρ
Jx
Отсюда получаем
1 Mx
ρ EJx
(5.3)
13.
Подставим (5.3) в (5.2):y
Mx
σz E E y
;
ρ
EJx
σz
Mx
y.
Jx
(5.4)
Из (5.4) следует, что наибольшие по модулю напряжения возникают в точках сечения с наибольшей координатой y=ymax.
σ
max
z
Mx
y max ;
Jx
Jx
Wx.
y max
σ
y
σmax
X
Нейтральная линия
max
z
Mx
Wx
(5.5)
14.
yИз формулы (5.4) слеНейтральная дует, что величина напрялиния
жений зависит от координаты y, то есть зависит от
X
выбора системы коордиC
нат. Выясним сначала, как
определить положение
нейтральной линии. Для этого возьмем формулу (*) и подставим
в нее выражение (5.2):
E
y
E
N = σ z dA E dA y dA; N = Sx 0,
ρ
ρ
ρA
A
A
Sx
так как при изгибе продольная сила N не возникает. Из последнего
выражения следует, что для этого должен быть равен нулю статический момент Sx . Статический же момент обращается в нуль относительно центральной оси. Отсюда следует, что ось X, то есть нейтральная линия сечения обязательно проходит через центр тяжести.
15.
yX
C
Выясним теперь местоположение оси Y. Для
этого возьмем формулу
(***) и подставим в нее
выражение (5.2):
Ось симметрии
y
E
E
My = σ z x dA E x dA y x dA; My Jxy 0,
ρ
ρA
ρ
A
A
Jxy
так как при вертикальном плоском изгибе изгибающий момент My не
возникает. Из последнего выражения следует, что для этого должен
быть равен нулю центробежный момент инерции Jxy. Центробежный же момент обращается в нуль относительно главных осей. Известно, что если сечение имеет ось симметрии и одна из кординатных осей с ней совпадает, то эти оси будут главными. Отсюда следует, что вертикальная ось Y должна совпадать с осью симметрии
сечения.
16.
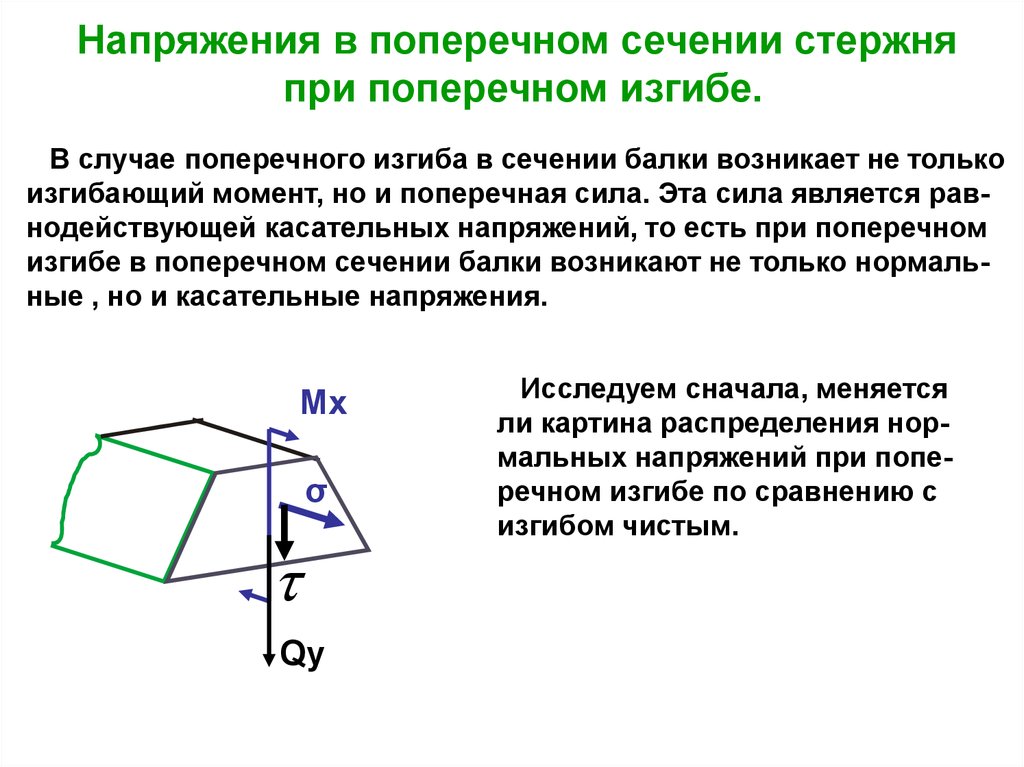
Напряжения в поперечном сечении стержняпри поперечном изгибе.
В случае поперечного изгиба в сечении балки возникает не только
изгибающий момент, но и поперечная сила. Эта сила является равнодействующей касательных напряжений, то есть при поперечном
изгибе в поперечном сечении балки возникают не только нормальные , но и касательные напряжения.
Mx
σ
Qy
Исследуем сначала, меняется
ли картина распределения нормальных напряжений при поперечном изгибе по сравнению с
изгибом чистым.
17.
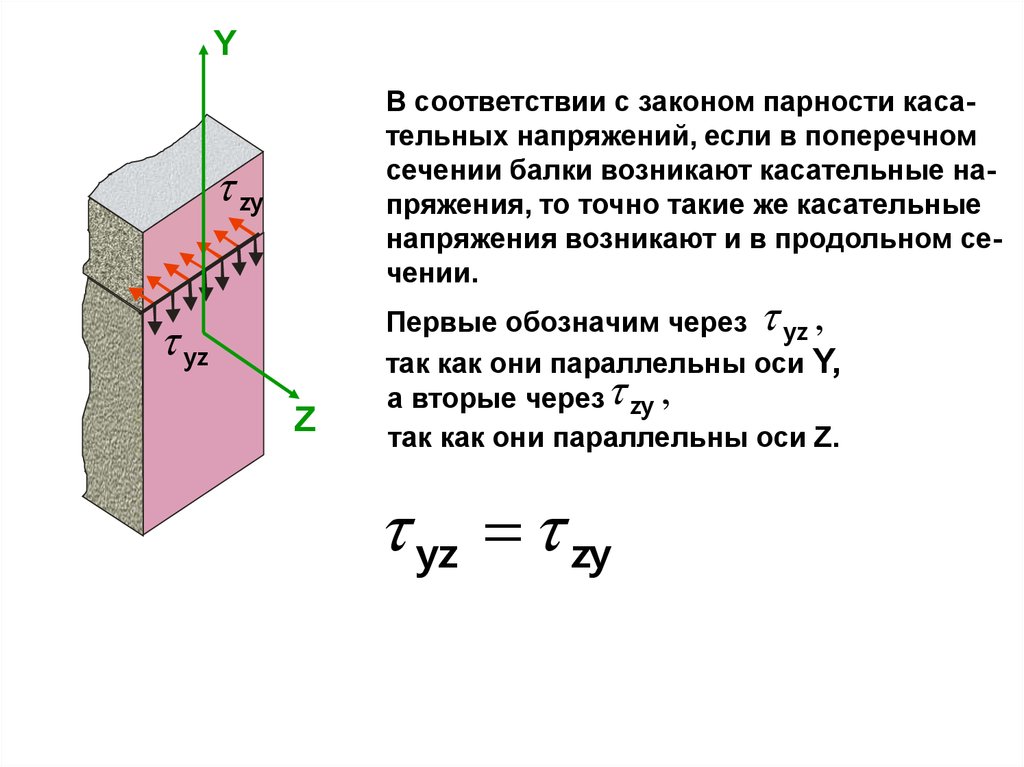
YВ соответствии с законом парности касательных напряжений, если в поперечном
сечении балки возникают касательные напряжения, то точно такие же касательные
напряжения возникают и в продольном сечении.
zy
yz
Z
Первые обозначим через yz ,
так как они параллельны оси Y,
а вторые через zy ,
так как они параллельны оси Z.
yz zy
18.
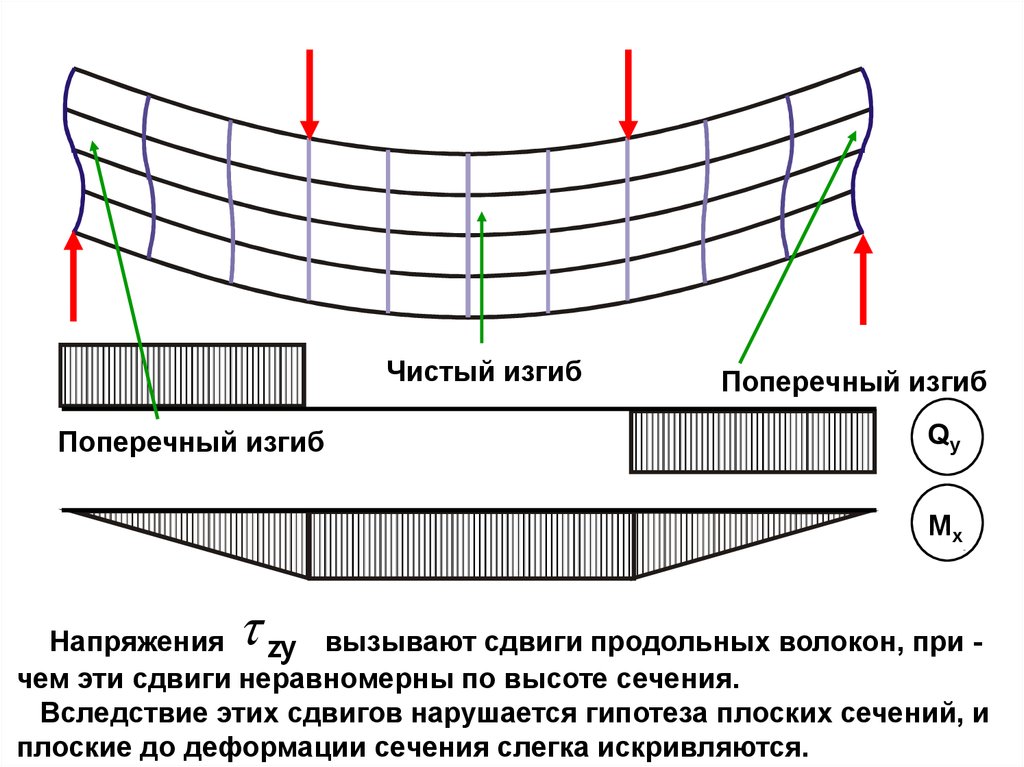
Чистый изгибПоперечный изгиб
Поперечный изгиб
Qy
Mx
Напряжения zy вызывают сдвиги продольных волокон, при чем эти сдвиги неравномерны по высоте сечения.
Вследствие этих сдвигов нарушается гипотеза плоских сечений, и
плоские до деформации сечения слегка искривляются.
19.
Экспериментальные и теоретические исследования показывают,что величина нормальных напряжений при этом хотя и меняется,
но очень незначительно. Поэтому влиянием сдвигов на закон распределения нормальных напряжений пренебрегают и используют
для их определения те же формулы (5.4), (5.5), что и при чистом
изгибе.
Получим теперь формулу для определения касательных напряжений.
20.
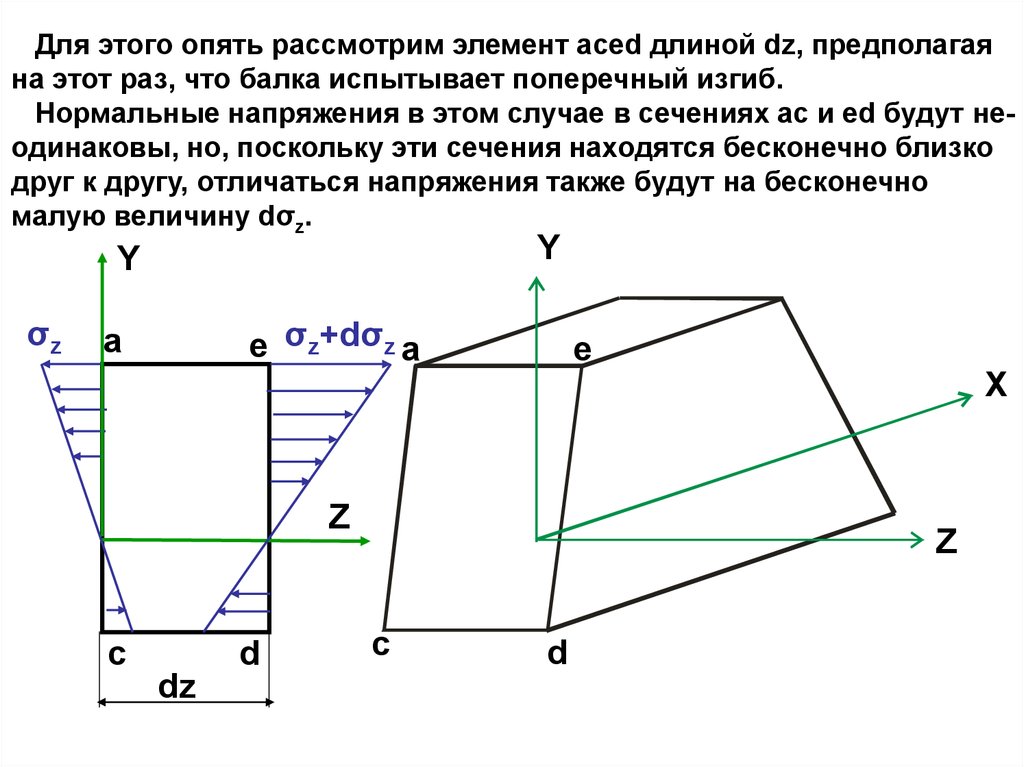
Для этого опять рассмотрим элемент aced длиной dz, предполагаяна этот раз, что балка испытывает поперечный изгиб.
Нормальные напряжения в этом случае в сечениях ac и ed будут неодинаковы, но, поскольку эти сечения находятся бесконечно близко
друг к другу, отличаться напряжения также будут на бесконечно
малую величину dσz.
Y
Y
σz
e σz+dσz a
a
e
X
Z
c
d
dz
Z
c
d
21.
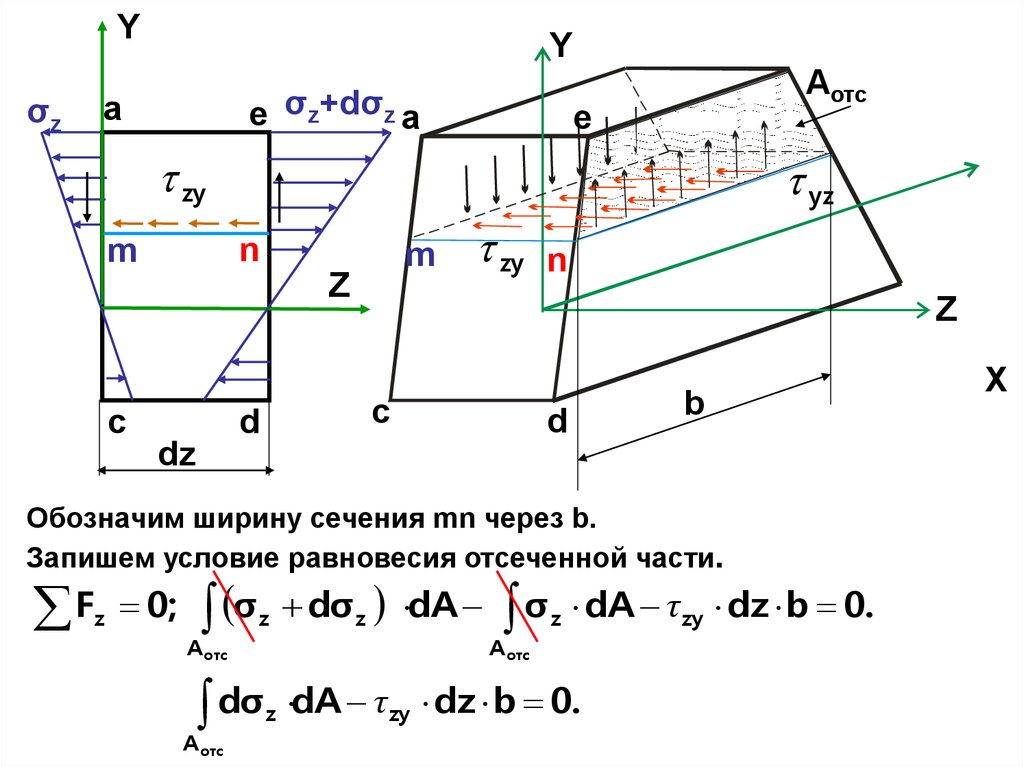
Выделим теперь из элемента aced элемент amne, проведя продольное сечение mn.Покажем действующие на его гранях касательные напряжения
yz zy . Будем при этом предполагать, что эти касательные напряжения по всей ширине сечения, то есть вдоль оси X, распределены равномерно, а направление yz совпадают с направлением поперечной силы Qy, возникающей в сечении.
Часть поперечного сечения, лежащую выше проведенного сечения
mn, назовем отсеченной, а ее площадь обозначим через Аотс.
Y
Y
σz
e σz+dσz a
a
e
zy
m
X
yz
n
m
Z
c
Aотс
d
zy
n
Z
c
d
22.
Yσz
Y
e σz+dσz a
a
Aотс
e
zy
yz
n
m
m
Z
c
zy
Z
c
d
n
b
d
dz
Обозначим ширину сечения mn через b.
Запишем условие равновесия отсеченной части.
F
z
0;
σ
z
A отс
dσ
A отс
dσ z dA
σ
z
dA τ zy dz b 0.
A отс
z
dA τ zy dz b 0.
X
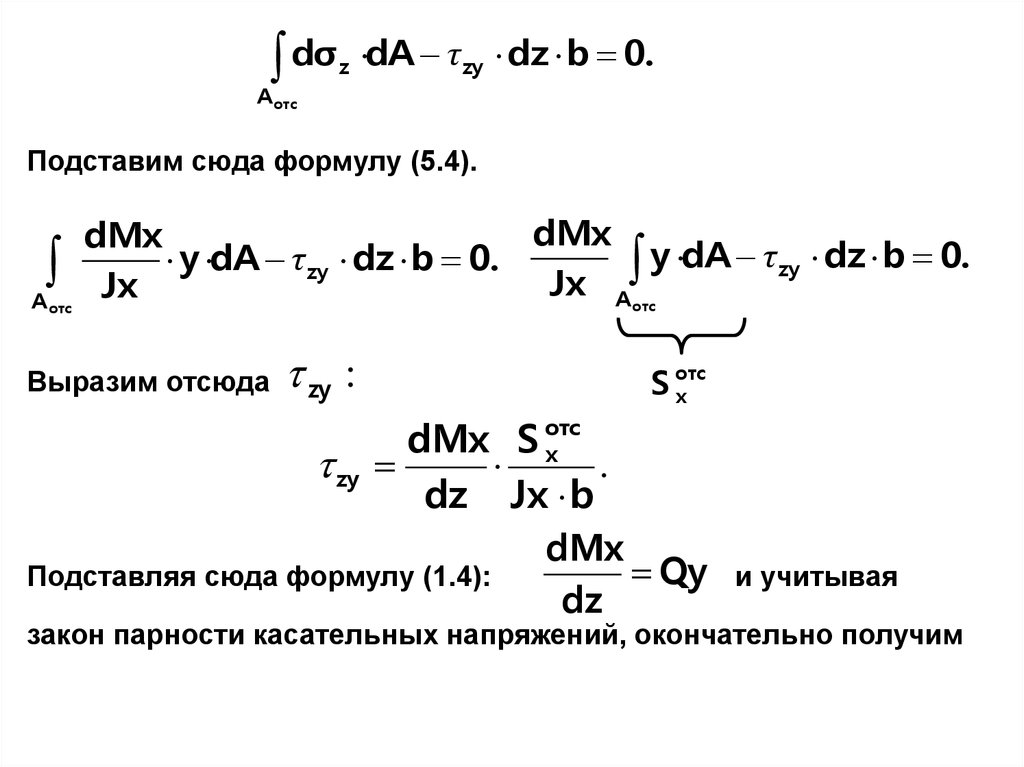
23.
dσz
dA τ zy dz b 0.
A отс
Подставим сюда формулу (5.4).
A отс
dMx
dMx
y dA τ zy dz b 0.
y dA τ zy dz b 0.
Jx A отс
Jx
Выразим отсюда
zy :
zy
S отс
x
dMx S отс
x .
dz Jx b
Подставляя сюда формулу (1.4):
dMx
Qy
dz
и учитывая
закон парности касательных напряжений, окончательно получим
24.
yzQy S отс
x
.
Jx b
(5.6)
Формула (5.6) называется формулой Журавского.
Здесь Qy – абсолютная величина поперечной силы в том сечении,
где вычисляются касательные напряжения;
Jx – момент инерции этого сечения относительно нейтральной линии (оси X);
b – ширина сечения на уровне рассматриваемого
волокна;
S отс
x -- статический момент относительно нейтральной
линии (оси X) отсеченной части сечения, лежащей выше
(или ниже) уровня рассматриваемого волокна.
Формула (5.6) дает только величину касательных напряжений. Направления их совпадают с направлением поперечной силы Qy.
Распределение касательных напряжений по высоте сечения существенно зависит от формы сечения.
25.
Рассмотрим несколько частных случаев. Будем предполагать, чтопоперечная сила в рассматриваемых сечениях направлена вверх.
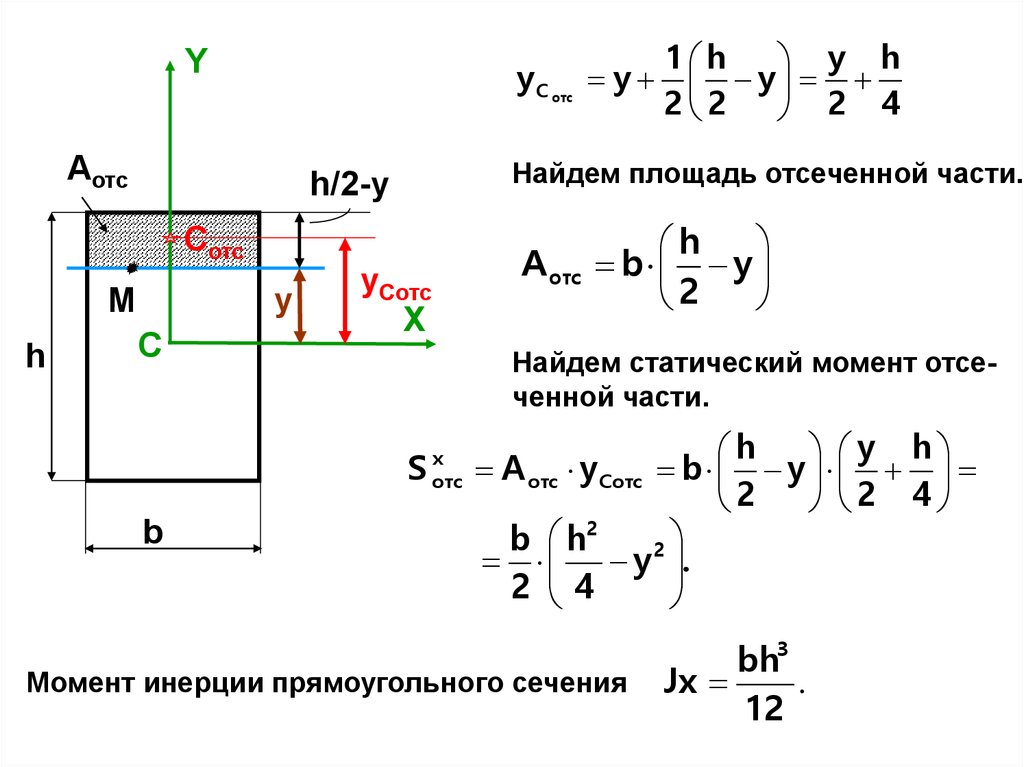
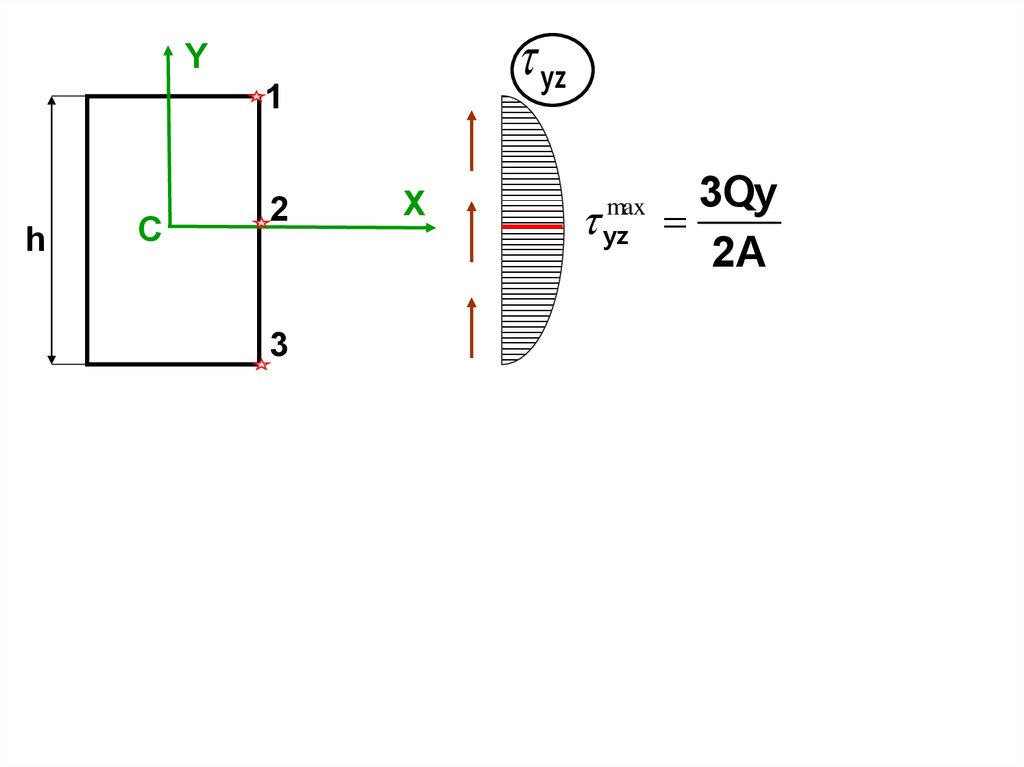
1. Сечение прямоугольной формы.
Y
Aотс
h/2-y
Cотс
y
M
h
C
b
yСотс
X
Рассмотрим прямоугольное сечение размерами h*b, проведем главную центральную систему координат CXY.
Найдем величину касательных
напряжений в произвольной т.М с
координатами (x,y).
Сначала проведем через эту точку
линию, параллельную оси X. Назовем отсеченной часть сечения, лежащую, например, выше этой линии.
Обозначим через Сотс центр тяжести отсеченной части и найдем
его координату.
y C отс y
1 h
y h
y
2 2
2 4
26.
Yy C отс y
Aотс
Найдем площадь отсеченной части.
h/2-y
Cотс
y
M
h
C
yСотс
X
А отс
h
b y
2
Найдем статический момент отсеченной части.
S
b
1 h
y h
y
2 2
2 4
x
отс
h
y h
A отс y Cотс b y
2
2 4
b h2
2
y .
2 4
Момент инерции прямоугольного сечения
bh3
Jx
.
12
27.
Подставляем все найденные величины в формулу Журавского:τ yz
b h2
2
Qy y
отс
2
2 4
Qy S x
6Qy
h
2
y .
3
3
bh
Jx b
bh 4
b
12
Это уравнение параболы. Построим ее график. Для этого найдем
значения напряжения в нескольких точках.
Y
h
C
2
3
В т.3
yz 0.
y=-h/2; yz 0.
В т.2
y=0;
В т.1
1
X
max
τ yz yz
y=h/2;
6Qy h2 3Qy 3Qy
.
3
bh 4 2bh
2A
28.
yzY
1
h
C
2
3
X
max
yz
3Qy
2A
29.
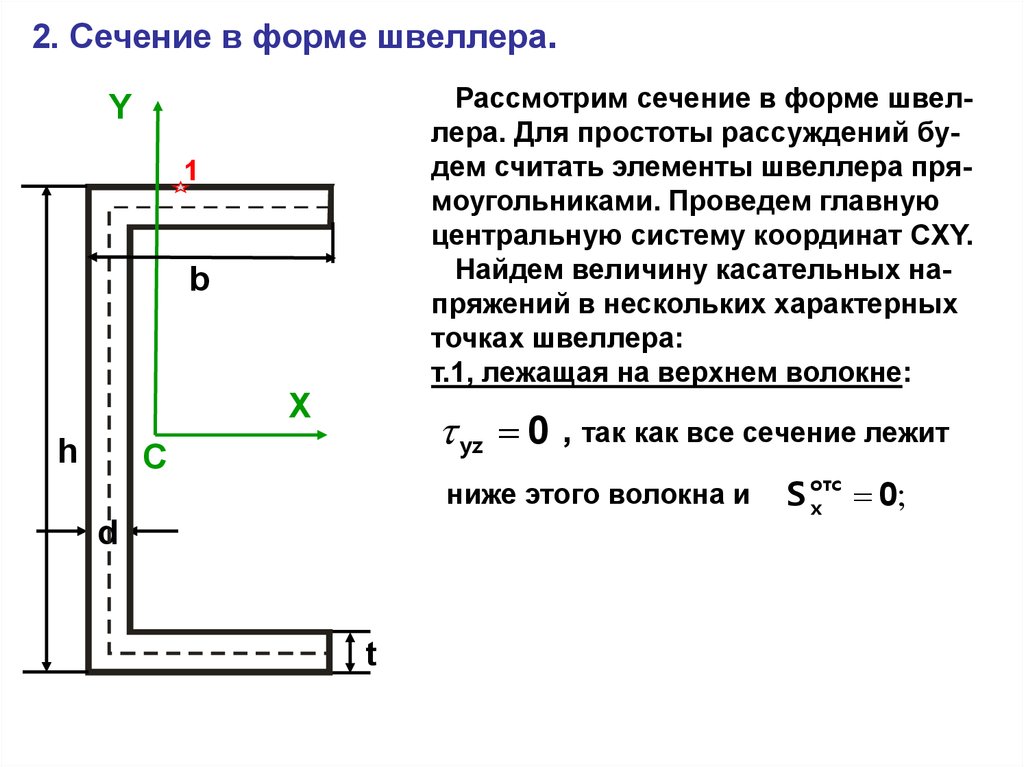
2. Сечение в форме швеллера.Рассмотрим сечение в форме швеллера. Для простоты рассуждений будем считать элементы швеллера прямоугольниками. Проведем главную
центральную систему координат CXY.
Найдем величину касательных напряжений в нескольких характерных
точках швеллера:
т.1, лежащая на верхнем волокне:
Y
1
b
X
h
yz 0 , так как все сечение лежит
C
ниже этого волокна и
d
t
S отс
0;
x
30.
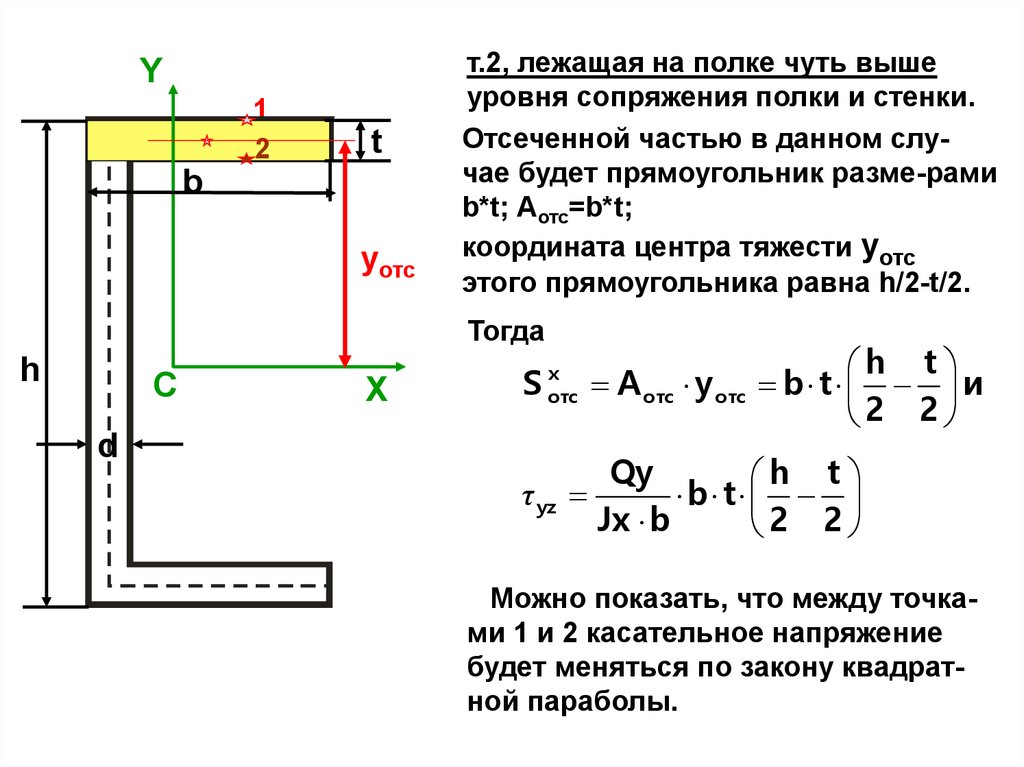
Y1
2
t
b
yотс
т.2, лежащая на полке чуть выше
уровня сопряжения полки и стенки.
Отсеченной частью в данном случае будет прямоугольник разме-рами
b*t; Аотс=b*t;
координата центра тяжести yотс
этого прямоугольника равна h/2-t/2.
Тогда
h
C
X
S
x
отс
d
τ yz
A отс y отс
h t
b t и
2 2
Qy
h t
b t
Jx b
2 2
Можно показать, что между точками 1 и 2 касательное напряжение
будет меняться по закону квадратной параболы.
31.
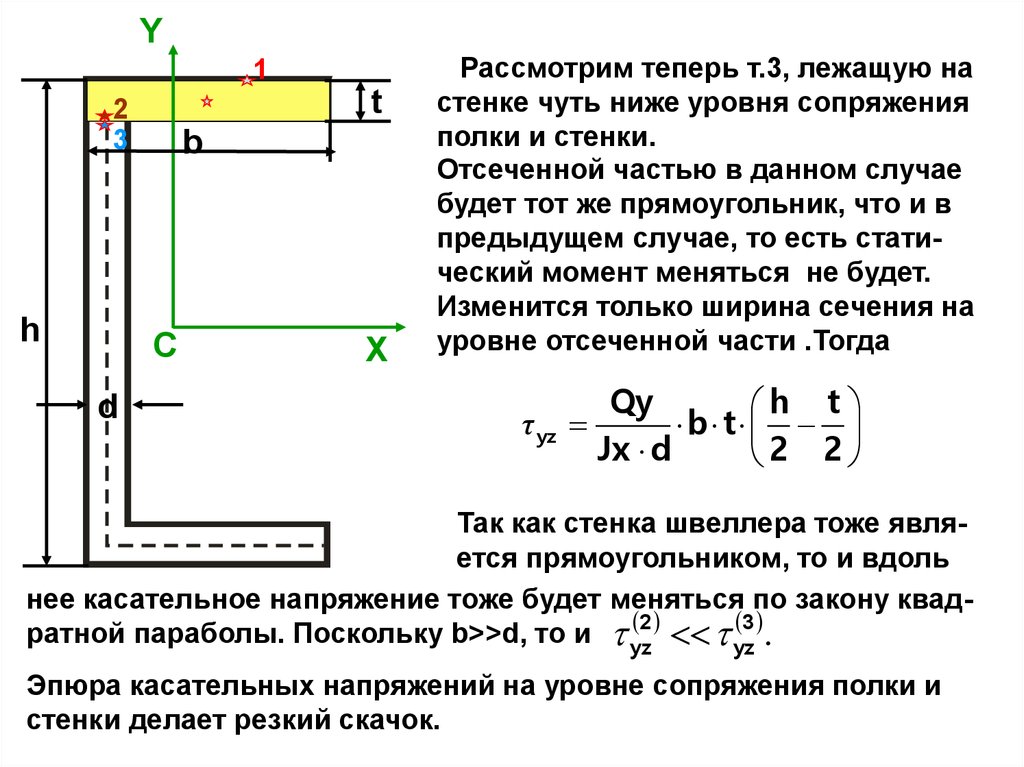
Y1
t
2
3
h
b
C
d
X
Рассмотрим теперь т.3, лежащую на
стенке чуть ниже уровня сопряжения
полки и стенки.
Отсеченной частью в данном случае
будет тот же прямоугольник, что и в
предыдущем случае, то есть статический момент меняться не будет.
Изменится только ширина сечения на
уровне отсеченной части .Тогда
τ yz
Qy
h t
b t
Jx d
2 2
Так как стенка швеллера тоже является прямоугольником, то и вдоль
нее касательное напряжение тоже будет меняться по закону квад 2
3
ратной параболы. Поскольку b>>d, то и yz
yz
.
Эпюра касательных напряжений на уровне сопряжения полки и
стенки делает резкий скачок.
32.
23
1
yz
4
Максимальные касательные напряжения возникают на нейтральной линии (т.4) и определяются по формуле:
max
τ yz
d h2
Qy (h
- t ) t b d 4
.
2Jx d
Строим эпюру
( получить
самостоятельно).
yz .
Отметим, что обычно ввиду малости касательные напряжения
yz
на полках швеллера не определяются.
33.
YZ
X
zx
p
σz
σz+dσz
n
m
s
dz
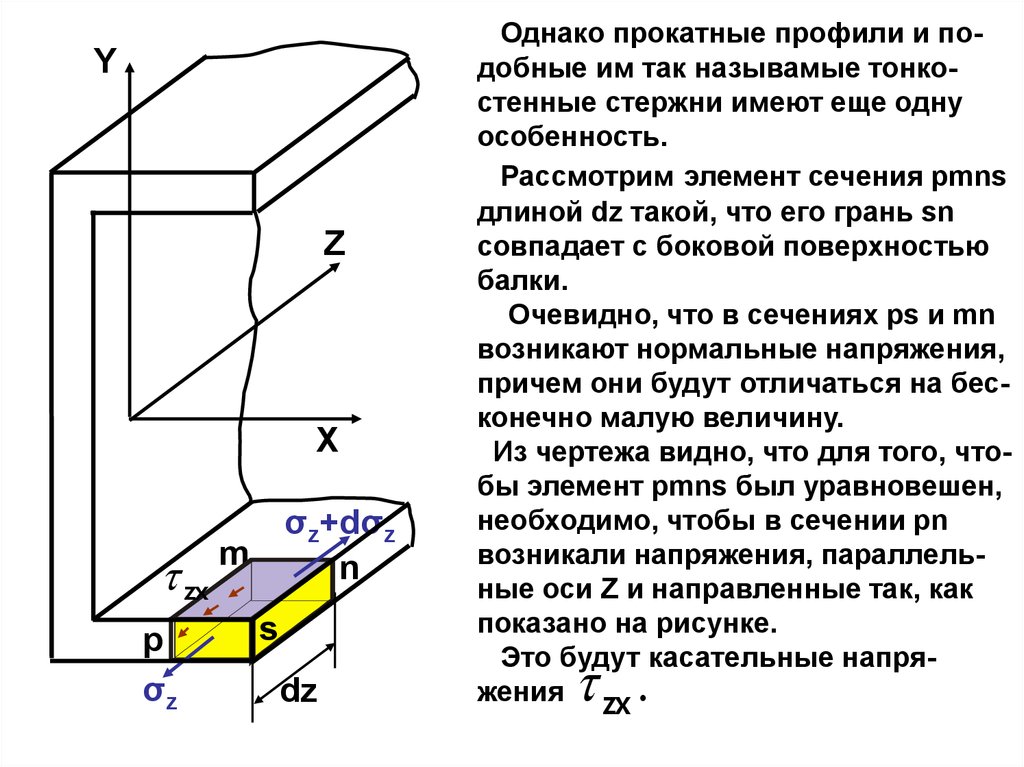
Однако прокатные профили и подобные им так называмые тонкостенные стержни имеют еще одну
особенность.
Рассмотрим элемент сечения pmns
длиной dz такой, что его грань sn
совпадает с боковой поверхностью
балки.
Очевидно, что в сечениях ps и mn
возникают нормальные напряжения,
причем они будут отличаться на бесконечно малую величину.
Из чертежа видно, что для того, чтобы элемент pmns был уравновешен,
необходимо, чтобы в сечении pn
возникали напряжения, параллельные оси Z и направленные так, как
показано на рисунке.
Это будут касательные напряжения zx
.
34.
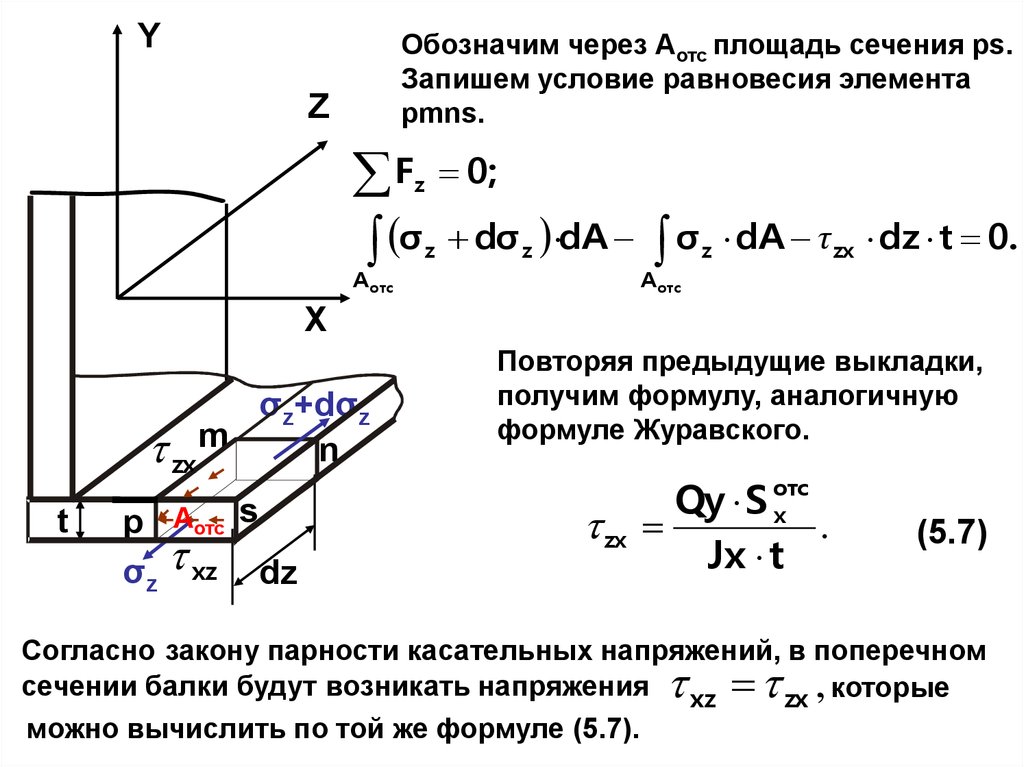
YОбозначим через Аотс площадь сечения ps.
Запишем условие равновесия элемента
pmns.
Z
F
σ
0;
z
z
dσ z dA
A отс
σ
z
dA τ zx dz t 0.
A отс
X
σz+dσz
n
zx m
t
p Аотс s
σz xz dz
Повторяя предыдущие выкладки,
получим формулу, аналогичную
формуле Журавского.
zx
Qy S отс
x
.
Jx t
(5.7)
Согласно закону парности касательных напряжений, в поперечном
сечении балки будут возникать напряжения xz zx , которые
можно вычислить по той же формуле (5.7).
35.
Yb-r
К CK
b
t
r
yCK
h
C
X
d
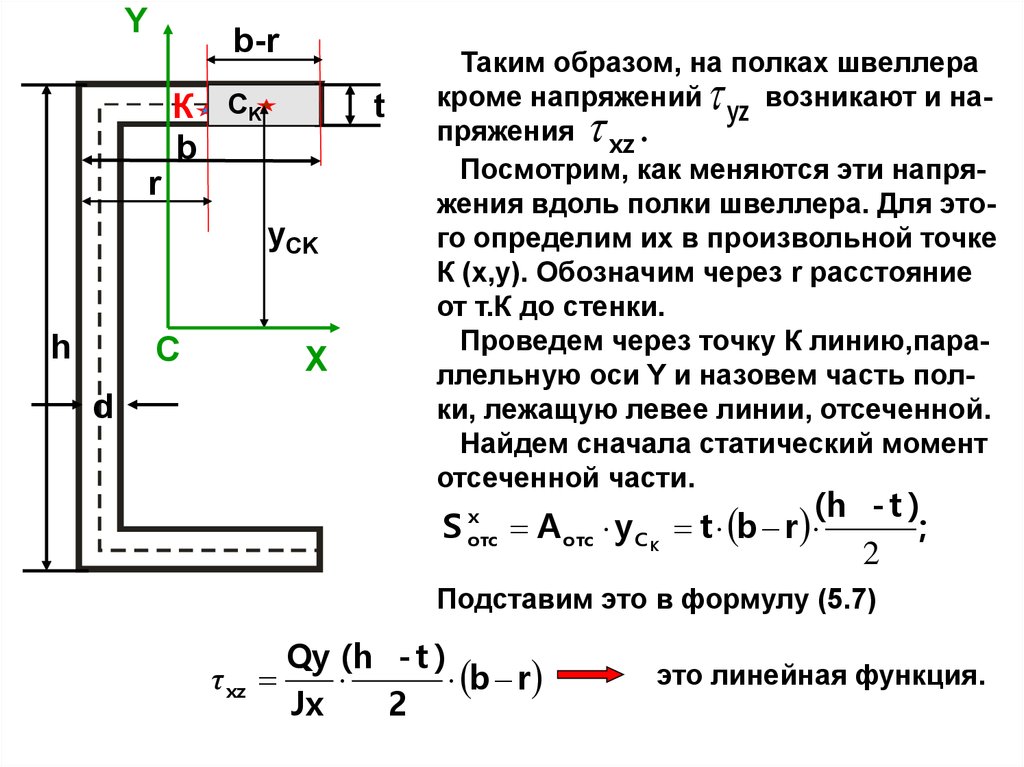
Таким образом, на полках швеллера
кроме напряжений yz возникают и напряжения xz
Посмотрим, как меняются эти напряжения вдоль полки швеллера. Для этого определим их в произвольной точке
К (x,y). Обозначим через r расстояние
от т.К до стенки.
Проведем через точку К линию,параллельную оси Y и назовем часть полки, лежащую левее линии, отсеченной.
Найдем сначала статический момент
отсеченной части.
.
S
x
отс
A отс y C K
(h - t )
t b r
;
2
Подставим это в формулу (5.7)
τ xz
Qy (h - t )
b r
Jx
2
это линейная функция.
36.
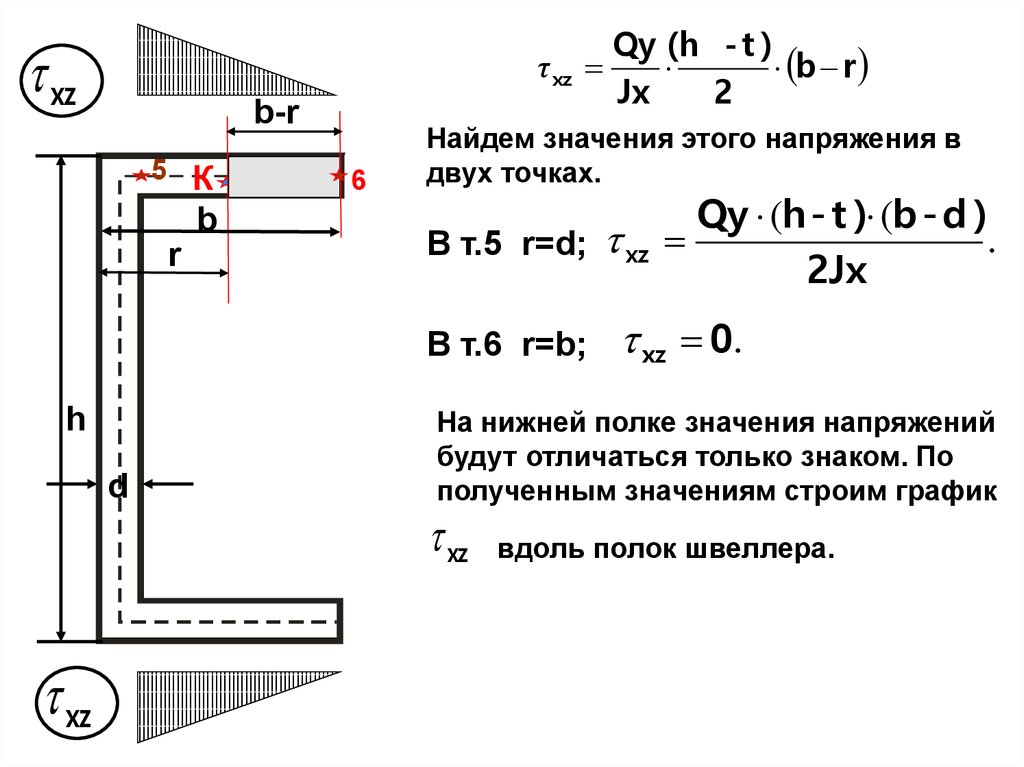
xzτ xz
b-r
5 К
b
r
6
Найдем значения этого напряжения в
двух точках.
В т.5 r=d;
В т.6 r=b;
h
d
xz
Qy (h - t )
b r
Jx
2
xz
Qy (h - t ) (b - d )
.
2Jx
xz 0.
На нижней полке значения напряжений
будут отличаться только знаком. По
полученным значениям строим график
xz
вдоль полок швеллера.
37.
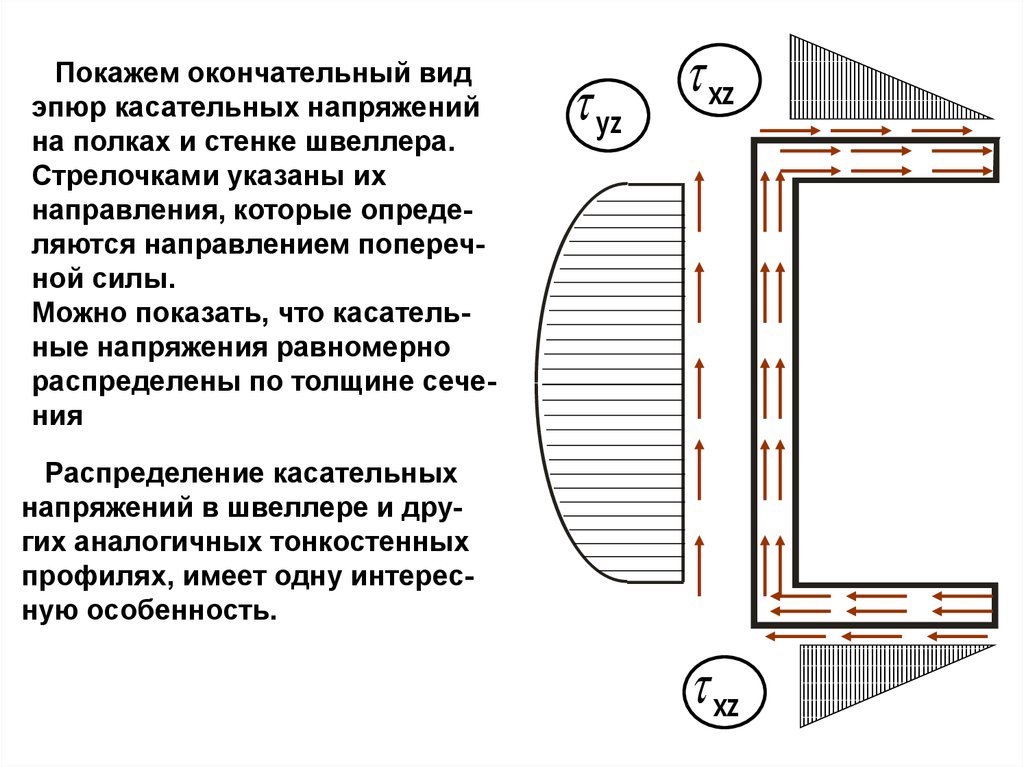
Покажем окончательный видэпюр касательных напряжений
на полках и стенке швеллера.
Стрелочками указаны их
направления, которые определяются направлением поперечной силы.
Можно показать, что касательные напряжения равномерно
распределены по толщине сечения
yz
xz
Распределение касательных
напряжений в швеллере и других аналогичных тонкостенных
профилях, имеет одну интересную особенность.
xz
38.
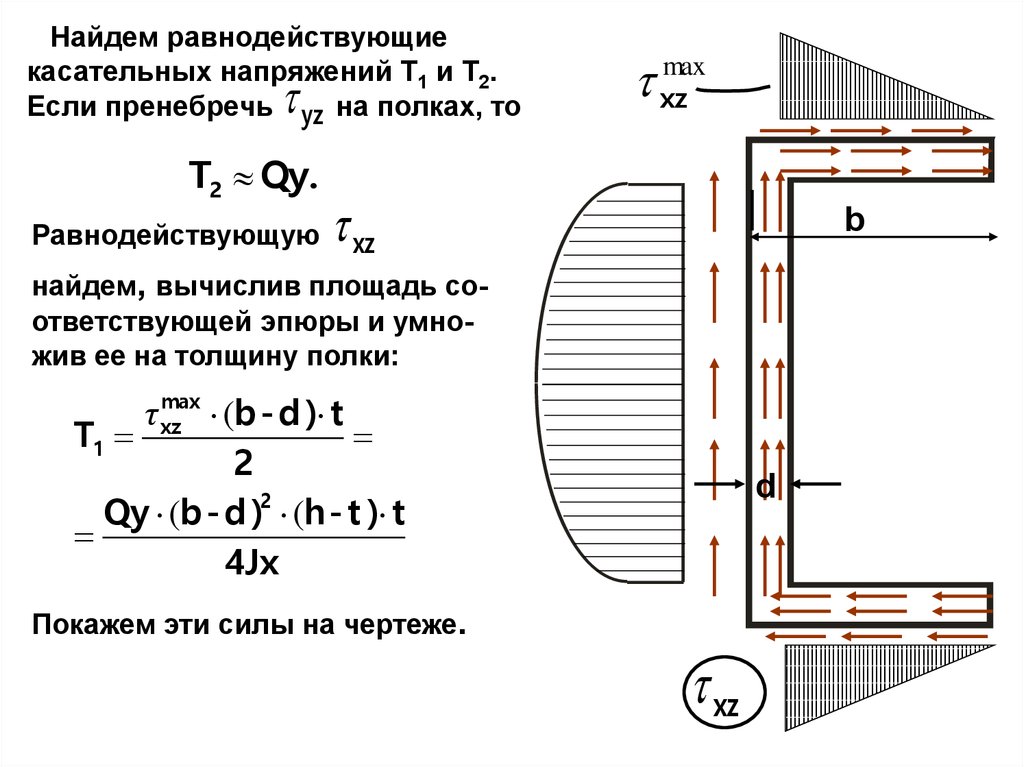
Найдем равнодействующиекасательных напряжений T1 и T2.
Если пренебречь yz на полках, то
T2 Qy.
Равнодействующую
max
xz
xz
b
найдем, вычислив площадь соответствующей эпюры и умножив ее на толщину полки:
max
τ xz
(b - d ) t
T1
2
Qy (b - d )2 (h - t ) t
4Jx
d
Покажем эти силы на чертеже.
xz
39.
T1T2
O
h/2
С
е
T1
Из рисунка видно, что силы Т1 и Т2 стремятся повернуть сечение вокруг центра
тяжести т.С в одну и ту же сторону, то есть
в сечении возникает дополнительное
внутреннее усилие – крутящий момент Мz.
За счет этого усилия в сечении возникают
и дополнительные напряжения, что неблагоприятно сказывается на прочности балки. Чтобы это предотвратить, необходимо
прикладывать внешнюю нагрузку так, чтобы она уравновешивалась внутренними
усилиями без появления кручения. Обозначим через О соответствующую точку.
Тогда
h
mom
0;
T
2 T2 е 0.
O
1
2
T1 h Qy (b - d )2 (h - t ) t(h
t ) (b - d )2 (h - t )2 t
е
T2
4Jx Qy
4Jx
Точка О называется центром изгиба.
40.
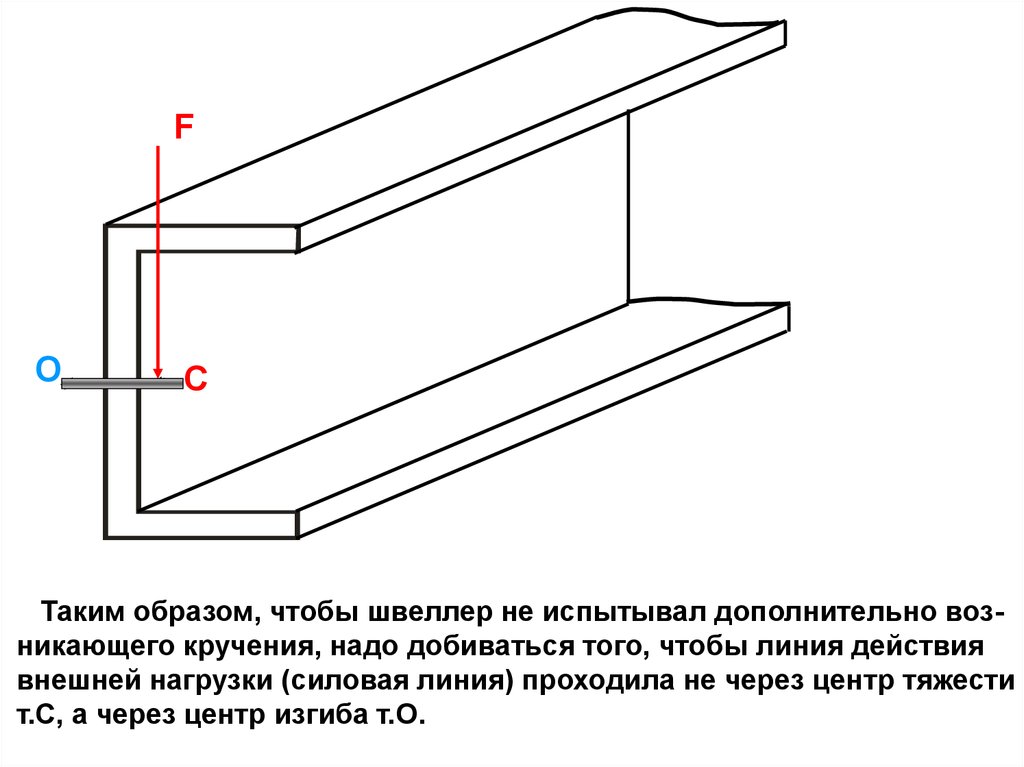
FO
С
Таким образом, чтобы швеллер не испытывал дополнительно возникающего кручения, надо добиваться того, чтобы линия действия
внешней нагрузки (силовая линия) проходила не через центр тяжести
т.С, а через центр изгиба т.О.
41.
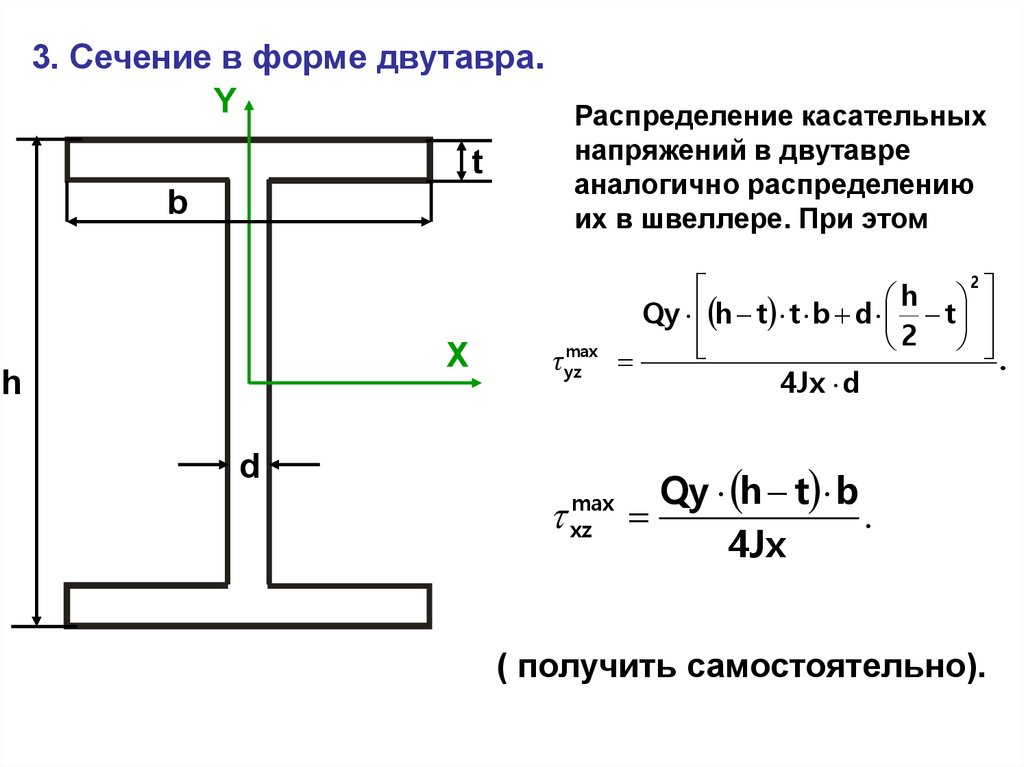
3. Сечение в форме двутавра.Y
Распределение касательных
напряжений в двутавре
t
аналогично распределению
b
их в швеллере. При этом
X
h
max
τ yz
d
max
xz
2
h
Qy h t t b d t
2
.
4Jx d
Qy h t b
.
4Jx
( получить самостоятельно).
42.
maxxz
xz
Y
X
yzmax
yz
xz
43.
Исследование напряженного состояния в точкебалки.
X
Y
F
Z
X
Z
нейтральный
слой
Рассмотрим консольную балку прямоугольного поперечного сечения, нагруженную, например, сосредоточенной силой.
Проведем в этой
балке произвольное
сечение и отбросим
часть балки, лежащую, например,
справа от сечения.
Выберем в этом
сечении произвольную точку.
44.
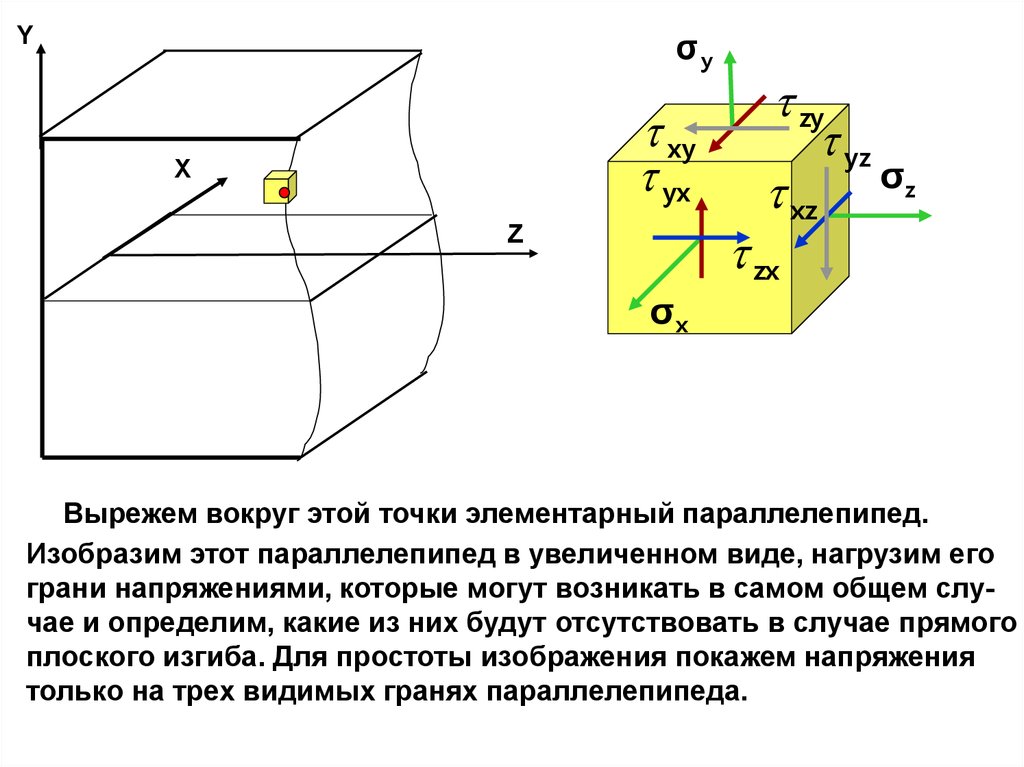
σyY
xy
yx
X
Z
σx
zy
yz
xz σ z
zx
Вырежем вокруг этой точки элементарный параллелепипед.
Изобразим этот параллелепипед в увеличенном виде, нагрузим его
грани напряжениями, которые могут возникать в самом общем случае и определим, какие из них будут отсутствовать в случае прямого
плоского изгиба. Для простоты изображения покажем напряжения
только на трех видимых гранях параллелепипеда.
45.
σyY
xy
yx
X
Z
σx
zy
yz
xz σ z
zx
1). Передняя грань параллелепипеда
совпадает с боковой поверхностью
балки, свободной от нагрузки, и поэтому напряжения на этой грани отсутствуют
σ x zx
yx 0;
2). В силу закона парности касательных напряжений
xz zx 0; xy yx 0;
3). Нормальные напряжения на верхней грани параллелепипеда
отсутствуют в силу гипотезы о ненадавливании продольных волокон друг на друга, то есть σ y 0.
46.
zyσz
σz
yz
σz
zy
yz
σz
Таким образом, у элементарного параллелепипеда имеется только одна пара свободных от напряжений площадок, то есть имеет
место плоское напряженное состояние.
Главные напряжения найдем по формуле (3.4):
2
σ 1,3
σz
σz
2
τ yz ,
2
2
главные направления по формуле (3.5):
(5.8)
tgα1,3
τ yz
σ 1,3
(5.9)
47.
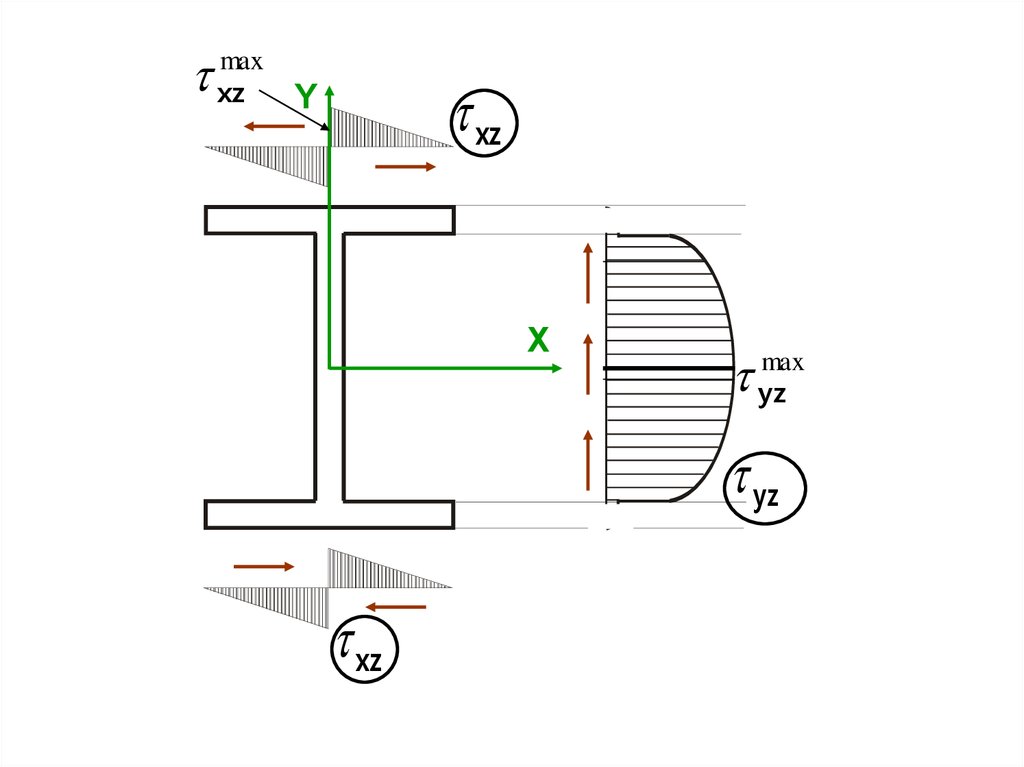
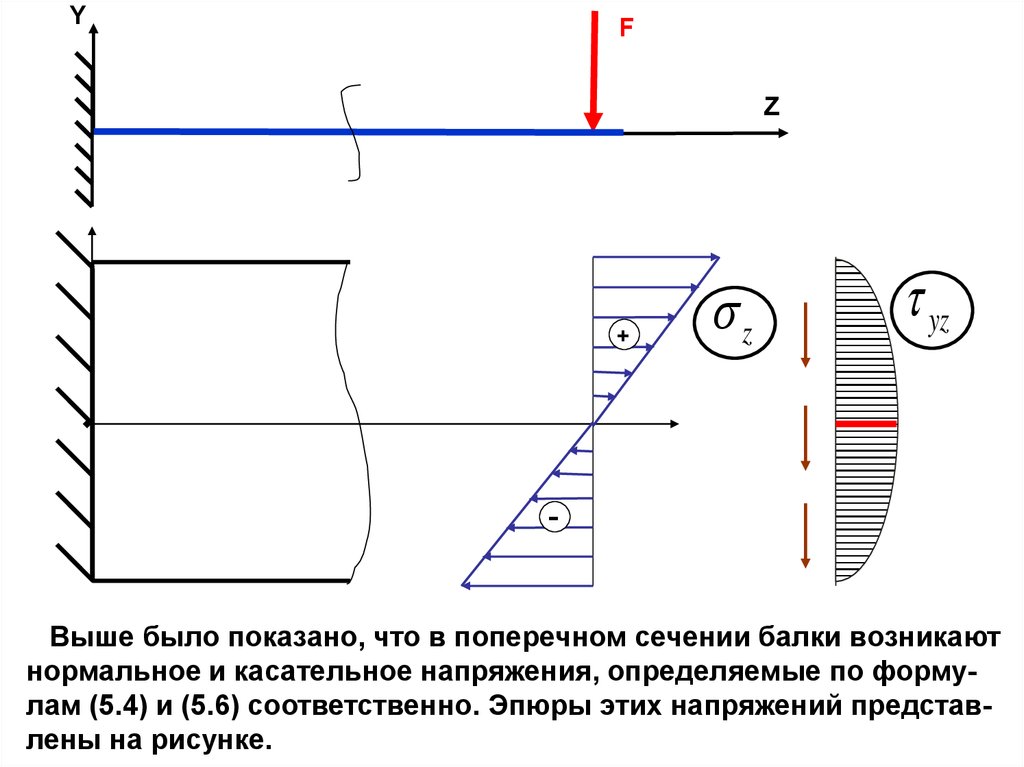
YF
Z
+
z
yz
-
Выше было показано, что в поперечном сечении балки возникают
нормальное и касательное напряжения, определяемые по формулам (5.4) и (5.6) соответственно. Эпюры этих напряжений представлены на рисунке.
48.
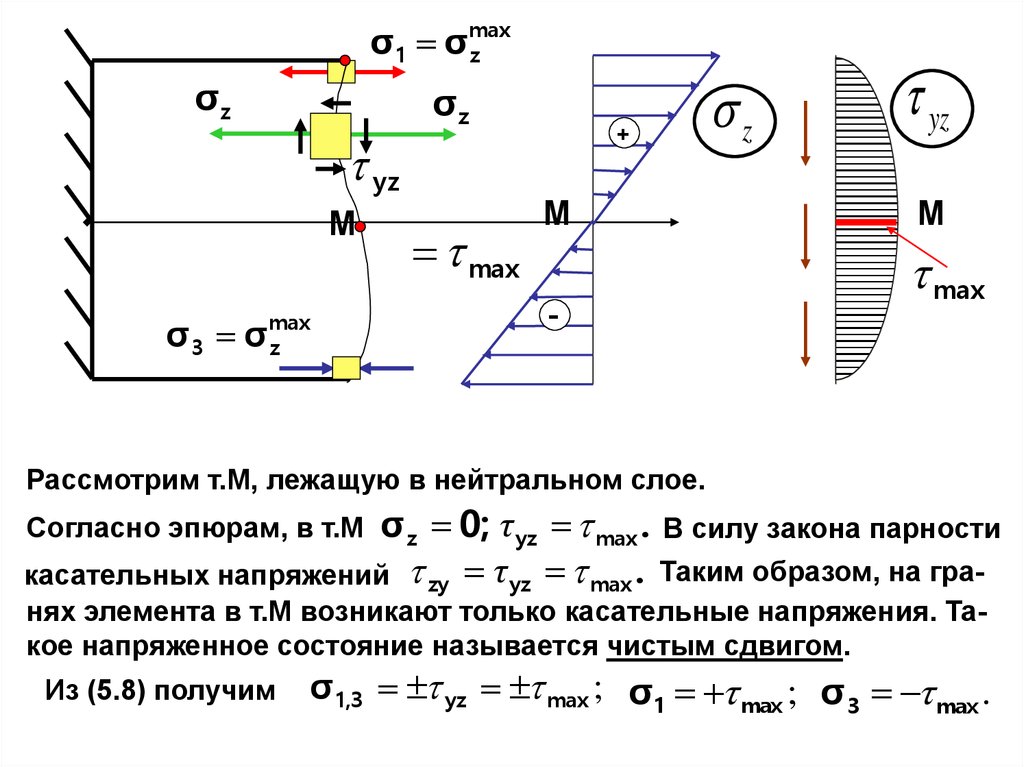
σ1 σ maxz
К1
σz
σ3 σ
yz
zy
max
z
К1
К1
σz
+
z
yz
-
К2
К2
К2
Рассмотрим т. К1 и т.К2, лежащие соответственно на верхнем и нижнем продольных волокнах балки.
Согласно эпюрам, в т.К1 σ z 0; τ yz 0. В силу закона парности касательных напряжений
zy τ yz 0.
ное состояние. Из (5.8) получим
Аналогично в т. К2
Имеем линейное напряжен-
σ 1 σ max
; σ 3 0.
z
σ 3 σ max
; σ 1 0.
z
49.
σ1 σ maxz
σz
σz
yz
М
σ 3 σ max
z
max
+
М
-
z
yz
М
max
Рассмотрим т.М, лежащую в нейтральном слое.
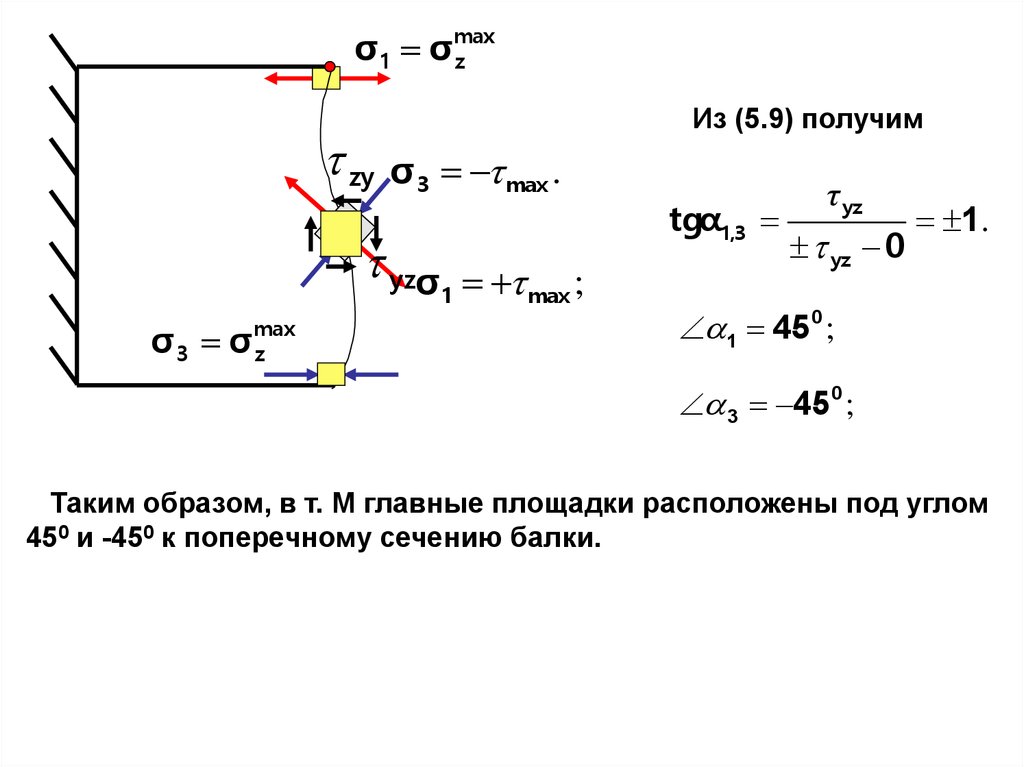
σ z 0; τ yz max . В силу закона парности
касательных напряжений zy τ yz max . Таким образом, на граСогласно эпюрам, в т.М
нях элемента в т.М возникают только касательные напряжения. Такое напряженное состояние называется чистым сдвигом.
Из (5.8) получим
σ 1,3 yz max ; σ1 max ; σ 3 max .
50.
σ1 σ maxz
zy
Из (5.9) получим
σ 3 max .
yzσ
σ3 σ
max
z
1
max ;
tgα1,3
τ yz
yz 0
1.
1 45 0 ;
3 45 0 ;
Таким образом, в т. М главные площадки расположены под углом
450 и -450 к поперечному сечению балки.
51.
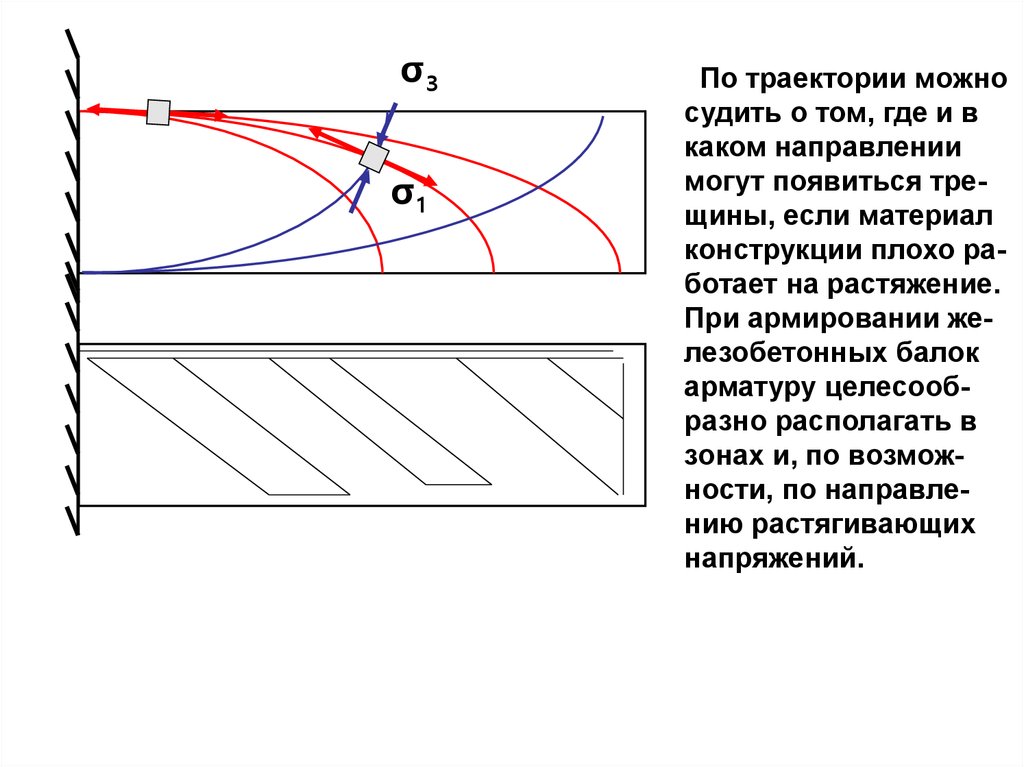
Траекторииσ3
σ min
σ1
Траектории
σ max
Определяя аналогичным образом направления главных напряжений в других точках
балки, мы можем изобразить так называемые главные траектории.
Так называются
линии, в каждой точке
которых касательная
совпадает с направлением главного напряжения (σ1 или σ3).
52.
σ3σ1
По траектории можно
судить о том, где и в
каком направлении
могут появиться трещины, если материал
конструкции плохо работает на растяжение.
При армировании железобетонных балок
арматуру целесообразно располагать в
зонах и, по возможности, по направлению растягивающих
напряжений.
53.
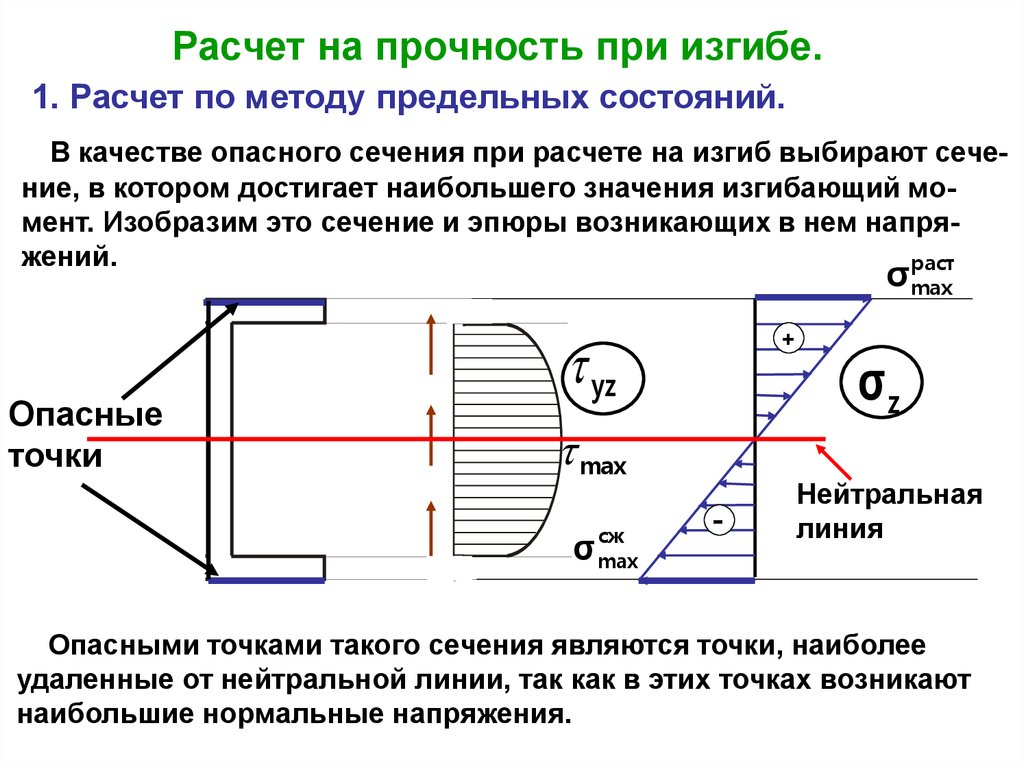
Расчет на прочность при изгибе.1. Расчет по методу предельных состояний.
В качестве опасного сечения при расчете на изгиб выбирают сечение, в котором достигает наибольшего значения изгибающий момент. Изобразим это сечение и эпюры возникающих в нем напряжений.
раст
σ max
Опасные
точки
yz
+
max
σ
сж
max
-
σz
Нейтральная
линия
Опасными точками такого сечения являются точки, наиболее
удаленные от нейтральной линии, так как в этих точках возникают
наибольшие нормальные напряжения.
54.
σ растmax
yz
Опасные
точки
+
max
σ
сж
max
-
σz
Нейтральная
линия
В этих точках, как было показано выше, возникает линейное напряженное состояние, поэтому по любой теории прочности условие
прочности записывается в виде:
σ max
R.
z
Если балка выполнена из хрупкого материала, то записываются
два условия прочности:
σ раст
max R раст
сж
σ max
R сж
55.
В опасных точках сечения балки возникает линейное напряженноесостояние; во всех остальных – плоское. В частности, в точках, лежащих на нейтральной линии
σ1 max ;
σ 3 max .
Тогда, используя, например, четвертую теорию прочности, получим
σ
IV
экв
1
σ1 2 σ 3 2 σ 3 σ1 2
2
1
2
2
2 3
max R
max max 2 max
2
Отсюда
max R ср ,
где Rср– это расчетное сопротивление на срез;
R cр
R
0,58R
3
56.
Отметим, что точно также будет записываться условие прочностиво всех случаях состояния чистого сдвига.
Условие прочности в точках, лежащих на нейтральной линии (условие прочности по касательным напряжениям), проверяют, если
поперечная сила достигает наибольшего значения в опасном сечении балки.
Кроме того, условие прочности по касательным напряжениям важно проверять в следующих случаях:
1) если балка короткая;
2) если она нагружена большими сосредоточенными силами,
приложенными на малых расстояниях от опор. В таких балках поперечные силы могут иметь значительную величину,
в то время, как изгибающие моменты оказываются сравнительно небольшими;
3) если балка деревянная. Для деревянных балок расчет на
прочность по касательным напряжениям может иметь решающее значение, так как дерево плохо сопротивляется скалыванию вдоль волокон.
57.
σ растmax
yz
+
max
-
σz
Нейтральная
линия
сж
σ max
В тонкостенных стержнях могут быть точки, в которых и нормальные, и касательные напряжения одновременно достигают больших
значений (например, точки стенки швеллера, лежащие на линии сопряжения полки и стенки).
В этом случае при расчете на прочность также используются теории прочности (3.8).
58.
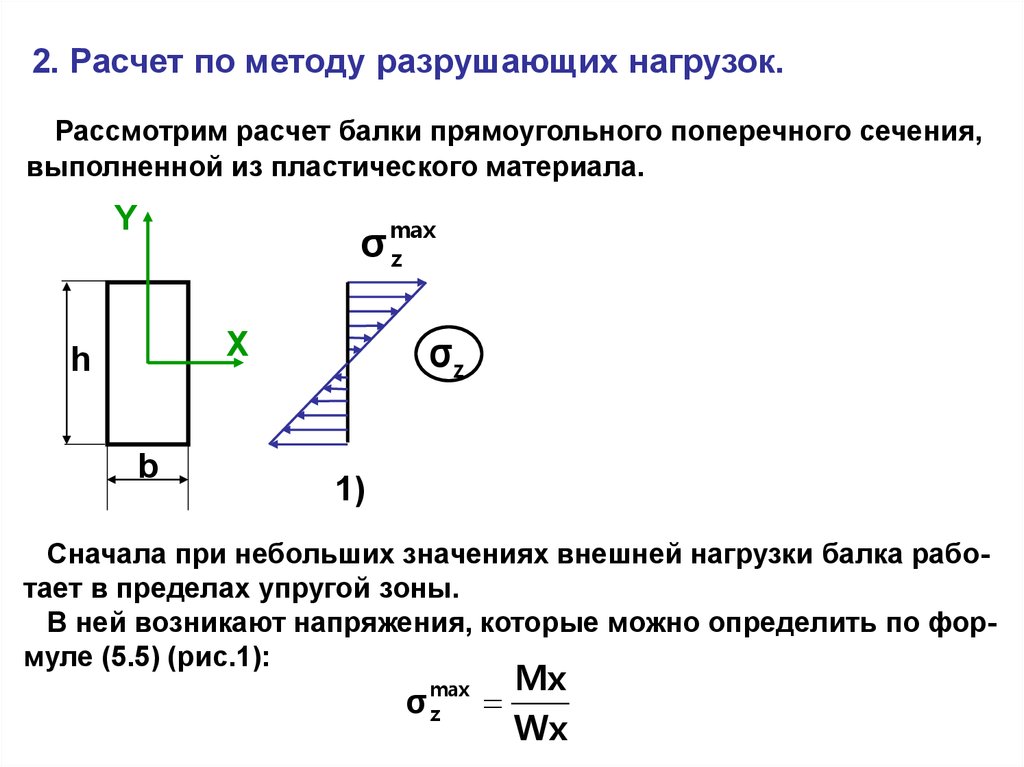
2. Расчет по методу разрушающих нагрузок.Рассмотрим расчет балки прямоугольного поперечного сечения,
выполненной из пластического материала.
Y
σ max
z
σz
X
h
b
1)
Сначала при небольших значениях внешней нагрузки балка работает в пределах упругой зоны.
В ней возникают напряжения, которые можно определить по формуле (5.5) (рис.1):
σ
max
z
Mx
Wx
59.
σzY
σ
max
z
σт
σ max
σт
z
σт
X
h
b
1)
2)
3)
4)
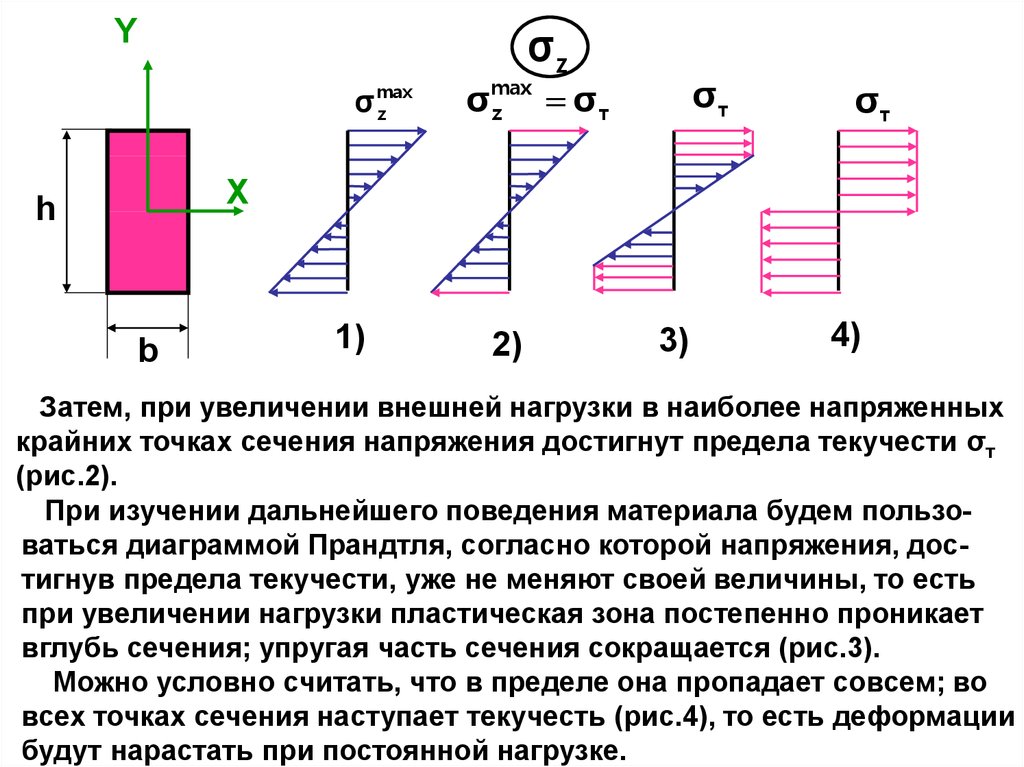
Затем, при увеличении внешней нагрузки в наиболее напряженных
крайних точках сечения напряжения достигнут предела текучести σт
(рис.2).
При изучении дальнейшего поведения материала будем пользоваться диаграммой Прандтля, согласно которой напряжения, достигнув предела текучести, уже не меняют своей величины, то есть
при увеличении нагрузки пластическая зона постепенно проникает
вглубь сечения; упругая часть сечения сокращается (рис.3).
Можно условно считать, что в пределе она пропадает совсем; во
всех точках сечения наступает текучесть (рис.4), то есть деформации
будут нарастать при постоянной нагрузке.
60.
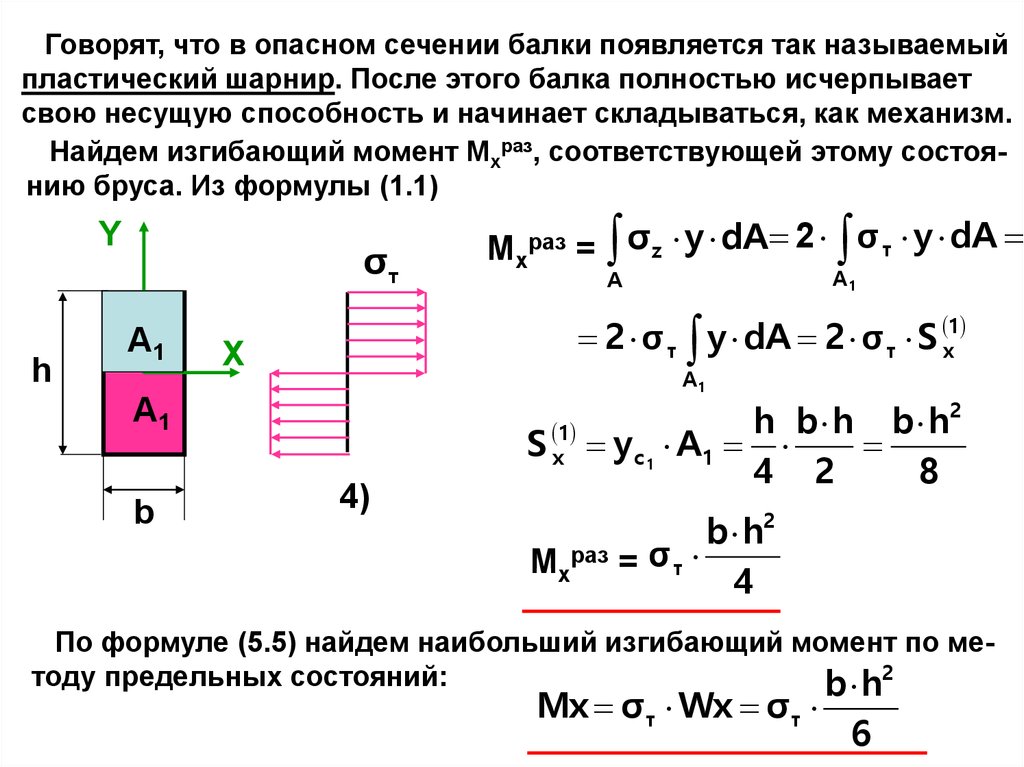
Говорят, что в опасном сечении балки появляется так называемыйпластический шарнир. После этого балка полностью исчерпывает
свою несущую способность и начинает складываться, как механизм.
Найдем изгибающий момент Мxраз, соответствующей этому состоянию бруса. Из формулы (1.1)
Y
h
σт
А1
A1
A
2 σ т y dA 2 σ т S x1
X
A1
А1
b
Mxраз = σ z y dA 2 σ т y dA
4)
2
h
b
h
b
h
S x1 y c 1 A1
4 2
8
b h2
Mxраз = σ т
4
По формуле (5.5) найдем наибольший изгибающий момент по методу предельных состояний:
b h2
Мx σ т Wx σ т
6
61.
Сравним полученные по двум разным методам значения моментов:bh2
σт
Mраз
x
4 1,5.
bh2
Mx
σт
6
Для круга это отношение равно 1,7; для двутавра – 1,15.
Таким образом, мы показали, что метод разрушающих нагрузок
и при изгибе, как и при осевом растяжении-сжатии, позволяет
вскрывать дополнительные резервы конструкции.
62.
Подбор рационального сечения балки.1. Пластический материал.
Подбор сечения балки осуществляется с помощью условия
прочности:
σ
max
z
R
Mx
R
Wx
Wx
Mx
R
При подборе сечения следует стремиться к тому, чтобы подобранное сечение было возможно более рациональным, то есть
таким, для которого отношение
Wx
β
A
было возможно большим. Это означает, что при минимальной площади, то есть при минимальных затратах материала, надо стремиться получить как можно больший момент сопротивления, то есть получить наибольшую прочность балки.
63.
Так как по определениюJx
Wx
,
ymax
то Wx будет тем больше, чем больше Jx. По определению
Jx у dA,
2
A
то есть Jx, в свою очередь, будет тем больше, чем дальше располагаются от нейтральной линии частицы площади сечения.
Поясним это на следующем примере. Рассмотрим два сечения,
составленных из одних и тех же элементов: два тавровых и восемь
прямоугольных.
5а
а
2а
2а
а
а
64.
5аПервое сечение – прямоугольное.
Найдем величину β для этого сечения.
6а
A b h 5a 6a 30a ;
2
b h2 5a 6a
Wx
30a 3 ;
6
6
2
Wx
β
a.
A
65.
y13а
2,5а
2а
а
C
x2
x1
x
Второе сечение – типа двутаврового.
Найдем сначала момент инерции этого сечения относительно оси X:
J X 2 (J X1 J X2 ) 2 (J X1 a 2 A1 J X 2 2,5a A 2 )
2
3
a 2a
13a
a
2
2
2 (
a a 2a
2,5a 13a a) 170a 4
12
12
3
Момент сопротивления будет равен
Jx
170a 4
Wx
57a 3
ymax
3a
66.
Площадь этого сечения такая же, как и прямоугольного, посколькуоно составлено из тех же элементов, А=30а2. Тогда
Wx 57а 3
β
1.9a.
2
A
30а
Таким образом, мы получили, что значение β для двутаврого сечения значительно больше, чем для прямоугольного, то есть двутавровое сечение более рационально, чем прямоугольное.
Этот же вывод можно получить и из других соображений. Изобразим прямоугольное сечение и покажем рядом с ним эпюру нормальных напряжений.
67.
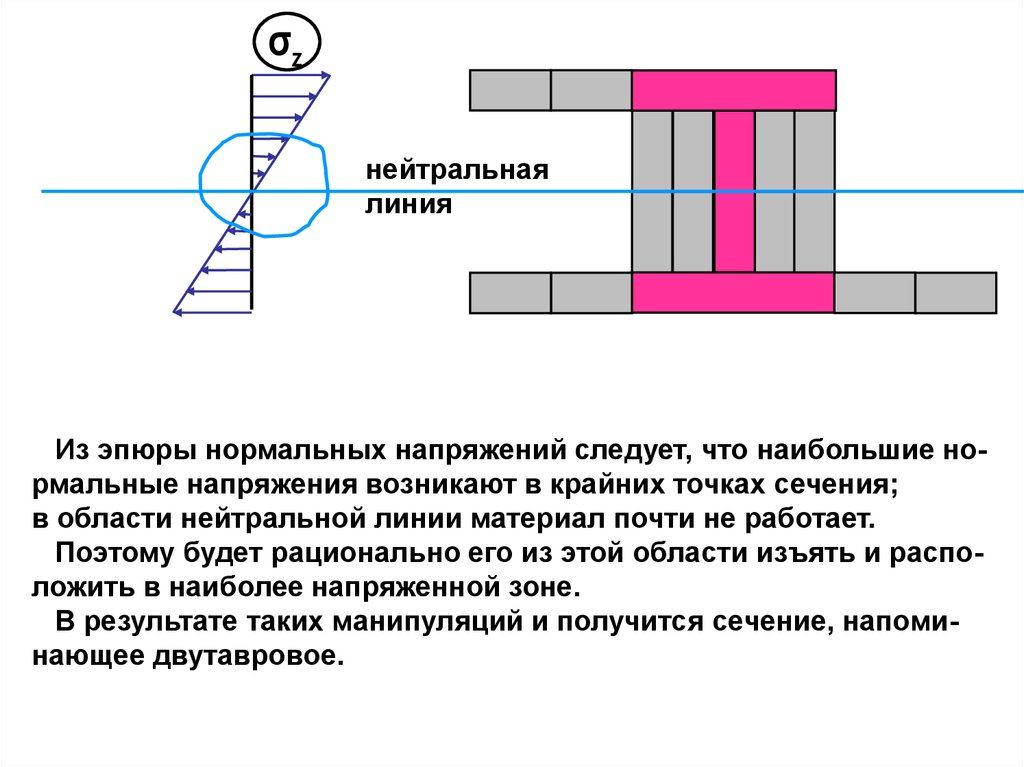
σzнейтральная
линия
Из эпюры нормальных напряжений следует, что наибольшие нормальные напряжения возникают в крайних точках сечения;
в области нейтральной линии материал почти не работает.
Поэтому будет рационально его из этой области изъять и расположить в наиболее напряженной зоне.
В результате таких манипуляций и получится сечение, напоминающее двутавровое.
68.
2. Хрупкий материал.Такие материалы хорошо работают на сжатие и значительно хуже—
на растяжение. Поэтому целесообразно, чтобы наибольшие растягивающие напряжения в таких балках были как можно меньше. Этого можно добиться в балках с поперечными сечениями, несимметричными относительно нейтральной линии. Рассмотрим опять
два сечения, составленных из одинаковых элементов : прямоугольное и тавровое. Предположим, что в балке растягиваются нижние
волокна.
В силу симметрии прямоугольного сечения наибольшие растягивающие и сжимающие напряжения в этом сечении будут одинаковы.
Попробуем сконструировать
новое сечение, перенося
материал из менее опасной
зоны сжатия в более опасную
зону растяжения.
σz
+
69.
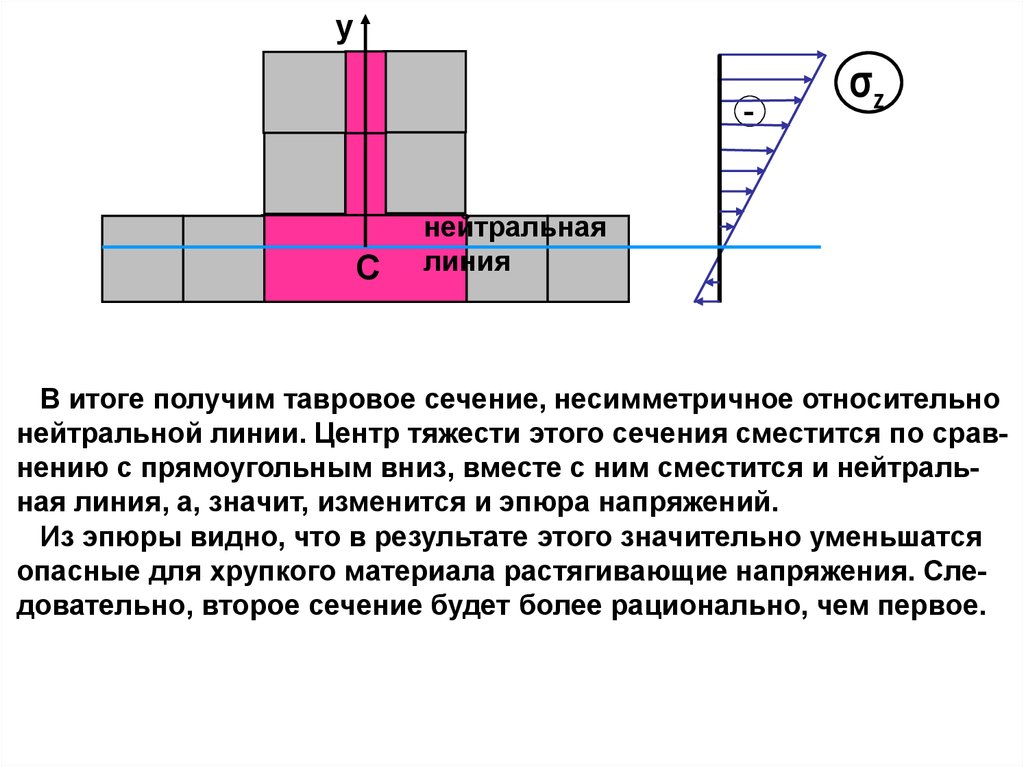
y-
C
σz
нейтральная
линия
В итоге получим тавровое сечение, несимметричное относительно
нейтральной линии. Центр тяжести этого сечения сместится по сравнению с прямоугольным вниз, вместе с ним сместится и нейтральная линия, а, значит, изменится и эпюра напряжений.
Из эпюры видно, что в результате этого значительно уменьшатся
опасные для хрупкого материала растягивающие напряжения. Следовательно, второе сечение будет более рационально, чем первое.
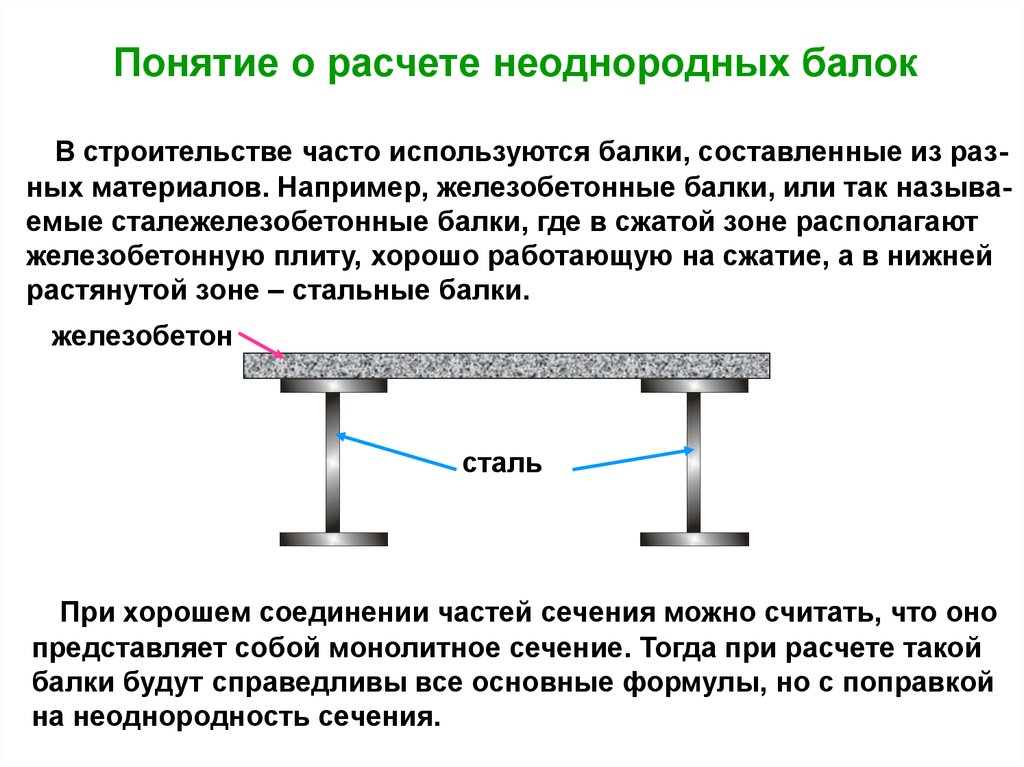
70.
Понятие о расчете неоднородных балокВ строительстве часто используются балки, составленные из разных материалов. Например, железобетонные балки, или так называемые сталежелезобетонные балки, где в сжатой зоне располагают
железобетонную плиту, хорошо работающую на сжатие, а в нижней
растянутой зоне – стальные балки.
железобетон
сталь
При хорошем соединении частей сечения можно считать, что оно
представляет собой монолитное сечение. Тогда при расчете такой
балки будут справедливы все основные формулы, но с поправкой
на неоднородность сечения.
71.
Эту поправку внесем аналогично тому, как это было сделано приосевом растяжении-сжатии:
1) во всех основных формулах изгиба заменим обычные геометрические характеристики на приведенные:
Aпр ni Ai; Jx пр ni Jx i;
i
где
Ei
ni
E1
i
Sx пр ni Sx i,
i
-- коэффициент приведения i-го материала к основному (первому) материалу;
2) введем этот коэффициент во все основные формулы изгиба:
Mx
σ i ni
y;
Jx пр
y i ni
Qy S отс
x пр
Jx пр b
,
и т.д.
72.
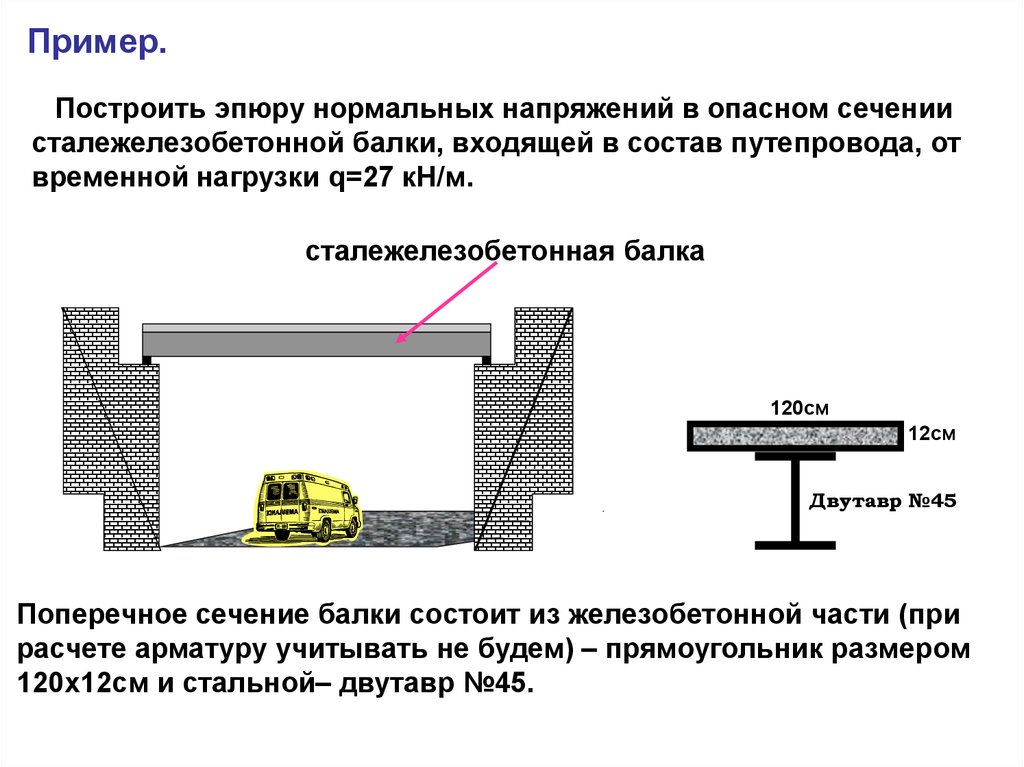
Пример.Построить эпюру нормальных напряжений в опасном сечении
сталежелезобетонной балки, входящей в состав путепровода, от
временной нагрузки q=27 кН/м.
сталежелезобетонная балка
120см
12см
Двутавр №45
Поперечное сечение балки состоит из железобетонной части (при
расчете арматуру учитывать не будем) – прямоугольник размером
120х12см и стальной– двутавр №45.
73.
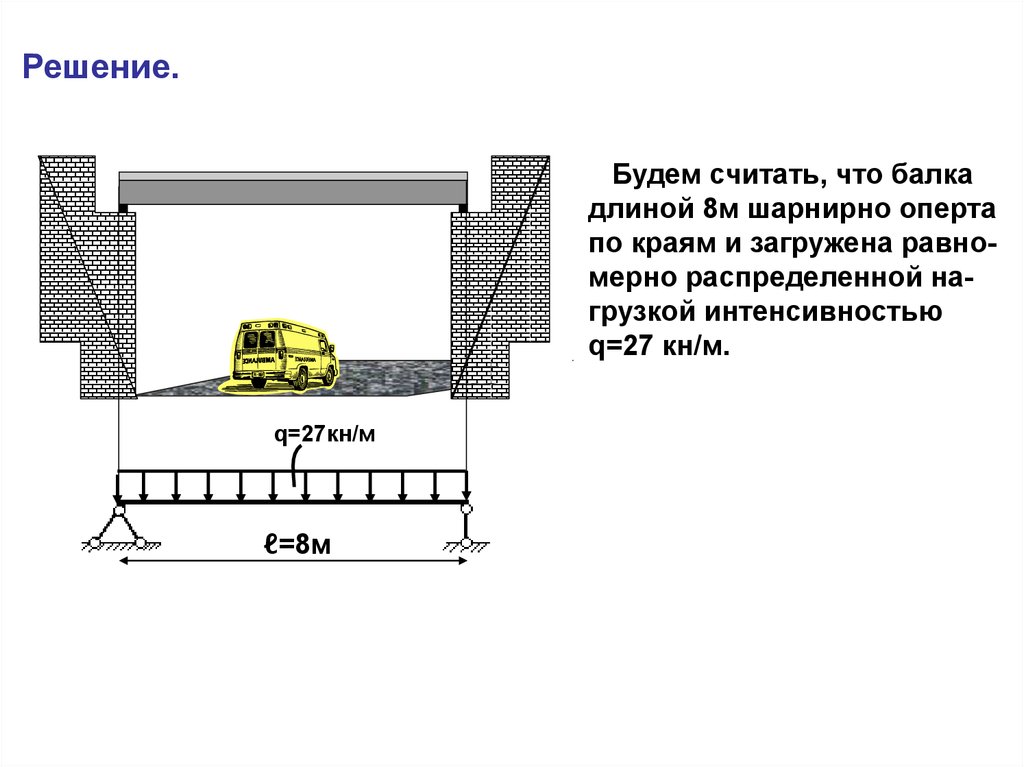
Решение.Будем считать, что балка
длиной 8м шарнирно оперта
по краям и загружена равномерно распределенной нагрузкой интенсивностью
q=27 кн/м.
q=27кн/м
ℓ=8м
74.
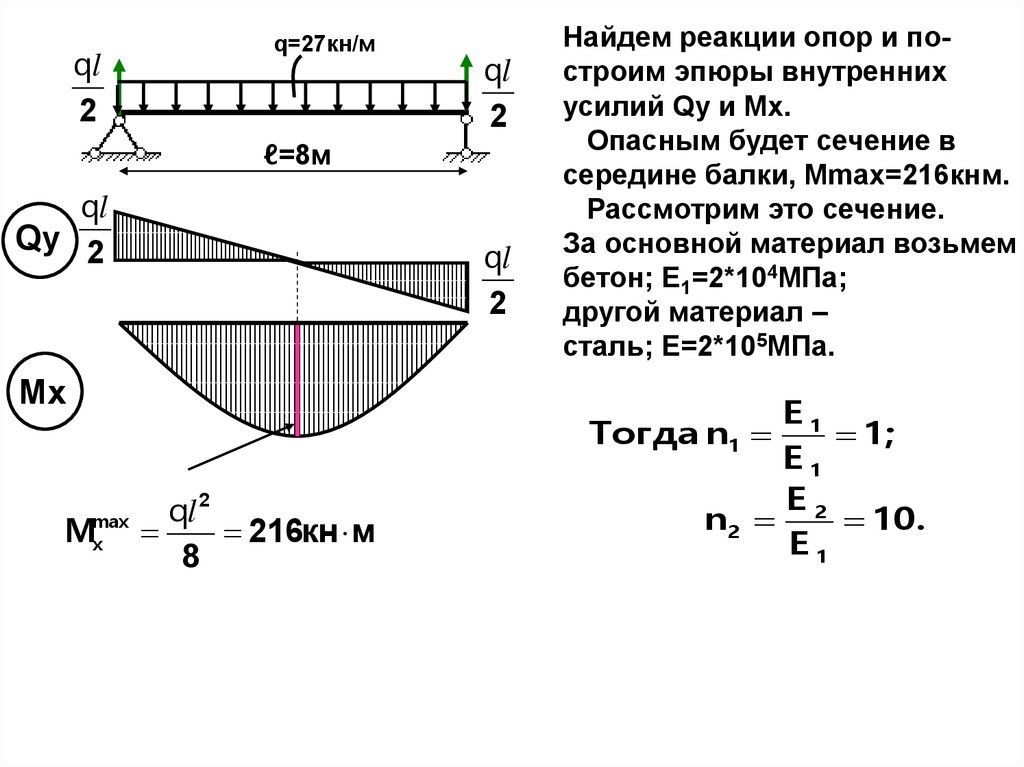
ql2
q=27кн/м
ql
2
ℓ=8м
ql
Qy 2
ql
2
Мx
M
max
x
ql 2
216кн м
8
Найдем реакции опор и построим эпюры внутренних
усилий Qy и Mx.
Опасным будет сечение в
середине балки, Мmax=216кнм.
Рассмотрим это сечение.
За основной материал возьмем
бетон; Е1=2*104МПа;
другой материал –
сталь; Е=2*105МПа.
E1
Тогда n1
1;
E1
E2
n2
10.
E1
75.
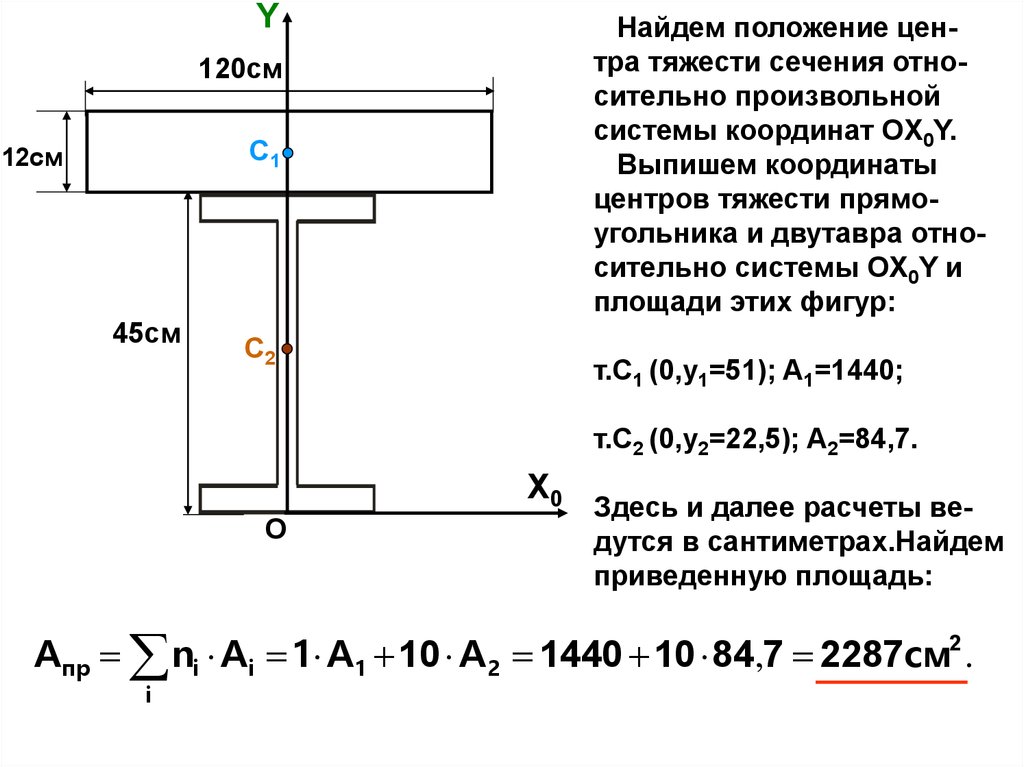
YНайдем положение центра тяжести сечения относительно произвольной
системы координат OX0Y.
Выпишем координаты
центров тяжести прямоугольника и двутавра относительно системы OX0Y и
площади этих фигур:
120см
C1
12см
45см
C2
т.С1 (0,y1=51); A1=1440;
т.С2 (0,y2=22,5); A2=84,7.
X0
O
Здесь и далее расчеты ведутся в сантиметрах.Найдем
приведенную площадь:
Aпр ni Ai 1 A1 10 A 2 1440 10 84,7 2287см2 .
i
76.
YКоординату центра тяжести найдем по формуле:
120см
C1
12см
yc
X
45см
C2
O
yc=40,5см
C
Sx пр
А пр
y1 A1пр y 2 A 2пр
А пр
y1 n1A1 y 2 n2 A 2
Апр
X0
51 1 1440 22,5 10 84,7
2287
40,5см
Покажем точку С -- центр тяжести – на чертеже.
Так как ось Y совпадает с осью симметрии фигуры, то проведенные
через точку С оси X и Y будут главными центральными осями
сечения.
77.
YНайдем приведенный
момент инерции:
120см
C1
12см
X1
а1
i
X
C
а2
45см
Jx пр ni Jx i
C2
X2
40,5см
(n1J X1 n2J X2 )
(J X1 10J X2 )
2
1
(J X1 a A1 )
2
10(J X 2 a 2 A 2 )
120 123
(
(51 40,5)2 1440) 10(27696 (40,5 22,5)2 84,7)
12
726000см4 0,00726м4
78.
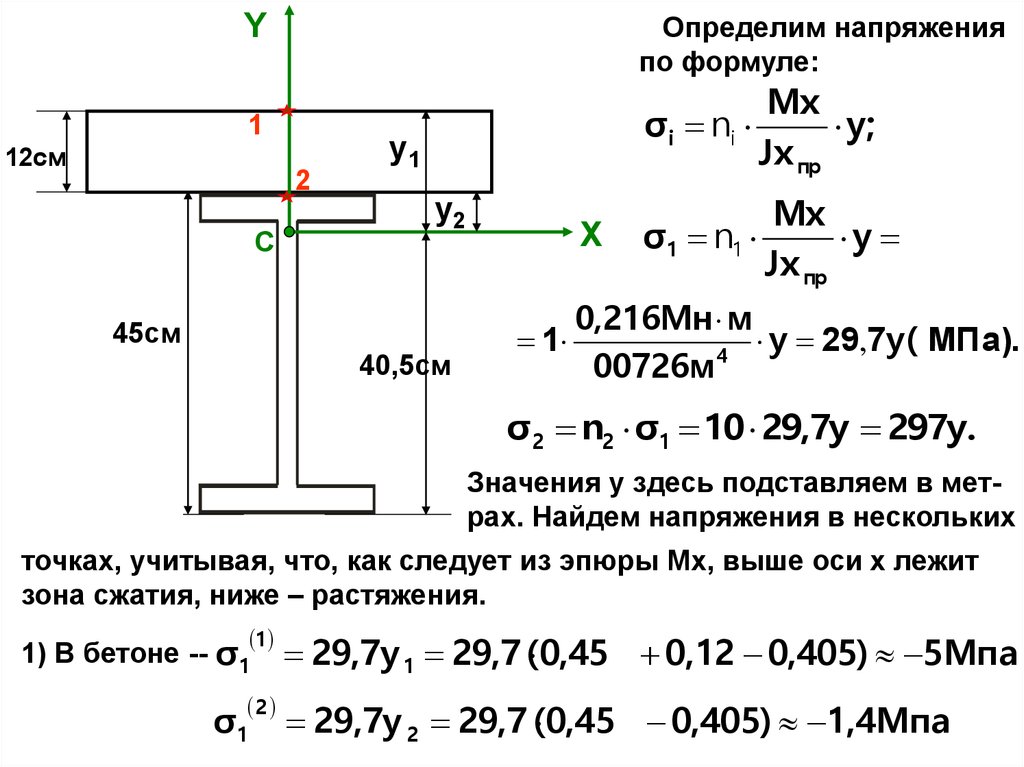
Определим напряженияпо формуле:
Y
1
12см
2
C
Mx
σ i ni
y;
Jx пр
y1
y2
45см
40,5см
X
1
Mx
σ1 n1
y
Jx пр
0,216Мн м
y 29,7y( МПа).
4
00726м
σ 2 n2 σ1 10 29,7y 297y.
Значения y здесь подставляем в метрах. Найдем напряжения в нескольких
точках, учитывая, что, как следует из эпюры Mx, выше оси x лежит
зона сжатия, ниже – растяжения.
1
29,7y 1 29,7 (0,45
0,12 0,405) 5Мпа
2
29,7y 2 29,7 (0,45
0,405) 1,4Мпа
1) В бетоне -- σ 1
σ1
79.
σ z ,МПаY
5
1
1,4
2
y2
C
14
-
45см
y3=40,5см
+
3
2) В стали --
σ2
2
σ2
3
297y 2 297 (0,45
0,405) 14Мпа
120
297y 3 297 0,405 120Мпа
По найденным значениям строим эпюру напряжений.
Из эпюры видно, что вся бетонная часть балки лежит в сжатой зоне,
а в месте сопряжения двух разных материалов на эпюре возникает
скачок.

































 Механика
Механика








