Похожие презентации:
Формулы для радиусов вписанной и описанной окружностей треугольника (9 класс)
1.
Формулы для радиусов вписанной иописанной окружностей
треугольника.
Геометрия 9 класс.
2.
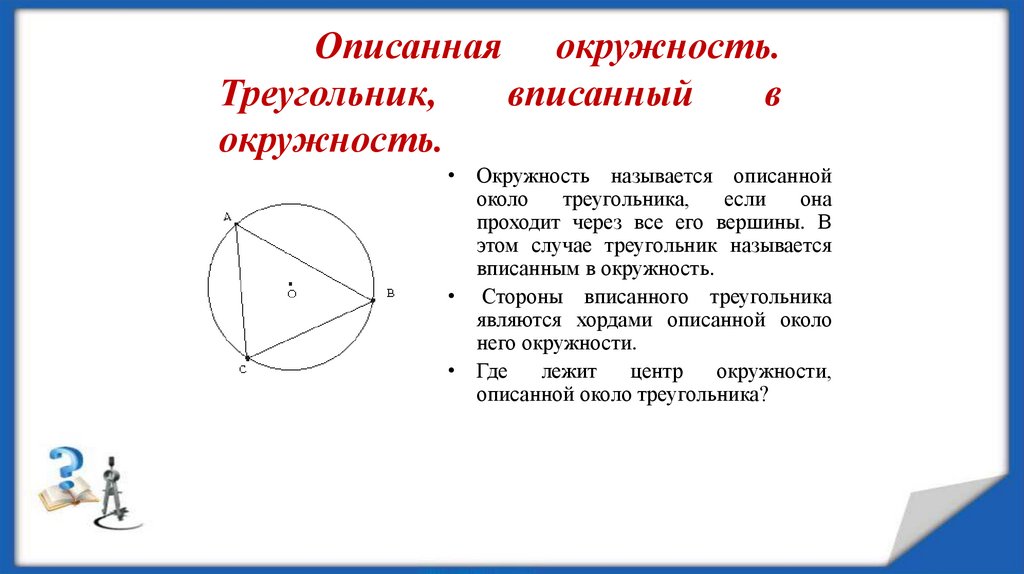
Описанная окружность.Треугольник,
вписанный
в
окружность.
• Окружность называется описанной
около
треугольника,
если
она
проходит через все его вершины. В
этом случае треугольник называется
вписанным в окружность.
• Стороны вписанного треугольника
являются хордами описанной около
него окружности.
• Где
лежит
центр
окружности,
описанной около треугольника?
3.
ВА
А
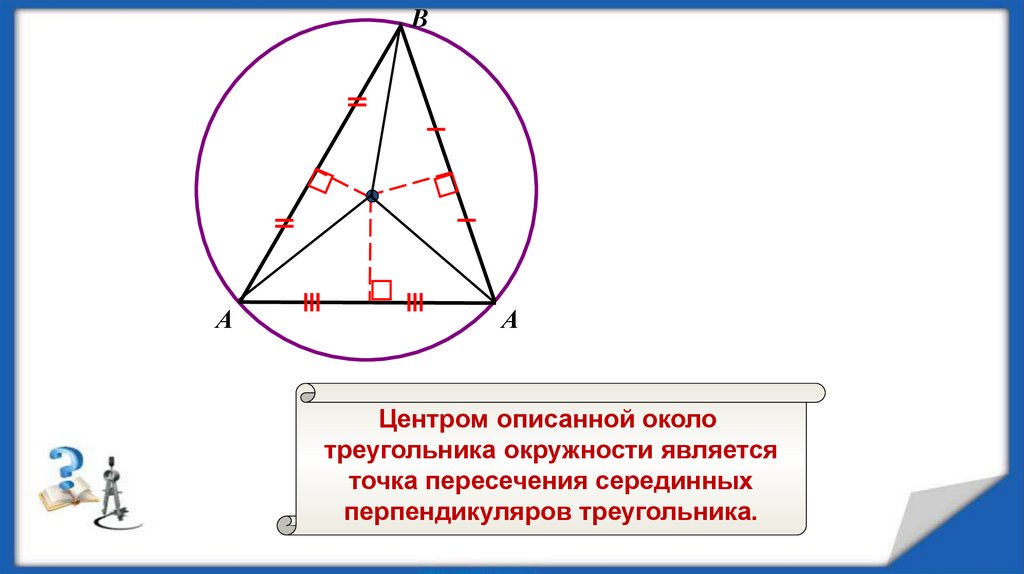
Центром описанной около
треугольника окружности является
точка пересечения серединных
перпендикуляров треугольника.
4.
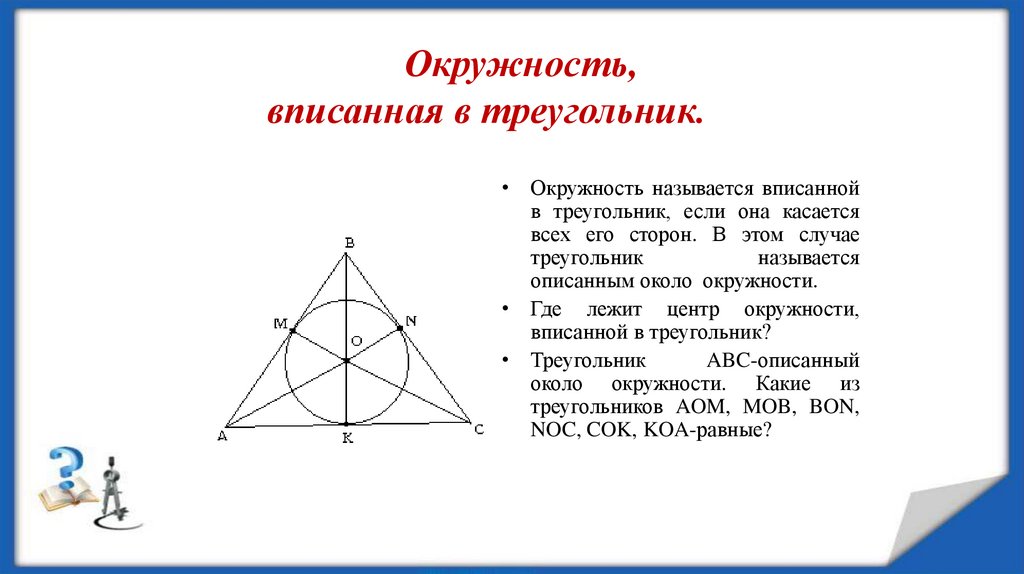
Окружность,вписанная в треугольник.
• Окружность называется вписанной
в треугольник, если она касается
всех его сторон. В этом случае
треугольник
называется
описанным около окружности.
• Где лежит центр окружности,
вписанной в треугольник?
• Треугольник
ABC-описанный
около окружности. Какие из
треугольников AOM, MOB, BON,
NOC, COK, KOA-равные?
5.
ВК
С
М
О
Р
А
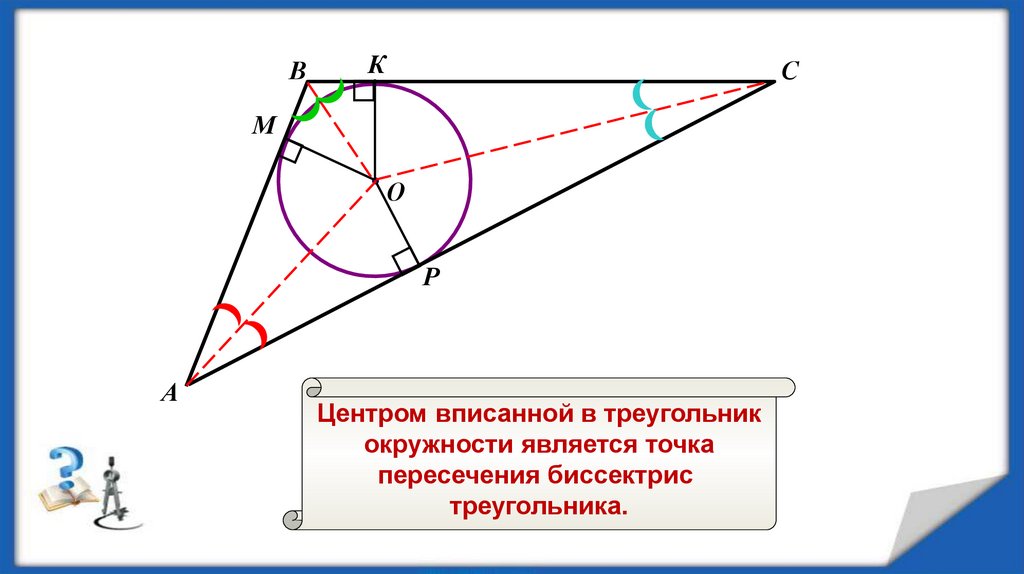
Центром вписанной в треугольник
окружности является точка
пересечения биссектрис
треугольника.
6.
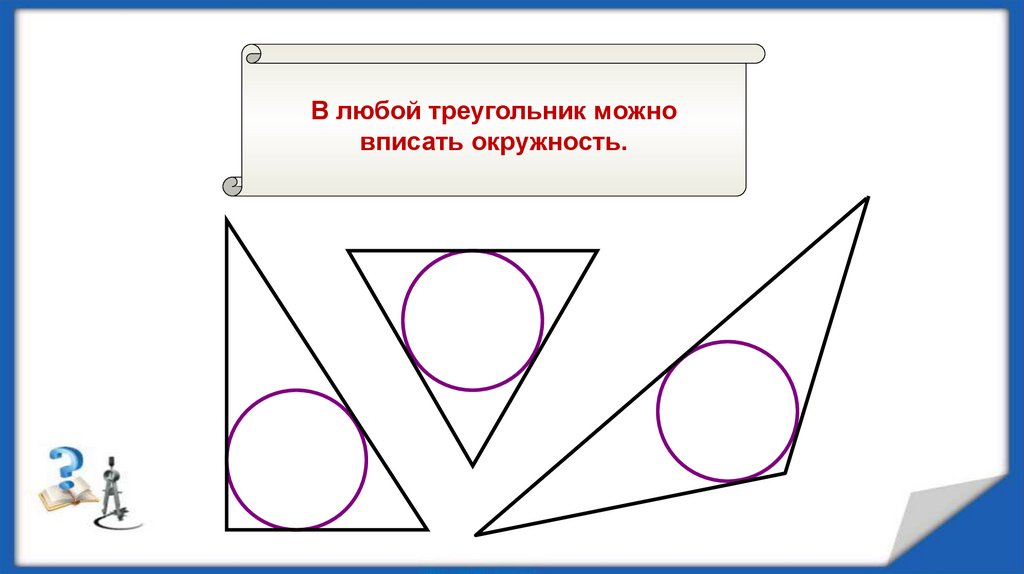
В любой треугольник можновписать окружность.
7.
8.
ЗаданиеВыведите следующие формулы для
радиусов описанной (R) и вписанной (r)
окружностей треугольника а: R a4Sbc , r a 2Sb c .
Дано:
АВС,
R –радиус описанной окружности,
r – радиус вписанной окружности,
а, в, с – стороны треугольника
Вывести: R abc , r 2S .
4S
a b c
9.
Решение:1)
à
b
c
a
2R R
sinα sinβ sinj
2sin α
Умножим на bc
abc
1
R
, т. к. S bcsin α, то 4S 2bcsin .
2bcsinα
2
abc
Следовательно, R
.
4S
10.
2)SABC = SAOB + SAOC + SBOC.
SABC =
1
1
1
1
с r b r a r r a b c
2
2
2
2
2S
r
и т. д.
a b c
11.
Формула для радиуса описанной около треугольникаокружности
a b c
R=
4S
c
a
R
b
Задача: найти радиус окружности, описанной около
равностороннего треугольника, сторона которого равна 4 см.
Решение:
a b c
, R=
R=
4S
a3
4S
43
4
4 3
(см)
R
3
4 4 3
3
a 2 3 42 3
S
4 3
4
4
Ответ:
4 3
см
3
12.
Домашнее задание:1.Выучить формулы радиусов вписанных и описанных
окружностей и вывод этих формул
2.Решить задачу:
Высота равнобедренного треугольника, опущенного на
основание, равна 9, а радиус вписанной в треугольник
окружности равен 4. Найдите радиус окружности,
касающейся стороны треугольника и продолжений
двух других его сторон.
13.
РефлексияНа рабочих листах допишите продолжение
следующих предложений:
1. Я научился...
2. Я могу научить других...
3. Я не понял / не смог...
4. В дальнейшем я …









 Математика
Математика








